建筑与数学

孙伟刚

早在19世纪，建筑中的数学已经进入了人们的视野. 建筑需要美，美源于和谐，和谐要用数学来创造. 20世纪瑞士著名建筑师勒·柯布西耶说：“几何形体用几何满足我们的双眼，用数学满足我们的理解.”

1. 胞体几何在建筑中的应用

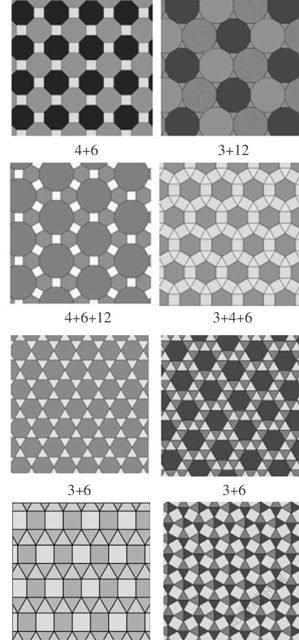
胞体几何原理：①能够无间隙拼连的单一的正多边形只有三种：正三角形、正方形、正六边形（如图1）.

②通过“拉伸”或“压扁”，等腰三角形、长方形、扁六边形，也能以单一个体无间隙镶嵌（如图2）.

③用不同的正多边形来拼铺整个平面，但每一个交叉点周围的正多边形种类和顺序都相同，叫做半正镶嵌图. 半正镶嵌图有8种（如图3）.

应用举例：“水立方”（奥运游泳馆）表皮 Skin尽管每个元泡形状不同，但交点都是三条边相交的“Y”形（如图4）.

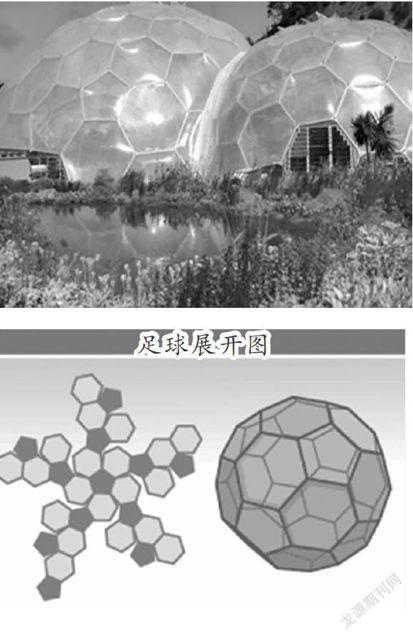
又如：美国伟大的设计学家巴克敏斯特·富勒（1895-1983）是第一个运用六边形和五边形构成的球形薄壳建筑结构，做成能源耗费极低，强度却很大的建筑物，后来这种结构被广泛运用，现代运动的足球，就是运用这个结构所制造（如图5）.

2. 拓扑几何在建筑中的应用

拓扑几何原理：一个几何图形任意“拉扯”（就像画在橡皮上），只要不发生割裂和粘接，可做任意变形，称为“拓扑变形”. 两个图形通过“拓扑变形”可以变得相同，则称这两个图形是“拓扑同构”. 如图6中，前三张图属于拓扑同构，但第（4）张图与前三张不同构.

拓扑几何就是研究几何图形在一对一连续变换中的不变的性质，而不考虑几何图形的尺寸、面积、体积等度量性质和具体形状的改变.

应用举例：欧美小住宅和中国四合院的拓扑结构不同，前者与球同构，后者与轮胎同构（如图7）.

又如德国数学家莫比乌斯（1790-1868）在1858年发现了拓扑的经典——莫比乌斯曲面，他将一个长方形纸条的一端固定，另一端扭转半周后，把两端黏合在一起 ，得到的曲面就是莫比乌斯带（如图8）. 像 2010年世博会丹麦馆（如图9）的造型就是莫比乌斯带. 哈萨克斯坦新国家图书馆（如图10）也是以莫比乌斯圈的形式将圆形、环形、拱形和圆顶形融合在了一起.

3. 克莱因瓶在建筑中的应用

克莱因瓶原理：一个瓶子底部有一个洞，现在延长瓶子的颈部，并且扭曲地进入瓶子内部，然后和底部的洞相连接. 三维空间中的克莱因瓶（如图11），没有“内部”和“外部”之分，它是由德国数学家菲利克斯·克莱因（1849-1925）首先提出的. 这个物体没有“边”，它的表面不会终结. 一只爬在“瓶外”的蚂蚁，可以轻松地通过瓶颈而爬到“瓶内”去.

应用举例：克莱因瓶别墅（如图12），是一栋位于澳大利亚摩林顿半岛的别墅. 这栋海滨别墅由澳大利亚McBride Charles Ryan建筑师事务所设计，曾获2009年度世界建筑节“最佳住宅”提名奖.

又如中国2010年上海世博会委内瑞拉国家馆（如图13）外观如“莫比斯环”，其三维立体结构被称为“克莱因瓶”，意为一个没有边界的、连续的闭合曲面；外部与内部相融会，比喻城市如同一条不间断的道路. 馆内的露天庭院、上升台阶、传统的土著居民生活空间、开阔的玻利瓦尔广场等极具民族特色的元素相互融合，展示委内瑞拉的文化、艺术和生活.

在古希腊和文艺复兴时期，建筑师往往都是数学家，如君士坦丁堡（今伊斯坦布尔）的圣索菲亚大教堂是由两位小亚细亚数学家伊西多鲁洛斯和安泰缪斯负责设计的，而剑桥大学三一学院图书馆则是由英国数学家雷恩设计的.

如今，建筑师与数学家集于一身的情形已不多见，但并不意味着建筑与数学分道扬镳，驻足欣赏北京水立方的华丽、国家大剧院的惊艳、上海体育馆的飘逸等等，我们分明在享受建筑中的数学之美.

（作者单位：江苏省无锡市港下中学）