数形结合法在高中数学教学中的应用研究
2015-09-10陈艳辉
陈艳辉


摘 要: “数形结合”是一种贯穿于高中数学教学中的数学思想与方法,注重数与形的相互转换.在高中数学教学过程中,运用数形结合思想方法,能够帮助学生更好更快地解决数学难题.“数形结合”通过用几何的形式诠释代数问题,从而体现出数学思维的美感.
关键词: 数形结合 高中数学 教学应用
高中数学教学是学生学习数学的重要阶段,学生的很多数学知识都是在高中的最终阶段真正掌握的,和初中数学相比较,高中数学更注重思维的灵活性.有效运用图形结合的数学方法,能够使问题简单化,提高解题效率.
一、数形结合的原则
(一)等价原则
等价原则指的是数学中的数与形在进行相互转换的过程中,应该是等价的.因为在数学中图形具有一定的局限性,所以我们在画图的时候,很容易出现所画图形不准确的问题,这样会严重影响解题效果因此,在运用数形结合解题的过程中,一定要遵循等价原则.
(二)双向原则
数形结合中的双向性原则指的是在对几何图形进行直观分析的同时,还要对它的代数性进行分析。由于代数的逻辑性和精确性相当高,因此双向性原则的运用可以直接减少几何的约束性,充分利用数形结合的优势.
二、数形结合在数学中的应用领域
(一)利用数形结合的方法解决集合问题
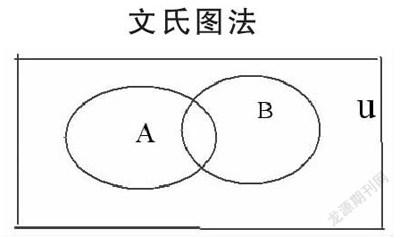
集合问题是高中数学中最基础的数学问题,对于集合问题的解决,能够有效帮助我们解决函数的取值范围问题,数形结合法恰能够有效解决集合问题.对于集合问题的解决,主要包括文氏图法与数轴解决法.下面笔者以文氏图法为例进行讲解.
例如:某比赛分为A、B两个项目,共有40人参加比赛,有15人参加了A项目,30人参加了B项目,问既参加了A项目,又参加了B项目的人数有多少个?
分析:这是一道十分简单的数形结合题,可以采取一种常见的数形结合的方式,即文氏图法,以下为运用文氏图法进行解题的方式.
文氏图法
设A={参加A项目的选手},B={参加B项目的选手},同时参加了两项目的人为x人,则通过文氏图分析可知,Card(A∩B)=5,那么x=5,则说明既参加A项目又参加B项目的有5人.
(二)利用数形结合法解决函数问题
在遇到函数的取值范围等题目时,很多学生都不知道该怎样并进行有效的解决.利用数形结合的方式解决函数值域的问题,不仅可以将复杂的数字简单化,而且可以在很大程度上提高解题效率,使数学函数问题变得更为简单.
例如:求函数y=|x-1|+|x+2|的值域.
分析:可以将函数y=|x-1|+|x+2|看成数轴上点P(x)到定点A(1),B(-2)的距离之和.所以,根据它的几何意义,可以采用数形结合的方式解题.
解:可以将函数y=|x-1|+|x+2|看成数轴上点P(x)到定点A(1),B(-2)的距离之和.由以下图形可知,当点P(x)在AB线段上时,y=|x-1|+|x+2|=|AB|=3;当点P(x)在线段AB的延长线或反向延长线上时,y=|x-1|+|x+2|>|AB|=3,所以通过分析可知,函数y=|x-1|+|x+2|的值域为[3,+∞].
(三)利用数形结合法解决几何问题
在利用数形结合法解决几何问题的过程中,主要有两种方式,一种是利用代数方法解决几何问题,另一种是利用几何方法解决代数问题,即我们通常所说的“数解形”及“以形解数”的解题方法,“以形解数”法通常被称为直观法或几何法.一般来说,所有的集合问题都可以运用代数的方法解决.例如:老师在教学过程中,可以通过提出题目,让学生发散思维,进行理解.例如:在利用代数解决几何问题时,要突出数形结合的思想,从曲线与方程的关系,点的轨迹方程的建立,几种常见曲线方程的建立等着手,充分进行数与形的转换.在集合问题的解决中,我们要充分认识到坐标系这个奇妙的工具,注意几何图形与代数知识之间的联系.
例如:设x>0,y>0,z>0,求证:,原命题转化成了AB+BC>CA,这显然是成立的.
三、数形结合有效应用的作用
首先,数形集合的有效应用能够引导学生更好地进行初、高中数学知识的过渡与衔接.其次,合理有效的数形结合数学方法的应用,能够培养学生独立思考的能力,将数与形相结合,能够使复杂的东西简单化,增强学生的数学学习信心.例如:通过数形结合的方式为代数问题提供集合模型,这样便能够更形象与直观地解释问题的本质.最后,数形结合的数学方法能够帮助学生多角度、多层次地思考问题,将动态思维与静态思维、抽象思维与形象思维进行完美结合.
总而言之,在高中数学教学过程中,数形结合的数学解题方式是一种十分合适的解题方式,学生领会了这一思想,对于学生提高解题效率、掌握数学知识具有重要的意义.
参考文献:
[1]杨平荣.对数形结合思想在初中函数教学中的作用探讨[J].学周刊,2015(22):144-145.
[2]马鸣.利用“数形结合”巧解初等数学问题[J].读与写(教育教学刊),2014(01):104-105.
