数学中考中几种问题的解决策略

盛爱霞

摘 要： 中考数学中有几个方面的问题学生丢分严重，课堂教学中需专题化解决.本文对存在性问题，数学建模问题，归纳、猜想型问题，动态问题等方面作探讨。

关键词： 数学中考 数学问题 解决策略

一、“存在性问题”解题策略

存在性问题是根据已知条件，探索制定适合某个问题的结论的数值、点、直线或其图形是否存在的题目，常见类型有：（1）等腰三角形存在问题；（2）直角三角形存在问题；（3）平行四边形存在问题；（4）相似三角形存在问题.在中考中，函数图像中点的存在问题是重点，其解题思路是：先对结论作出肯定的假设；然后由肯定假设出发，结合已知条件进行正确的计算、推理，若导出矛盾，则否定先前假设；若推出合理的结论，则说明假设正确，由此得出问题的结论.它主要考查考生的观察、分析、比较、归纳、推理等方面的能力.由于这类题目的综合性极强，因此中考常以压轴题出现.几何与代数相结合的综合题涵盖初中阶段所学的代数与几何的重要知识点和多种数学思想方法，特别注意运用数形结合的思想方法沟通几何与代数知识之间的内在联系，运用通过数研究形与通过形研究数的解题策略，主要题型为：在坐标系中研究直线型图形、圆、函数图像，在直线型图形和圆中研究几何变量之间的函数关系，从问题的类型来看主要有探索性问题、存在性问题、开放性问题.

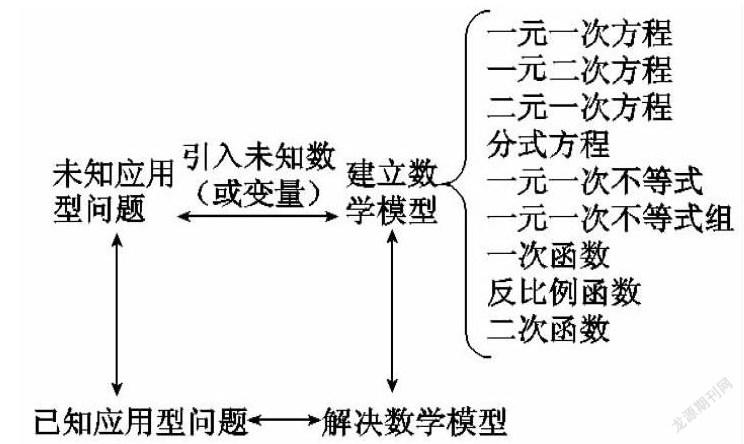
二、“数学建模问题”解题策略

数学应用性问题在近年的数学中考中是每一个省市必考的问题，这类问题的出题率越来越高，题材也越来越广泛.对这类有实用价值并且应用非常广泛的问题，通过数学建模的方法一般都可以抽象为数学应用题，因此探究运用建立数学模型的解题思路显得十分必要，在初中阶段通常建立方程模型、不等式模型、函数模型或几何模型.

三、“归纳、猜想型问题”解题策略

所谓归纳、猜想型问题指的是给出一组具有某种特定关系的数、式、图形或是给出与图形有关的操作、变化过程，要求通过观察、分析、推理、探求其中所蕴含的规律，进而归纳或猜想出一般性的结论，常见的类型有：（1）数式猜想型；（2）图形规律型；（3）数形结合猜想型.常结合的知识有：数与式的运算、因式分解、不等式的性质、平面直角坐标系、三角形、特殊四边形、几何变换图形的组合等.

解题思想方法：从考虑个别、特殊的对象出发，利用特殊性、特殊数量、特殊点、特殊线段、特殊位置等进行归纳、猜想、概括，从特殊到一般，从而得出规律.

四、“动态问题”解题策略

动态型问题是以点、线、面（如三角形、四边形）的运动为情境，探索和发现其中规律和结论的中考题型，由于图形的运动，导致题目的条件不断改变，随之相应的数量关系和结论也可能改变.这样就出现一个事件中蕴含着多个数学问题，既独立又有联系，使题目无论从考查知识上，还是解决方法上都具有较强的综合性，达到培养和考查学生的观察、试验、空间想象、分析综合等解决问题的能力的目的，在全国的中考试卷中常作为压轴题出现，类型有：（1）点的运动；（2）线的运动；（3）面（如三角形、四边形）的运动.

解决动态问题的思维与方法：（1）认清问题中的静态图形和动态图形，并确定动态图形的起始位置和终止位置；（2）画出不同时刻动态图形与静态图形形成的几何图形，这样就能由“动”变“静”，再设法分别求解问题.

例：如图，在平面直角坐标系中，抛物线y=ax+bx-3（a≠0）与x轴交于点A（-2，0），B（4，0）两点，与y轴交于点C.

（1）求抛物线的解析式；

（2）点P从点A出发，在线段AB上以每秒3个单位长度的速度向点B运动，同时点Q从点B出发，在线段BC上以每秒1个单位长度向点C运动.其中一个点到达终点时，另一个点也停止运动.当△PBQ存在时，求运动多少秒使△PBQ的面积最大，最大面积是多少？