复杂网络模型的动力学性质分析
2015-09-09赵雪茹
赵雪茹,丁 亮,牛 蕾
(东北林业大学)
0 引言
给出这样一个由N个相同节点构造成的具有连续时间耗散耦合星型网络系统,由于各节点在信息传输的过程中存在阻力、惯性等,就出现了一个时间滞后的现象,不妨假设这些内耦合函数都存在时间延迟τ,那么第i个节点的运动方程为:

1 星型网络模型的动力学性质研究
当τ=0时,第i个节点的运动方程为:

在条件R1:N∈Z+,N≥1;a>0;η>0下,特征方程为

下面进行零解稳定性探究.
对于方程(1):

方程(2)有N重根:λ3=-a-η.
定理1.1 在条件R1下:当时,那么系统的零解是渐近稳定的.
证明 对于方程(1)要使方程具有两个严格负实数的根,则有:

最后可得当η>0,对任意的a>,方程(1)的λ1,2<0,当η>0,如果对任意的0,那么λ1和λ2中至少有一个大于0.对于方程(2),要使得λ3<0,得a>-η,即a>0,根据时滞微分方程的稳定性理论可知,系统零解渐近稳定的充分必要条件是,方程(1)和方程(2)的所有根都有负实部,联立求解方程组,结论得证.
2 复杂网络模型的Hopf分支分析
由于各节点在信息传输的过程中存在阻力、惯性等,就出现了一个时间滞后的现象,而且这种时滞行为本身会影响到系统的现状,设这种延迟都为τ>0,得到延迟网络模型的运动方程为:

延迟模型的特征方程为:

其中:τ≥0;N∈Z+,N≥1;a>0;η≠0(H1)对于方程(3),在条件H1下,从方程可得:

当τ>0时,令λ=iβ(β>0)是方程(4)的纯虚根,则:
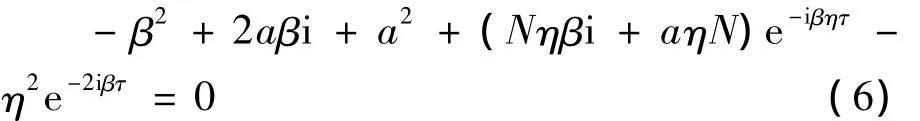

可得到β满足方程:β8+q1β6+q2β4+q3β2+q4=0
其中 ,q1=4a2-N2η2,q2=6a4-2η4-3N2η2a2- 2N2η4

那么β2是四次方程的正根.

引理2.1 若方程(8)有一个正根β2i(βi>0),则当β=βi时,方程(7)有实根因此当

其中

方程(4)有一对纯虚根±iβn.
引理 2.2 方程(4)在τ=τj=领域内有一对复根λ(τ)=α(τ)±iβ(τ)存在且Z,当L(β,τ)<0,因此在τ=τj穿过虚轴,发生hopf分支.
对方程(5)进行分析,解得

定理2.1 在条件H1下,且|η|>a,当τ=τ1时,方程(10)有一对纯虚根λ=±iβ1其中

证明 假设iβ1(βi>0)是方程(6)的解,通过分离实部和虚部,得
令λ(τ)=α(τ)+iβ(τ)满足α(τ1)=0,β(τ1)=β1是方程(10)的根,且有τ1=
定理2.2 在条件H1下,有

证明 将λ(τ)=α(τ)+iβ(τ)代入方程(10),对τ求导得
将λ=±iβ1代入上述方程,并将β1和τ1替换β和τ,则有
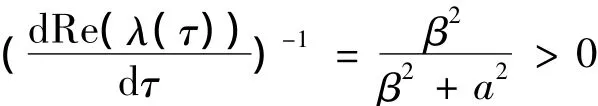
结论得证.
定理2.3 设N∈Z+,N≥1;a>0;η≠0,且|η|>a,且τ*由式(9)给出,τ1由式(11)给出,记τs=min{τ*,τ1},则当τ∈[0,τs)模型的零解渐近稳定的,当τ=τs,系统产生小振幅的周期解,当τ>τs时,复杂网络模型系统零解是不稳定的.
3 复杂网络模型数值仿真
在这一节里通过运用Matlab对星型网络模型进行数值仿真,通过数据和图像来验证其动力学性质.
(1)当N=4,a=1,η=3时,通过求解计算比较最后取得τs=0.6755,取初值[0,- 1,2,1,- 2]',其结果如图1、图2所示.

图1 τs=0.1系统的零解稳定图像
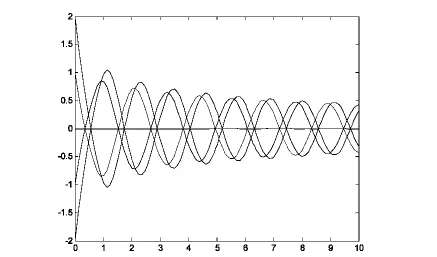
图2 系τs=0.6755统产生周期解的图像
(2)当N=2,a=2,η=3.5时,最后取得τs=0.9104,初值为[0.1.-1]',其结果如图3、图4所示.

图3 τs=0.002时系统的零解稳定图像

图4 系统产生周期解的图像
(3)取N=4,a=2,η=4 时,得τs=0.5895,取初值[0,0.1,-0.1,0.2,-0.2]'结果如图5、图6所示.
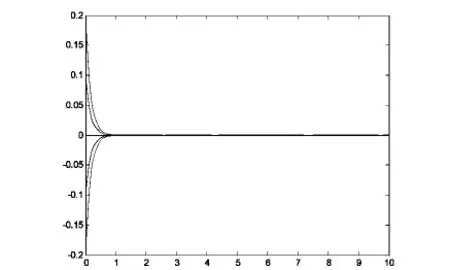
图5 τs=0.04时系统的零解稳定图像

图6 τs=0.5895时系统周期解的图像
[1]马佩杰.集群运动的同步及其在行人流中的应用[D].合肥:中国科学技术大学,2001.
[2]魏骏杰,王洪滨,蒋卫华.时滞微分方程的分支理论及应用[M].北京:科学出版社,2012.
[3]陆启韶,彭临平,杨卓琴.常微分方程与动力系统[M].北京:北京航空航天大学出版社,2010.
[4]梅凤祥,吴惠彬.微分方程的分析力学方法[M].北京:科学出版社,2012.
[5]周义仓,秦军林.常微分方程及其应用[M].北京:科学出版社,2003.
[6]陈姗姗.时滞导致反应扩散系统的不稳定性和Hopf分支[D].哈尔滨:哈尔滨工业大学,2010.
[7]钟益林,彭乐群,刘炳文.MATLAB求解[M].北京:清华大学出版社,2007.
[8]张家庄.非线性动力系统的运动稳定性、分叉理论及其应用[M].西安:西安交通大学出版社,2010.
[9]Sarika Jalan,Amritkar R F.Self- organized and driven phase synchronization in coupled maps[M].2003.
[10]孟宪章,魏俊杰.Stability and bifurcation of mutual system with time delay[M].2003.
[11]贺小明,彭明书.常微分方程与动力系统概论[M].北京:北京理工大学出版社,2010.
