双Jaynes-Cummings耦合模型中实现量子隐形传态的研究

帕肉克·帕尔哈提， 艾合买提·阿不力孜， 麦麦提依明·吐孙， 王 飞

（新疆师范大学物理与电子工程学院，新疆乌鲁木齐830054）

双Jaynes-Cummings耦合模型中实现量子隐形传态的研究

帕肉克·帕尔哈提， 艾合买提·阿不力孜∗， 麦麦提依明·吐孙， 王 飞

（新疆师范大学物理与电子工程学院，新疆乌鲁木齐830054）

利用双J-C耦合模型中两个二能级原子的纠缠态作为量子隐形传态的信道，研究了该模型中量子隐形传态的实现。详细讨论两原子处于W态时的纯度、两原子间初始纠缠度及光子数等系统参量对量子隐形传态保真度的影响。计算结果表明，通过提高初始态的纯度及纠缠度可以提高平均保真度，并且此时总可以实现量子隐形传态。另外还发现，光子数直接影响平均保真度演化过程中的频率和振荡衰减。

量子光学；Jaynes-Cummings模型；量子隐形传态；保真度

量子纠缠长期以来被认为是进行量子信息处理和量子计算的核心资源，尤其是在量子信息和量子通信处理过程中很重要的一个概念，比如在量子隐形传态［1］，量子稠密编码［2］和量子密钥分配［3］等方面。量子隐形传态是借助于量子纠缠态得以实现，是一种非常吸引人的非经典效应，最早Bennett提出了量子隐形传态协议［1］。在文献［4］中也应用此协议实现了量子隐形传态，其基本思想是［4，5］：通信双方借助于一对共享的纠缠态，一方可以把一个未知量子态以高于任何经典通信保真度的形式传送给遥远的另一方。发送者（假设为A1ice）对她手中的粒子和待传送的未知量子态进行联合Be11测量，然后把测量结果通过经典信道告诉接受者（假设为Bob）。当Bob接收到这个结果后，他对自己手中的粒子进行一次合适的转动操作，这样Bob就可以成功地得到A1ice要发送给他的未知量子态。量子隐形传态可以利用两个分隔两地的纠缠粒子和局域操作将未知量子态以优于任何经典协议的保真度传送给接收者，此方案先后在光子比特［6，7］和原子比特［8，9］中实现。

在量子信息和量子通信处理中，Jaynes-Cummings模型［10］是描述光场与原子相互作用的最简单和最典型的模型。至今，人们已利用J-C模型对光场与原子相互作用系统的量子特性作出了大量的研究［11-16］。为了描述量子信息领域中信息在传输过程中保持原有状态的程度，人们引入了保真度的概念。近年来，人们已对量子态保真度作了广泛的讨论，尤其是在利用其它推广的Jaynes-Cummings模型［17-20］。在J-C模型的基础上，附加外磁场、大失谐或频率变化场等情况下研究保真度的变化，但至今尚未见到在双Jaynes-Cummings耦合模型中实现量子隐形传态的研究。文章考虑两个分别处于各自光腔中的二能级原子作为研究对象，两原子的纠缠态作为量子隐形传态的信道，运用全量子理论并结合数值计算方法，讨论了被传送的原子初始纠缠度、原子态的纯度以及光子数对保真度的影响。给出了量子隐形传态信道容量的解析表达式，并讨论了该系统的各参量对量子隐形传态保真度的影响。

1 理论模型与密度矩阵

考虑把两个分别处于各自光腔中的原子作为研究对象。即假定有两个光腔a与b，a腔中有原子A，b腔中有原子B，两个腔之间及两原子之间都无相互作用，只考虑腔与各自腔内原子的耦合。则系统的哈密顿量可以写为［21］（ћ=1）

图1 系统模型

假定两原子处于Werner形态

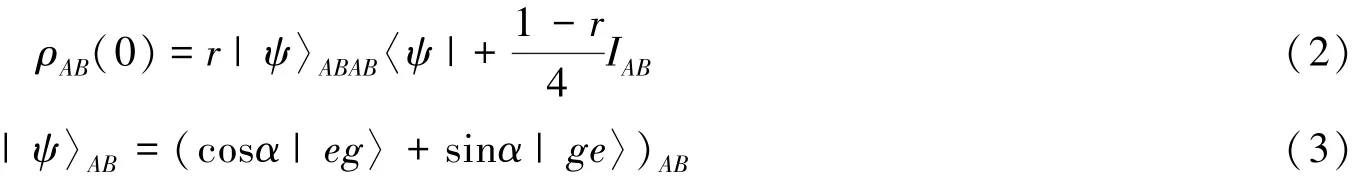
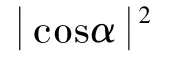
首先选择公式（2）中的态作为原子A，B的初态，并且假定腔中存在m，n≥0个光子数，|mn〉ab=|m〉a⊗|n〉b。这样，在t=0时刻整个系统的态为

而t时刻总系统的状态可写为

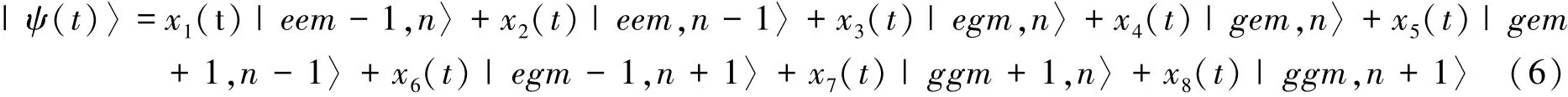
把式（1）和（6）代入薛定谔方程，并考虑初始条件x3（0）=cosα，x4（0）=sinα，x1（0）=x2（0）=x5（0）= x6（0）=x7（0）=x8（0）=0和共振条件Δ=ω-ν=0，求解上述方程组可得到

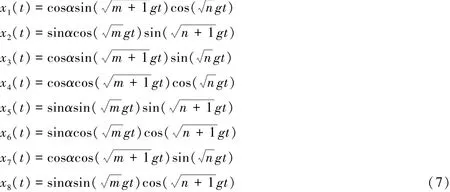
根据以上结果可以得出t时刻在基矢|ee〉，|eg〉，|ge〉，|gg〉下|ψ（t）〉AB对应的密度矩阵

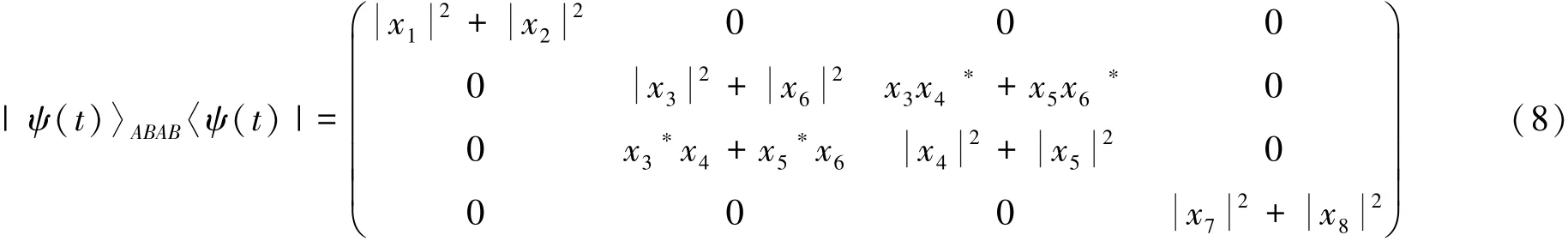
把（8）式代入（2）式可以得到系统的约化密度矩阵

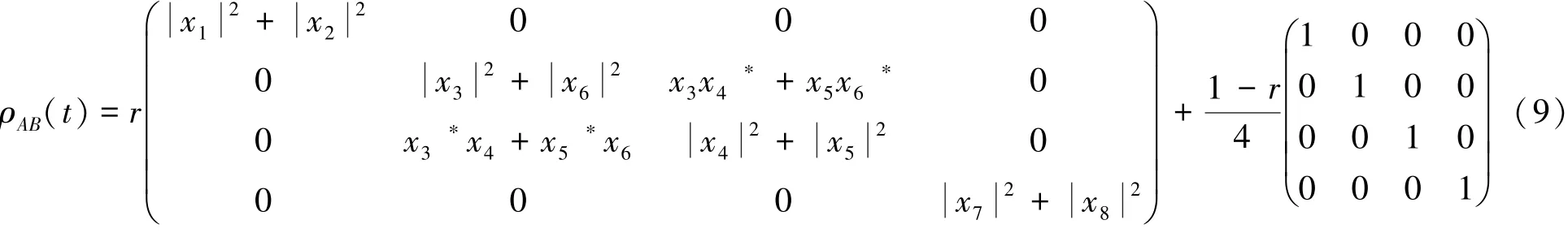
2 以两原子纠缠态为量子信道传送任意的单量子态

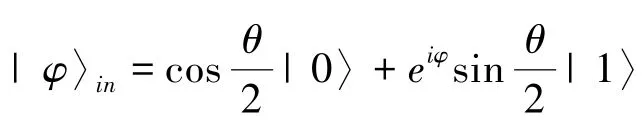
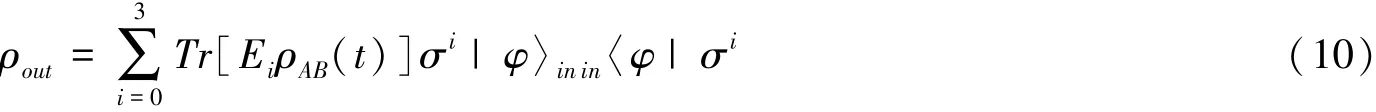
在量子隐形传态协议下，使用以上两个分别处于各自光腔中的原子纠缠态作为信道传递任意单粒子纯

态。被传输的任意未知单粒子纯态在布洛赫球上可表示为：

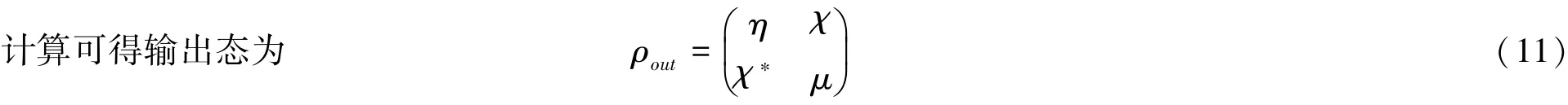
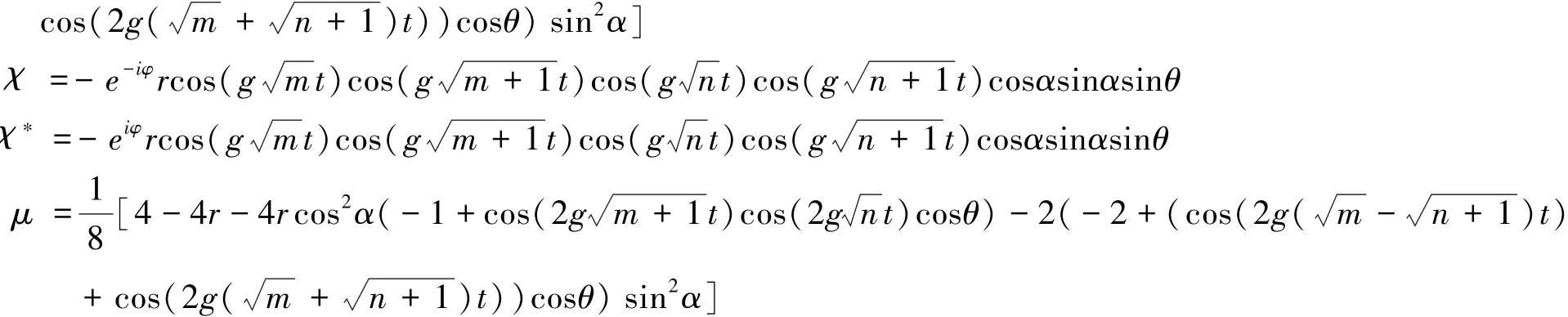
保真度描述量子隐形传态中信息丢失或是保存的多少，其定义为［23］

把（11）式代入（12）式通过计算，可以得到此时的保真度为

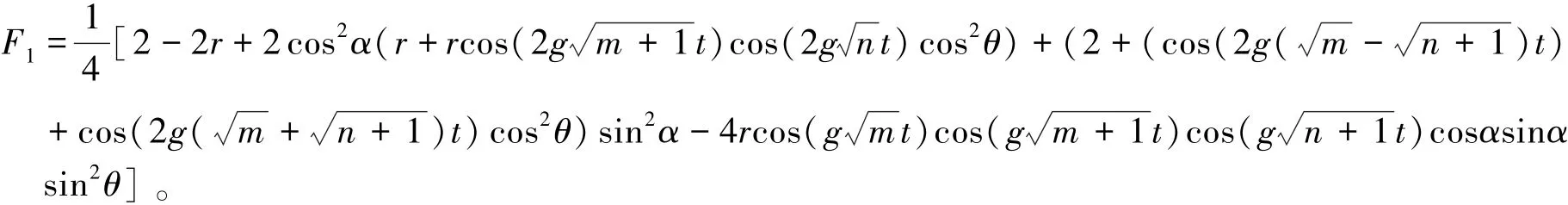
下标1表示传递单量子态的保真度。由于量子隐形传态的输入态是完全未知的，可以处于任意的可能态，所以计算包括所有可能被传输态的平均保真度更能准确地度量量子信息的传送质量

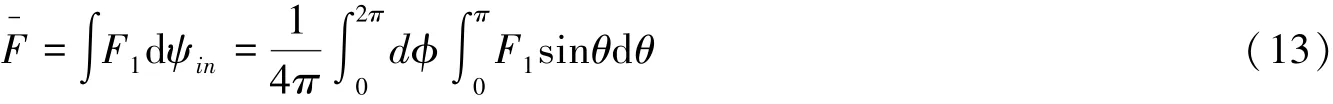
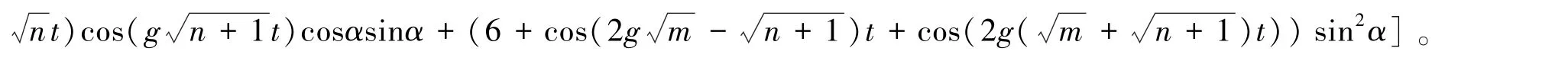
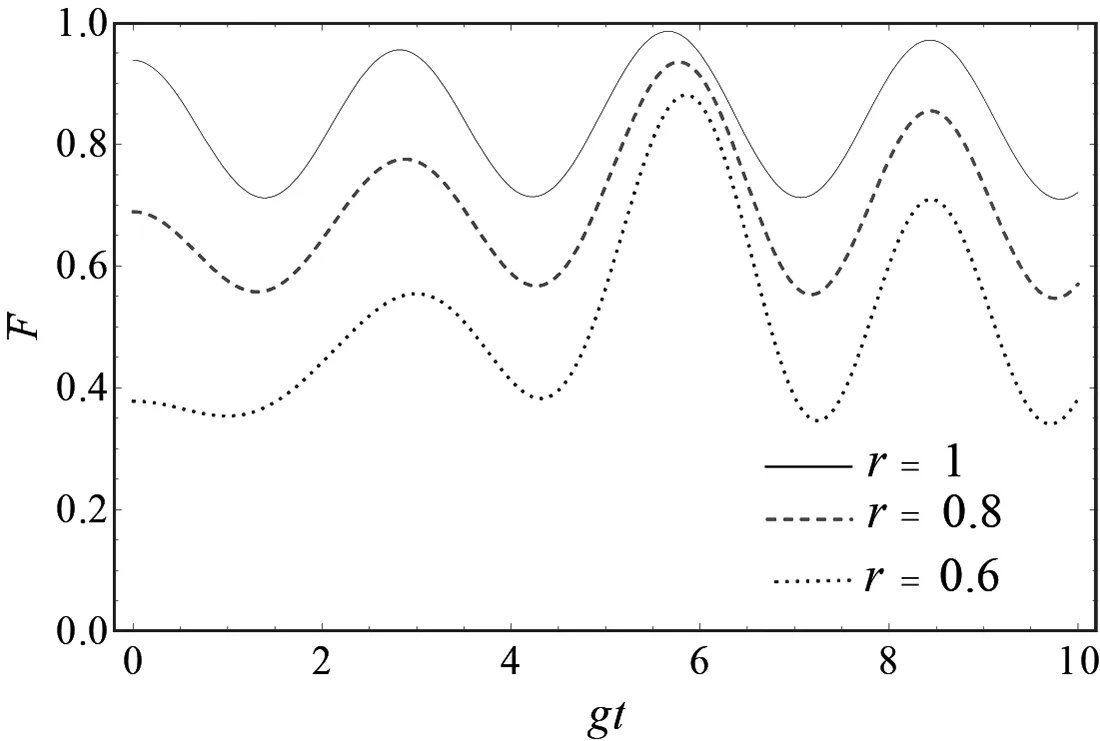
图2 初始态纯度不同时平均保真度的时间演化，参数取值为m=0，n=4，α=π/4

保真度是衡量量子隐形传态好坏的一个重要指标，图2是平均保真度在不同纯度下随时间的演化曲线。当其它参数固定而初始态纯度r逐渐提高时，平均保真度明显增大，即系统的纯度r直接影响了平均保真度的大小。此外，当r=1时在某些特殊时间点上平均保真度还可以达到最大值。当r=1时原子的初态约化为Be11型态，在文献［24］中，何敏等人提出了利用Be11态实现隐形传态的简单结构的量子线路，并且证明该量子线路是可行的。考虑提高平均保真度在以下的计算中均取r=1。

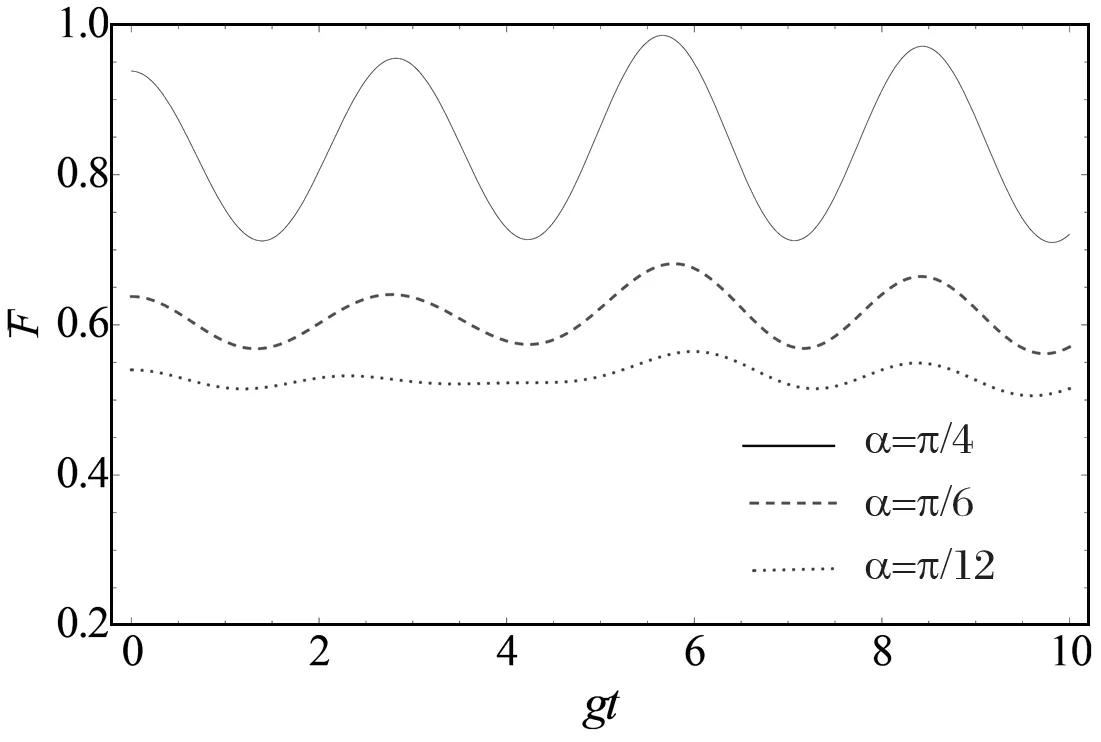
图3 a 平均保真度对不同初始纠缠度的时间演化，参数取值为r=1，m=0，n=4

图3 b 平均保真度随初始纠缠度和时间演化的三维图，参数取值为r=1，m=0，n=4

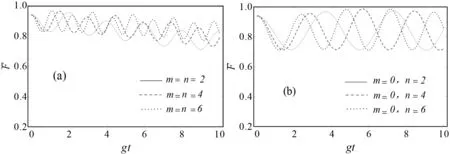
图4 光子数不同时平均保真度的时间演化，参数取值为r=1，α=π/4

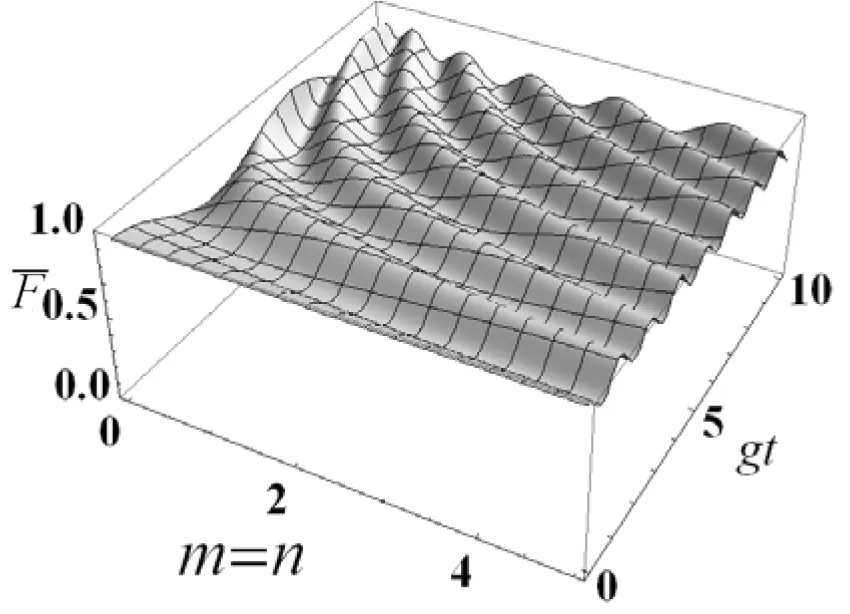
图5 平均保真度随光子数和时间演化的三维图，参数取值为r=1，α=π/4

3 结论

运用全量子理论研究了双J-C耦合模型两原子纠缠态作为量子隐形传态的信道，对输入态和纠缠通道受系统各参数的影响分别进行了研究，并对各种情况进行了数值计算。详细地讨论了信道容量随不同参数的变化关系。结果表明，通过提高两原子态的纯度，可以增大稠密编码的信道容量。两原子间初始纠缠度为最大纠缠态时，平均保真度在0.7-1之间周期性振荡，而且在特殊点能达到最大平均保真度值。最后，分别讨论了光子数m，n相等和不相等的情况，发现这两种情况下的平均保真度值有较大的差别。通过适当的参数组合用该模型总可以实现量子隐形传态。

［1］Bennett C H，Brassard G，Crepeau C，et a1.Te1eporting an unknown quantum state via dua1 c1assica1and Einstein-Podo1sky-Rosen channe1s［J］. Phys.Rev.Lett.，1993，70（13）：1895-1899.

［2］Bennett CH，Wiesner S J.Communication via one-and two-partic1e operators on Einstein-Podo1sky-Rosen states［J］.Phys.Rev.Lett.，1992，69（20）：2881-2884.

［3］Ekert A K.Quantum cryptography based on Be11＇s theorem［J］.Phys.Rev.Lett.，1991，67（6）：661-663.

［4］蔡江涛，艾合买提·阿不力孜.用三比特海森堡XXZ自旋环实现量子隐形传态［J］.新疆师范大学学报（自然科学版），2010，29（2）：20-24.

［5］蔡江涛.海森堡自旋链中的热纠缠及其在量子信息中的应用［D］.新疆师范大学硕士毕业论文，2010.

［6］乔盼盼，艾合买提·阿不力孜，蔡江涛等.利用热平衡态超导电荷量子比特实现量子隐形传态［J］.物理学报，2012，61（24）：514-518.

［7］Ursin R，Jennewein T，Aspe1meyer M，et a1.Communications：quantum te1eportation across the Danube［J］.Nature，2004，430（7002）：849

［8］Riebe M，Häffner H，Roos C F，et a1.Deterministic quantum te1eportation with atoms［J］.Nature，2004，429（6993）：734-737.

［9］Barrett M D，Chiaverini J，Schaetz T，et a1.Deterministic quantum te1eportation of atomic qubits［J］.Nature，2004，429：737

［10］Jaynes E T，Cummings FW.Comparison ofquantum and semic1assica1radiation theorieswith app1ication to thebeam maser［J］.Proc.IEEE.，1963，51（1）：89-109.

［11］李悦科，张桂明，高云峰.耦合双原子Jaynes-Cummings模型的腔场谱［J］.原子与分子物理学报，2004，21（4）：705-709.

［12］王菊霞.多模光场与二能级原子相互作用系统中保真度与纠缠度的关联［J］.光子学报，2014，43（3）：120-125.

［13］董传华.在克尔媒质中原子和光场的量子信息保真度［J］.光学学报，2003，23（10）：1181-1187.

［14］潘长宁，方见树，彭小芳等.耗散系统中实现原子态量子隐形传态的保真度［J］.物理学报，2011，60（9）：73-77.

［15］饶金同，王家驷，梁军.强度依赖Jaynes-Cummings模型中的量子态保真度［J］.激光技术，2012，36（5）：708-712.

［16］格日乐，萨楚尔夫，张彩花.玻色-爱因斯坦凝聚原子与Schrodinger猫态相互作用系统中的保真度［J］.原子与分子物理学报，2009：26.

［17］卢道明.频率变化场J-C模型中的量子态保真度［J］.光子学报，2010，39（2）：329-334.

［18］王菊霞.双原子与光场依赖强度耦合相互作用的保真度［J］.激光杂志，2012，33（6）：4-6.

［19］吕菁芬，马善钧.光子扣除（增加）压缩真空态与压缩猫态的保真度［J］.物理学报，2011，60（8）：11-17.

［20］王海军，高云峰，闫丽华.大失谐J-C模型中腔耗散对量子态保真度的影响［J］.原子与分子物理学报，2009，26（5）：882-886.

［21］Sainz I，Björk G.Entang1ement invariant for the doub1e Jaynes-Cummingsmode1［J］.Phys.Rev.A.，2007，76（4）：538-538.

［22］Bowen G，Bose S.Te1eportation as a depo1arizing quantum channe1，re1ative entropy，and c1assica1 capacity［J］.Phys.Rev.Lett.，2001，87（26）：367-376.

［23］Jozsa R.Fide1ity formixed quantum states［J］.J.Modern.Optics.，1994，41（12）：2315-2323.

［24］何敏，龚晶，姚泽清等.利用Be11态实现量子隐形传态［J］.通信技术，2007，40（12）：223-228.

Quantum Teleportation in the Double Jaynes-Cumm ings Coupling M odel

ParoukePAERHATl， Ahmad ABLlZ∗， Maimaitiyim ing TUSUN， WANG Fei
（College of Physics and Electronic Engineering，Xinjiang Normal University，Urumqi，Xinjiang，830054，China）

Using doub1e Jaynes-Cummings coup1ing mode1 in the two-1eve1 atomsof two entang1ed atoms as quantum te1eportation channe1，studied the rea1ization of quantum te1eportation.The effects of the initia1Werner-1ike state purity，initia1entang1ementand photon number on thefide1ity of quantum te1eportation are discussed.The resu1ts show that fide1ity can be increased by increasing the initia1purity and entang1ement and this time can a1ways rea1ization of quantum te1eportation.In addition a1so found，Fide1ity of average photon number direct1y affects the frequency and damping osci11ation in the process of evo1ution.

Quantum optics；Jaynes-Cummingsmode1；Quantum te1eportation；Fide1ity

O431.2

A

1008-9659（2015）04-059-06

2015-09-15

新疆维吾尔自治区杰出青年基金项目（2013911019）；国家高层次人才特殊支持计划后备人选之科技创新领军人才项目；自治区天山英才工程第二层次培养人选项目；新疆师范大学研究生科技创新项目基金资助（XSY201502001）。

帕肉克·帕尔哈提（1990-），男，新疆托克逊人，硕士研究生，主要从事量子信息与量子计算方向研究。

∗［通讯作者］艾合买提·阿不力孜（1974-），男，新疆轮台人，博士，教授，硕士生导师，主要从事量子信息与量子计算方向研究。