一类广义Sierpin'ski图的原子键连通度
2015-09-07辛玉忠梁晓东
辛玉忠, 梁晓东
(新疆大学数学与系统科学学院,新疆乌鲁木齐830046)
一类广义Sierpin'ski图的原子键连通度
辛玉忠, 梁晓东∗
(新疆大学数学与系统科学学院,新疆乌鲁木齐830046)
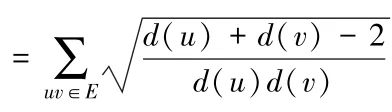
Sierpin'ski图;广义Sierpin'ski图;ABC指标
拓扑指标在化学,药理学等方面的研究中发挥着重要的作用。上世纪中叶以来,研究者们提出了各种各样的拓扑指标(参见[1,2000]),其中以1975年由MilanRandic′提出的Randic′指标最具代表性[2]。1998年,Estrada等人提出了原子键连通度(ABC)指标[3]。一个图G的原子键连通度(ABC)指标定义为:

其中,d(u)表示点u在G中的度数。ABC指标在化学热力学及数学化学中均有广泛的研究[4]。
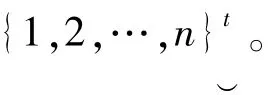
定义1 Sierpin'ski图S(kn,t)的顶点集是V(S(kn,t))={1,2,…,n}t。{u,v}是S(kn,t)的一条边,当且仅当存在i∈{1,2,…,t}使得:
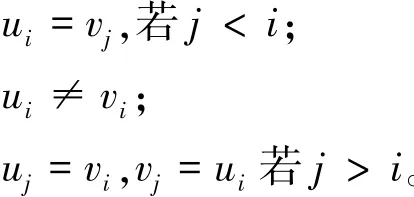
在文献[9]中,这个结构推广到了任意图G,定义为广义Sierpin'ski图,记作S(G,t)。
定义2 广义Sierpin'ski图S(G,t)的顶点集是V(S(G,t))={1,2,…,n}t。{u,v}是S(G,t)的一条边,当且仅当存在i∈{1,2,…,t},使得:
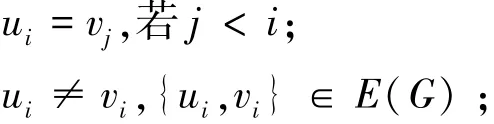
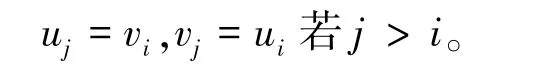
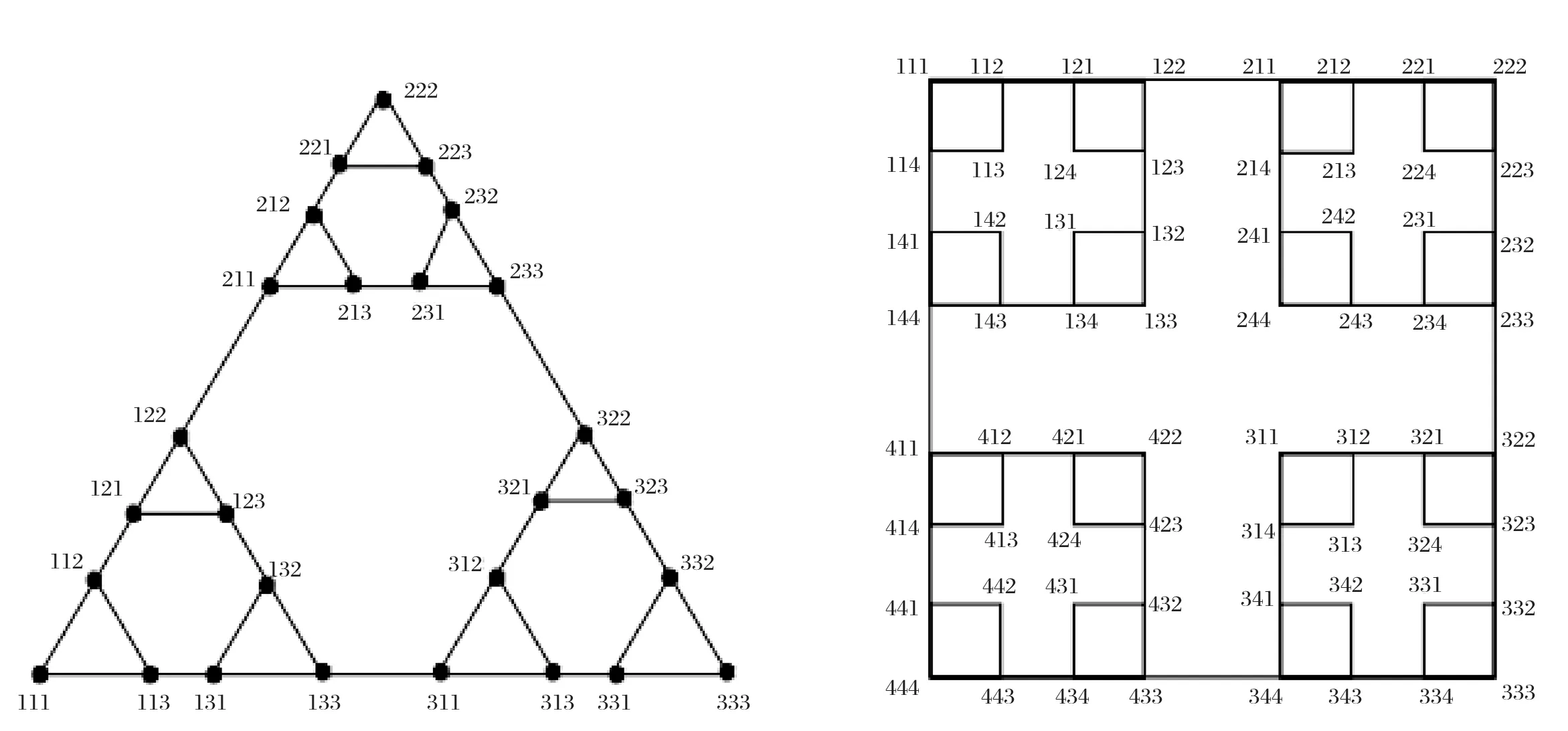
图1 Sierpin'ski图S(K3,3)和广义Sierpin'ski图S(C4,3)
注意到S(G,t)可以由G构造,步骤如下:当t=1时,S(G,1)=G。当t≥2时,首先将S(G,t-1)复制n次,然后在与x相应的那个S(G,t-1)的每个顶点标签之前添加x,对于G的每一条边{x,y},在点xyy…y和yxx…x之间添加一条边。标号为xx…x的点称为极点。对于任意n阶图G以及任意整数t≥2,S(G,t)有n个极点。若点x在G中的度数为d(x),则极点xx…x在S(G,t)中的度数也为d(x)。S(G,t)中的两点xyy…y和yxx…x连接S(G,t-1)的两个拷贝,故它们的度数分别为d(x)+1和d(y)+1。

图2 聚合物Sierpin'ski图P(K2,3)
用Pn表示阶为n的路。在文献[10,11,2003-2005]中,介绍了构造P(Kn,t)的方法。对于n阶连通图G,文献[12,2015,145-160]中给出了聚合物Sierpin'ski图P(G,t)的如下定义。
定义3 对任意i∈{1,2,…,t},定义集合Ai={ai1,ai2,…,aini-1}。记S(G,i)=(Vi,Ei),其中Vi={vi1,vi2,…,vini}。则广义Sierpin'ski图P(G,t)的点集和边集分别为:
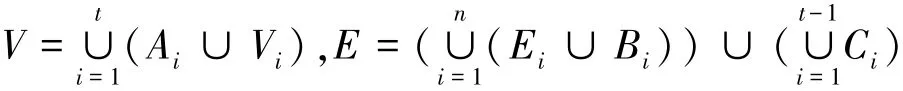
注意到,P(G,t)可以由如下步骤构造:当t=1时,P(G,1)是由a11连接S(G,1)的一个拷贝的每个顶点构成的。当t=2时,为了得到P(G,2),需要运用P(G,1),A2,S(G,2);把每一个a2j∈A2与v1j∈V1连接,并且把a2j与G在S(G,2)中的第j个拷贝的所有点连接。相似地,为了得到P(G,t),需要运用P(G,t-1),At,S(G,t);把每一个atj∈At与vt-1j∈Vt-1连接,并且把atj与G在S(G,t)中的第j个拷贝的所有点连接。
文章中考虑基于广义Sierpin'ski图的网络模型,获得了聚合物Sierpin'ski图P(G,t)的ABC指标的公式,其中G是一个完全图或一个无三角形δ正则图。
1 计算P(G, t)的原子键连通度
其中,
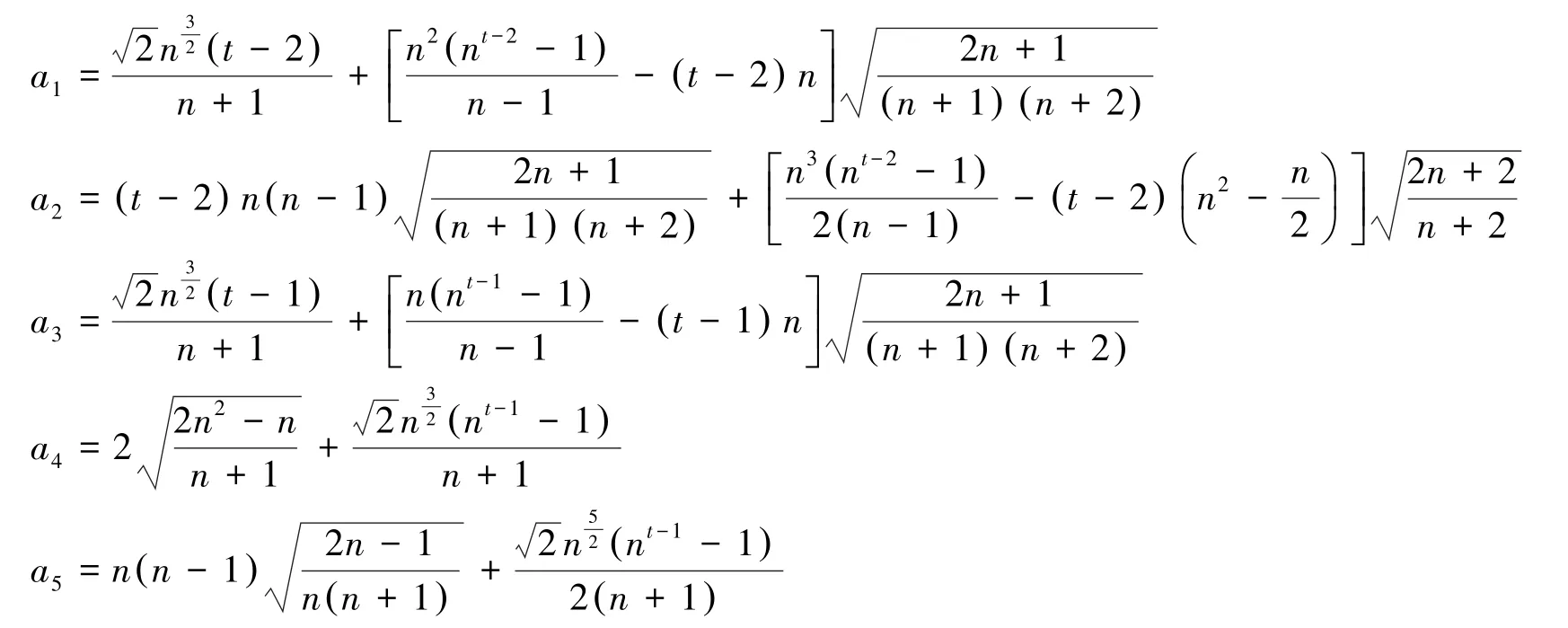
证明 令d(x)为点x在P(G, t)中的度数,对P(G, t)中的边 {x, y},分如下情况讨论:
(1)x=a1,y∈V1。这种情况下,P(Kn,t)有n条边 {x, y},其中d(x)=n,d(y)=n+1,这些边对ABC指标的贡献为:


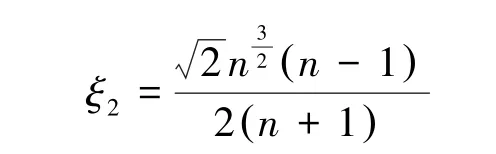
(3)x∈Ai,y∈Vi,2≤i≤t-1。P(Kn,t)有n条边 {x, y},其中y是S(Kn,i)的极点,d(x)=d(y)= n+1。同时有ni-n条边 {x, y},其中y不是S(Kn,i)的极点,d(x)=n+1,d(y)=n+2。这些边对ABC指标的贡献为:

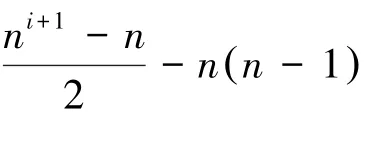

(5)x∈Vi,y∈Ai+1,1≤i≤t-1,P(Kn,t)n条边 {x, y},其中x是S(Kn,i)的极点d(x)=d(y)= n+1。同时有ni-n条边 {x, y},其中x不是S(Kn,i)的极点,d(x)=n+2,d(y)=n+1。这些边对ABC指标的贡献为

(6)x∈At,y∈Vt。P(Kn,t)有n条边{x,y},其中y是S(Kn,t)的极点,d(x)=n+1,d(y)=n。同时有nt-n条边{x,y},其中y不是S(Kn,t)的极点,d(x)=d(y)=n+1。这些边对ABC指标的贡献为:
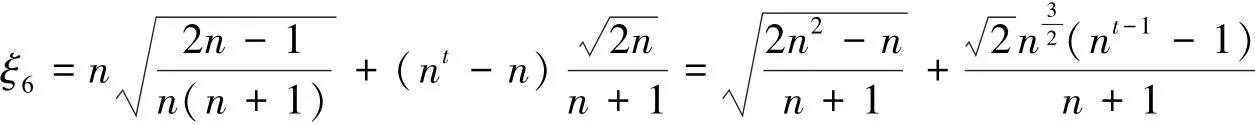
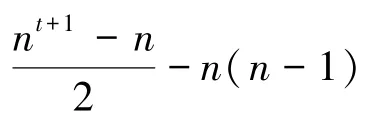

推论2 对任意阶为n≥2的δ正则图G,
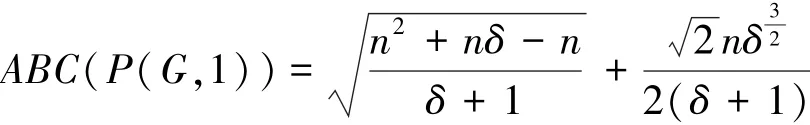
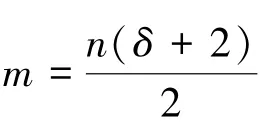
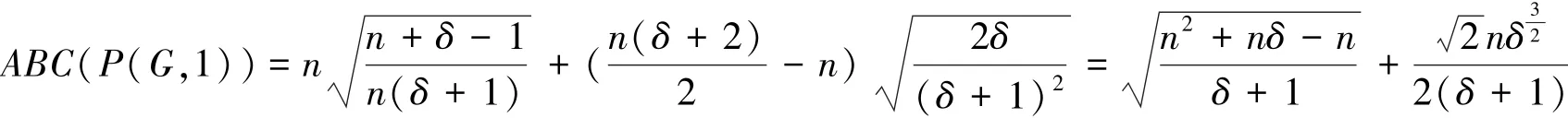
对给定的图H,用gH(δ)表示度数为δ的点的个数。
引理3[12]对于任意无三角形的n阶δ正则图G以及任意正整数t≥2,
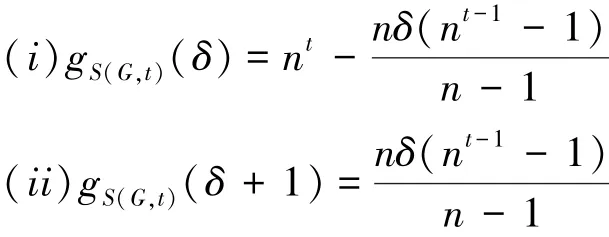
对给定的图H,用fH(δ,δ')表示两个顶点度数分别为δ和δ'的边的个数。
引理4[12]对于任意无三角形的n阶δ正则图G以及任意正整数t≥2,
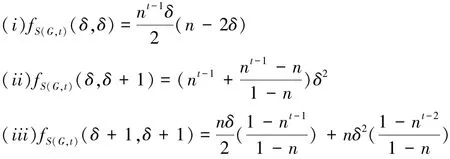
定理5 对于任意无三角形的n≥2阶δ正则图G以及任意整数t≥2,

其中,

证明 令d(x)为点x在P(G,t)中的度数,{x, y}为P(G,t)中的边。
(1)x=a11,y∈V1。这种情况下,P(G,t)有n条边 {x, y},其中d(x)=n,d(y)=δ+2。这些边对ABC指标的贡献为:
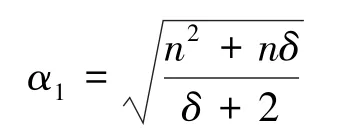
(2)x,y∈V1。 P(G,t)有条边 {x, y},其中d(x)=d(y)=δ+2。这些边对ABC指标的贡献为:
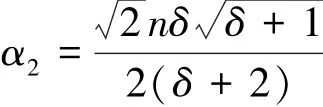
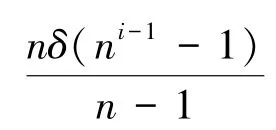
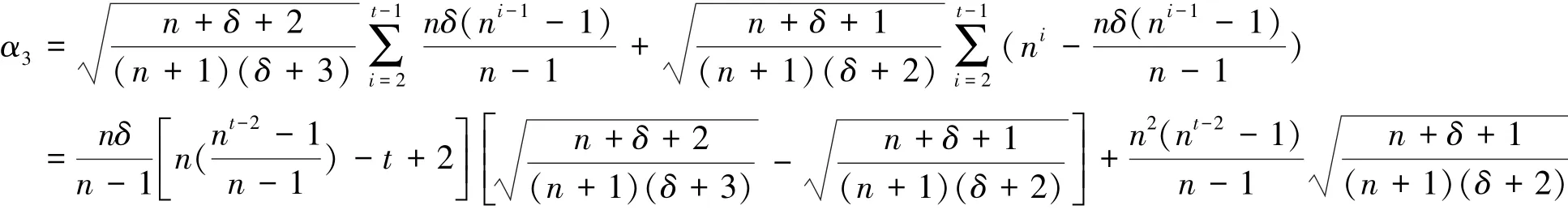
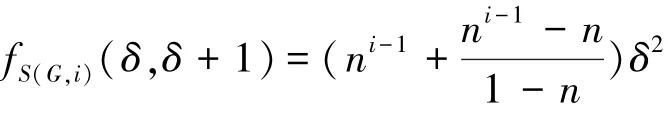
d(x)=d(y)=δ+3。 这些边对ABC指标的贡献为:



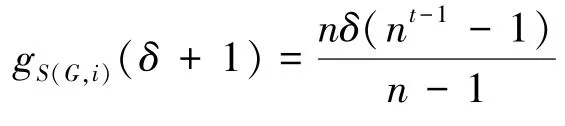

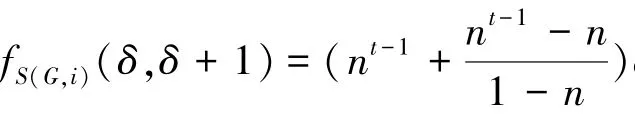

[1]R.Todeschini,V.Consonni.Handbook ofmo1ecu1ar descriptors[J].Wi1ey-VCH,Weinheim,2000.
[2]M.Randic′.On characterization ofmo1ecu1ar branching[J].Am.Chem.Soc,1975,(97):6609-6615.
[3]E.Estrada,L.Torres,L.Rodríguez,I.Gutman.An atom-bond connectivity index:mode11ing the entha1py of formation of a1kanes,Indian[J]. Chem.1998,(37A):849-855.
[4]E.Estrada,Atom-bond connectivity and the energetic of branched a1kanes[J].Chemica1Physics Letters,2008,(463):422-425.
[5]I.Gutman,J.Tosovic',S.radenkovic',S.Markovic',On atom-bond connectivity index and its chemica1app1icabi1ity[J].Indian Journa1of Chemistry,2012,(51A):690-694.
[6]A.Graovac,M.Ghorbani,A new version of the atom-bond connectivity index[J].Acta Chimica S1ovenica,2010,(57):609-612.
[7]X.Ke,Atom-bond connectivity index of benzenoid systems and f1uoranthene congeners[J].po1ycyc1ic Aromatic Compounds,2012,(32):27-35.[8]S.K1avzar,U.Mi1utinovic,Graphs S(n,k)and a variant of the tower of Hanoi prob1em,Czech[J].Math.J.1997,(47):95-104.
[9]S.Gravier,M.Kovse,A.Parreau,Genera1ized Sierpin'ski graphs[J].Des.Codes Cryptogr.2013(69):181-188.
[10]A.Jurjiu,Dynamics of po1ymer networksmode1ed by finite regu1ar fracta1s[J].Ph.thesis.Univ.Freiburg,2005.
[11]A.Jurjiu,T.Kos1owski,A.B1umen,Dynamics of deterministic fracta1po1ymer networks:hydrodynamic interactions and the absence of sca1ing[J]. Chem.Phys.,2003,(118):2398.
[12]Juan A.Rodriguez-Veazquez,Jessica Toma's-Andreu.On the randic′index of po1ymeric networksmode11ed by genera1ized Sierpin'ski graphs,MATCH Commun[J].Math.Comput.Chem,2015,(74):145-160.
Atom-bond Connectivity Index of Generalized Sierpin'ski Graph
XlNYu-zhong, LlANG Xiao-dong∗
(School ofMathematics and System Sciences,Xinjiang University,Urumqi,Xinjiang,830046,China)
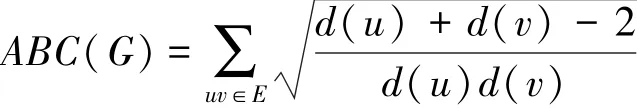
Sierpin'ski graph;Genera1ized Sierpin'ski graph;ABC index
O157.5
A
1008-9659(2015)04-031-07
2015-09-17
新疆维吾尔自治区重点实验室开放课题资助(2015KL019)。
辛玉忠(1991-),男,青海人,硕士研究生,主要从事图与网络优化方面的研究。
∗[通讯作者]梁晓东(1970-),男,副教授,博士,硕士生导师,主要从事图与网络优化方面的研究。
