基于卷积型正交条件的小波构造方法

张小燕， 吐尔洪江·阿布都克力木， 冯 惠， 热依木汗·热西提

（新疆师范大学数学科学学院，新疆乌鲁木齐830054）

基于卷积型正交条件的小波构造方法

张小燕， 吐尔洪江·阿布都克力木∗， 冯 惠， 热依木汗·热西提

（新疆师范大学数学科学学院，新疆乌鲁木齐830054）

文章通过采用卷积型正交条件提出了一种正交小波的构造方法。通过做这些得到的小波是包含Daubechies小波紧支撑特性的特殊小波。在一些受限制的条件下，通过改变小波中的自由参数来分析构造几个对称并且近乎紧支撑的小波。

紧支撑；卷积参数；线性相位；小波

1987年Ma11at提出的多分辨率分析是构造小波的一个非常重要的概念【1】。在多分辨率分析中，利用二尺度关系介绍了较光滑和较粗糙的函数空间，并且这个较光滑的尺度空间可以分解为一个较粗糙的空间和该粗糙空间的正交补集空间而小波是根据一个补充的空间构造的一个母函数。将多分辨率分析作为依据，1988年Daubchies设计了紧支撑正交小波滤波器【2】，从信号中提取优良的高频分量。然而，这些小波不具有线性相位，除了Haar小波之外【3】。在信号处理中，线性相位比正交性更加重要。设计具有线性相位小波函数的方法之一就是放宽正交性条件。Unser和A1droubi通过利用奇数阶的B—样条函数的二尺度关系已经构造出了双正交小波【4】。

文章构造的卷积型小波既不是从像B—样条函数这样的特殊小波衍生出来的，也不是对滤波器组概念的延拓。为了使新构造出的小波具有线性相位，故将自由参数放在一个满足正交条件的尺度函数中，通过做这些，可以得到一个包含有Daubechies紧支撑小波的离散小波正交类。新构造的小波和小波滤波器包含有更多的优点并且这些新构造的滤波器强调信号物理上的高频成分。

1 尺度函数正交条件

尺度函数φ（x）∈L2（R）且其满足二尺度关系：

其中Z为一切正数；αn为实参数。Daubechies发现φ（t）的平移族｛φ（·-k），k∈Z｝正交条件为

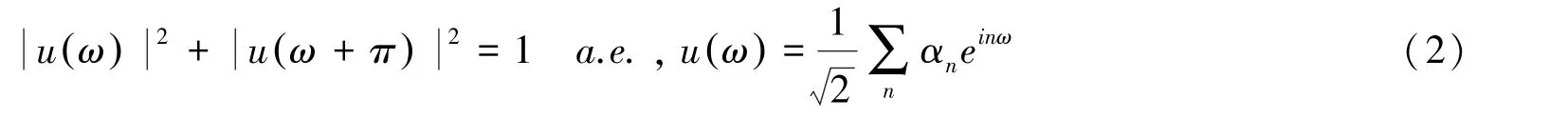
文章通过介绍一个函数φp（x）（φp（x）∈L2（R））满足二尺度关系：

其中p=（pm）m=-M，...M均为实参数；α=（αn）n∈Z为（1）式中出现的尺度系数；符号∗表示为卷积运算：

若p0=1且pm=0（m≠0）则φp（x）和φ（x）一致。

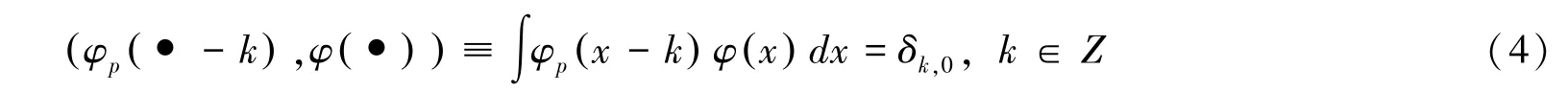
现在定义a（ω）以便以后使用：，下面的定理成立。

2 内积与规范尺度函数空间

设V0为平移尺度函数 ｛φ（· -k），k∈Z｝的扩张空间

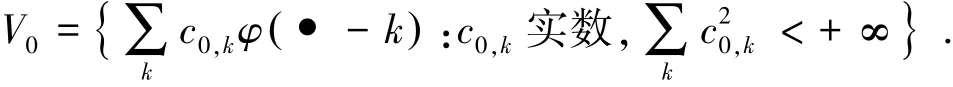
在尺度函数空间φ（x）上再定义一个更大的空间V1

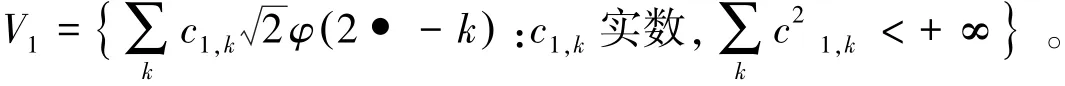
将f（x）中的系数ck由上述定义的参数p=（pm）代替。再定义一个函数fp（x）：

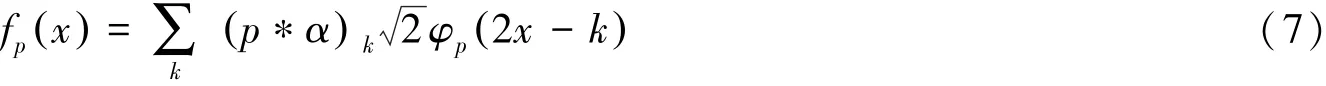
如果（7）中的cn与（1）式中的αn等价那么fp（x）与（3）式中的φp（x）等价。（f， g）p如下定义：

（f， g）p可以简写为 （f， g）p≡ （fp， g）

让参数p=（pm）满足如下两个假设条件：

H1）pm=p-m

H2）a（ω）＞0 a.e.

假设条件H2是为了满足以后构造小波函数的需要。对于任意的f∈V1都满足条件 （f，f）p≥0的充分条件就是a（ω）＞0 a.e.。

命题1 假设条件H1）和H2）均满足则有对于任意的f∈V1都满足 （f，f）p≥0。

在假设条件H1和H2下，可以得到以下的结果。

命题2 （8）式中的 （f， g）p是在空间V1中的一个内积计算并且‖f‖p= （f，f）p于空间V1成立。

3 小波

由命题2，空间 （V1，‖·‖p）变成一个Hi1bert空间。由（1）式可得V0⊂V1，V1可以被分解：

V1可以写成V0与W0直和的形式。W0空间在V1空间中被称为V0空间的正交补空间。在W0空间构建一个正交基形式为 ｛ψ（· -k），k∈Z｝，则ψ（x）被称为小波函数。W0空间也可以被写成：

由于V0⊥W0故小波ψ（x）必须的满足：（φ（· -k），ψ（·））p=0，k∈Z.根据内积的定义 （· ，·）p，可得因ψ∈W0⊂V1，故ψ（x）被扩展为

小波ψ（x）必须满足正交性条件即：（ψ（· -k），ψ（·））p=δ0k，k∈Z。很明显 ｛ψ（· -k），k∈Z｝

为W0空间中的一个正交基。为了找到（12）式中的小波，就必须对系数βn如下定义。

4 探究N=2和M=1的条件下的尺度函数与小波

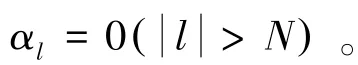
现在我们兴趣就在于当N=2和M=1时（13）式的解析解。假设N=2时尺度函数具有紧支集。假设长度为M=1和M=2时的两种可能性。卷积参数为p=（pm），为了简便选取条件M=1。当N=2和M=1时（13）式可以写成：

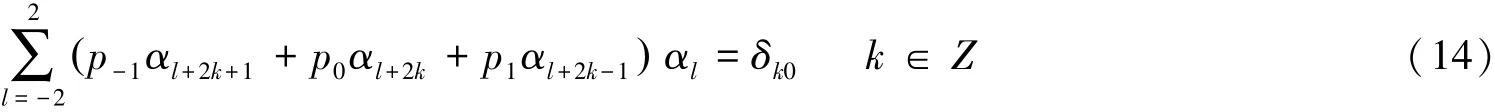
其中αn（n=0，±1，±2）均为未知系数。

由于方程（14）式中的k=1，2分别与k=-1，-2一致，故当k=-2，-1，0时，且满足条件p1=p-1时，可根据Daubechies滤波器构造方法可以得到以下方程：

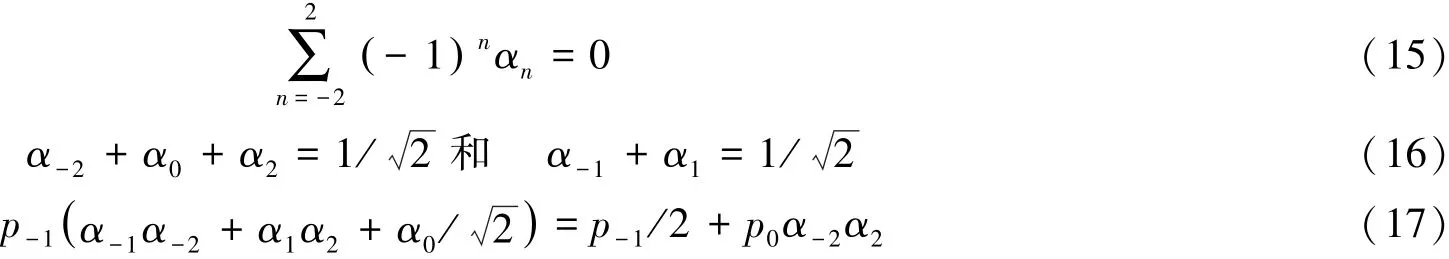
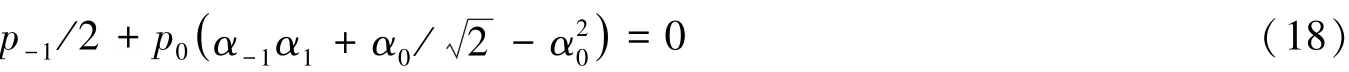
通过表1和表2可以分别利用q1，q2，s±和y±给出最终的结果，其中

表1 放缩系数1/2＜p0＜3- 5或者2＜p0≤3+ 5

表2 放缩系数3-5≤p0≤2

表3 放缩系数p0=3-5

表4 放缩系数p0=2

ⅰ）当1/2＜p0＜3- 5或者2＜p0≤3+ 5时，可以得到一对实数解。

ⅱ）当3- 5≤p0≤2时，可以得到两对实数解。

ⅲ）当p0≥3+ 5时，没有实数解。

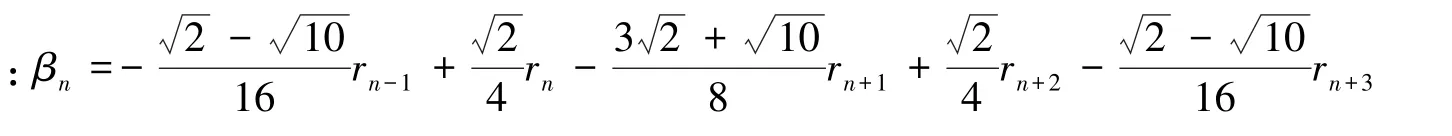
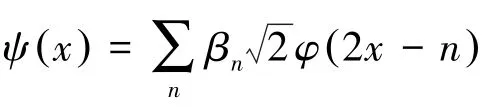
然而针对它们所对应的尺度函数和小波函数对称性的控制关系在图1、图2和图3中表示出来。

卷积型小波是Daubechies小波理论的延伸，是在N=2和M=1条件下通过调整卷积参数p=（pm），可以得到四对对称的并且具有线性相位的尺度函数和小波。

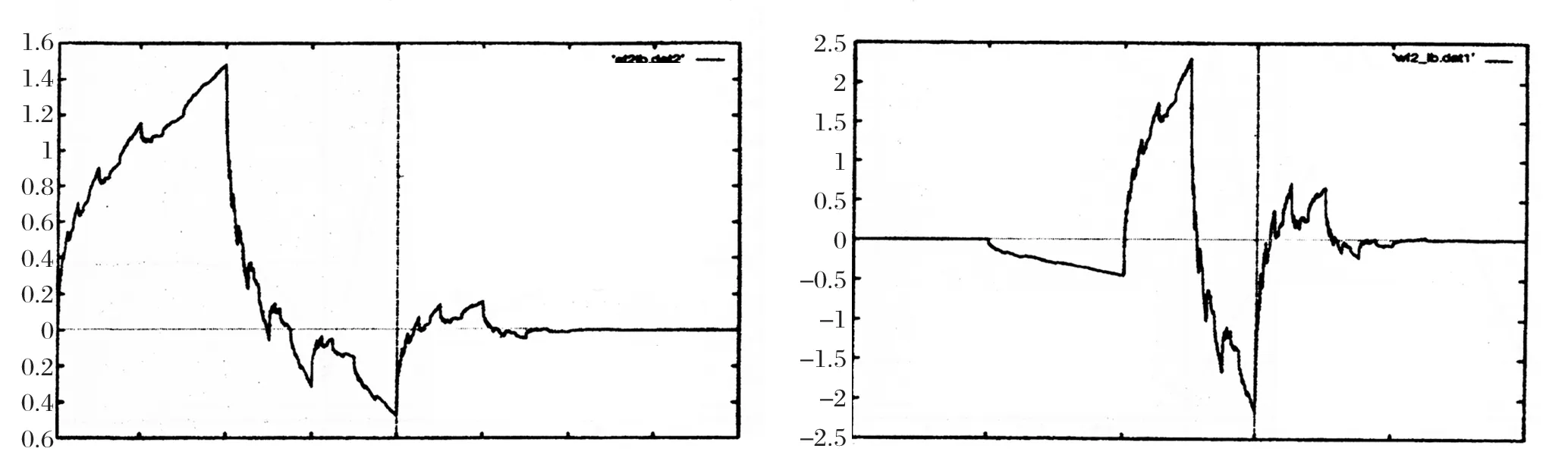
图1 尺度函数φ（x）和小波ψ（x）（p0=3-，p-1=p1=/2-1）

图2 尺度函数φ（x）和小波ψ（x）（p0=2，p-1=p1=-0.5）

图3 尺度函数φ（x）和小波ψ（x）（p0=3+，p-1=p1=/2-1）

［1］Stephane G.Ma11at，Mu1tireso1ution approximation and wave1etorthogona1bases in L2［J］.Transactionsof American Mathematica1Society，1989，315（1）：69-87.

［2］Ingrid.Daubechies，Orthonorma1bases of compact1y supported wave1ets［J］.Communications on Pure and App1ied Mathematics，1988，41（7）：909-996.

［3］Ten Lectures on Wave1ets［M］.Phi1ade1phia，PA：SIAM，1992：126-133.

［4］M.Unser and A.A1droubi，Po1ynomia1sp1inesand wave1ets-A signa1processing perspective［C］.Wave1ets--A Tutoria1in Theory and App1ications，C.K.Chui，Ed.New York：Academic，1992，20（8）：92-122.

［5］吐尔洪江·阿布都克力木.小波信号处理基础［M］.北京邮电大学出版社，2014：90-115.

［6］李广印，孙云平，贾纳豫.一类控制方向未知不确定性系统的自适应选代学习控制［J］.云南师范大学学报（自然科学版），2015，35（4）：19-27.

W avelet Construction M ethod Based on Convolution Type Orthogonal Condition

ZHANGXiao-yan， Turghunjan ABDUKlRlM TURKl∗， FENG Hui， Reyima RlXlT
（School ofMathematical Sciences，Xinjiang Normal University，Urumqi，Xinjiang，830054，China）

This paper proposes a new method for constructing orthogona1wave1etby using the orthogona1wave-1et transform.Such wave1et function contains the Daubechies'compact1y supported wave1ets as a specia1 case.In some restrained cases，severa1 symmetric and a1most compact1y supported wave1ets are constructed ana1ytica11y by tuning free convo1ution parameters contained in the wave1et function.

Compact support；Convo1ution parameter；Linear phase；Wave1et

O174.2

A

1008-9659（2015）04-047-08

2015-09-15

国家自然科学基金资助项目（11261061，61362039，10661010）；新疆维吾尔自治区自然科学基金资助项目（200721104）。［作者简介］张小燕（1991-），女，新疆石河子人，硕士研究生，主要从事小波分析及其应用方向的研究。

∗｛通讯作者｝吐尔洪江·阿布都克力木（1962-），男，新疆博乐人，博士，教授，主要从事小波分析及其应用方向的研究。