李冶数学教育思想对当代大学数学教育改革的启示
2015-09-06安宏伟郑莉芳张媛媛
安宏伟, 郑莉芳, 张媛媛, 彭 丽
(1.石家庄铁道大学四方学院,河北 石家庄 050043;2.石家庄学院,河北 石家庄 050035)
一、李冶的数学成就及对我国古代数学的重要贡献
李冶(1192—1279),字敬斋,金真定府栾城(今河北栾城)人,是金末元初著名的学者,中国数学史上宋元四大家之一,他总结并完善了天元术,编著了两部天元术著作——《测圆海镜》和《益古演段》,为我国古代数学发展做出了重要贡献。
《测圆海镜》是我国现存最早的一部以天元术为主要内容的著作。天元术是一种用数学符号列方程的方法。书中“立天元一为某某”相当于现在的:设x为某某。《测圆海镜》的成书对我国古代数学发展具有深远的影响。
(1)从内容上来说,《测圆海镜》是一部代数著作,它总结并提高了天元术,使方程理论基本上摆脱了几何思维的束缚,这是数学思想的重大突破。随着这一重大突破,李冶在方程理论上的研究有了很大的进展,明显提高了方程的一般化程度。李冶在《测圆海镜》中改变了传统的把“实”(指方程中的常数项)看作正数的观念,常数项可正可负,不再拘泥于它的几何意义;同时根据题目需要,可以使用天元术列出高次方程,不再受到几何意义的影响;化简方程时能够使用方程两侧同乘一个式子的方法,把分式方程化为整式方程。
(2)从整体结构上来说,《测圆海镜》在卷一集中给出了各卷问题所需的定义、定理和公式,使该书基本上成为了一部演绎体系的著作,也是第一个构造体系的著作。
(3)先进的数学符号。数学的发展离不开数学符号,先进的数学符号可以有效地促进数学的进步。李冶在这一方面做出了重要贡献。在《测圆海镜》成书之前,我国的数码只有一到九,没有零,计算时遇到零,便空位,如果相邻有两个以上零的话,表述是不清楚的,这不利于我国古代数学的发展,在《测圆海镜》中,○的使用有两个作用,一是表示数中的空位;二是表示天元式或多项式中系数为零的项。使用“○”的记法使书中小数的记法在当时是比较先进的思想。在当时李冶的另一大成就就是负号的发明和使用。由于李冶掌握了一整套数字符号,使得他的方程可以用符号表示,改变了之前人们用文字描述方程的传统做法,使我国的数学进入了半符号化的时代,这对方程理论的发展具有重要的促进作用。[1-2]
《益古演段》与《测圆海镜》不同,它是李冶在封龙书院讲学过程中,发现《测圆海镜》中的内容不易被初学者掌握,为普及天元术而专门撰写的一部著作,是一部由浅入深、简明易懂、非常实用的数学教材。《益古演段》是在《益古集》的基础上,以天元术推演条段,利用新术和旧术对比的方法,加深人们对天元术的理解。《益古演段》共三卷64问,主要处理的是平面图形的面积、求所涉及图形的边长、圆径(直径)、周长等问题。内容编排先简后难,逐步加深。书中所涉及问题的解法均采用了新、旧术并列的方法分别进行求解。新术指的是天元术,旧术指的是条段法。书中各题包括“法”、“依条段求之”、“条段图”、“义”等四大部分,其中“法”是天元术;“依条段求之”是利用人们易懂的几何方法(条段法)对天元术进行解释,条段法是一种通过面积图形的分割、拼补寻找等量关系,以便求得方程各系数的图解法;在当时,条段法是大家比较常用的解题方法;“条段图”是根据条段法所画出的方程各项系数几何关系的图解;“义”是对图中已知量的文字说明。[1-2]《益古演段》无论是从内容安排上,还是在书中具体问题的解答过程中,都充分体现了李冶“晓然示人”先进的教育理念和优秀的教育方法,对我们当代无论是中小学教育还是大学教育都具有很好的启示作用。
数学并没有给李冶带来功名利禄,在现存的史料和记载中也未能发现他的学生有从事数学研究的,其两本算书都是在他去世后才出版的。祖颐为朱世杰《四元玉鉴》写的序中提到天元术发展的过程,但遗憾的是也未能提到李冶的名字。
二、李冶先进的数学思想
与之同时代的秦九韶不同,李冶从未有对数学的历史、起源、奇闻逸事等进行过评论,而是把重点放在驳斥世人对数学的错误认识以及他本人写算书的心态与研究数学的方式与方法上。
(一)施之人事,最为切务
李冶对数学的应用有切身的体会。他在任钧州知事期间,战事比较紧张,物资调度十分频繁。他掌管出纳,“无规撮之误”。这说明他有很好的数学和计算功底。《益古演段·自序》:“术数虽居六艺之末,而施之人事,则最为切务,故古之博雅君子马、郑之流未有不精研于此者也。”而在《测圆海镜·序》:李冶写到“由技兼于事言之,夷之礼,夔之乐,亦不免为一技;由技进乎道者言之。石之斤,扁之轮,非圣人之所与乎?”充分地表达了他研究数学的决心和毅力。此外,李冶能够充分认识到其算书对后人的作用,临终前他衷心地嘱咐儿子:“吾平生著述,死后尽可燔去,独《测圆海镜》一书,虽九九小数,吾尝精思致力焉,后世必有知者,庶可布广垂永乎?”(《测圆海镜·王德源后序》)[1-2]
(二)晓然示人,尽轩隶之秘
李冶认识到数学的重要性,并且想让自己的算书布广垂永,推广天元术,撰写了《益古演段》。李冶在研究当时算书的过程中,发现它们普遍存在两大缺陷:
(1)“今之为算者,未必有刘(徽)、李(淳风)之工,而褊心踞见,不肯晓然示人,惟务隐互错糅,故为溟滓黯,惟恐学者得窥其仿佛也。”李冶《益古演段》之前的数学著作《益古集》就属于这种情况,李冶在此基础上,撰写了《益古演段》,对天元术的推广做出了重要贡献。
(2)“不然则又以浅近粗俗无足观者,致使轩辕隶首之术,三五错综之妙,尽堕于世井沾沾之儿,及夫荒村下里蚩蚩之民,殊可悯悼。”(《益古演段·自序>),对于这种情况,李冶是针对当时的民用数学、商用数学而言的。为了满足社会的商业经济发展及日常生活需要,数学的实用性增强,越来越贴近平民百姓。[1-2]
(三)数学是能够认识的
李冶的数学思想受到了道家哲学的影响,认为数学是能够认识的。在《测圆海镜·序》中李冶对数学在哲学上的意义,论述得尤为深刻。书中写到“数本难穷,吾欲以力强穷之,彼其数不惟不能得其凡,而吾之力且惫矣。然则数果不可以穷耶?既已名之数矣,则又何为不可穷也。故谓数为难穷,斯可;谓数为不可穷,斯不可。何则?彼其冥冥之中,固有昭昭者存。夫昭昭者,其自然之数也;非自然之数,其自然之理也。数一出于自然,吾欲以力强穷之,使隶首复生,亦末如之何也已。苟能推自然之理,以明自然之数,则虽远而乾端坤倪,幽而神情鬼状,未有不合者矣。”李冶清醒地认识到数学来于自然,自然是有规律可循的,也是可认识的;他认为研究数学要得法,必须遵循自然规律,不可以力强穷之。[1-2]
(四)“因材劝学”的教育理念
李冶的思想是融合了儒、道以及其他体系的思想,由于受到儒家思想的影响,他对人性论,特别是对孟子的善恶论做了深入思考。李冶认为,真正的善恶贤愚,在人之初都是不存在的,可以通过后天的培养和学习形成。因此,可以根据人的不同情况进行有效的诱导,达到劝人为善的目的。[1]李冶将此观点应用到了教学当中,他说:“大抵今之学非古之学也,今之学不过为利而勤,为名而修尔。因其所为而引之,则吾之劝之者易以入,而听之者易以进也。”李冶以“为利”、“为名”来鼓励中下者学习充分反映了顺应人的本性,因材劝学的思想,这一思想虽有功利之嫌,但也有我们所值得借鉴的地方,因为这一思想与当代高校所提倡的因人施教、因材施教思想极为接近,其目的都是为了提高教学效果。
三、李冶先进的数学教育思想对当代大学数学教育改革的启示
(一)对“晓然示人”理念的新理解
在《益古演段》序言中,李冶写道“今之为算者未必有刘、李(指刘徽,李淳风)之功,而褊心局见。不肯晓然示人,惟务隐互错糅,故为溟涬黯黮,惟恐学者得窥其彷佛也 ”。李冶却认为“使粗知十百者,便得入室啖其文,顾不快哉。”充分体现了李冶“晓然示人”的先进教育理念。在当代教育中,我们所需要考虑的是如何更好地“晓然示人”。就大学数学教育而言,由于该课程自身具有较强的抽象性、逻辑性等特点,使大学生学习数学不得其法。这值得大学数学教师深入研究讲授大学数学的教学思想和教学方法。作为一名高校教师,应在深度和广度上加深对课程的理解和把握。
本文先对我国目前地理信息资源成果管理的现状进行了分析,在对地理信息成果进行管理时,以数据库与基础测绘数据库等设置为数据来源,并以数据中心为基础利用数据仓库的方法对地理信息数据进行统一的管理,在大数据时代对多样化数据、海量数据的管理提供了科学合理的方式,提升我国地理信息管理效率。
(1)在深度上,首先教师应充分理解掌握所讲授的内容,能够用学生容易接受的语言对讲授的内容进行讲解,也就是将数学语言形象化;其次,了解相关知识的产生背景,以便在讲授过程中,灵活引入历史元素,加深学生对知识的理解。
(2)在广度上,教师应了解数学在相关学科中的应用实例,以便对所教专业的学生开展有针对性的数学课程教育,因材施教。例如在讲授导数时,对于理工科的学生,可以引入变速运动中速度与路程的关系问题;对于经济类专业的学生,则应联系边际成本和边际效益讲授导数的思想。此外,在教学过程中有机地引入数学建模思想,使学生深刻理解数学在培养其良好的思维方法和后续课程学习与应用中的重要性。这样组织数学教学,有利于学生将先进的数学思想和方法应用于后续专业课程的学习与研究之中。
(二)形象化地讲授数学思想
在《益古演段》中李冶使用形象的几何法来解释天元术,以此普及天元术,正如书中提要所说:“此法虽为诸法之根,然神明变化,不可端倪,学者骤欲通之,茫无门径之可入。惟因方圆幂积以明之,其理尤属易见。”李冶的《益古演段》旨在借助“方圆幂积”,建立通向天元术这一数学思想的桥梁,而不在其变化的解题方法上。在当代大学数学教学中,数学思想是学好数学,用好数学的关键。因此,如何让学生更好地理解数学思想,成为高校数学教师应认真研究的重要课题之一。《益古演段》给我们留下了很好的范例。大学数学具有很强的抽象性,在讲授过程中可以把抽象的概念和思想形象化。例如在极限的思想中,可以引用李白的《黄鹤楼送孟浩然之广陵 》中“孤帆远影碧空尽”,在唯美地画卷中体会极限思想。矩阵的概念和运算是线性代数中的一个重要概念,而且与行列式的概念容易混淆,在教学的过程中可以借助生活中的实例进行讲解,例如某家电公司向三个商场发送四种产品的数量如表1。
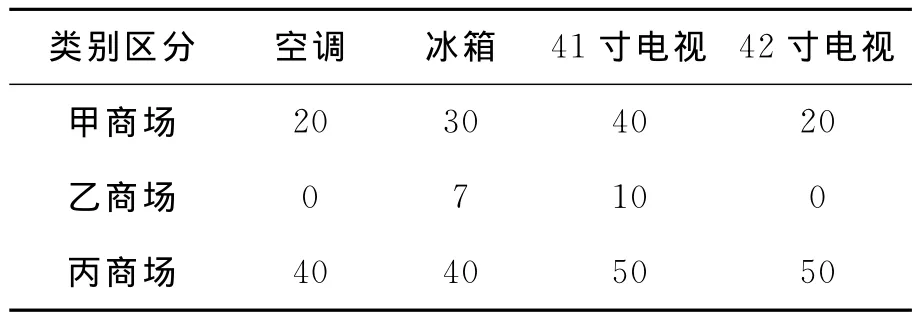
表1 三个商场发送四种产品的数量
在教学手段和方法上,利用先进的教育技术辅助教学,特别是多媒体教学,可以将一些板书无法实现地连续变化过程清晰的呈现给学生,使其更好地理解和掌握教学思想。例如,讲授定积分的定义,用板书很难演示无限细分的过程中与面积真实值的近似程度,使用多媒体课件教学,就可以将此过程逼真地演示出来,学生可以更加直观形象地理解定积分中“微分法”的思想。
(三)对比法的新理解和应用
在《益古演段》中,李冶充分使用条段法和天元术相对比的方法,对天元术进行阐述,使人们更好地理解和应用天元术,同时也是使用条段法对天元术的论证。对比法对于当代大学数学教育仍然不落后,它不仅能够使用在解题运算过程中,在对新知识、新理论的讲授过程中同样也可以灵活运用,而且可以通过新旧知识的对比,加深学生对新知识的理解和掌握。
矩阵的初等变换是矩阵论的一个重要内容。笔者在教学过程中发现,对于学生来说如何利用矩阵的初等变换将矩阵化为行阶梯型或最简型是一个难点。利用高斯消元法解线性方程组,学生比较熟悉,可先将矩阵写成方程组的形式,利用解线性方程组与矩阵的初等变换相对比的方法,阐述将矩阵化为行阶梯型和行最简型,例如:

上述把矩阵A化为行阶梯型矩阵的过程可以看作对A对应的线性方程组

实施消元的过程。如下
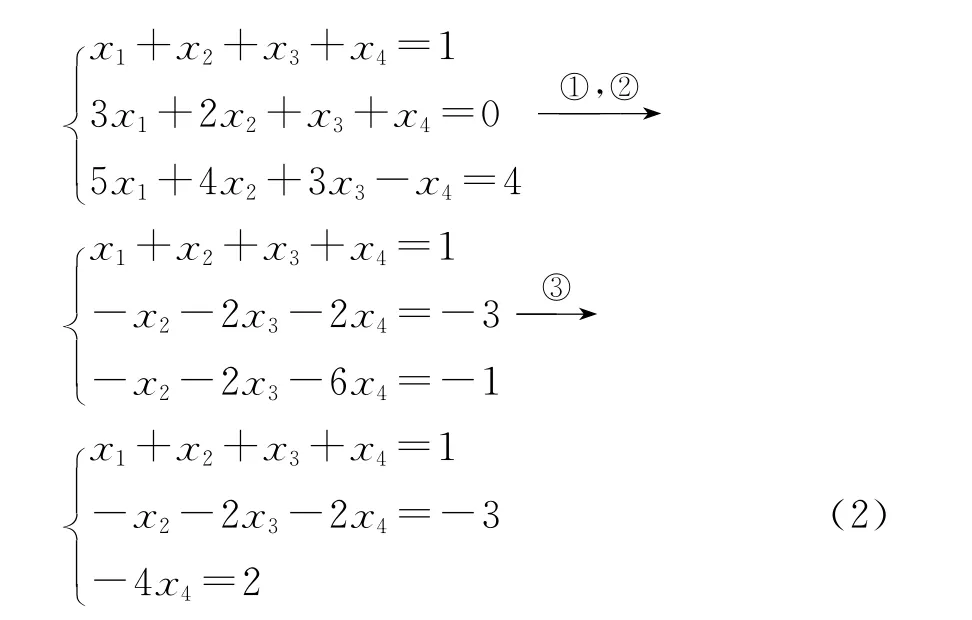
其中,①表示第二个方程减去第一个方程的3倍;②表示第三个方程减去第一个方程的5倍;③表示第三个方程减去第二个方程。
(2)式为方程组的行阶梯型方程组,矩阵(1)为行阶梯型矩阵。由上述对比过程可以看出利用初等变换化矩阵为行阶梯型的过程与解线性方程组的过程类似。利用这种对比方法,可以使学生清晰地掌握化矩阵为阶梯型的解题思路,使复杂的问题简单化。
李冶先进的教育思想不仅仅局限于以上几点,还有待当代大学数学教育工作者做进一步深入挖掘和研究,借此促进高校教师对当代大学数学教育改革做更加深入的思考和研究,切实加强数学教育教学方法改革,使大学数学学科真正成为广大学生所喜闻乐见的课程。
[1]孔国平.李冶朱世杰与金元数学[M].石家庄:河北科学技术出版社,2000:36-230.
[2]孔国平.李冶传[M].石家庄:河北教育出版社,1988:8-35.
[3]孔国平.测圆海镜导读[M].武汉:湖北教育出版社,1996:51-53.
[4]李忠定.线性代数与几何[M].北京:中国铁道出版社,2011:37-40.
