采用人工神经网络方法建立加氢裂化反应体系模型

王天宇，刘忠保，黄明富，李国庆

(1.中海石油炼化有限责任公司惠州炼化分公司，广东 惠州 516086；2.华南理工大学化学与化工学院；3.中国石油规划总院)

采用人工神经网络方法建立加氢裂化反应体系模型

王天宇1，刘忠保2，黄明富3，李国庆2

(1.中海石油炼化有限责任公司惠州炼化分公司，广东 惠州 516086；2.华南理工大学化学与化工学院；3.中国石油规划总院)

用BP神经网络技术建立了某2.80 Mt/a蜡油高压加氢裂化装置反应系统模型，该模型可较好地预测原料量、各段反应器进口温度和冷氢导入量对系统产品分布和各段反应器出口温度的影响，模型精度较高，温度预测误差小于0.1 ℃，并具有较好的再现性及泛化能力，可以用于指导生产操作。

石油馏分 加氢裂化 神经网络 数据挖掘 预测 建模

加氢裂化是在较高温度、压力下，烃分子与氢气在催化剂表面进行裂解和加氢反应生成较小分子的转化过程[1]。由于其原料适应性强、轻油收率高、产品质量好，越来越受到重视。截至2012年6月，我国三大石油公司就已投产36套高、中压加氢裂化(改质)装置，总加工能力超过50 Mt/a，并还有20余套正在设计和建设中，总加工能力接近40 Mt/a。

生产和技术发展极大地促进了加氢裂化机理研究。其中，基于集总理论(Lumping)的建模研究最引人注目[2-6]，它根据反应体系中各类分子的动力学特性不同，将其划分成若干个虚拟组分即集总，再视每个集总为单一组分，从而建立起反应体系动力学模型。由于将复杂反应体系抽象为可数的单一集总组分间的反应，故定量研究成为可能。但受制于石油馏分高度复杂，反应机理尚不明了，以及模型参数难于确定等原因，集总理论加氢裂化机理研究尽管取得了很大成就，但仍面临许多困难，而因带动了黑箱模型(Black model)和混合模型(Mixed model)的发展。

黑箱模型是无视过程机理，单纯用统计学或人工智能的方法仿真其过程输入、输出关系的模型[7]。目前在加氢裂化领域应用最多的黑箱模型是BP人工神经网络(按误差逆传播算法训练的多层前馈型人工神经网络)[8-10]。由于它能借助样本数据实现Rn空间到Rm空间的高度非线性映射，且效果可以用足够的训练样本保证，故应用最广[11-13]。而混合模型则是机理模型和黑箱模型的折中，混合模型示意见图1[14-15]。

图1 混合模型示意

事实上，3种模型各有利弊。机理模型致力于过程本质描述，但又不得不借助假设(如集总)，因而误差大，且有自身尚不能克服的困难(如设备边界条件的数学描述等)；黑箱模型无视过程机理，相对简单，但只能针对特定的I/O数据进行分析，因而结论不具外延性；黑箱模型企图集大成，但结构复杂、收敛困难。

本课题采用BP神经网络技术建立某蜡油高压加氢裂化装置反应体系模型，并探讨其预测结果的再现性和泛化能力，以指导生产操作。

1 人工神经网络模型的建立

图2是某2.80 Mt/a高压蜡油加氢裂化装置反应系统的原则流程示意。由图2可见，原料经6个串级反应器床层，在催化剂的作用下发生精制和裂化反应，最终得到气体、LPG(液化气)、轻石脑油、重石脑油、喷气燃料、柴油和尾油等产品。

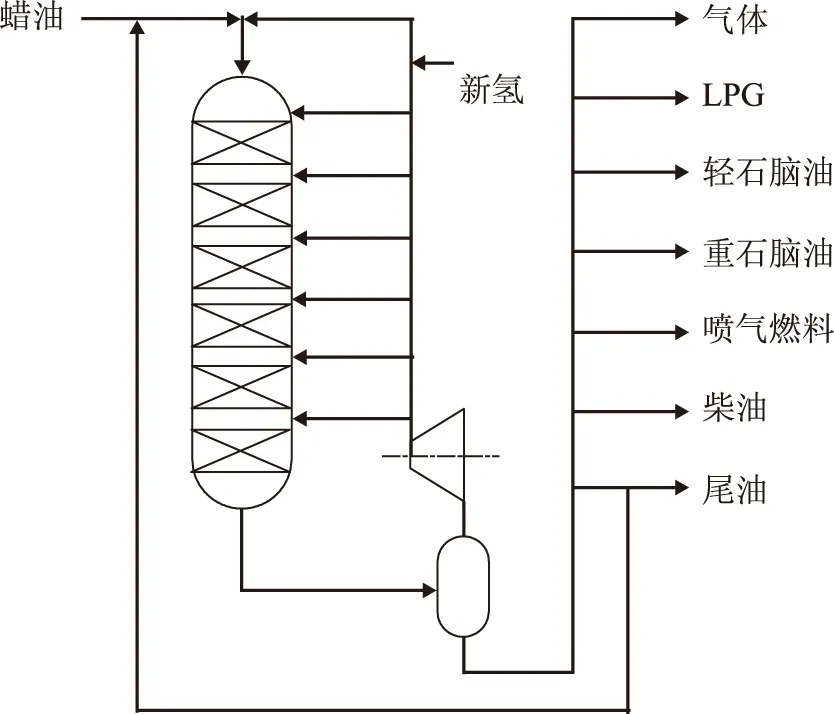
图2 某加氢裂化反应系统原则流程示意

1.1 人工神经网络

人工神经网络是模拟生物大脑神经网络结构和功能而建立的一种智能运算理论，它包含输入层、隐藏层(一个或多个)和输出层(见图3)，其目的是通过神经元运算，学习输入输出数据，使预测值最大限度地与实际值一致(见式1)。人工神经网络学习的目的是找出隐含在数据背后的规律，对具有同一规律的学习集以外的数据，神经网络仍具有正确的响应能力，称为泛化能力[16-17]。

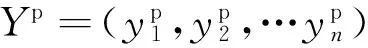
(1)

式中：W是权重矩阵；X是实际输入值矩阵；Yp是实际值矩阵；Y是预测值矩阵；F是激活函数。

图3 人工神经网络结构示意

上层神经元的输出通过激活函数激活后成为下层神经元的输入(同层间神经元之间没有输入输出关系)，所以人工神经网络的学习规则就是：确定合适的W以使输出误差最小。

建立工业过程人工神经网络模型的步骤是：①现场采集研究对象的I/O数据即X和Yp。尽量采集较大操作范围和较长时间区段内的数据；②数据预处理：原始数据不能直接用于识别，需过滤、筛选，以消除噪声数据；③确定人工神经网络结构：由于输入层节点数和输出层节点数分别是输入变量和输出变量数，因此人工神经网络的结构实际由隐藏层数和每个隐藏层所包含的节点数所决定；④训练模型：该过程是人工神经网络的学习过程，选若干组预处理过的数据，将输入变量导入输入层，人工神经网络会根据输出值与实际值误差自动调节权重，从而使误差最小。本课题使用BP算法进行训练，并在MATLAB平台上实现；⑤验证模型：将剩余数据导入模型输入层，对比输出值与实际值误差，检测模型精度。

用BP人工神经网络训练样本，隐藏层和输出层激活函数分别采用S型和简单线性函数[式(2)]。

f(x)=1/(1+e-x)
f(x)=x

(2)

S型函数连续可微，且f′(x)=f(x)[1-f(x)]。

1.2 模型建立

1.2.1 采集数据 通过对现场数据进行灵敏度分析，决定选取原料流量、第一至第六段反应器进口温度、第一至第六段急冷氢流量共13个参数作为自变量，研究它们对第一至第六段反应器出口温度和尾油、柴油、喷气燃料、重石脑油、轻石脑油、LPG、干气、低压分离气(低分气)以及总气体流量共15因变量的影响。对图2所示系统进行现场数据采集，每天从DCS(分散控制系统)采集一次，连续105天，共计采集正常运行数据105组。数据统计情况如表1所示。

影响装置反应器出口温度及产品分布的因素还包括原料的馏程、氢气纯度、催化剂活性。但数据采集期间，装置运行稳定，原料的馏程基本保持不变，因此不作为研究对象。循环氢纯度维持在89.91%～90.15%，新氢纯度维持在99.94%～99.96%，循环氢、新氢纯度变化很小，为简化模型，不选用氢气纯度作为研究对象。该套装置使用的催化剂更换周期是两年，数据采集期间催化剂均处于装置运行初期，催化剂性能差异较小，因此不考虑催化剂活性对研究对象的影响。

1.2.2 确定隐藏层节点数 为了简化，人工神经网络一般采用单隐藏层结构，故13个输入变量和15个输出变量条件下，网络的结构由隐藏层节点数确定。本课题用试验法寻找最佳隐藏层节点数。为此将表1数据随机分成两组，一组含70组数据用于训练，一组含35组数据用于检验。分别取隐藏层节点数从8到12，隐藏层节点数对模型误差的影响结果见表2。由表2可见，隐藏层节点数等于10时，输出变量预测值与测量值的误差最小，且左右偏离越大，误差越大。所以本模型选定隐藏层节点数为10。

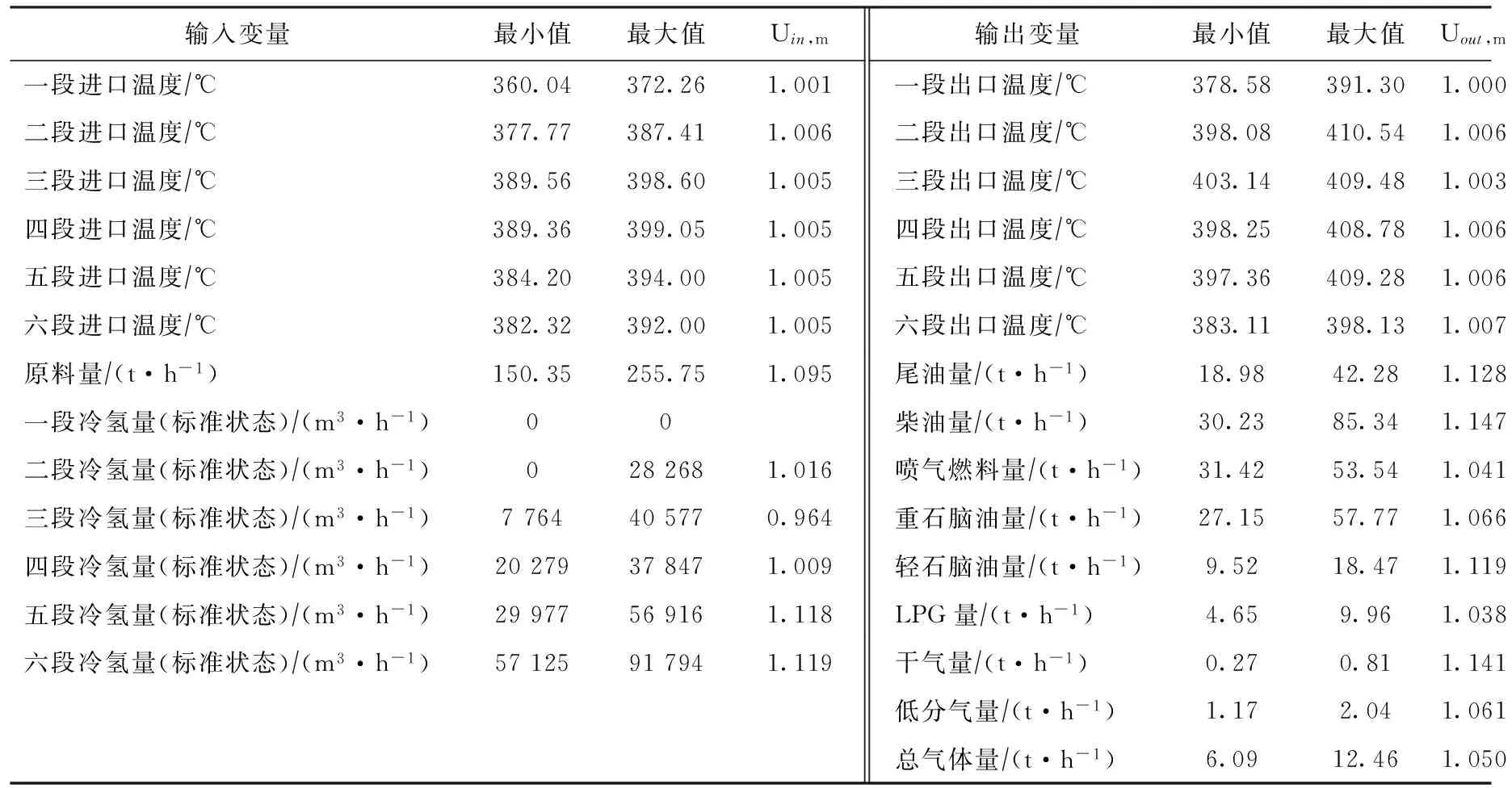
表1 现场采集的反应系统输入输出数据的统计情况

注： uin，m和uout，m分别是输入、输出变量之中位数与平均数的比值，看得出来它们均接近1，说明各变量在取值范围内分布较均匀，利于模型分析。

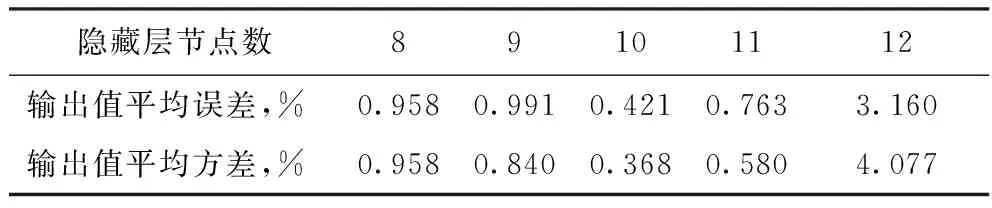
表2 隐藏层节点数对模型误差的影响

表2中，输出值平均误差和平均方差分别用式(3)和式(4)计算。

(3)

(4)

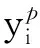
图4是拟将采用的人工神经网络结构示意。

1.3 模型运算

将表1中任意70组数据导入图4模型，经训练得到权重W，然后将剩余的35组数据的输入变量导入，计算其输出。表3给出了相应的误差统计。

表3 ANN计算输出与实际测量的误差统计

表3中，相对误差(μ)和标准差(ϖ)分别采用式(5)～(7)计算。

(5)

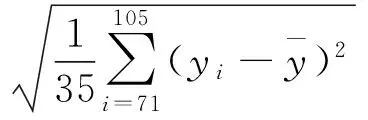
(6)

(7)

从表3可以看出，该模型对反应器出口温度和重质产品如尾油、柴油、喷气燃料、重石脑油的产量预测十分精确，最大相对误差只有0.087%(喷气燃料量)。尤其是温度，平均相对误差只有0.02%，折成绝对误差不到0.1 ℃。但对轻质产品如轻石脑油、LPG、干气、低分气产量预测要差一些，其中干气的相对误差最大，为3.316%。

图5～图7给出了几个输出变量及误差的分布(图中，横坐标71到105表示用于验证模型的35组数据的编号)。

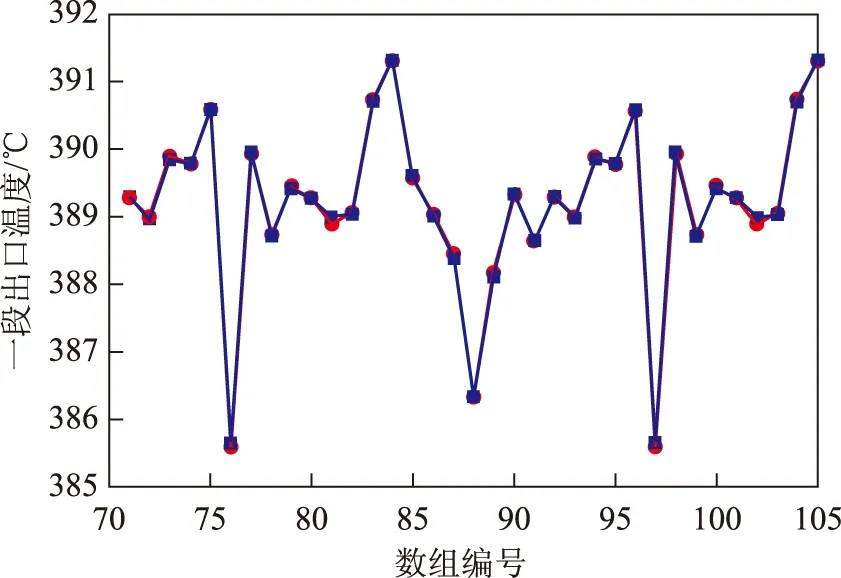
图5 一段反应器出口温度及误差分布■—测量值； ●—预测值。 图6、图7同

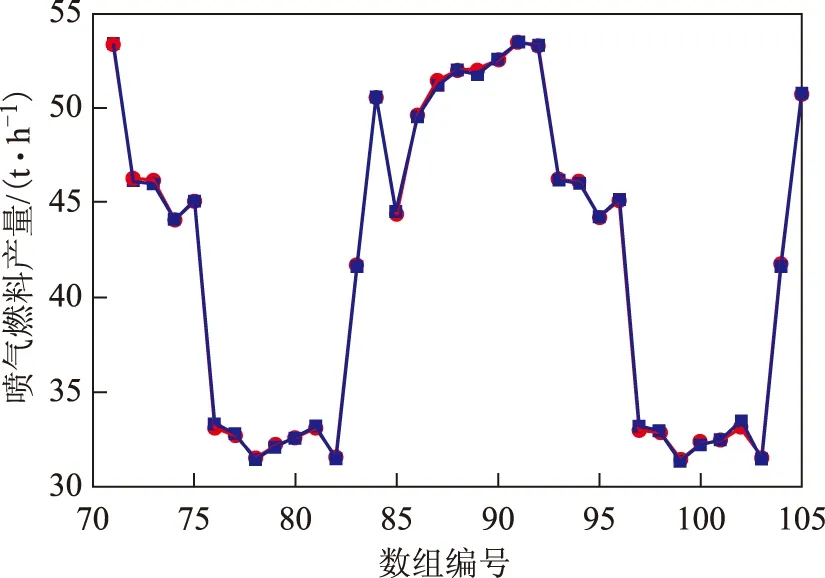
图6 喷气燃料产量及误差分布

图7 总气体产量及误差分布

1.4 模型的重复性

ANN计算受制于训练样本的选择、隐藏层节点数的多少和迭代次数等，因此模型的稳定性判断十分必要，其重复性是重要的参考之一。重复性是指同一操作者在相同实验条件下多次测定结果之间的分散程度，相对标准偏差越小则分散程度越低，表明重复性好[18-19]。表4给出了迭代次数同为240次时的3次计算结果(如果在240次前收敛，则将该组数据剔除)，从表4可以看出，3次测试之间的误差很小，标准偏差最大为2.912%，表明模型的重复性好。

表4 本ANN模型3次计算结果的相对标准偏差统计

1.5 模型的泛化能力

本质上讲ANN是数据依赖的，即所采集的研究对象的I/O数据不同，描述该对象的模型将不同。但实际生产过程又是无法复制的，因此从指导和优化操作的角度讲，无不希望ANN模型具有一定的泛化能力，能用于预测和指导数据采集期后的操作(当然生产方案无变化，且操作稳定)。

下面以一段进口温度改变为例进行考察。一段进口温度间接反映了反应进料加热炉的出口温度，是实际生产过程的关键调节手段之一，其温度高低直接影响反应系统的温度分布和产品分布。为此，重新采集100组数据(见表5)，并从中选取两组一段进口温度偏差较大，但其余输入偏差较小的数据，即表5中的第一行数据，一段进口温度由360.35 ℃提高到369.65 ℃，对应尾油量由36.07 t/h降到33.56 t/h，喷气燃料量由48.12 t/h增加到55.59 t/h，与用原模型计算得到的预测值基本符合。说明该模型对一段进口温度变化具有较强的泛化能力。

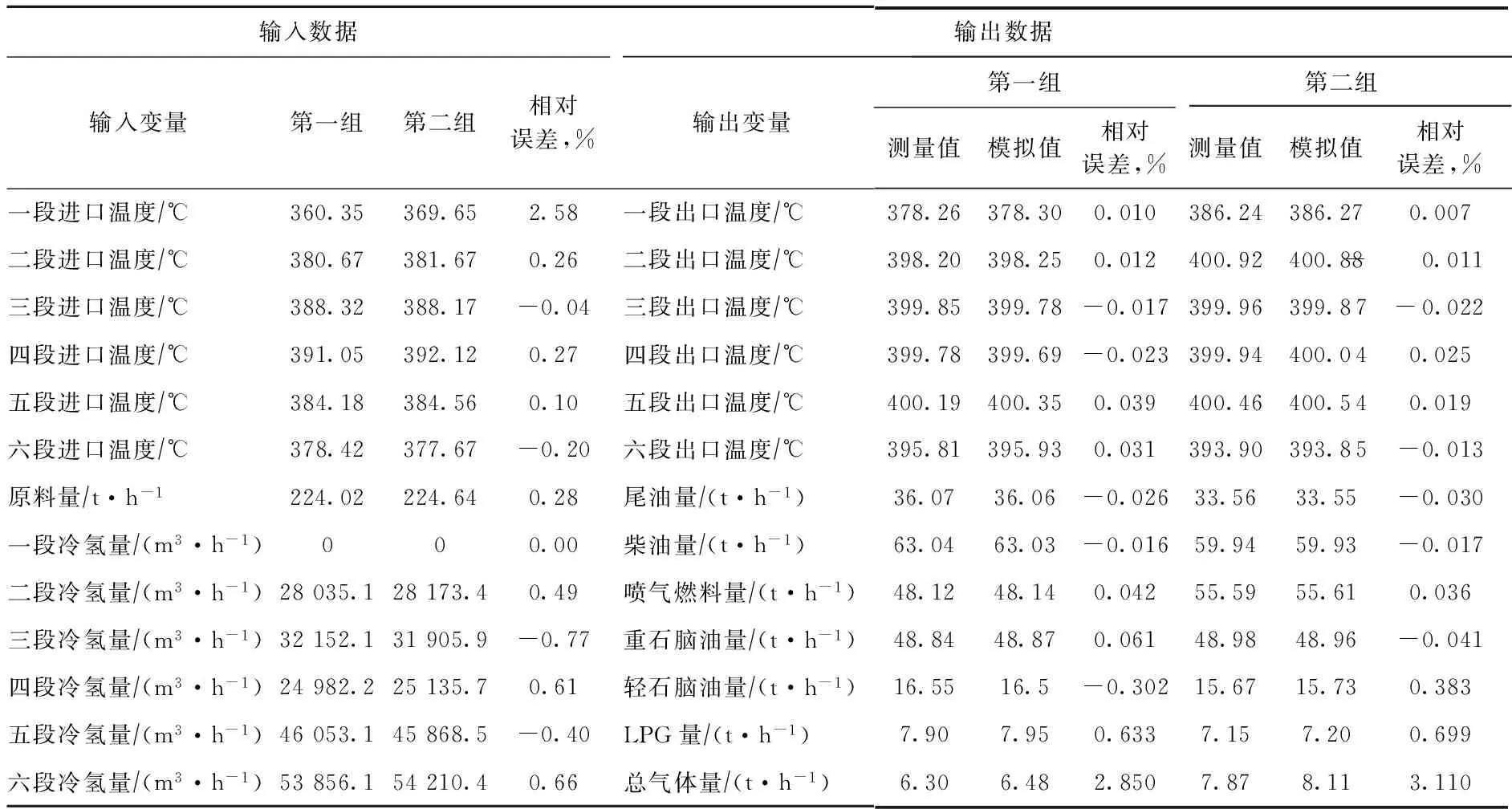
表5 现场采集的另外100组反应系统输入、输出数据的模拟情况

2 结 论

(1) 使用BP-ANN技术对某2.80 Mt/a六段蜡油高压加氢裂化装置反应系统进行了建模。模型以原料量、各段反应器进口温度和冷氢流量共计13个变量为输入变量，以系统产品分布和各段反应出口温度共计15个变量为输出变量。并采用单隐藏层结构，使用连续可微的S型函数作为隐藏层激活函数，简单线性函数作为输出层激活函数。

(2) 从现场采集了105组I/O数据，并将其随机分成两组，一组含70组数据用于训练，一组含35组数据用于检验。计算发现隐藏层节点数为10时，输出变量预测值与测量值的误差最小，故确定本模型的隐藏层节点数为10。

(3) 计算结果表明本ANN模型的精度较高，对反应器出口温度和重质产品如尾油、柴油、喷气燃料、重石脑油的产量预测十分精确，最大相对偏差只有0.087%(喷气燃料量)。尤其是温度，绝对误差不到0.1 ℃(机理模型偏差一般在5 ℃左右)。但对轻质产品如轻石脑油、LPG、干气、低分气的产量预测较差，干气产量预测误差最大，相对误差为3.316%(但机理模型的误差通常在10%～20%)。

(4) 检验结果表明本模型具有较好的再现性，迭代次数同为240次时的三次计算结果的平均相对误差最大只有0.483%，表明模型在训练完成后导入输入变量，能够对输出变量做出较稳定的预测。

(5) 不同一段进口温度的计算结果表明本模型具有较好的泛化能力，能够用于预测和指导数据采集期后的操作。

[1] 林世雄.石油炼制工程[M].北京：石油工业出版社，2000：389-391

[2] Pacheco M A，Dassori C G.Hydrocracking：An improved kinetic model and reactor modeling[J].Chem Eng Commun，2002，189(12)：1684-1704

[3] Bhutani N，Ray A K，Rangaiah G P.Modeling，simulation，and multi-objective optimization of an industrial hydrocracking unit[J].Ind Eng Chem Res，2006，45(4)：1354-1372

[4] Martens，G G，Marin G B.Kinetics and hydrocracking based on structural classes：Model development and application[J].AIChE J，2001，47(7)：1607-1622

[5] 彭冲，方向晨，韩龙年，等.减压蜡油加氢裂化六集总动力学模型研究[J].石油炼制与化工，2014，45(1)：35-41

[6] Han Longnian，Fang Xiangchen，Peng Chong，et al.Application of discrete lumped kinetic modeling on vacuum gas oil hydrocracking[J].China Petroleum Processing and Petrochemical Technology，2013，15(2)：67-73

[7] 夏勇.加氢裂化反应器建模与优化研究[D].广州：华南理工大学，2012

[8] Liu Yibin，Tu Yongshan，Li Chunyi，et al.Catalytic cracking and PSO-RBF neural network model of FCC cycle oil[J].China Petroleum Processing and Petrochemical Technology，2013，15(4)：63-69

[9] 费卫峰，娄慧茹，陈青，等.人工神经网络用于化工中非线性模型建立的研究[J].石油规划设计，1997(1)：30-32

[10]张忠洋，李泽钦，李宇龙，等.GA辅助BP神经网络预测催化裂化装置汽油产率[J].石油炼制与化工，2014，45(7)：91-96

[11]杨建刚.人工神经网络实用教程[M].杭州：浙江大学出版社，2001：47-50

[12]Zhang Lei，Liu Zongkuan，Gu Zhaolin.Simulation of low-temperature coal tar hydrocracking in supercritical gasoline[J].China Petroleum Processing and Petrochemical Technology，2013，15(4)：70-76

[13]常凯.基于神经网络的数据挖掘分类算法比较和分析研究[D].合肥：安徽大学，2014

[14]李晓光.混合建模方法研究及其在化工过程中的应用[D].北京：北京化工大学，2008

[15]王寅.化工过程混合建模问题研究[D].杭州：浙江大学，2001

[16]Haykin S.Neural Networks：A Comprehensive Foundation[M].2nd edition.Prentice Hall，1999：23-29

[17]王迎春，耿长福.一种具有较强泛化能力的神经网络模型研究与应用[J].航天控制，2002(2)：6-11，17

[18]贾绍华，李静静.测量系统重复性与再现性在产品质量管理中的应用[J].大连交通大学学报，2010(5)：96-100

[19]曹生现.冷却水污垢对策评价与预测方法及装置研究[D].保定：华北电力大学(河北)，2009

MODELING VGO HYDROCRACKING PROCESS BY BP-ANN TECHNOLOGY

Wang Tianyu1， Liu Zhongbao2， Huang Mingfu3， Li Guoqing2

(1. Huizhou Petrochemical Company， CNOOC， Huizhou， Guangdong 516086；2. Chemistry and Chemical Engineering School， South China University of Technology；3. Planning and Engineering Institute of China National Petroleum Corporation)

The highly complexity of petroleum hydrocracking process results in the application of artificial neural network (ANN) in this field. In this paper a BP-ANN was used to model a VGO hydrocracking unit with a capacity of 2.8 Mt/a. The effect of feed rate， inlet temperatures of reactors， and amount of quench H2used on product distribution and outlet temperatures of reactors were well predicted by the model. The results show that the model has a higher accuracy， especially in the prediction of temperatures (less than 0.1 ℃) and a good ability of reproducibility and generalization ability and that the model is able to guide practical operation.

petroleum fraction； hydrocracking； neural network； data mining； prediction； modeling

2014-12-15； 修改稿收到日期： 2015-04-01。

王天宇，主要从事炼油技术和节能管理工作。

王天宇，E-mail：wangty2@cnooc.com.cn。