大型龙门机床的直线度误差建模及误差补偿
2015-09-03冯文龙沈牧文姚晓栋杨建国
冯文龙,沈牧文,姚晓栋,杨建国
(上海交通大学机械与动力工程学院,200240上海)
随着制造业对加工精度要求的日益提高[1-2],作为加工机床床身的大型龙门母机的精密程度直接决定着新生产机床的精度等级,关系到整个工业的生产水准.而对于加工速度相对较慢的龙门机床来说,直线度误差是决定机床加工精度的关键因素[3].直线度误差是指直线上各点跳动或偏离理想直线的程度[4-6].假定理想的移动路径为直线,在直线水平方向的偏移量称做水平直线度,垂直方向的偏移量称做垂直直线度.对于数控机床而言,导轨的凹凸不平导致轴在运动时会产生两个垂直于运动方向的偏移量,引起刀具和工件间距离在这两个方向上产生偏差,因此而产生的误差叫做机床直线度误差.传统的减小机床直线度误差的方法是通过对机床导轨垫垫铁的方式[7],然而该方法操作繁琐,解决问题能力有限,而且也只能解决上母线偏差,无法解决侧母线偏差.对于已加工好的导轨,一般通过刮研[8]方法提高导轨精度,这种方法不仅耗费人力,而且效率低,不适合用于大规模生产.相比之下,通过补偿方式来减小机床直线度误差更便捷有效[9-11].Cao[12]等提出了基于在线测量的直线度误差补偿方法,通过把在线测量出的直线度误差数据输入到Numerical Control(NC)程序中,进行补偿并且获得了68 nm/400 mm的良好补偿效果.但是,在线测量无法运用到实际大规模生产中,且通过更新NC程序的方式来补偿的方式实时性不强.由凤玲[13]等提出了一种新的测量直线度误差方法,该方法在公共路径上对激光束的偏移进行补偿,对光路上的空气扰动和温度变化具备很强的抗干扰能力,提高了直线度误差测量精度.Gao[14]等对基于空气导轨的工作台进行了俯仰、偏摆、滚转及两个方向直线度的测量,并分别使用两种不同的测试方法来保证测试结果的可靠性;还分析了转动误差对直线度误差测量的影响,并提出了通过把渥拉斯顿棱镜摆放在运动部件上来避免转动误差在测量直线度误差过程中的影响.但均未对产生的直线度误差进行补偿.
本文使用激光干涉仪分别检测大型龙门数控机床3个坐标轴沿6个方向的直线度误差,应用B样条曲线建立直线度误差模型,通过在空间上矢量叠加得到该机床直线度误差空间模型.利用数控系统外部机械原点偏移功能[15],通过自主研发的误差实时补偿系统并依据提出的基于B样条曲线的空间直线度误差模型,实现了对大型龙门数控机床空间直线度误差补偿.经补偿加工,机床加工精度有大幅提高.
1 基于B样条曲线的空间直线度误差模型理论及分析
1.1 平面直线度误差建模
B样条是样条曲线一种特殊的表示形式,它是B样条基曲线的线性组合,B样条是贝兹曲线的一种一般化[16-18].B样条曲线有着良好的数据拟合能力和局部可调整性,是理想的建模工具.非均匀B样条的数学表达式为

式中:C(t)/μm是机床直线度误差预测值,bj(j=0,…,n)/μm是B样条模型的控制节点,p是B样条模型的阶数,Nj,p(t)是定义在节点向量T={t0,t1,…,tn+p-1,tn+p}上的p阶 B 样条基,其表达式为
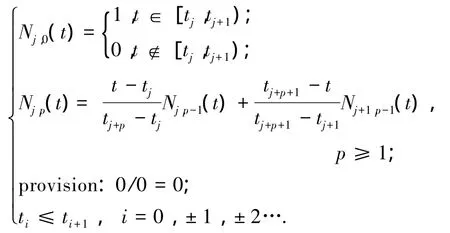
控制节点bj的选取过程如下:在给定的误差数据点Pi(i=0,…,m)中,选取一些能够表达数据几何信息的关键点作为B样条模型的控制节点,这些点往往包括局部曲率最大点(LMC)、拐点、端点等.在本模型中,2个端点和LMC点作为控制节点,初始控制节点数目设置为10个.对所有的误差数据点进行曲率ki的计算,如果ki>ki-1并且ki>ki+1,则判定该点为LMC点,把找到的所有LMC点根据曲率数值大小进行排序,提取前8个LMC点作为控制节点.把以上10个控制节点bj和计算所得的 B样条基Nj,p(t)代入式(1),即可得到B样条平面直线度误差初始模型.
为了检验模型的拟合精度,对模型残差进行量化分析,残差计算方法为
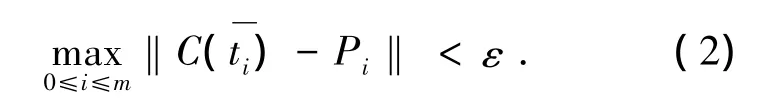
应用式(2)对每个测量点进行残差检验,如果所有的残差均在容许残差ε以内,则模型建立完成.如果有测量点的残差在容许误差以外,则把该测量点Pi加入到控制节点中,此时控制节点变成11个,模型按照以上过程重新建立,再次对残差进行检验,如果再有测量点残差在容许误差之外,再把该点加入控制节点,如此往复,直到所有的测量点残差均在容许误差以内.建模流程图如图1所示.
1.2 空间直线度误差建模
以三轴数控机床为例,机床任意一个运动轴运动都会产生两个方向的直线度误差,3个轴就有6个方向的直线度误差,分别是:X轴运动,沿Y、Z方向产生的直线度误差δy(x)和δz(x);Y轴运动,沿Z、X方向产生的直线度误差 δz(y)和δx(y);Z轴运动,沿X、Y方向产生的直线度误差δx(z)和δy(z).则空间直线度误差即可表示为以上6个直线度误差同方向的叠加,表达式为
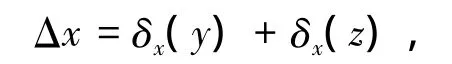



图1 B样条建模计算流程图
因此,不论X、Y、Z联动还是单独运动,工件和刀具在X、Y、Z方向上的直线度偏差分别是式中的Δx、Δy、Δz.对 δx(y)、δx(z)、δy(x)、δy(z)、δz(x)及δz(y)分别进行上述平面直线度误差建模,得到预测值δ'x(y)、δ'x(z)、δ'y(x)、δ'y(z)、δ'z(x)及δ'z(y),则空间直线度误差模型可表示为

2 机床直线度误差数据测量及数学模型建立
在一台大型龙门铣床上进行测试实验,该龙门铣床是工作台固定在地面,刀具固定在Z轴,Y轴在X轴上运动的TXYZ结构.该龙门铣床拥有双X轴、Y轴和Z轴.X轴的行程14 300 mm,Y轴和Z轴的行程分别为3 000 mm和2 500 mm.4个轴都带有光栅尺,困扰该龙门铣床的首要问题就是直线度误差.
考虑到实际加工状态和理想测试状态的区别,对X轴运动产生的直线度误差进行了两次测试.第一次测量,反射镜安装在主轴头上,机床零负载运行,测得一组误差数据.第二次测量,机床X轴运动,加工13 000 mm长的导轨平面,对该平面进行直线度误差测量,测得第二组误差数据.由图2可知,实际切削加工和机床空载条件下测出的直线度误差数据存在差异,考虑到加工环境的复杂性,而且最终目的是要生产出直线度较好的工件,故采用加工导轨后测得的直线度误差数据建模.
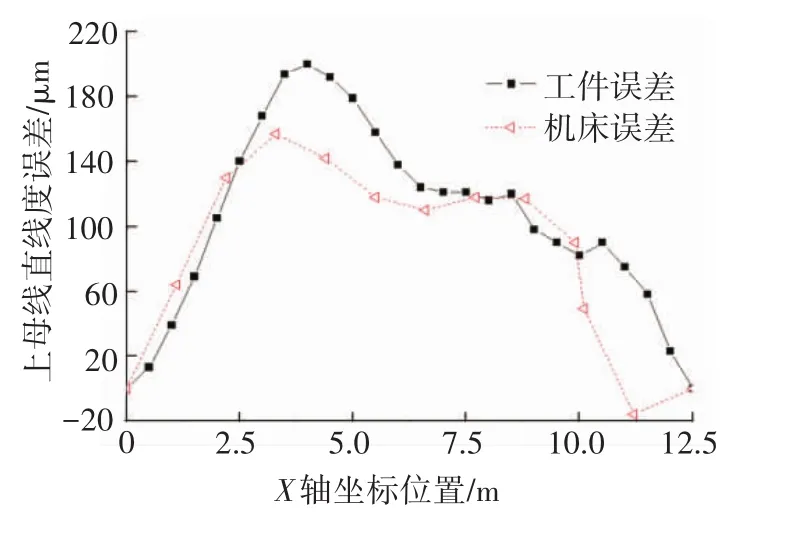
图2 工件直线度和机床直线度对比
对导轨表面进行切削加工,加工出一个新的平面,考虑到各方向直线度误差量级未知,水平面切削统一采用直径200 mm的铣刀,主轴转速1 000 r/min,进给速度 1 000 mm/min,切削量0.4 mm;垂直面切削统一采用直径50 mm的铣刀,主轴转速800 r/min,进给速度200 mm/min,切削量0.4 mm.X轴运动切削,Z方向的直线度误差就完全反映在新加工的水平面上.对新加工的水平面进行直线度误差测量,测得工件在Z方向的直线度误差 δz工(x).同理,切削一个新的垂直面,测得工件在Y方向的直线度误差δy工(x).换成Y、Z轴运动,同理可得到,Y轴运动Z方向直线度误差δz工(y)和X方向直线度误差δx工(y);Z轴运动X方向直线度误差δx工(z)和Y方向直线度误差δy工(z).对得到的6条直线度误差数据进行平面直线度误差建模.以X轴运动Z方向直线度误差δz工(x)建模为例,初始控制节点数目设定为10个,B样条模型为4阶,容许误差为9μm,则B样条模型由式(1)可得

建模结果如图3所示.

图3 不同控制节点的B样条模型残差对比
10个控制节点的B样条模型拟合精度不高,选取残差最大点作为第11个控制节点,重新建模后,拟合精度大幅提高,如此往复,直到达到残差容许值,此时的B样条模型表示为δ'z工(x).
同理可得其他各方向的B样条模型:δ'y工(x)、δ'z工(y)、δ'x工(y)、δ'x工(z)、δ'y工(z).图 4~9 为各直线度误差模型预测值和测量值之间的对比图
由图4~9可知,B样条模型有准确的预测直线度误差的能力,X轴Z方向直线度误差未补偿达到200μm,建模后残差减小到8.3μm;其他各方向直线度补偿后均有明显改善,X轴Y方向直线度误差从未补偿79μm减小到4.8μm;Y轴Z方向直线度误差从未补偿52μm减小到2.8μm;Y轴X方向直线度误差从未补偿25μm减小到2.4μm;Z轴X方向直线度误差从未补偿20μm减小到1.6μm;Z轴Y方向直线度误差从未补偿35μm减小到2.2μm.模型预测准确度在90%以上.
由式(3)可得该龙门铣床的空间直线度模型:
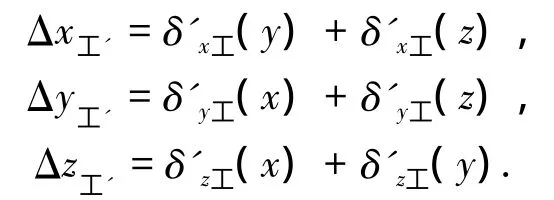
式中:Δx工'、Δy工'、Δz工'分别为空间任一点在X、Y和Z方向上直线度误差的预测值,模型覆盖整个空间场.
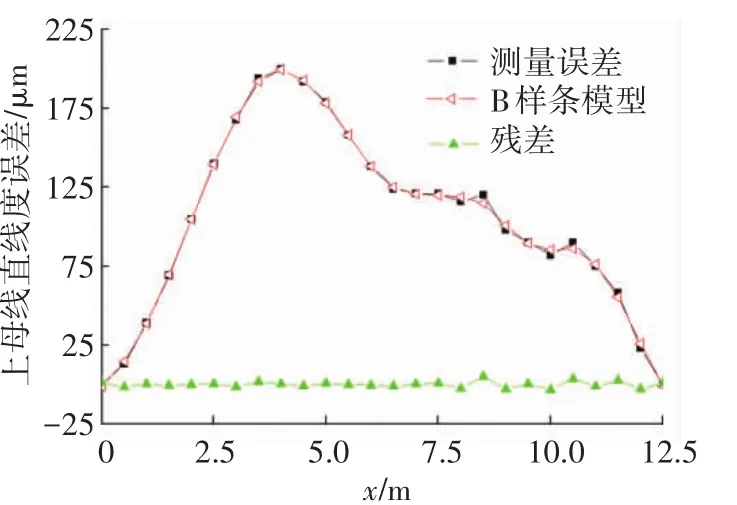
图4 X轴Z方向预测、实测直线度误差对比
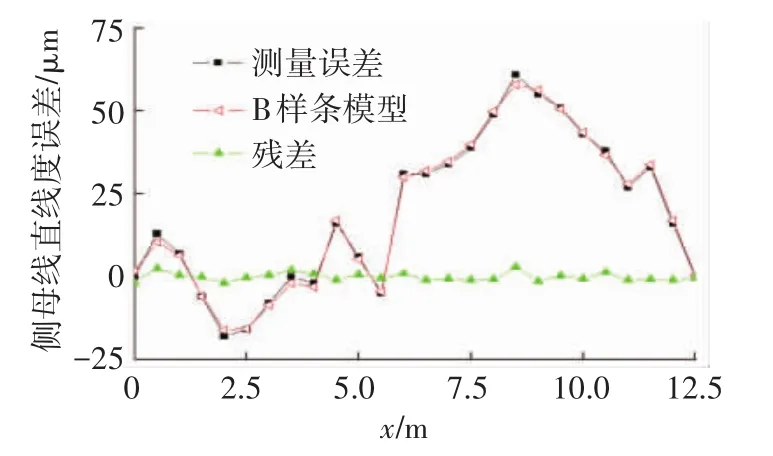
图5 X轴Y方向预测、实测直线度误差对比

图6 Y轴Z方向预测、实测直线度误差对比

图7 Y轴X方向预测、实测直线度误差对比

图8 Z轴X方向预测、实测直线度误差对比

图9 Z轴Y方向预测、实测直线度误差对比
3 补偿实验验证及模型对比分析
为了验证B样条模型的有效性和鲁棒性,本实验不再采用误差采集实验中的单轴运动模式,而采用两轴联动切削平面的方式,工艺切削参数较之前不变.以Z向直线度误差为例,误差采集实验是先采集X轴单独运动产生的Z方向直线度误差,再采集Y轴单独运动产生的Z方向直线度误差,在空间做矢量叠加,则空间模型中就得到了空间任一点的Z向直线度误差.而两轴联动切削实验是指X、Y轴联动,运动路径为XY形成的四边形对角线,切削一个垂直于Z向的平面,然后测量这个平面的Z向直线度误差.验证实验采用两轴联动切削平面方式的主要目的有两个:一是两轴联动切削是一种更复杂的工况,Z向的直线度误差同时受到X运动和Y运动的联合影响,而不是像误差采集实验中的单轴运动,受到单一因素影响,更有助于验证模型的鲁棒性;另一方面,如果验证方式采用单轴运动切削工件,补偿输出值是单方向直线度误差模型预测值,不涉及空间模型计算,验证不了空间模型的准确性.而如果采用两轴联动切削工件的方法,补偿值完全由空间模型自主运算得到,补偿的准确性完全依赖于模型的鲁棒性和准确性.
对切削完成的平面进行直线度误差测试,测试间隔距离选用240 mm,在直线度测试过程中,测试间隔距离以测试滑块两个接触点的距离为最佳,测试精度也最高,因此选用滑块长度240 mm为测试间隔距离.测试结果如图10所示.
图10中的3条曲线分别是使用B样条模型、7次多项式模型、斜线插补模型补偿后的残差曲线.B样条模型的补偿效果明显优于其他两种.
多项式模型具有较好的平滑处理能力,对补偿值的输出做了良好的规划,避免发生速度和加速度的突变,故相邻位置的残差变化较小,残差曲线较平稳,但是由于直线度误差数据往往都是无规则变化,多项式拟合的模型精度不高,残差较大.
斜线插补模型具有较高的建模精度,在每个测试点,直接补偿测量的误差值,各点之间用斜线插补.但是由于该模型是由多条折线组成,在过渡点存在明显的速度和加速度突变,在补偿输出时,容易对机械造成冲击,补偿值和真实运动值之间存在不匹配和延时效应,故各点残差存在剧烈跳动、阶跃.斜线插补模型补偿后,短距离直线度偏差过大,严重偏离5μm/m的国家标准,残差较大.
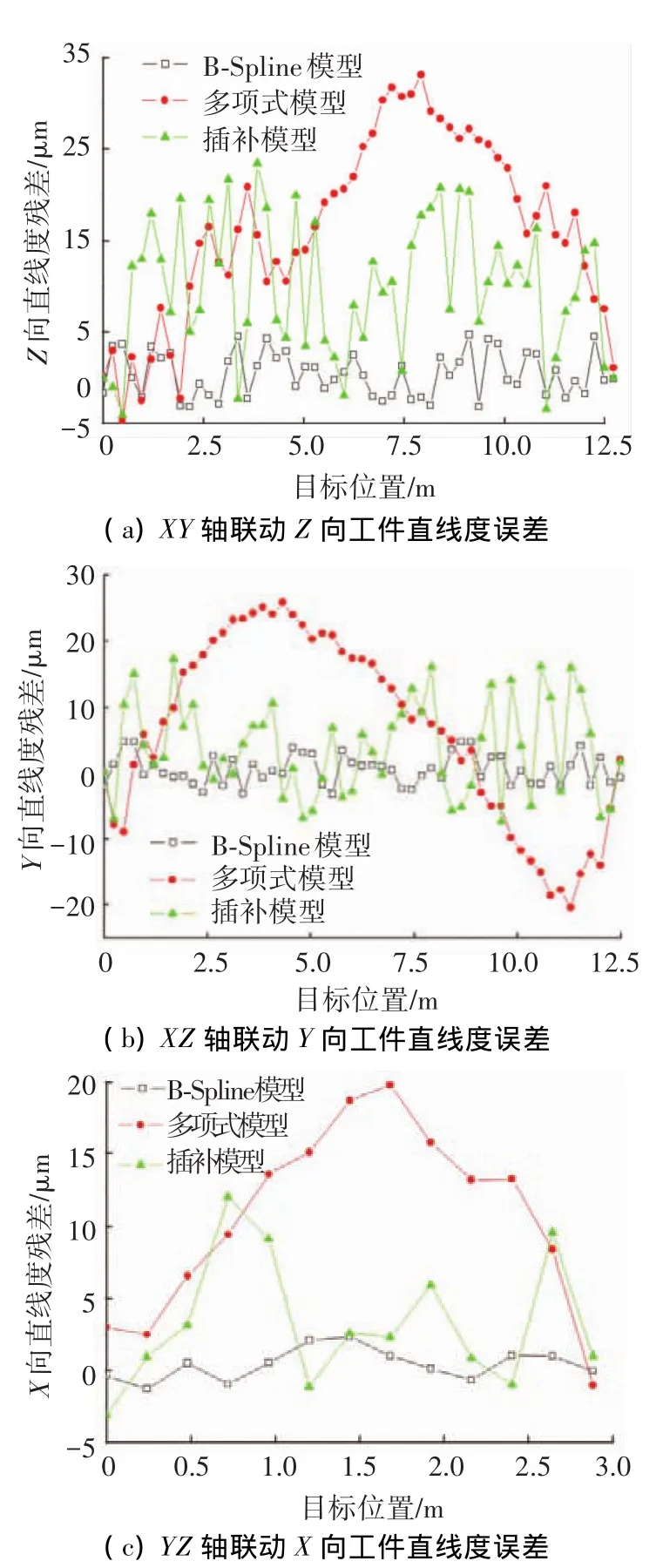
图10 空间运动切削后在X、Y、Z方向残差对比
B样条模型具有较高的建模精度,每4个点拟合一条曲线,各曲线之间柔性拼接,对速度和加速度的变化做了平稳过渡,避免了速度和加速度突变对机械带来冲击.B样条模型形状多变,具有拟合无规则数据的能力,具备了较高的建模精度,使用B样条模型具有较高的补偿精度,残差较小,具备了7次多项式模型和斜线插补模型的所有优点.
综上所述:B样条空间模型在实际切削情况下仍具有较高的预测精度,大范围减小加工误差,X方向直线度误差由41μm降低至3.6μm,Y方向直线度误差由91μm降低至8.0μm,Z方向的直线度误差由 160μm 降低至 7.9μm,机床加工精度提高90%以上.3个模型补偿后残差的具体对比结果如表1所示,表中B样条(Z),B样条(Y),B样条(X)分别表示B样条模型补偿后在Z、Y、X方向上的残差;7次多项式拟合(Z)、7次多项式拟合(Y)、7次多项式拟合(X)分别表示7次多项式模型补偿后在Z、Y、X方向上的残差;斜线插补(Z)、斜线插补(Y)、斜线插补(X)分别表示斜线插补模型补偿后在Z、Y、X方向上的残差.
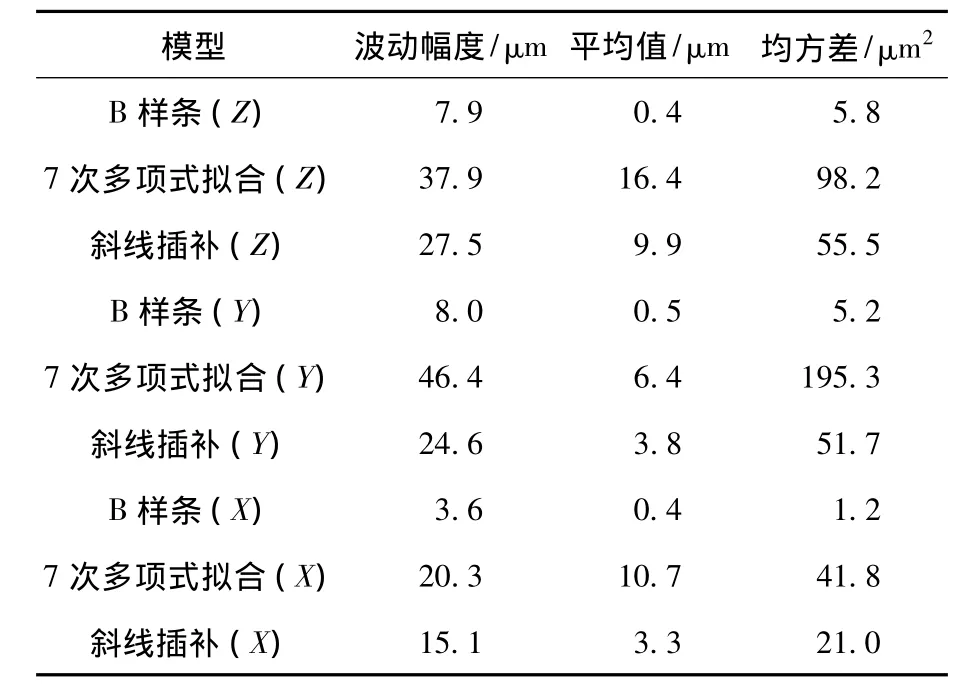
表1 3种模型补偿后残差对比
4 结论
1)利用Fanuc系统的外部机械原点偏移功能,采用实时补偿系统,依据空间直线度误差数学模型对龙门机床实施直线度误差补偿,加工精度提高均超过90%.
2)建立了基于B样条曲线的空间直线度误差数学模型,获得较高的建模精度.各方向直线度误差模型通过在空间矢量叠加得到该机床空间直线度误差数学模型,并通过两轴联动切削工件的方式验证了空间直线度误差数学模型的正确性.
3)与其他两种模型的补偿效果对比表明,B样条模型算法成熟,补偿精度高,鲁棒性好,适合于各种复杂的加工工况.补偿系统在长时间使用后,仍具有良好的补偿精度,至今还在某知名机床生产企业使用.
[1]HAN Zhenyu,JIN Hongyu,LIU Yulong,et al.A review of geometric error modeling and error detection for CNC machine tool[J].Applied Mechanics and Materials,2013,303/304/305/306:627-631.
[2] RAMESH R,MANNAN M A,POO A N.Error compensation in machine tools-a review PartⅠ:geometric,cutting-force induced and fixture-dependent errors[J].International Journal of Machine Tools and Manufacture,2000,40:1235-1256.
[3]贾立德,郑子文,李圣怡,等.使用短基准的超精密长导轨直线度误差测量方法[J].机械工程学报,2008(9):141-147.
[4]黄富贵,崔长彩.任意方向上直线度误差的评定新方法[J].机械工程学报,2008,44(7):221-224.
[5]ZHANG Qing,FAN K C,LI Zhu.Evaluation method for spatial straightness errors based on minimum zone condition[J].Precision Engineering,1999,23:264-272.
[6]黄富贵,崔长彩.评定直线度误差的最小二乘法与最小包容区域法精度之比较[J].光学精密工程,2007,15(6):889-893.
[7]唐浩.大型机床床身的加工[J].制造技术与机床,2007(8):106-107.
[8]尹德臻,邹雪巍.浅谈龙门磨床工作台导轨结构[J].机电产品开发与创新,2012(4):173-174,188.
[9] NI Jun.CNC machine accuracy enhancement through real-time error compensation [J]. Journal of Manufacturing Science and Engineering,Transactions of the ASME,1997,119(4):717-725.
[10]YANG Jianguo,YUAN Jingxia,NI Jun.Thermal error mode analysis and robust modeling for error compensation on a CNC turning center[J].International Journal of Machine Tools and Manufacture,1999,39(9):1367-1381.
[11]孟婥,车仁生.并联六坐标测量机的误差模型和误差补偿[J].哈尔滨工业大学学报,2004,36(3):317-320.
[12]CAO G,NAMBA Y.Straightness error compensation for ultra-precision machining based on a straightness gauge[J].Key Engineering Materials,2008,381/382:105-108.
[13]由凤玲,冯其波,张斌.基于共路光线漂移补偿的直线度测量[J].光学精密工程,2011(3):515-519.
[14]GAO W,ARAI Y,SHIBUYA A.Measurement of multidegree-of-freedom error motions of a precision linear airbearing stage[J].Precision Engineering,2006,30(1):96-103.
[15]姜辉,孙翰英,范嘉桢.基于FANUC 0i系统外部坐标原点偏移功能的数控机床误差补偿研究[J].机械制造,2009(7):73-76.
[16]LEI W T,SUNG M P.NURBS-based fast geometric error compensation forCNC machine tools [J].International Journal of Machine Tools and Manufacture,2008,48(3/4):307-319.
[17]HOSCHEK J,LASSER D.Fundamentals of computer aided geometric design[M].Wellesley:A K Peters,1993.
[18]PIEGL L,TILLER W.The NURBS book[M].New York:Springer,1995.
