一种点吸式波浪能装置水动力性能优化
2015-09-03王树齐
张 亮,国 威,王树齐
(哈尔滨工程大学船舶工程学院,150001哈尔滨)
波浪能作为一种清洁的可再生能源,蕴藏量巨大,为了缓解能源危机,波浪能装置的研发引发人们的日益关注.波能装置按结构形式分为点头鸭式[1]、振荡水柱式[2-3]、推摆式[4-5]、聚波蓄能式[6]、点吸式[7-9].点吸式波能装置有建造难度低、成本低、效率高等优点,已成为国内外学者研究的热点.平丽[10]基于线性势流理论,用边界元法研究装置的水动力性能,得出装置的俘获宽度比和最优阻尼的表达式,该方法忽略了流体的黏性效应.历福伟[11]利用ADINA软件建立了二维数值波浪水池,研究了浮子形状对振荡浮子式发电装置效率的影响.该方法的缺点是忽略了流体黏性,二维模拟仅限于形状简单的浮子,适用范围较窄.Guanche等[12]利用Simulink对一种波能装置进行了部分非线性时域数值模拟,通过改变电机的阻尼系数、装置直径、水深、轴承摩擦系数、垂向拖曳力系数、波高、周期等研究装置的水动力性能,此模型形状较为简单,没有对形状略复杂的浮子进行分析,不利于不同形状浮子水动力性能的对比.Vicente[13]对一种带有张紧锚链的点吸式波能装置的非线性水动力进行了时域和频域分析.Bhatta[14-15]等运用势流理论对处于有限水深的圆柱体的绕射和辐射问题进行了数学推导,并得出数值解,得到了圆柱体的在规则波中的运动规律.目前对点吸式波浪能装置的理论研究多以势流理论为主,装置中浮子形状过于简单,而且忽略了流体的黏性效应,与实际情况存在差异.
本文运用CFD方法,针对一种特定的点吸式波能装置进行三维数值模拟,对浮子形状及外界工作参数进行了优化分析.本方法的优势在于考虑了流体的黏性,可以对形状较为复杂的浮子进行计算,比势流理论更接近真实情况.
1 理论分析
1.1 浮子运动的数学模型
点吸式波能装置可简化为质量-弹簧-阻尼系统,浮子在波浪中垂荡运动时,受到惯性力、阻尼力、回复力和波浪力的作用,其中阻尼力与浮子垂荡速度成正比,回复力与浮子位移成正比.建立浮子的垂向受力平衡关系式:
式中:2ν为垂荡运动阻尼系数,2ν=(C+C0)/(m+λ);n为浮子垂荡固有频率,n2=(ρgs+K)/(m+λ);A为波幅;X0为波幅修正系数;ω为波浪频率;C为机械阻尼系数;C0为水的垂荡阻尼系数;m为浮子质量;K为弹性系数.
浮子垂荡的固有周期
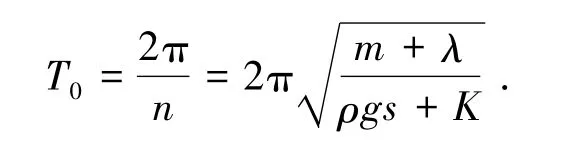
由式(1)得出浮子运动幅值z与波幅A的关系如下:
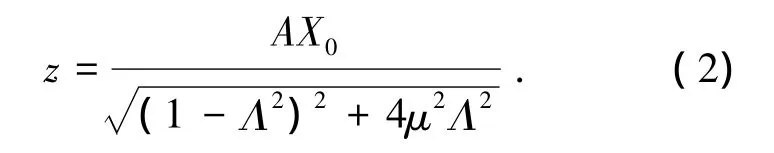
式中:Λ为波浪频率与浮子固有频率之比,Λ=ω/n;μ为无因次衰减系数.
入射波的功率Pi为浮子直径宽度内的波浪功率,且

式中:H为波高,T为波浪周期,D为浮子直径.浮子的平均吸收功率为

式中:FG为电机作用在浮子上的阻尼力,v为浮子垂荡速度,t2-t1=nT,n为整数.
浮子的俘获宽度比η定义为浮子平均输出功率与浮子宽度内波浪输入功率之比,即

浮子在做垂荡运动时对电机做功,通过电机的阻尼力转化为电能.
1.2 CFD数学模型
CFD方法基于黏性流体力学理论,采用基于有限元的有限体积法,在保证了有限体积法的守恒特性的基础上,吸收了有限元法的数值精确性,如式(6)和式(7)所示.
连续性方程:
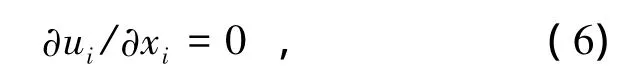
RANS方程组:

式中:ui和uj代表速度分量时均值,i,j=1,2,3;p为压力时均值;ρ为流体密度;ν为流体的运动黏性系数;gi为重力加速度分量为雷诺应力项.
针对本文的装置模型,选取合适的边界条件,采用动网格技术模拟浮体运动,采用体积分数法标记自由面,选取k-ω湍流模型,该湍流模型具有计算准确,收敛性好的特点,如式(8)和式(9):
k方程为

ω方程为

式中:k为湍动能,ω为湍流频率,Pk为湍流生成速率,β'=0.09,α=5/9,β=0.075.
2 数值计算
2.1 计算模型
运用ANSYS13.0中的CFX软件对浮子运动进行模拟,计算模型采用实体尺寸,如图1(a)所示,浮子上部为圆柱,下部为圆台,中间开孔.计算域的大小为50 m×20 m×50 m,采用推板造波,通过动网格模拟造波板运动,生成规则波[16],造波板、水池池壁、底部设置为No Slip Wall,水池顶部设置为Opening,水池尾部为消波区,可以大幅减少波浪反射.
计算域网格的划分如图1(b)所示,在波长方向对网格数量的控制取决于单位波长内的网格的数量,实践证明一个波长内应有120~150个网格,波高方向上30~50个网格,既保证了数值计算的精准度,又节省了计算时间.

图1 浮子尺寸及计算域网格示意
浮子位置距造波板15 m,浮子的运动求解采用刚体求解,约束其他自由度,使浮子仅做单自由度的垂荡运动,浮子力和运动的收敛标准取为10-4,计算时每个时间步的迭代次数在10~15次.时间步长为0.05 s,模拟10~15个波浪周期下浮子的运动.
2.2 有效性验证
为了验证CFD方法的有效性与准确性,分别采用商业CFD软件CFX和基于势流理论的计算软件AQWA对实验模型进行数值模拟,并与实验值对比,如图2所示.
实验模型的缩尺比为10,质量为14.25 kg,该实验在哈尔滨工程大学拖曳水池完成,实验波高为 0.08 m,周期为 2.2 s.
从图2中可以看出,运用CFD方法对浮子垂荡位移和速度的模拟结果与实验结果吻合良好,验证了CFD方法的有效性;将CFD值与势流理论值进行对比表明,CFD值比势流理论值更接近实验值,验证了该方法的准确性.综上可知,CFD方法对浮子运动的模拟有效且准确.
3 结果分析
波浪能装置的性能与很多因素相关,模拟浮子在不同形状、不同电机阻尼、不同质量下的运动,并分析得出了浮子在不同外界参数下的性能.
3.1 圆柱和圆台浮子的性能对比
计算分析两种形状的浮子在不用波况下的水动力性能,如图3所示,分为浮子在无负载和有负载下两种工况.
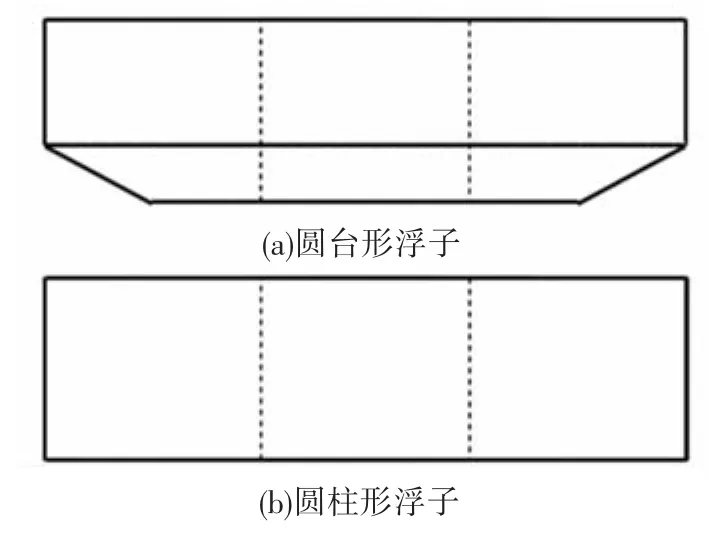
图3 圆台和圆柱形浮子形状示意
3.1.1 自然振荡
无负载时浮子在在波浪中做垂荡运动,此时浮子所受阻尼力来自于流体,装置阻尼系数仅为C0.式(2)说明了浮子的运动幅值与波幅的关系,将式(2)变形得
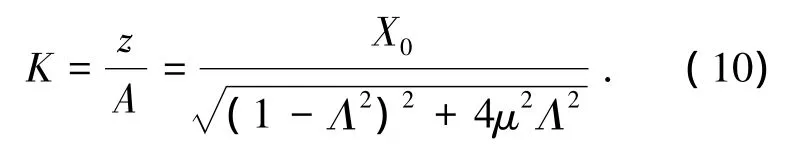
式中:K为放大系数,修正系数X0为1.
选取质量为17.528 t,直径和高度相同的圆柱和圆台进行对比,波高为0.4 m,波浪周期在2.40~5.06 s,如图 4 所示.
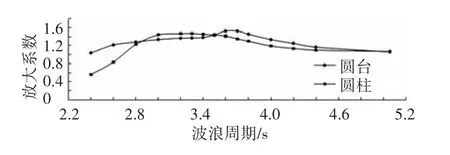
图4 圆台和圆柱在不同波浪周期下无机械阻尼时的幅值响应
从图4可以看出,随着波浪周期的增大,两者的运动幅值响应先增大后减小,原因如下:
根据式(10)可知,当浮子的固有周期大于波浪周期,即Λ>1时,浮子的运动受波浪影响很小,当波浪周期逐渐增大到Λ=1时,K出现最大值,此时浮子固有周期与波浪周期相同,发生共振,当波浪周期大于浮子固有周期即Λ<1时,浮子随波浪漂浮,波浪周期足够大时,浮子的运动幅值与波浪幅值相同,K趋近于1.
由于两种浮子的形状不同,其共振周期和K值都略有不同,圆台的共振周期为3.7 s,圆柱的共振周期为3.3 s,除圆柱的共振点附近的区域外,在波浪周期2.40~5.06 s范围内,圆台的运动幅值都高于圆柱,这说明同尺度、同质量的圆柱和圆台,圆台对波浪的响应要优于圆柱.
3.1.2 阻尼振荡
上述分析是圆柱和圆台浮子在无负载下做垂荡运动,装置在有外界机械阻尼时,阻尼系数增大,使无因次衰减系数μ增大,根据式(10)可知,浮子运动幅值将减少.图5为圆柱和圆台在机械阻尼为10 000 Ns/m时的幅值响应曲线.
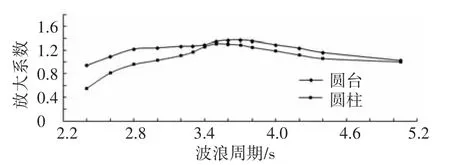
图5 圆台和圆柱在不同波浪周期下有机械阻尼时的幅值响应
从图5中可以看出,在相同波况下圆柱的运动幅值小于圆台,这是由于在波况相同时,圆台垂荡时作用于周围流体而产生的能量耗散小于圆柱,圆台自身剩余能量较大,其运动幅值也较大.从图中还可以得出圆柱的共振周期为3.5 s,而无阻尼时其共振周期为3.3 s,两者略有差异,这是由于浮子的共振与固有周期有关,固有周期的大小与浮子的附加质量有关,由于浮子在有阻尼和无阻尼时运动幅值不同,其周围流场存在差异,导致附加质量会有变化,从而影响其固有周期.
根据上述分析可知,在自然振荡和阻尼振荡时,圆台形浮子的垂荡运动性能要优于圆柱形浮子.
3.2 机械阻尼对浮子俘获宽度比的影响
圆台浮子运动性能较圆柱好,对圆台浮子进行模拟,选取波高为0.4 m,圆台浮子的共振周期为3.7 s的波况,浮子的质量和尺寸不变,对浮子在机械阻尼为10 000~200 000 Ns/m进行计算,图6(a)给出了浮子在机械阻尼系数为10 000、30 000和50 000 Ns/m下的运动曲线.
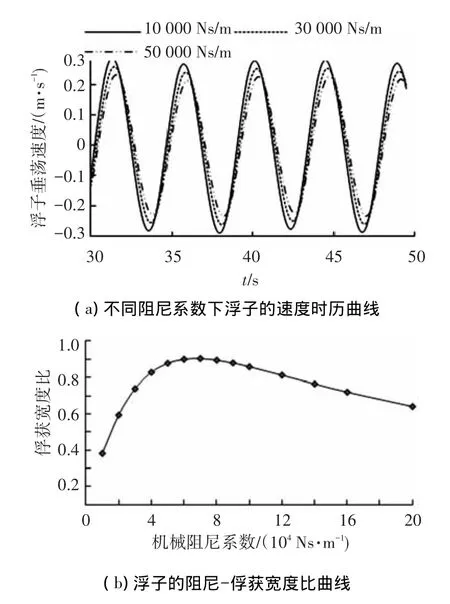
图6 不同阻尼系数下的浮子垂荡速度和俘获宽度比曲线
从图6(a)可以看出,在给定波况下,浮子的垂荡速度曲线趋于稳定后,其运动幅值基本保持不变,机械阻尼系数越大,浮子的速度幅值越小.通过分析可知,电机的阻尼系数为零时,浮子处于自由振荡状态,所受电机阻尼力为零,理论上浮子的输出功率为零;当电机阻尼系数无限大时,相当于浮子被刚性固定,速度为零,其输出功率也为零,因此找到最佳电机阻尼是必要的.图6(b)为不同阻尼系数下浮子俘获宽度比曲线,从图中可以看出,浮子的俘获宽度比随着机械阻尼的增大先增大后减小,在阻尼系数为70 000 Ns/m时,俘获宽度比达到最大值0.8.曲线先上升后下降的原因在于:根据式(3)~(5)可知,浮子宽度内的波浪功率与波高、周期和浮子直径有关,当浮子处于给定的波况时,波浪功率为定值,浮子俘获宽度比只与电机阻尼力和速度大小有关,浮子瞬时吸收功率为

由式(11)可知,浮子的瞬时吸收功率大小与阻尼系数和速度的平方成线性关系,而浮子的速度大小受电机阻尼系数的影响,浮子的运动速度随阻尼的增加而减少,阻尼越大,其克服外界阻尼力做功越多,导致其自身动能减少,速度就越小.总体表现为输出功率在某个速度上出现最大值.
3.3 质量对浮子俘获宽度比的影响
在对浮子形状和机械阻尼进行优化后,进一步计算圆台浮子质量对俘获宽度比的影响.选取波高为 0.4 m,周期为 4.4 s,机械阻尼系数为30 000 Ns/m,对不同质量的浮子进行计算.选取浮子质量范围为11~18 t,计算得出浮子质量-俘获宽度比曲线,如图7所示.

图7 浮子的质量-俘获宽度比曲线
图7中不同浮子质量对应不同的吃水,随着浮子质量的增加,其俘获宽度比先增大后缓慢减小,这是由于浮子质量增加后其吃水增加,使浮子所受波浪力对浮子做功增加,但随着吃水的继续增大会使浮子的惯性也相应增大,浮子对波浪的响应度降低,导致俘获宽度比略有下降.但在不同浮子质量的情况下,该波能装置的俘获宽度比浮动不超过2%.
由此可见,在远离浮子共振周期时,浮子质量的改变对装置的性能影响很小.在满足性能要求的基础上可适当减少浮子质量.
4 结论
1)相同尺度和质量的圆柱和圆台浮子的共振周期略有不同,自然振荡下的浮子的运动幅值要高于阻尼振荡时的运动;在两种振荡条件下,圆台浮子的运动性能优于圆柱浮子.
2)随着机械阻尼的增大,装置的俘获宽度比先增大后减小,表明装置存在最佳的机械阻尼,机械阻尼过大或过小都不利于浮子对能量的吸收.
3)质量的变化对俘获宽度比的影响不明显,考虑制造成本,可适当调节浮子质量.
4)基于CFD方法对浮子运动进行三维数值模拟,并对浮子在不同参数下的性能进行分析,得出最佳工况,实现了对该特定点吸式波能装置性能的优化.
[1]余志.海洋波浪能发电技术进展[J].海洋工程,1993,11(1):86-93.
[2]韩冰峰,褚金奎,熊叶胜,等.海洋波浪能研究进展[J].电网与清洁能源,2012,28(2):61-66.
[3]CLÉMENT A,MCCULLEN P,FALCO A.Wave energy in Europe:currentstatus and perpectives [J].Renewable& Sustainable Energy Reviews,2002(6):405-431.
[4]李允武.海洋能源开发[M].北京:海洋出版社,2008.
[5]CAMERON L,DOHERTY R,HENRY A,et al.Design of the next generation of the Oysterwave energy converter[C]//3rd International Conference on Ocean Energy.Bilbao:Amanda W,2010:22-39.
[6]任建莉,钟英杰,张雪梅,等.海洋波能发电的现状与前景[J].浙江工业大学学报,2006,34(1):69-73.
[7]ZURKINDEN A S,FERRI F,BEATTY S,et al.Nonlinear numerical modeling and experimental testing of a pointabsorberwave energy converter[J].Ocean Engineering,2014,78(1):11-21.
[8]SOREN R K,BISWAJIT B,MAHDI T,et al.Optimal control of an array of non-linear wave energy point converters[J].Ocean Engineering,2014,88(15):242-254.
[9]LOPES M F P,HALS J,MOAN T,et al.Experimental and numerical investigation of non-predictive phase-control strategies for a point-absorbing wave energy converter[J].Ocean Engineering,2009,36(5):386-402.
[10]平丽.振荡浮子式波能转换装置性能的研究[D].大连:大连理工大学,2005.
[11]历福伟.浮子形状对振荡浮子式波浪发电装置效率的影响[D].哈尔滨:哈尔滨工业大学,2011.
[12]GUANCHE R,GOMEZ V,VIDAL C,et al.Numerical analysis and performance optimization of a submerged wave energy point absorber[J].Ocean Engineering,2013,59(1):214-230.
[13]VICENTE P C.Nonlinear dynamics of a tightly moored point-absorberwave energy converter[J].Ocean Engineering,2013,59(1):20-36.
[14]BHATTA D D,RAHMAN M.On scattering and radiation problem for a cylinder in water of finite depth[J].International Journal of Engineering Science,2003,41(9):931-967.
[15] BHATTA D D. Computation ofhydrodynamic coefficients,displacement-amplitude ratios and forces for a floating cylinder due to wave diffraction and radiation[J].International Journal of Non-Linear Mechanics,2011,46(1):1027-1041.
[16]王永学.无反射造波数值波浪水槽[J].水动力学研究与进展,1994,9(2):205-214.
