混流式水轮机偏工况运行的大涡模拟方法验证

苏文涛，郑智颖，李小斌，李凤臣，兰朝凤，2

(1.哈尔滨工业大学能源科学与工程学院，150001哈尔滨;2.哈尔滨理工大学电气与电子工程学院，150080哈尔滨)

混流式水轮机在偏工况运行时，通常会出现内部流动不稳定，机组振动和噪声增大现象，除了固有的机械因素外，主要是由于流致振动造成，其中包括30%～60%额定负荷时尾水管涡带诱发大幅压力脉动，50%额定负荷时轮叶片进口Kármán涡脱流，这样不仅降低水轮机运行效率，严重时还会造成转轮相邻叶片中间区域出现叶道涡，并伴随空化现象［1］.偏工况运行中，在转轮区主要出现泡状或片状的翼型空化，空泡溃灭即为转轮破坏的主要因素.当转轮中至少有3个叶片表面出现气泡时，表明已经发生空化，转轮中空化程度主要由空化数σ来描述.实验证明，水轮机压力脉动的强度随空化数的减小而迅速提高，而运行效率则随之下降［2］.针对混流式水轮机中内部的不稳定流动和空化现象，众多学者展开了实验研究和数值模拟研究.实验研究主要针对水轮机流道的各个部分，采用粒子图像测速仪(PIV)来进行流场的测量和分析.Iliescu等［3］采用 PIV技术对混流式水轮机尾水管内汽、液两相流动进行测量，研究空化尾水管涡带结构.Palafox 等［4］和 Uzol等［5］分别采用PIV实验研究了轴流式水轮机叶顶间隙内的湍流流动，该轴流式水轮机比转速较低，且叶顶泄漏较为复杂，在下游将形成二次流.Katz等［6-7］基于对轴流式水轮机的PIV测量结果，引入湍动能组分平衡的观点，分析了叶顶间隙流动及其尾迹的流动特征.针对偏工况运行时的混流式水轮机尾水管内流动，李丹等［8］、王军等［9］和陈次昌等［10］对其二维流场和涡带运动特征展开了研究，分析涡带的周期性运动特征.实验研究已经揭示了水轮机内复杂流场的形成原因及其与流场边界之间的作用结果;然而，由于三维流动伴随空化这一现象的复杂性，目前在众多发生流动空化的场合中，实验研究仍存在很多困难.如导叶之间与转轮叶片之间的流场测试十分复杂，对于具有复杂三维流场的水轮机，采用数值模拟方法研究空化非定常流动成为观测空化现象发展的重要技术.

对大型混流式水轮机机组内部空化流动数值研究的主要目的是从宏观和微观两方面揭示流动稳定性问题.目前，对于叶片式流体机械内部流场的数值计算，仍以雷诺平均数值模拟(RANS)方法为主，而该方法中雷诺应力基于线性模型计算，使某些包含细节信息的高频分量被滤除，数值模拟不能体现真实的多尺度湍流流动.大涡模拟(LES)的思想是将小尺度的涡从流动中分离出来，通过小尺度涡和大尺度涡之间的相互影响来描述不同尺度涡结构的相互作用.数学表达上，可在大涡流场的运动控制方程中添加相应的附加应力项来体现小涡的影响，该附加应力项即为亚格子(SGS)应力项.一般认为湍流中小尺度涡的结构趋于各向同性，基于不同涡特征即可构造不同的SGS模型.在水轮机数值模拟方面，Zhang等［11］对某一混流式水轮机进行了三维LES，并将计算结果与压感片实验获得的结果作了比较，得到了令人满意的结果，但其研究仅限于叶片部位;Liu等［12］采用LES研究了混流式水轮机尾水管涡带的形态，通过对比不同负荷下的涡带形态，发现越偏离设计工况，漩涡强度越大;黄剑峰等［13］使用LES动态亚格子湍流模型和先进的滑移网格技术对混流式水轮机全流道动静干涉的三维非定常湍流场进行了动态LES，计算结果表明LES对复杂流场的仿真效果更加准确.针对上游尾迹对入口流动的扰动，Wang等［14］对某一混流式水轮机的单流道模型进行了LES模拟，发现强尾迹将造成叶片前缘处的大面积流动分离，并沿展向形成主涡.Ma等［15］采用混流式水轮机单流道模型，验证了LES中SGS模型对计算结果的影响，并和实验进行了对比，发现适应壁面的涡黏模型和实验结果符合最好.而最近，RANS-LES混合湍流模型也被逐渐应用在水轮机模拟中［16-17］，较好的模拟结果体现了LES自身特性带来的优势.

由于水轮机全流道的几何复杂性，上、下游部件之间流动干扰，以及旋转部件与静止部件之间的流动干涉，使全流道计算及分析相对困难;另外，由于空化的产生是由于液体在低压区发生相变，如何准确地捕捉到空化区域也成为了必要问题.目前，对于水轮机的数值研究，很少进行全特性验证.本文用LES方法，并结合空化模型，对某一大型混流式水轮机在不同活动导叶开度下的特性及在不同工况点的空化流场进行全通道三维数值计算，对比分析单相流与空化两相流计算结果，并对外特性和内流场进行实验结果对比，验证针对偏工况运行的混流式水轮机的基于空化模型的大涡模拟方法.

1 计算模型与数值模拟方法

1.1 水轮机模型与几何参数

对某大型混流式水轮机的模型进行数值模拟，几何模型如图1所示.从流动入口到流动出口依次分为蜗壳、固定导叶、活动导叶、转轮及尾水管5个通道部件，其中入口段前面增加了直管段部分，用来稳定蜗壳的入口流动状态.该模型的具体几何参数参见表1.

表1 模型水轮机基本几何参数

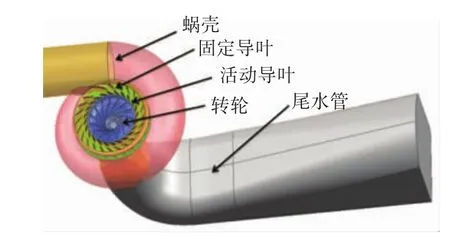
图1 混流式水轮机几何模型

1.2 控制方程

采用LES方法(Smagorinsky-Lilly模型)对混流式水轮机内部流动进行数值模拟计算.对不可压缩牛顿流体流动，用过滤算子对Navier-Stokes方程进行变量过滤，可得基于LES的动量守恒方程为

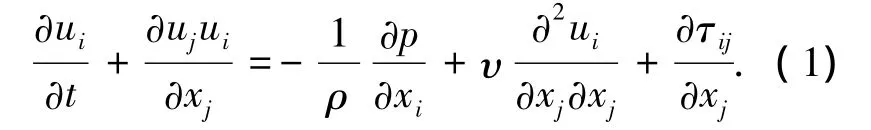
式中:ui为i方向流动速度，xi为笛卡尔坐标系下x、y、z3 个分量，p为压力，ρ为流体的密度，υ为流体的运动黏度，τij为SGS应力项.

采用Smagorinsky-Lilly模型有

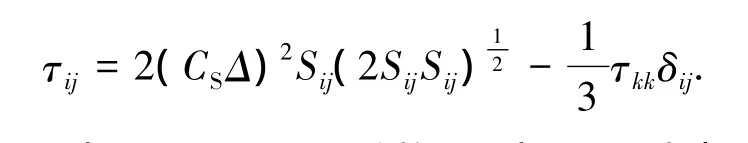
其中CS为Smagorinsky系数，Δ为LES过滤尺度，Sij为可解尺度的变形率张量，δij为克罗内克符号.Smagorinsky-Lilly模型中，SGS应力可表述为

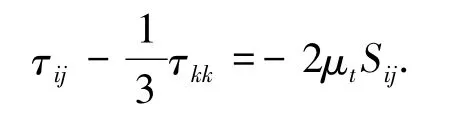
式中，涡黏性μt为亚格子尺度的湍动黏度.

Smagorinsky常数CS可根据Kolmogorov常数CK获得:

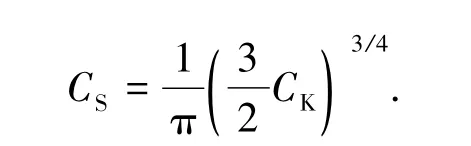
通常为减小SGS应力的扩散，提高计算过程收敛性，特别是在近壁区，CS取值可适当减小.考虑到全通道中壁面对流动的强烈作用，在近壁区可以按照 Van Driest模型来修正CS值［18］，即

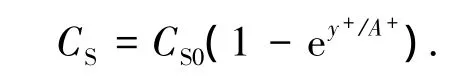
其中y+为网格节点到壁面的量纲一的距离，参数A+=25，CS0=0.1.

为更准确模拟空化流动的发生情况，计算中除使用单相流动模型之外，还引入了描述空泡运动的空化模型.商业CFD软件ANSYS中目前已经集成了基于Rayleigh-Plesset方程的几种空化模型，如 Singhal模型、Schnerr-Sauer模型和 Zwart-Gerber-Belamri(ZGB)模型［19］，这几种模型均描述了空化过程中的相变，考虑了流场中空泡的密度变化与其运动特征的联系.薛瑞等［20］和刘厚林等［21］针对不同的湍流场，对3种空化模型进行了比较研究，发现ZGB模型的计算收敛性较佳，计算稳定.故文中计算选用ZGB空化模型.

1.3 网格划分与边界条件

根据水轮机的几何模型，依次按照蜗壳、固定导叶、活动导叶、转轮、尾水管5个部分分别划分网格，然后组合为模型水轮机的全流道网格，其中在相邻部件之间，均设置了网格交界面(interface).网格划分的最终结果如图2所示，针对具有翼型结构的导叶和转轮部件，在其近壁面处均进行了边界层网格加密，以满足壁面流动计算的要求.

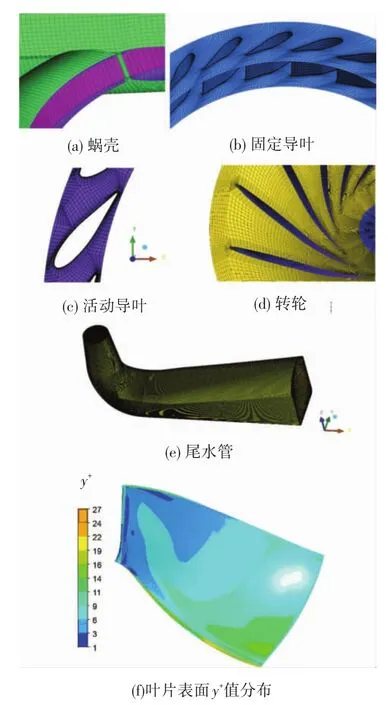
图2 网格划分细节图

对计算结果进行网格无关性验证，选定设计工况对不同节点数的网格进行了模拟验证，通常无关性验证以模型实验效率为标准，以核对数值计算得到的水力效率.该计算工况下，活动导叶开度a=18 mm、单位转速n11=60.6 r/min(即最优工况)，模型实验效率为η=94.8%.计算发现，在网格数超过一定数量后，随网格节点数目的增加，计算得到的水轮机水力效率值趋于稳定，并和模型实验的效率相吻合，故当计算域网格数量达到829万时即可满足要求.该工况下叶片表面的y+值见图2，可以看出，y+值符合大涡模拟的计算要求.水轮机各个部件的网格参数如表2所示.

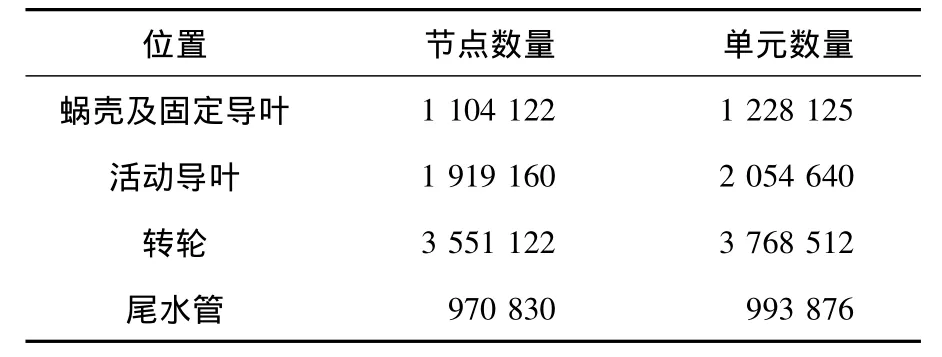
表2 计算域网格结点数及单元数

边界条件设置中，流动入口设置为计算域进口(蜗壳前直管段);采用总压进口条件，该值通过模型实验中所采用的水头和进口水流速度来给定;流动出口设置为尾水管的出口，采用压力出口;体壁面均采用无滑移边界条件.

1.4 求解方法

选取ANSYS中的CFX求解器进行水轮机内部全流道三维模拟计算.针对旋转部件(转轮)与静止部件(活动导叶出口、尾水管进口)的交界面，坐标变换模型均采用瞬态动静干涉(Transient Rotor-Stator)模式.对流项离散格式选用 High resolution格式，同时计算的每个时间步长中保证转轮旋转1°，计算迭代100次，收敛的残差标准为1×10-5.考虑到流场中近壁区的局部低雷诺数性质，在LES求解中，近壁区的流动采用标准的壁面函数来处理.

2 计算结果及分析

数值模拟中，选取与Su等［22］的实验测量相同的流动工况，即在偏离最优导叶开度a=18 mm的两条活动导叶开度线a=10 mm和a=14 mm上，分别选取5个工况点进行LES(单相流和空化流动)计算，具体计算工况分布如表3所示.

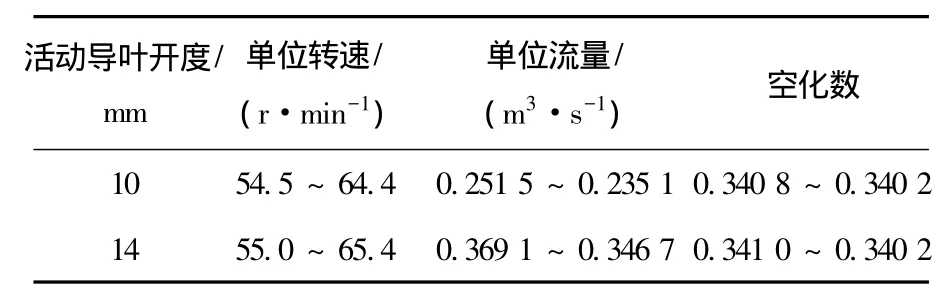
表3 计算工况点参数

2.1 内流场和外特性验证

为对比LES与RANS对混流式水轮机内部流场和空化性能预测的精度，Su等［23］对某一偏工况下的流场进行了三维全通道单相流LES，结果表明，LES比RANS能很好地再现流场中的空化涡.为了描述水轮机内部流场的特征，下面给出对活动导叶开度14 mm时单位转速为65.4 r/min、单位流量为0.346 7 m3/s的计算结果，计算启用空化模型，即为多相流LES计算，并将结果和未启用的空化模型的单相LES进行比较.

图3为两种计算方法对无叶区附近流场的预测情况，选取沿导叶高度方向的中间平面，并以靠近固定导叶侧的测量线端点为x轴起始点，图中给出了基于平均速度场的流线及该测量线上量纲一的速度U/U0分布，其中U为当地绝对速度，U0为根据蜗壳进口流量计算得到的平均速度.

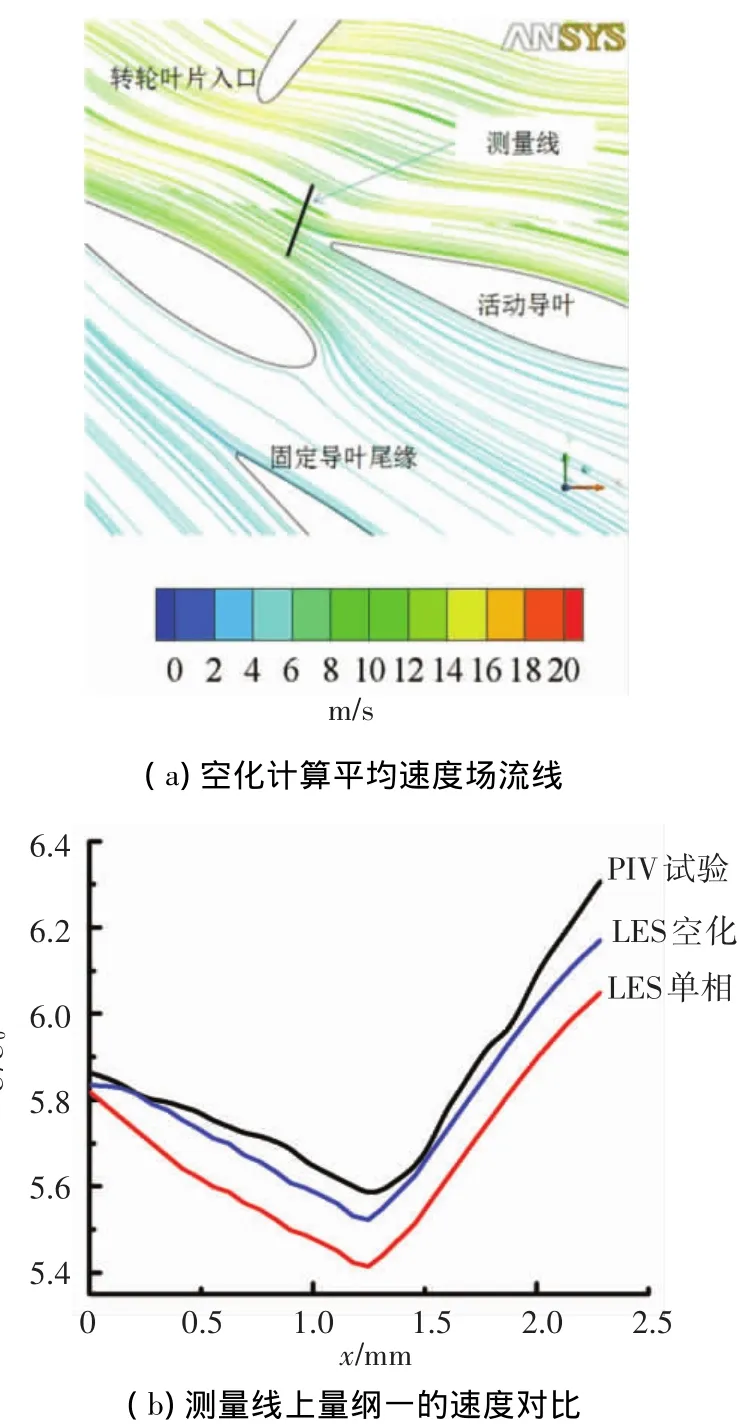
图3 无叶区流场数值模拟与实验结果对比(a=14 mm)

定量分析表明，活动导叶之后的尾迹流动在导叶压力面一侧(转轮侧)流速较高，而在吸力面一侧(固定导叶侧)流速较低，这是翼型扰流的显著特征.通过对比文献［22］中PIV实验的流场分布，发现两种方法获得的活动导叶尾迹平均流场流线走势与PIV实验结果一致，LES空化计算获得的测量线上速度值的大小与PIV实验获得的结果符合得更好.

图4给出了不同活动导叶开度下LES计算结果与实验结果的对比，包含了启用和未启用空化模型时的情况.可见，单位转速与单位流量的关系与模型实验符合很好，表明采用空化计算的LES能够很好地预测水轮机模型的外特性，图4(b)中活动导叶开度a=18 mm的计算结果作为对比.从图4(a)和(b)可以看出，采用空化两相LES计算的结果与实验更加吻合，而单相LES的计算结果与实验值有些许偏离.在上述工况下，同一开度下的水轮机单位流速与单位流量曲线接近线性变化关系，且3个开度下的特性曲线基本平行，即该范围内，水轮机运行时的实际转速与全流道内流量也应成线性关系.

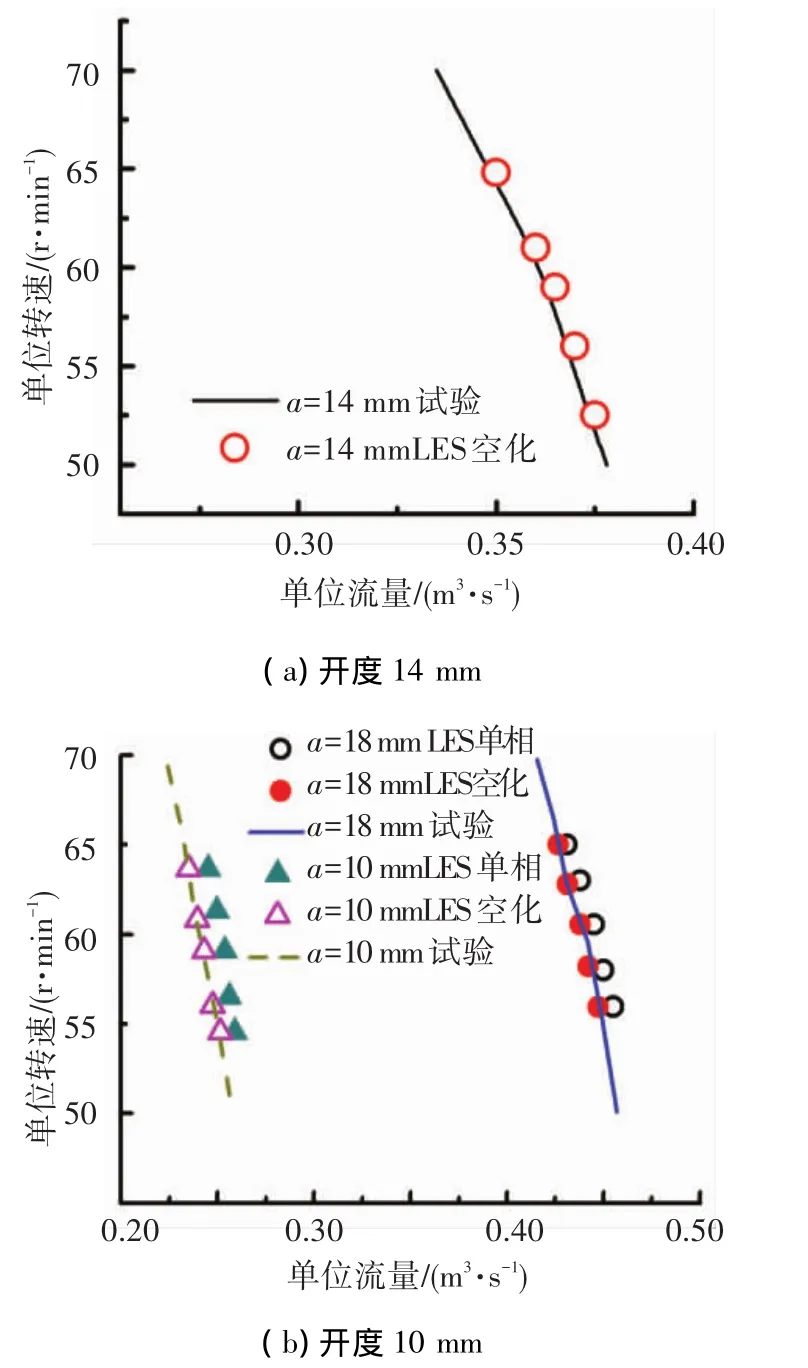
图4 不同活动导叶开度下的外特性对比

图5给出了活动导叶开度a=10 mm时通过空化LES空化计算水轮机中真实流量-转速(Q～N)与效率 -转速(η-N)的关系曲线，其中a=18 mm的计算结果作为对比.由于在水头不变的情况下，流动中n11与N成线性变化关系，图5的结果也同时验证了图4的结论，即在上述工况变化范围中，n11～Q11与Q～N均呈现线性关系.额定工况下，计算得混流式水轮机的水力效率接近95%，且水力效率随着转轮转速的降低而减小.当转速N＜800 r/min时，η迅速下降.在小开度a=10 mm工况，水力效率下降较小，但运行效率总体较低，约87%左右.

为了验证空化LES对运行效率计算的准确程度，图6给出了效率曲线与模型水轮机实验获得综合特性曲线的对比.图中数据点来自于图5，且将实际转轮转速转换成了单位转速.

图6中，计算得到的效率点(η，n11)由圆圈标示，圆圈中心标示了效率点的位置.可以看出，效率点均非常接近于模型实验的开度线a=10 mm和a=18 mm，即空化计算的效率曲线与综合特性曲线相符合.另外，对比模型综合特性曲线可知，设计工况处效率曲线陡峭，而偏工况时，效率曲线比较平缓.可见，启用空化模型的LES可以很好地再现并预测水轮机的外特性.

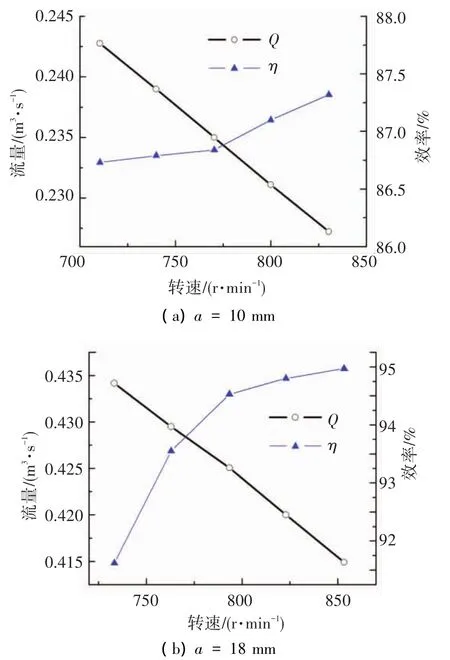
图5 不同活动导叶开度下空化两相流计算的转速－流量与转速－效率曲线

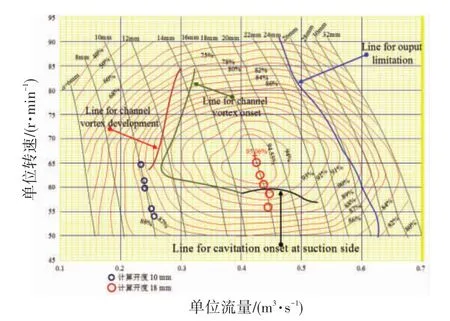
图6 使用空化LES计算得到不同开度下效率曲线与综合特性曲线对比图

2.2 叶道涡预测及其演化

叶道涡是转轮内部发生空化之后形成的涡结构，其溃灭时会对叶片表面产生严重的侵蚀，所以准确预测叶道涡的生成与发展对水轮机正常运转具有重要意义.为了对叶道涡形态进行可视化，ANSYS软件提供了许多涡结构特征提取方法，如螺旋度(Helicity)方法、涡流强度(Swirling strength)方法、涡量(Vorticity)方法、Q方法和λ2方法等.

用涡量准则显示转轮区的涡量分布.通过给定涡量的阈值，涡量准则可以正确判定出漩涡存在的区域，下面分别对启用和不启用空化模型时的工况进行分析.针对活动导叶开度a=10 mm、n11=59.9 r/min工况，先分别计算出空化LES和单相LES模拟结果的平均速度场，再采用0.5倍平均涡量 ＜|Ω|＞作为阈值进行叶道涡显示，如图7所示.可以看出，空化LES可以捕捉到更多的叶道涡，且更加符合模型实验获得的叶道涡形态［22］;但单相LES则不能很好地捕捉到沿流向的叶道涡运动.

图7 平均流场的叶道涡可视化

针对叶道涡的演化过程，下面将进一步对涡结构的变化进行说明.如图8所示，计算工况为活动导叶开度14 mm，单位转速61.0 r/min，进行空化LES计算.

图8 空化LES计算获得的叶道涡演化过程

图8中给出了水轮机转轮内部叶道涡生成、发展和溃灭的一个典型演化过程，空化涡使用Q方法进行提取，并和相同工况下的模型实验进行了比较.可见，叶道涡位于叶片通道之间，并初生于叶片进水边附近，随时间变化，转轮顺时针旋转，空化涡体积逐渐增长(1～3)，达到最大之后，又逐渐减小直到消失(4～5).需要注意的是，从1～5，在叶片的出水边(模型实验未监测叶片出水边)附近，有大量空化涡沿着展向分布，这是由于叶道涡在不断生成积累过程中，随主流流动而被带到了出水边.部分空化涡将被进一步带到流动通道的下游，在尾水管中形成碎涡结构.

文献［22］已通过实验发现，转轮在偏工况下运行时，其中叶道涡的变化呈现高频特征，且其演化频率为转频的整数倍，该倍数一般为转轮叶片数.在上述计算中，设置时间步长为转轮每转动1°的时间，可以得到叶道涡变化的一个周期为转轮转动 24°，对应时间为 0.005 2 s，约 192.31 Hz.而该流动条件下，单位转速为61.0 r/min，转轮实际转速 757.8 r/min，故转频为 12.63 Hz，可见叶道涡演化的周期正好约为转频的15倍，和叶片数相同.于是，上述数值模拟的结果和模型实验的结果相符合，即使用空化LES计算能够很好地预测水轮机偏工况运行时的叶道涡运动.

2.3 尾水管涡带演化

尾水管涡带是水轮机中另一种空化现象，从转轮出口的中心开始，向肘管发展.由于转轮出口水流的周期性运动，该涡带也在不断旋转运动，随不同工况的变化涡带具有不同的形态，其运动会引发尾水管壁面的周期性压力脉动.

针对活动叶开度10 mm、单位转速64.9 r/min工况分别使用空化LES和单相LES计算，提取尾水管中空化涡带结构，如图9所示.将25℃下水的汽化压力作为等值面提取涡形态，可见，空化LES计算得到的涡带形态与模型实验观测到的结果接近，该工况下尾水管涡带呈现螺旋状.另外在该工况下单相LES出现了分岔的涡带形态，说明单相流计算不能很好地处理气液密度变化和压力变化的关系，而空化两相流则考虑了空泡密度与流场运动的关系，故能获得较为满意的空化形态.

为了获取尾水涡带的演化过程，对活动导叶开度14 mm、单位转速61.0 r/min的工况进行空化LES计算，如图10所示.图中显示为从尾水管开始的锥管段涡带部分，事实上涡带发展是从转轮下方的泄水锥开始，为了显示清楚涡带的旋转情况，特意截取尾水管中的一段空化涡带.图10表征了尾水管涡带旋转一周的演化过程，其所用时间约为转轮旋转2.5周的时间，可见，涡带的演化是一个低频过程，即约为转频的0.4倍，和文献［22］的结论相符合.

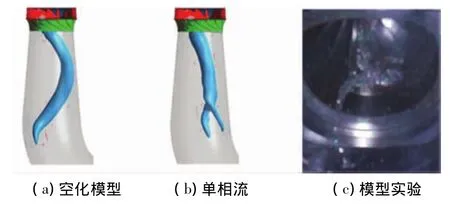
图9 尾水管涡带形态对比

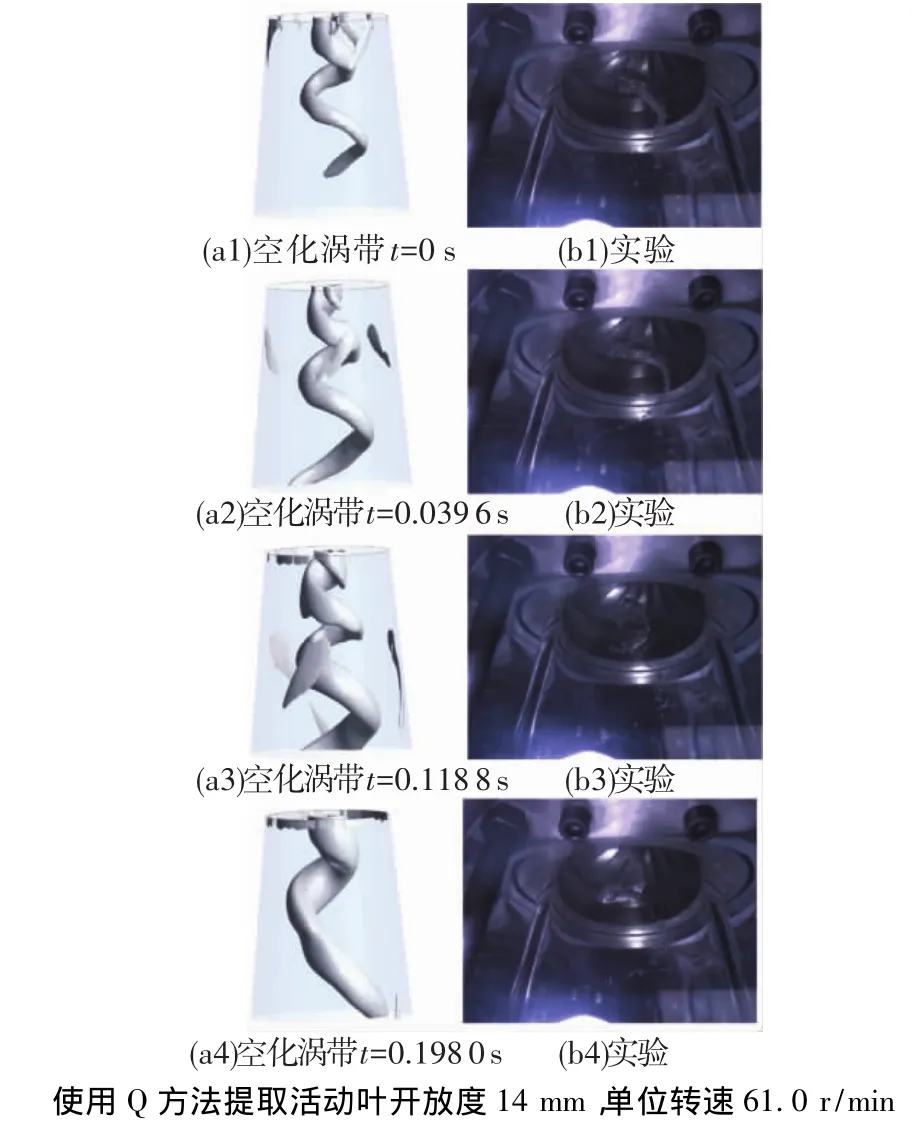
图10 空化LES计算获得的空化涡带演化过程

由形态结构可看出，从泄水锥生成的空化涡被携带到下游时，会随着转轮的旋转而变成螺旋状结构，并不断增长，获得的空化涡结构和模型实验比较符合.而中心涡带在增长的同时，在接近尾水管壁面的部分有破碎涡生成，可以推测，部分破碎涡来源于转轮出水边集结的空化涡.这些破碎涡在涡带旋转一周的时间中，将从下游的肘管处泻出，之后，涡带形态将开始下一个周期变化.从机理上看，由于空化LES计算特别考虑了空化区域的压力、密度变化和流场运动的关系，故能更好地处理流场中压力梯度变化剧烈的区域.可见通过LES可以预测尾水管入口处压力梯度较高的区域，和实际流动情况相符合.

综上所述，采用空化模型的LES不仅可以准确地获得混流式水轮机内部三维流场，更能很好地捕捉到空化区域的形态特征，尤其针对叶道涡和尾水管涡带的形态演化，对水轮机的稳定运行具有重要的意义.

3 结论

1)LES可以预测尾水管入口存在压力梯度较高的区域，且能捕捉到尾水管锥管段复杂的涡带旋转流动，而RANS则不能准确预测.

2)采用空化两相流LES计算的外特性结果与实验对比吻合度高，而单相流计算结果与实验值偏差较大.

3)采用空化两相流的LES可以很好地捕捉到转轮叶片之间沿流向发展的叶道涡，与实验结果相吻合，验证了基于空化模型的LES方法在预测偏工况下混流式水轮机性能的可行性与准确性.

4)空化LES获得的叶道涡演化过程为高频运动，而尾水管涡带为低频运动，和模型实验结果相符合.

［1］DÖRFLER P，SICK M，COUTU A.Flow-induced pulsation and vibration in hydroelectric machinery［M］.London:Springer，2013.

［2］WEI X Z，SU W T，LI X B，et al.Effect of blade perforation on Francis hydro-turbine cavitation characteristics ［J］.Journal of Hydraulic Research，2014，52(3):412-420.

［3］ILIESCU M S，CIOCAN G D，AVELLAN F.Analysis of the cavitating draft tube vortex in a francis turbine using particle image velocimetry measurements in two-phase flow［J］.ASME Journal of Fluid Engineering，2008，130:21105.

［4］PALAFOX P，OIDFIELD M L G，LAGRAFF J E，et al.PIV maps of tip leakage and secondary flow fields on a low-speed turbine blade cascade with moving end wall［J］.Physics of Fluids，2008，130:11001.

［5］UZOL O，CHOW Y C，KATZ J，et al.Average passage flow field and deterministic stresses in the tip and hub regions of a multistage turbomachine［J］.Experiments in Fluids，2003，125(4):714-725.

［6］ UZOL O，KATZ J.Flow measurement techniques in turbomachinery［M］//Handbook of Experimental Fluids Mechanics.Heidelberg:Springer，2007:917-957.

［7］KATZ J，CHOW Y C，SORANNA F，et al.Experimental Characterization of Flow Structure and Turbulence in Turbomachines［C］//5th International Symposium on Fluid Machinery and Fluids Engineering.Jeju:［s.n.］，2012.

［8］李丹，陈次昌，季全凯，等.PIV测试水轮机尾水管锥管流场［J］.西华大学学报:自然科学版，2004(S1):228-230.

［9］王军，付之跃，温国珍，等.HL220改型装置不同工况下尾水管进口流动状态PIV试验研究［J］.工程热物理学报，2005，26(S1):93-96.

［10］陈次昌，李丹，季全凯，等.混流式水轮机尾水管内部流场的 PIV测试［J］.机械工程学报，2006，42(12):83-88.

［11］ZHANG L X，GUO Y K，WANG W Q.Large eddy simulation of turbulent flow in atrue 3D francis hydroturbine passage with dynamicalfluid-structure interaction［J］.International Journal for Numerical Methods in Fluids，2007，54(5):517-541.

［12］LIU X B，ZENG Y Z，CAO S Y.Numerical prediction of vortex flow in hydraulic turbine draft tube for LES［J］.Journal of Hydrodynamics，Series B，2005，17(4):448-454.

［13］黄剑峰，张立翔，王文全.混流式水轮机全流道三维非定常湍流场的动态大涡模拟［J］.中国农村水利水电，2009(1):101-108.

［14］WANG W Q，ZHANG L X，YAN Y.Large-eddy simulation of turbulent flow considering inflow wakes in a Francis turbine blade passage［J］.Journal of Hydrodynamics，Series B，2007，19(2):201-209.

［15］MA J M，WANG F J，TANG X L.Comparison of several subgrid-scale models for large-eddy simulation of turbulentflows in water turbine［C］//The 4thInternational Symposium on Fluid Machinery and Fluid Engineering.Beijing:［s.n.］，2008.

［16］NETO A D A，JESTER-ZUERKER J，JUNG A，et al.Evaluation of a Francis turbine draft tube flow at part load using hybrid RANS-LES turbulence modelling［J］.IOP Conf Series:Earth and Environmental Science，2012(15):062010.

［17］SENTYABOV A V，GAVRILOV A A，DEKTEREV A A，et al.Numerical investigation of the vortex core precession in a model hydro turbine with the aid of hybrid methods for computation of turbulent flows［J］.Thermophysics and Aeromechanics，2014， 21(6):707-718.

［18］王福军.计算流体动力学分析:CFD软件原理与应用［M］.北京:清华大学出版社，2004.

［19］ZWART P J，GERBER A G，BELAMRI T.A twophase flow model for predicting cavitation dynamics［C］//Fifth International Conference on Multiphase Flow.Yokohama:ICMF COP，2004:No.152.

［20］薛瑞，张淼，许战军，等.对不同空化模型的比较研究［J］.西北水电，2014(2):85-89.

［21］刘厚林，刘东喜，王勇，等.三种空化模型在离心泵空化流计算中的应用评价［J］.农业工程学报，2012，28(16):54-59.

［22］SU W T，LI X B，LI F C，et al.Experimental investigation on the characteristics of hydrodynamic stabilities in Francis hydro-turbine models［J］.Advances in Mechanical Engineering，2014，Article ID 486821.

［23］SU W T，LI F C，LI X B，et al.Assessment of LES performance in simulating complex 3D flows in turbomachines ［J］. Engineering Applications of ComputationalFluid Mechanics， 2012， 6(3):355-364.