回转窑托轮辐板结构的力学依据Mechanics Basis for Spokes Board Structu reofRotary Kiln Suporting
2015-09-01江旭昌
江旭昌
回转窑托轮辐板结构的力学依据
Mechanics Basis for Spokes Board Structu reofRotary Kiln Suporting
江旭昌
托轮是回转窑的重要机件之一,一般由各种铸钢制成。托轮通过轮带承担回转窑(包括自身筒体、窑衬和物料等)整个回转部分的重力,负荷较大,常常发生不同形式的破坏而报废。由于托轮与托轮轴的联接基本上采用热装或称红装方式,无法拆卸,所以当托轮报废时托轮轴也随之报废,使企业遭受叠加损失。
回转窑托轮主要由轮缘、辐板和轮毂三部分构成。在20世纪80年代以前,国内外的回转窑托轮均采用带有真正辐板的结构。为了清砂,在辐板上必须设有沿圆周均匀分布的数个呈椭圆形或圆形等不同形状的铸孔,将其称为“清砂孔”。托轮的破坏失效形式主要表现为与轮带接触表面的磨损、掉渣掉块和出现裂纹甚至裂断。对于采用真正辐板结构的传统托轮,主要的破坏形式是辐板清砂孔的断裂。在使用中发现,采用长轴沿托轮径向分布的椭圆形清砂孔,即使轮缘磨薄二分之一也不会发生断裂(图1)。而采用短轴沿托轮径向布置的椭圆形清砂孔,发生断裂的情况则屡见不鲜,且基本上始发于椭圆孔长轴的两端,不少水泥厂因采用这种清砂孔断裂而报废的托轮堆积如山(图2),严重地影响了回转窑的运转率,损失很大。为解决这个问题,笔者受有关厂家的委托,对这种破坏现象进行了力学理论分析。
当代的回转窑托轮国内外都进行了很大改进,基本上淘汰了带有真正辐板式的传统托轮结构,而采用近于“死托轮”的结构。然而,这些改进的基础仍源自对传统托轮辐板清砂孔的理论分析,起辐板作用的结构仍然保留着各种不同形状的铸孔或加工出起吊孔。前述理论分析对研究托轮辐板结构或其他带有不同孔形的板件强度仍然具有理论指导意义,对现在仍使用带有辐板的传统托轮理论指导意义更大。
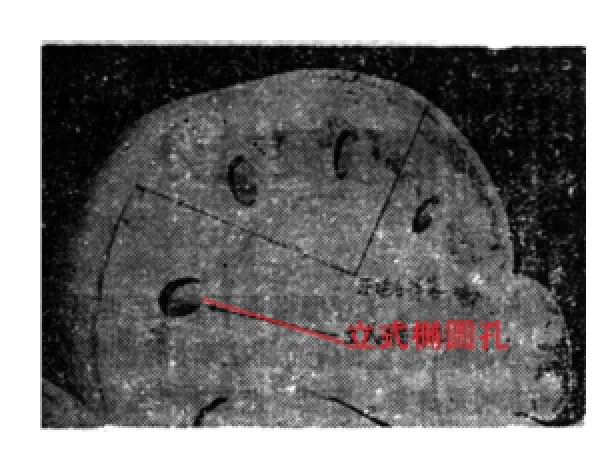
图1 长轴径向布置椭圆形清砂孔的托轮

图2 某水泥厂φ4m×60m立波尔回转窑报废的托轮
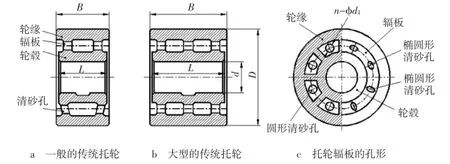
图3 传统托轮辐板清砂孔的形状
1 传统托轮和近代托轮的结构特点
铸有明显辐板结构的托轮称为“传统托轮”,轮缘、辐板和轮毂界限特别清楚,如图3所示。为了清砂,辐板上都铸出清砂孔。清砂孔的形状基本上有三种,即长轴沿托轮径向布置的椭圆形清砂孔、短轴沿托轮径向布置的椭圆形清砂孔和圆形清砂孔。较早国内设计的回转窑托轮,采用短轴沿托轮径向布置的辐板椭圆形清砂孔最多,因此断裂的也最多。采用圆形清砂孔的托轮,只有在较小的窑上才能见到。
改进后的托轮均采用近于“死托轮”的结构,已没有明显的辐板存在,这些不同型式的托轮称为“近代托轮”,如图4所示。图4a所示为德国洪堡公司的“死托轮”结构,与图4b所示美国富乐公司的“死托轮”结构相同,都钻制有两个起吊圆孔。图4c是丹麦史密斯公司的近代托轮结构,我国柳州水泥厂3 200t/d和珠江水泥厂4 000t/d熟料水泥生产线所使用的回转窑均由该公司引进,其托轮均为近代托轮结构。图4d是日本石川岛播磨公司的托轮结构,去掉了辐板,强化了8个支撑筋条。这种托轮结构既不是“死托轮”也不是带辐板的传统托轮,应用在冀东水泥厂φ 4.7m×74m回转窑上,从1982年投产至今已有32年之久,比较可靠。图4e是我国天津水泥工业设计研究院有限公司近年来为设计能力5 000t/d熟料生产线φ4.8m×72m预分解窑所设计的托轮结构,与丹麦史密斯公司的“死托轮”结构基本相同,起吊孔由5个减少到3个。

图4 近代托轮的结构
2 托轮受力的简化
托轮通过轮带支承着回转窑回转部分的全部载荷,轻者几十吨,重者几百吨,视窑的大小而不同。托轮不仅承受着巨大的载荷,而且被轮带带着转动,使托轮辐板承受反复载荷,如图5所示。
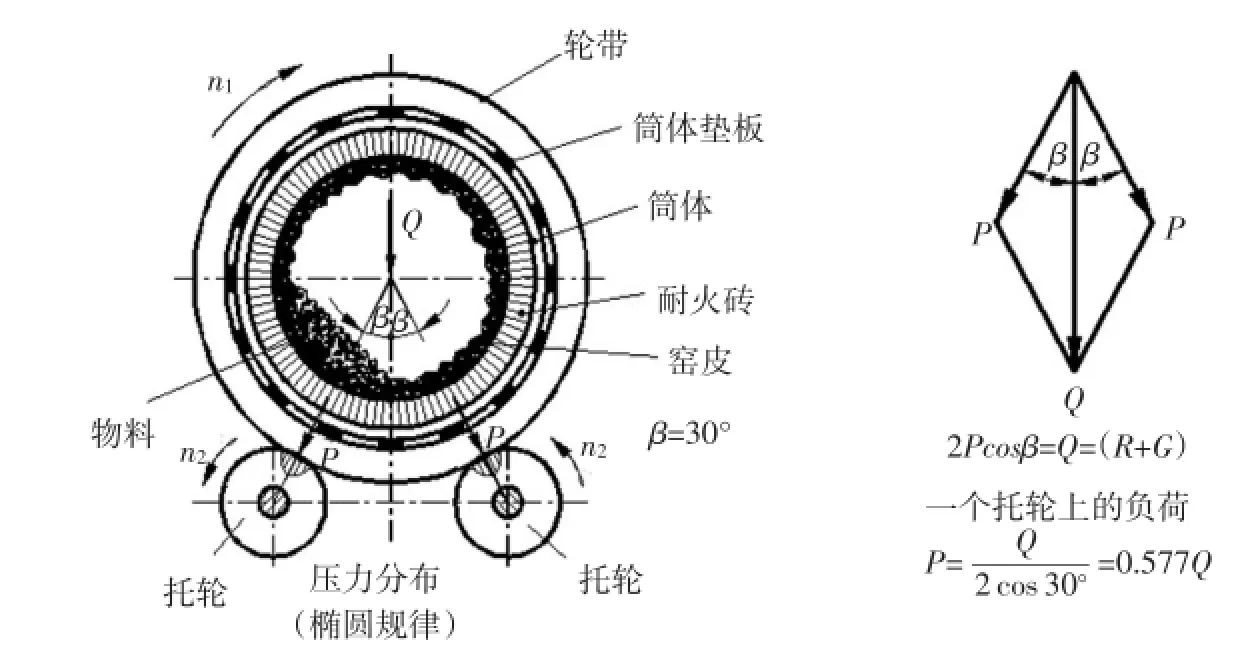
图5 托轮辐板孔的受力分析简图
3 托轮辐板清砂孔的力学分析
托轮的轮缘一般较厚,可认为辐板孔受有均匀的压应力q,孔边不受面力。这样就可以将辐板孔当作弹性力学中的平面问题来分析[1],使其大大简化。
在各种平面问题中,孔口问题最能显示复变函数解法的优越性。有些比较复杂的孔口问题,如不用这种解法,几乎无法求解。在进行保角变换时,最简单是把弹性体在z平面上所占的区域变换成ζη平面上的所谓“中心单位圆”(图6)。据此采用一般复变函数书籍中给出的变换式:均为实数,将复数z=x+iy及ζ=ρeiθ=ρ(cosθ+i sinθ)代入式(1)中,并分开实部与虚部则可得:
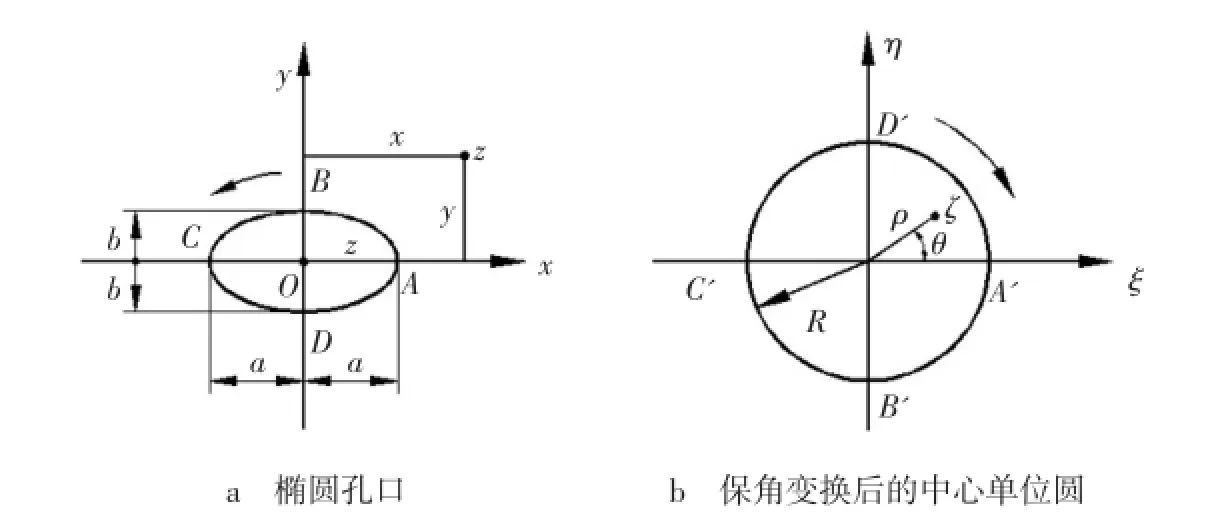
图6 椭圆孔口的分析简图
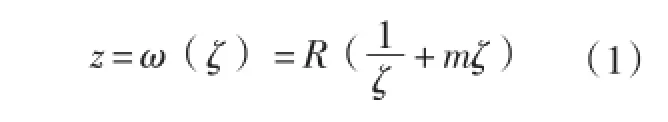
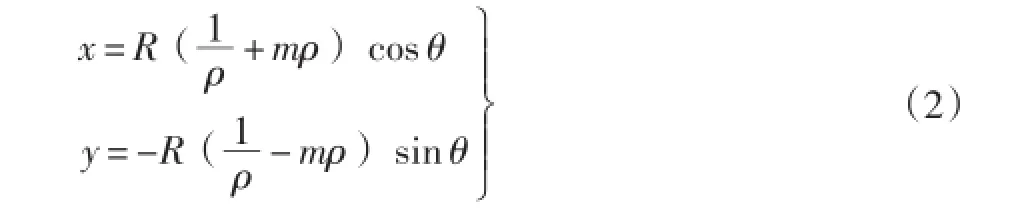
将x和y平方并移相后消去θ得:

再利用x2和y2的关系消去ρ得:
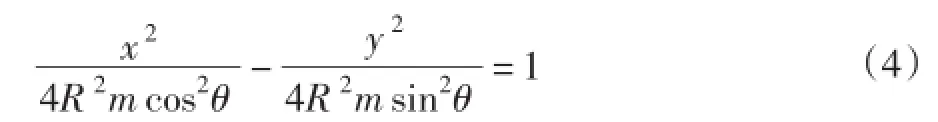
由式(4)可见,在ζ(ζη)平面上ρ=const时的圆周对应于z平面上的椭圆,则有:

当ζ平面上ρ=1时的圆周所对应于z平面上的椭圆则有:

由此可以看出,以a为长半轴和b为短半轴的椭圆即为该椭圆的孔口曲线。
当坐标原点ζ=0时,即ζ平面上中心单位圆的中心是对应于弹性体中距椭圆形孔口曲线无限远的各点。根据式(1)可导出式(7):

可得出函数的公式为:


因为函数
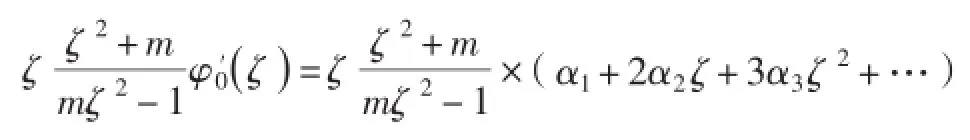
在单位圆之内解析,在圆内和圆周上连续,所以式(10)变为:
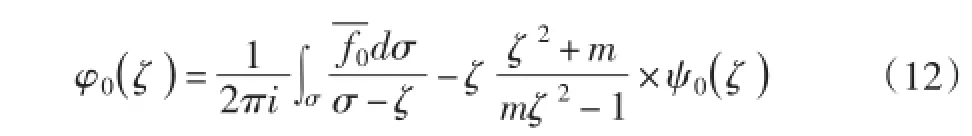
现假设在与x轴成α角的方向受均匀压应力q,孔边不受力(图7),则有:
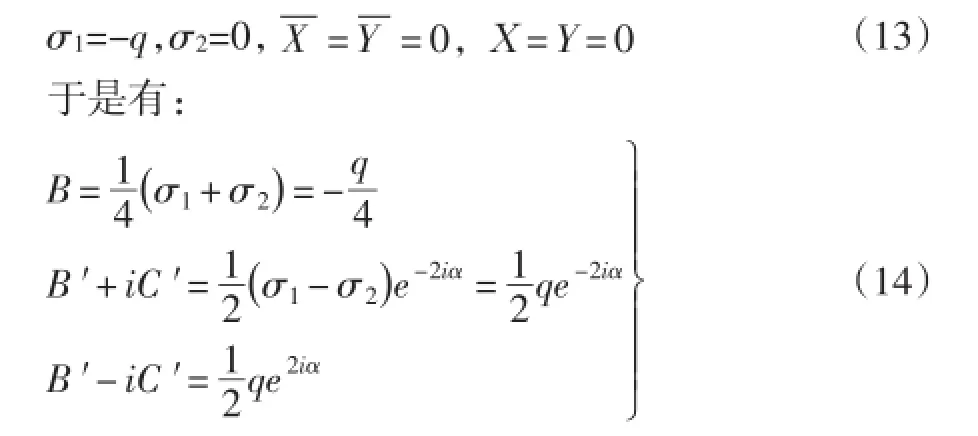
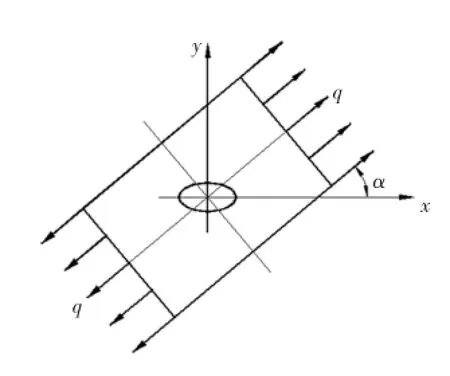
图7 椭圆孔的简化受力状态
这样有:
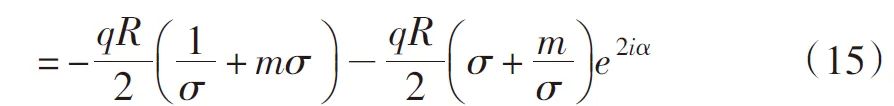
代入式(10)后经运算得:

将式(15)和式(16)代入式(12)后得:
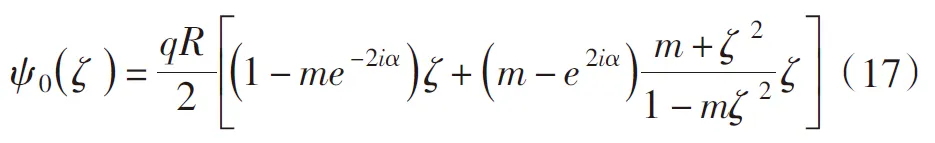
简化得:

接下来求应力分量。

由式(18)求得:

于是有:

从而求得:

中,经简化可得应力分量的复变函数表达式为:

将ζ=ρ(cosθ+i sinθ)代入二式,分开实部与虚部即可得出σρ、σθ和τρθ的表达式[3]。
孔边应力是最重要的应力,绝大部分的辐板孔都是从孔边开始产生裂纹。在孔边,σρ=τρθ=0,ζ=σ,于是由式(23)中的上式得:这就是与水平轴成θ角位置处有关的孔口有关的应力分量表达式。
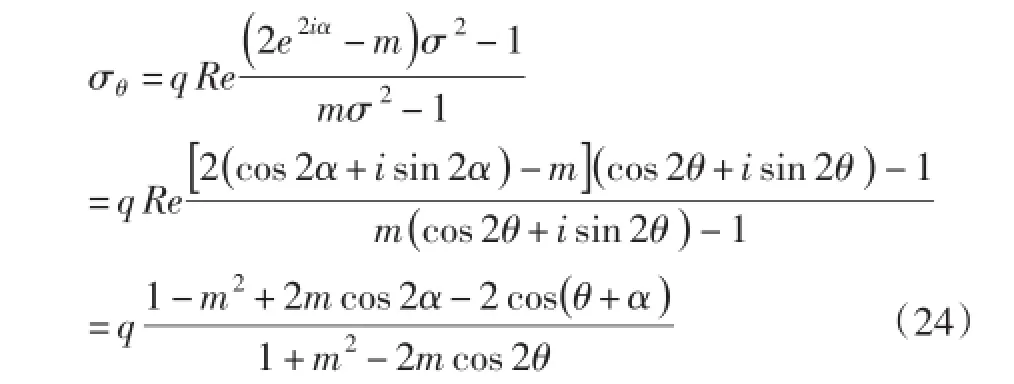
4 讨论
(1)假设椭圆孔的长轴沿托轮的径向设置,即α=0(图7),此时椭圆孔的受力状态如图8所示,可见压力q平行于长轴x。由式(24)得:

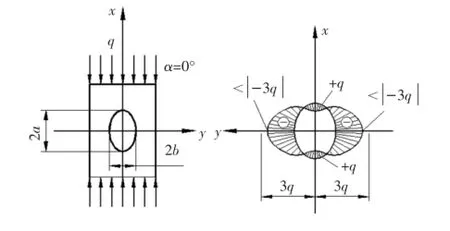
图8 作用力垂直于短轴椭圆孔的应力分布图
在前面推导过程中,q是作为拉力假设的。在此处q是单位压力,所以应变号,即在式(24)前面加一个负号“-”。
为图示方便,将正应力画在圆内,负应力画在圆外。
最大正应力为:
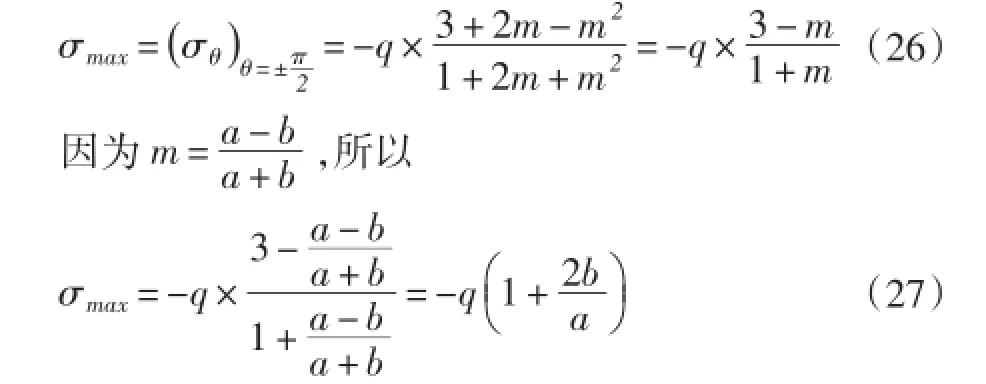
因为a>b,所以σmax<||-3q。当a=b时,即孔为圆孔时,则σmax=||-3q。这就是说,a越大时,σmax越小。最小正应力为:
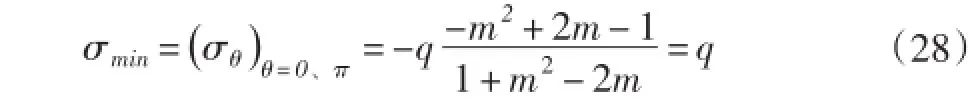
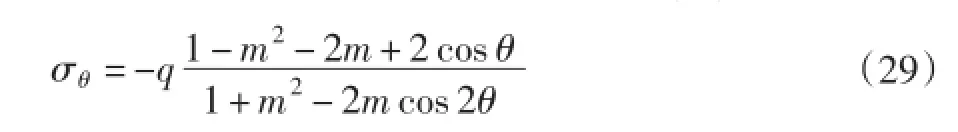
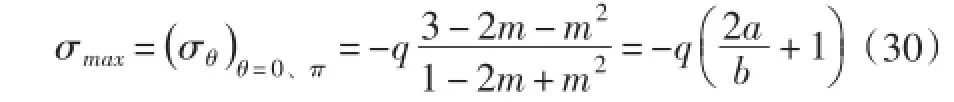
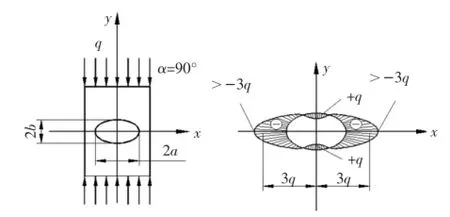
图9 作用力垂直于长轴椭圆孔的应力分布图
最大正应力为:当a=b时,即孔为圆形,σmax=||-3q,与上节结果相同。当a>b时,σmax>||-3q。这就是说,a越大,则σmax的绝对值越大。最小正应力为:

5 结论
通过上述讨论说明:
托轮辐板上采用椭圆孔时,最大正应力的数值与椭圆长短轴的比值有关,与孔的方位无关。不论椭圆孔位置如何设置,最大正应力都发生在长轴的端点。如椭圆孔的长轴为a,短轴为b=,当长轴沿托轮的径向设置时,最大正应力;当短轴沿托轮的径向设置时,最大正应力。这表明同样尺寸和形状的椭圆孔,长轴沿托轮径向设置比短轴沿径向设置的最大应力小得多;如果b=,短轴沿径向设置的最大正应力是长轴沿径向设置的k=倍。
由以上分析可见,采用长轴沿托轮径向设置的椭圆清砂孔是合理的,最大正应力σmax最小。结构允许时,应尽量加大长短轴的比值,使最大正应力σmax更小。采用长轴沿托轮径向设置的椭圆清砂孔,即使托轮磨损严重、轮缘很薄时,也未出现因辐板孔断裂而报废的情况(见图1)。因为是椭圆,a≥b,所以σmax≤||-3q,这说明椭圆孔优于圆形孔。如果采用带辐板的托轮结构时,在设计中应大力推广采用。
圆形孔的最大正应力σmax≡3q,考虑制造的方便,在小型托轮上可以采用。但在大型托轮上应严禁采用,因为它比长轴沿托轮径向布置的椭圆孔其正应力要大。
短轴沿径向设置的椭圆清砂孔是最不好的,它的最大正应力σmax≥||-3q,今后应禁止使用。现在仍在使用此种清砂孔的厂矿,在订备件时应加以改进。实践证明,辐板采用短轴沿径向设置椭圆孔的托轮,发生孔口断裂的问题较为频繁,尤其在大型窑上更为严重,造成很大的经济损失。
6 实例计算
某厂使用德国德骚公司提供的φ4m×60m同规格三条立波尔回转窑,托轮绝大部分因辐板孔断裂而报废(见图2),损失很大。
托轮的结构及主要技术数据见图10和表1。

图10 托轮的主要数据及结构

表1 φ4m×60m立波尔窑托轮力分析的主要参数
筒体的支反力Ri:轮带重量Gt.i:作用在一个托轮上的力:
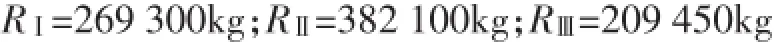

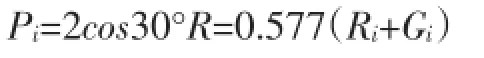
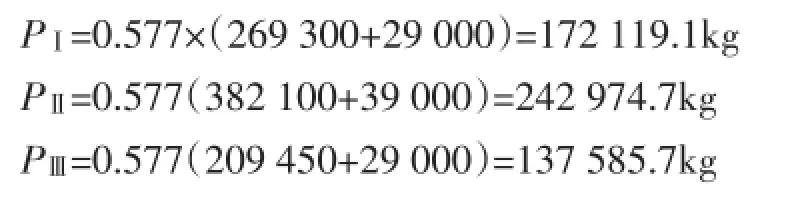
这里有一个比较复杂的问题,就是q值的确定。因为托轮与轮带的接触,是两个不同直径圆柱体的接触,接触面上的压力分布呈椭圆线规律[4],见图2。但是因为一般轮缘都比较厚,可认为传到辐板上的力是均匀的,这样就符合图7所示的情况。
若不考虑纵向筋的影响,取两个相邻纵向筋板之间的弧长为承压长度,则承压长度可按下式计算:
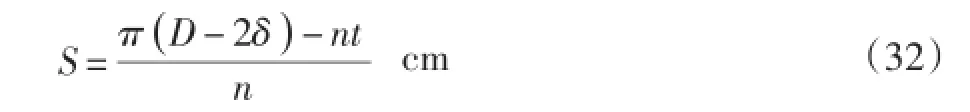

将表1中的有关已知值代入式(32)得:承压面积按式(33)计算:

将表1数值代入式(33)得:

单位承压面积上的作用力q按式(34)计算:

将P、F的相应值代入式(34)中得:

由此可看出:q值相当近似,因为F值的计算与实际出入较大,它既未考虑纵向筋板的影响,也未考虑轮缘在圆周上连续的影响,而是按断开考虑的,然而它有相对的意义。因此,椭圆孔边的理论最大正应力可按式(35)来计算:
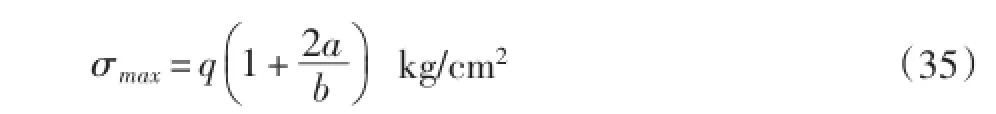
将q、a和b值分别代入式(35)中,可求得椭圆孔短轴沿托轮径向布置孔边最大正应力为:
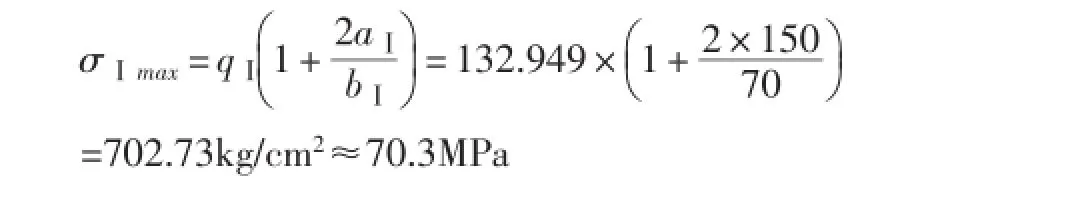

如果同样形状和尺寸的椭圆孔,将长轴转动90°,即长轴沿径向设置时,则孔边应力会减少很多。即当作用外力的方向平行于长轴,将会大大改善椭圆孔的受力状态。此时的最大正应力可按式(36)计算:

椭圆孔短轴沿径向设置时的孔边最大正应力是长轴沿径向设置时的倍数为:

通过上述计算表明,同样的椭圆孔短轴和长轴沿托轮径向设置时,孔边最大的正应力差别悬殊。第Ⅰ档和第Ⅲ档为2.734倍,第Ⅱ档为2.252倍。
由式(35)、(36)可见,椭圆孔边的最大正应力与a、b的绝对值无关,即与孔的大小无关,而与和的比值有关。当长轴沿托轮径向设置时值越大(最大<1),则孔边的最大正应力越大。相反值越小时,则孔边的最大正应力越小。因此,若结构允许,在设计时应尽量增大a值而减小b值。
另外,需要注意的是:孔边的最大正应力总是发生在长轴的两个端点。如果长轴沿托轮径向设置,长轴的两个端点一个靠近轮缘,一个靠近轮毂,由于轮缘和轮毂比较刚固,对孔边有加强作用。而当短轴沿托轮径向设置时,长轴两个端点基本处在轮缘和轮毂的中间,即距轮缘和轮毂最远,得不到它们的加强作用,因此裂纹最易从此发生(见图2),严重时会引起轮缘断裂。
由于在本文的计算中,没有考虑表面粗糙度和孔边圆角应力集中的影响,所以以上求出的最大正应力应称为“理论最大正应力”。
实际上这两种影响是存在且不可忽视的。托轮被轮带带动时,与轮带接触的一瞬间受到最大压力P的作用;当转过接触部位时,此处的压力逐渐减小;若此处转到侧面或下面时则基本不受力。可见,对某个辐板的清砂孔来说,它承受的是一个间断的交变应力,基本上属于脉动正循环载荷。表面粗糙度对其疲劳限有很大影响,如表2所示,表面越粗糙,抗拉强度限越高的材料,即硬度越大的材料,其疲劳强度越低。对铸造表面的疲劳强度没有试验值,但可以估算。

图11 由辐板孔断裂引起轮缘断裂实物照片
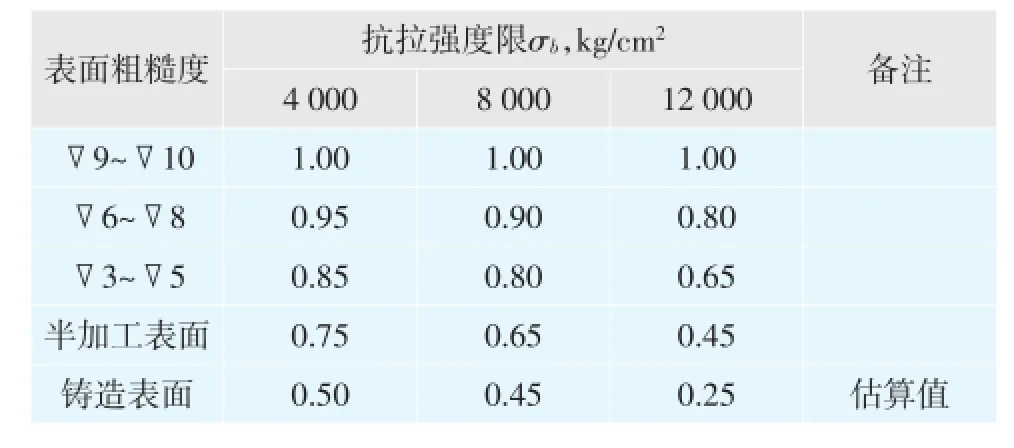
表2 表面粗糙度对疲劳强度的影响系数
孔口边界圆角所产生的应力集中也是不可忽略的,但尚无试验数据可查。在现有托轮的铸造中,辐板孔口边界的圆角往往被忽视,经常铸成直角,极易造成应力集中。更有甚者,连铸造飞边也不处理,使受力极度恶化,更容易在此处产生裂纹。根据国内的铸造水平,在设计时可取应力集中系数αk=1.5~2.0[6]。
国内托轮一般用45~55号钢铸造,多处于回火状态,所以疲劳限可按式(37)确定[6]和表面铸造平整系数βk=0.47。
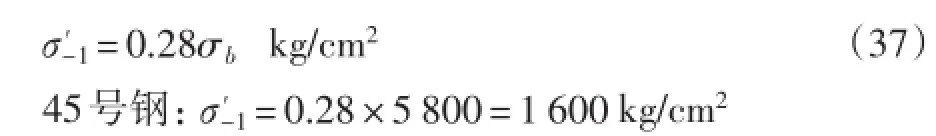
国内托轮原料一般用45~55号钢铸造,多处于四大状态,所以疲劳限可按式(37)确定[6]:50号钢:σ′-1=0.28×6 100=1 700 kg/cm255号钢:σ′-1=0.28×6500=1 800 kg/cm2孔边的实际最大应力可按式(38)计算:

当长轴沿托轮径向设置时,则孔边的实际最大正应力按式(39)计算:
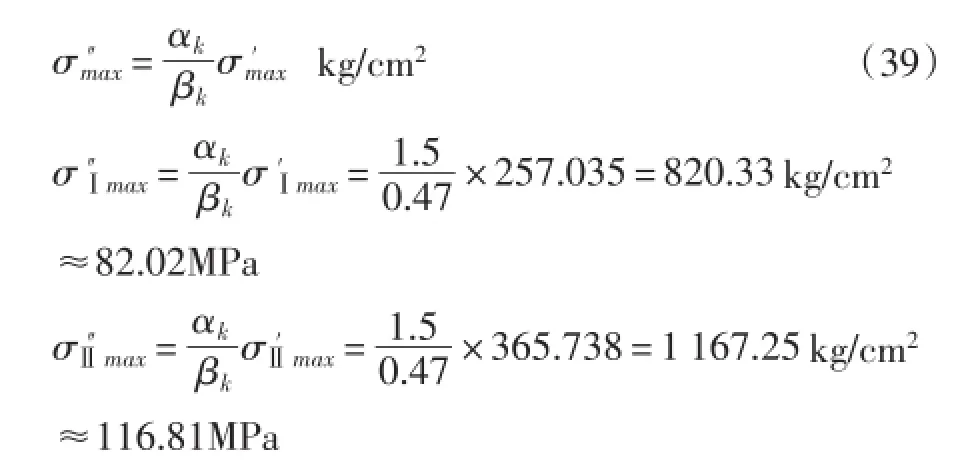
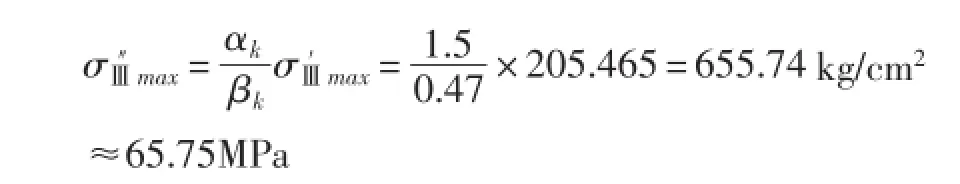
由上述计算可见,当短轴沿托轮径向设置时,实际的最大应力均超过了材料的疲劳限,中档最严重。实际上也是如此,中档托轮坏的最多。当长轴沿托轮径向设置时,实际的最大应力均小于疲劳限。所以,只要将辐板的清砂孔转动90°设计,就会大大减小这种损失。对其他回转窑托轮辐板孔的计算,也都得到同样的结论。
[1]徐芝纶.弹性力学[M].北京:高等教育出版社,1982.
[2]H.ИМусхеличшвцли.数学弹性力学的几个基本问题[M].赵惠元,译.北京:科学出版社,1958.
[3]张芝琪.坝体内孔口和廊道[J].水利水电建设,1959,(14).
[4]武汉建筑材料工业学院,华南工学院,辽宁建筑工业学院.建筑材料机械及设备[M].北京:中国建筑工业出版社,1980.
[5]东北工学院设计教研室.机械零件[M],1956.
[6]Г.С.ПИСАРЕНКО,А.П.ЯКОВЛЁВ,В.В.МАТВЕЕВ.材料力学手册[M],宋俊杰,刘茂江,译.石家庄:河北人民出版社,1982.
TQ172.622.29文献标识码:A
1001-6171(2015)05-0027-08
通讯地址:天津市博纳建材高科技研究所,天津300400;2015-05-18;编辑:孙娟
