拉格朗日中值定理的应用
2015-09-01赵畅
赵 畅
(吉林师范大学 数学学院,吉林 长春 130103)
在数学分析中,微分中值定理主要包括罗尔中值定理、拉格朗日中值定理、柯西中值定理及泰勒公理等.它们是根据导函数的相关性质判断原函数性质的有效工具,还可以借助这些公理和公式求待定式的极限,研究函数的特性,讨论函数作图及求解极限与最值问题等.
微分中值定理中的拉格朗日中值定理更是运用导数这一工具研究函数的依据,也是微分学的许多重要应用的桥梁,在高等数学中应用广泛.
1 拉格朗日中值定理
定理1(罗尔中值定理) 若函数f(x)满足以下条件,
(i)f(x)在闭区间[a,b]上连续;
(ii)f(x)在开区间(a,b)内可导;
(iii)f(a)=f(b),
则在开区间(a,b)内至少存在一点ξ,使得
f'(ξ)=0
定理2(拉格朗日中值定理) 若函数f(x)满足以下条件,
(i)f(x)在闭区间[a,b]上连续;
(ii)f(x)在开区间(a,b)内可导,
则在开区间(a,b)内至少存在一点ξ,使得
2 定理的应用
拉格朗日中值定理作为微分学的重要内容,它的应用十分广泛,下面介绍拉格朗日中值定理在数学分析中的几点应用,对其能够解决的数学问题进行分类和举例说明.
2.1 定理的直接应用
直接应用拉格朗日中值定理的的条件与结论,能解决许多数学问题,并且过程简便清晰.下面分类讨论.
(1)判断根的性质.综合罗尔中值定理、介值定理等定理的内容,可以判断可导函数在给定区间内根的存在性和根的个数.
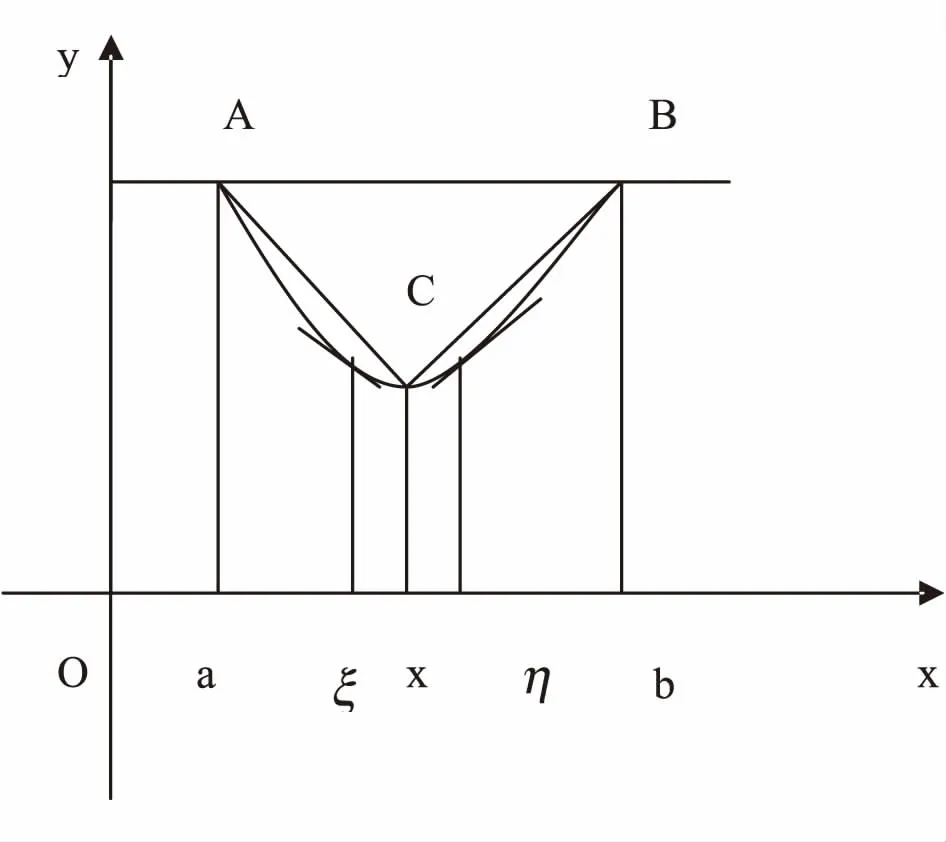
例1 设函数f(x)在闭区间[0,1]上可导,且有0 证明 一方面,证明实根的存在性. 设有函数g(x)=f(x)+x-1,则此函数在闭区间[0,1]上可导.根据已知有g(0)=f(0)-1<0,g(1)=f(1)>0,由介值定理可知,函数g(x)在开区间(0,1)内存在零点,即方程f(x)+x-1=0存在实根. 另一方面,证明实根的唯一性. 利用反证法,假设方程有两个实根x1,x2,且0 综上所述,问题得证. (2)证明等式、不等式.拉格朗日中值定理经过巧妙变形,可以用来证明许多不等式问题. 证明 设函数f(t)=ln(1+t),则函数f(t)在闭区间[0,x]上满足拉格朗日中值定理的条件,故存在点ξ∈(0,x),使得 (3)推导函数的性质.利用拉格朗日中值定理可以推出可导函数的某些整体性质,如单调性,有界性,一致连续性及某些导数极限的性质. 例3 若函数f(x)在开区间(-∞,+∞)内有有界的导函数,则函数f(x)在开区间(-∞,+∞)内一致连续. 证明 根据拉格朗日中值定理,存在∀x1,x2∈(-∞,+∞),有 f(x1)-f(x2)=f'(ξ)(x1-x2),其中 所以函数f(x)在开区间(-∞,+∞)内一致连续. (4)推导其他定理公式.拉格朗日中值定理有一个重要的推广:柯西公式. 例4 设存在函数f(x)、g(x)在闭区间[a,b]上连续,在开区间(a,b)内可导,且导函数g'(x)在开区间(a,b)内处处不为零,则在闭区间[a,b]内存在一点ξ,使得 证明 当函数g(x)=x时,与拉格朗日中值定理内容相同,利用拉格朗日中值定理的证明方法即可. 当函数g(x)≠x时,作辅助函数φ(x)=f(x)[g(b)-g(a)]-g(x)[f(b)-f(a)],由已知可得φ(a)=φ(b).因此函数φ(x)在闭区间[a,b]上为常数或者在此区间内取得最大值、最小值.根据拉格朗日中值定理,存在一点ξ(a<ξ 拉格朗日中值定理的几何意义有较为广泛的应用. 例5 设f(x)是可导函数,导函数f'(x)严格单调递增,若f(a)=f(b)(a 证明 如图1所示,在图中作弦AC,BC,任取一点x∈(a,b),故存在ξ∈(a,x),η∈(x,b),使其导数f'(ξ),f'(η)分别等于弦AC,BC的斜率,且由于导函数f'(x)严格递增,所以f'(ξ) 又由于f(a)=f(b),代入上述不等式,有 f(x) 图1 拉格朗日中值定理几何意义的应用图 借助拉格朗日中值定理的证明思路构造不同的辅助公式,再由有限增量公式 f(b)-f(a)=f'(ξ)(b-a),ξ∈(a,b) 可以导出新的中值公式.下面举例说明. 例6 设函数f(x)在闭区间[a,b]上连续,在开区间(a,b)内存在二阶导数,证明存在一个点c∈(a,b),使 (1) 证明 式(1)左端 拉格朗日中值定理的变形公式指出了函数与导数的一种关系,特别地,这个公式相当于f(x)的泰勒公式展开式中至0次项,因此,可以利用这种关系研究函数的性质. 例7 函数f(x)在区间[0,+∞)上可导,且f(0)=0,设有实数A>0,使得|f'(x)|≤A|f(x)|在x∈[0,+∞)上成立,证明对∀x∈[0,+∞)有f(x)≡0. 证明 由已知可得,函数f(x)在区间[0,+∞)上可导,且f(0)=0,根据拉格朗日中值定理,有 |f(x)|=|f(0)+f'(ξ1)(x-0)|= 拉格朗日中值定理是高等数学中重要的基础定理之一.不仅定理本身具有很高的研究价值,它的应用也十分广泛.本文重点介绍了运用拉格朗日中值定理研究函数的性质、求解极限及最值问题等.这可为学生学习高等数学提供便利,其实拉格朗日中值定理的研究空间还很大,有待学者去继续探索.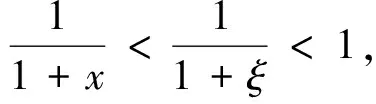
ξ∈(x1,x2).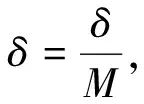
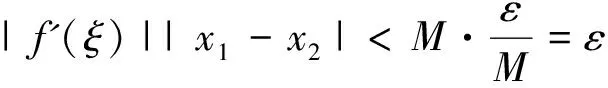
2.2 定理几何意义的应用
2.3 有限增量公式的应用
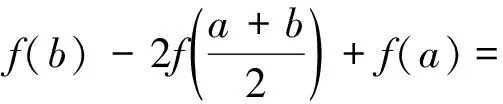
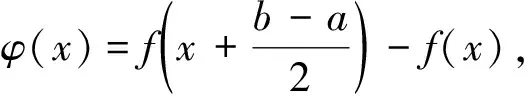
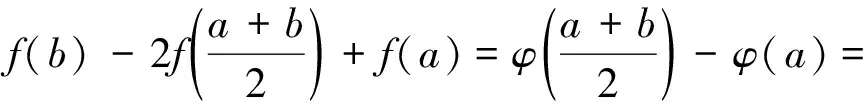
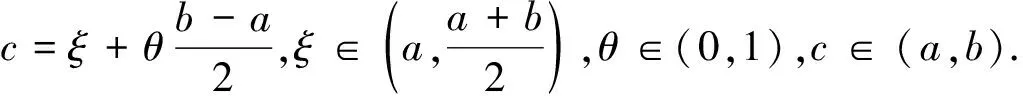
2.4 函数变形的应用
|f'(ξ1)x|≤A|f(ξ1)|x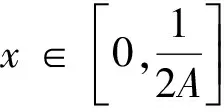
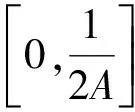
3 小结
