基于响应面的渔船球鼻艏参数分析及多航速自动优化
2015-09-01刘成岗1毛筱菲2吴铭浩2煜21中国舰船研究设计中心湖北武汉4300642武汉理工大学交通学院湖北武汉430063
刘成岗1,毛筱菲2,吴铭浩2,陈 煜21中国舰船研究设计中心,湖北武汉4300642武汉理工大学交通学院,湖北武汉430063
基于响应面的渔船球鼻艏参数分析及多航速自动优化
刘成岗1,毛筱菲2,吴铭浩2,陈煜2
1中国舰船研究设计中心,湖北武汉430064
2武汉理工大学交通学院,湖北武汉430063
远洋金枪鱼围网渔船是一种中、高速的作业型船舶,加装球鼻艏并进行优化可以有效降低其兴波阻力。通过一种改造型值的球鼻艏变换方法,由球鼻艏的长度、宽度、高度及尖点高度参数直接生成用于CFD计算的船体型值,可以快速探讨球鼻艏对兴波阻力的影响。兴波阻力的计算采用Rankine源势流理论,运用试验设计方法生成球鼻艏参数对兴波阻力影响的响应面模型。该模型表明,各参数的影响是复杂且耦合的,难以呈现单调的规律性,且在不同航速下其影响规律也有差异。优化球鼻艏的过程选用结合响应面的快速优化方法,通过优化,发现传统的对单一设计航速的优化可能会出现在较低的服务航速下阻力增加的情形,而采用多个航速的阻力优化方法则在设计航速与服务航速下同时具有减阻节能效果。
围网渔船;球鼻艏参数分析;兴波阻力;响应面;多航速球鼻艏优化
0 引言
金枪鱼围网渔船是一种性能要求较高的渔船,因作业时需要以超越鱼群的速度全速行进并与辅助小艇共同完成围网任务,故其航速通常可达14~18 kn[1]。在设计航速下,傅汝德数Fr>0.3;在服务航速下,Fr>0.25,其中兴波阻力占据了可观的成分,而设计合适的球鼻艏可以有效减少兴波阻力,利于高航速完成作业任务。作为一种特殊的艏部形式,球鼻艏的形状千变万化,若采用手工方法进行方案设计和比选,难以抓住其主要规律,费时费力;而采用先进的自动优化方法进行设计则可大幅减少设计中的人工工作量,使设计过程高效、可靠。
随着船舶CFD与计算机技术的发展,多学科优化设计方法已被广泛运用于船舶的整体与局部自动优化设计中[2-5]。以兴波阻力为目标的球鼻艏优化,是典型的基于CFD的船体局部优化问题。与全船整体自动优化类似,要实现球鼻艏的自动优化需解决4大关键技术问题,即球艏几何外形的参数化表达和重构技术、CFD数值分析技术、近似技术及最优化技术[4-5]。对本文所研究的围网渔船球鼻艏优化而言,几何参数化重构技术即为球鼻艏的生成、变换与参数化控制,其中自动生成的几何模型应与性能计算软件自动相连,以实现自动的精细数值计算;CFD数值分析技术则依赖可靠的理论方法,以完成具有球鼻艏船型的兴波阻力计算;响应面近似技术的运用不仅可以提炼出受球鼻艏参数影响的数学模型,还可加速优化效率,减少优化时间。传统的球鼻艏优化主要是针对设计航速,在其他航速段并不能保证可以减小阻力。随着EEDI指标的推行,运输型船舶通过降低服务航速来降低能效指标、优化球鼻艏实现节能要求已经成为一种流行的做法。对于渔船这种作业与运输特点兼备的船舶,本文拟提出针对多个航速的多目标最优化技术,可在设计航速和服务航速时均能达到减阻节能的效果,以满足围网渔船全速作业围网的任务要求和在服务航速下航行时节能的要求。
1 球鼻艏几何重构技术
1.1球鼻艏型线设计简述
球鼻艏的型线设计是完成球鼻艏优化的基本工作。由于球鼻艏的形状复杂,控制参数多,一些学者便使用参数化设计方法[6-7]利用样条曲面生成球鼻艏,这可在不具备球鼻艏的船前直接生成球鼻艏并保证其与主船体光顺连接,自由改变球鼻艏的形状特征,但控制参数较多,曲面生成步骤复杂,不易进行优化。另一种常见的办法是在已有球鼻艏的基础上进行改造,如叠加贝塞尔曲面法[8]、形状融合法[9]。参数化船舶建模软件Friendship-Framework提供的三角变换功能也可完成对球鼻艏形状的局部重构,其与阻力详细计算软件SH IPFLOW的无缝连接使其被广泛应用于球鼻艏的设计与优化中。更为简便的方法是直接对型值进行改造[10-11]。本文所研究的金枪鱼围网渔船本身具备球鼻艏,采用基于球鼻艏形状控制参数的型值改造变换方法可以快速完成球鼻艏变换,更加适用于自动优化设计过程。
1.2球鼻艏自动变换方法
球鼻艏虽然形状复杂,但通常可以采用无因次化的横剖面积参数、侧面积参数、体积参数、宽度参数、长度参数以及高度参数等特征参数来表达[12]。
本文选用无因次化的长度参数FL、横剖面高度参数FZ、宽度参数FB,以及尖点高度参数FH这4个参数(图1)。


图1 球鼻艏形状特征参数Fig.1 Characteristic parametersofbulb bow
采用简单的型值变换原理对母型船球鼻艏进行改造,步骤如下:
1)确定变换坐标系,以球鼻艏首垂线与基线的交点为变换坐标系的原点,X,Y,Z方向分别为长、宽、高3个方向。
2)在X,Y,Z这3个方向分别使用长度拉伸系数CX、宽度拉伸系数CY和高度拉伸系数CZ对球鼻艏部分型值进行仿射变换。
3)考虑到与船体的衔接,将球鼻艏切除线(为具备球鼻艏剖面在球鼻艏上方的第1个拐点)的垂向坐标采用二次抛物线变换,对切除线以上部分型值进行垂向平移,对切除线以下部分则采用对每一站对应的横向与纵向仿射系数进行仿射变换。
4)球鼻艏尖点相对高度参数CH反映了尖点的位移,位移后的球鼻艏纵剖线采用二次抛物线变换,对每一站型值进行对应的垂向平移。在步骤3)与步骤4)中,采用的抛物线变换法是指利用简单的D Z(X)=AX2+B型式抛物线,在需要变换的区间两端予以满足,求出系数A与B,继而得到每一个球鼻艏剖面的垂向位移量。
图2为球鼻艏变换的几何示意图。根据以上原理,通过编写球鼻艏变换程序,完成球鼻艏的几何重构,自动生成符合相关CFD软件型值格式的船体与球鼻艏型值文件,可直接用于数值计算。

图2 球鼻艏变换Fig.2 Transformation of bulb bow
2 基于响应面的球鼻艏参数、兴波阻力影响分析
2.1兴波阻力数值计算
对于船舶兴波阻力求解,势流理论方法快速而有效[13]。本文兴波阻力采用Shipflow软件中基于三维Rankine源的势流方法计算。母型船的主要尺度如表1所示。

表1 金枪鱼围网渔船主要尺度Tab.1 Principaldim ensionsof a purse seiner
船体网格划分为船体(Hull)、球鼻艏(Bulb)、球艉(Boss)和船艉平台(Overhang)4个区域。自由面划分为前方自由面、中部自由面与尾部自由面,船艉区域取1.5倍船长。网格划分方式如表2和图3~图4所示,计算模型如图5所示。

表2 船体网格划分Tab.2 Hu llm esh

图3 自由面网格划分Fig.3 Panelmesh on free surface

图4 球鼻艏网格划分Fig.4 Panelmesh on bulb bow

图5 计算模型Fig.5 Calculationmodel
2.2响应面模型的建立
球鼻艏形状对兴波阻力的影响主要反映在球鼻艏的控制参数上,了解这些控制参数所起的作用,分析其影响的重要程度是设计球鼻艏的关键。在本文的研究中,为全面而高效地探索4个球鼻艏设计参数所构成的设计空间,采取了一种基于响应面的分析方法[14]。响应面的数据来源于均布于全空间的超拉丁方法试验设计方法(Latin Hypercubes DOE),设计变量的选取范围均为±15%,如表3所示。

表3 试验设计变量范围Tab.3 Range of variables in Design of Experiment(DOE)
响应面模型的建立采用四次多项式,令

式中,下标0表示与母型船相关的参数。由X1~X4构成的响应面的23个分项系数如表4所示。输出指标为详细兴波阻力计算所得到的兴波阻力系数CW,该响应面模型精度的相关系数为R2=0.989。通过建立响应面,便可清晰、直观地看出各参数的影响程度。

表4 球鼻艏参数对兴波阻力影响的响应面Tab.4 Coefficients of the response sur face of bu lb bow param eters'influences on wavem aking resistance
2.3球鼻艏参数对兴波阻力影响分析
2.3.1球鼻艏纵剖面形状的影响
球鼻艏的纵剖面形状由FL和FH这2个参数控制,其与兴波阻力构成的响应面在不同的横剖面形状控制参数下呈现出一定的不规律性。如图6和图7所示,当FB=0.225,FZ=0.680时,球鼻艏的长度系数增加,艏尖点略微下沉,此时可以降低设计航速时的兴波阻力系数。然而当FB=0.258,FZ=0.782时,响应面呈现马鞍形和多个阻力较小的区域,尖点下沉将不能减小兴波阻力,这说明这2个参数的影响规律并不单一,需要有较好的配比才具减阻效果。

图6 CW-FL-FH响应面(FB=0.225,FZ=0.680,Fr=0.326)Fig.6 CW-FL-FHresponse surface(FB=0.225,FZ=0.680,Fr=0.326)

图7 CW-FL-FH响应面(FB=0.258,FZ=0.782,Fr=0.326)Fig.7 CW-FL-FHresponse surface(FB=0.258,FZ=0.782,Fr=0.326)
球鼻艏的横剖面形状由宽度系数FB与高度系数FZ控制。通过响应面(图8、图9)可以观察到,相比于纵向控制参数,这2个系数对兴波阻力的影响更为敏感,且受纵剖面形状影响较小。对于本航速(Fr=0.326),FB在0.24附近时为最佳,而球鼻艏高度系数较大时比较有利。
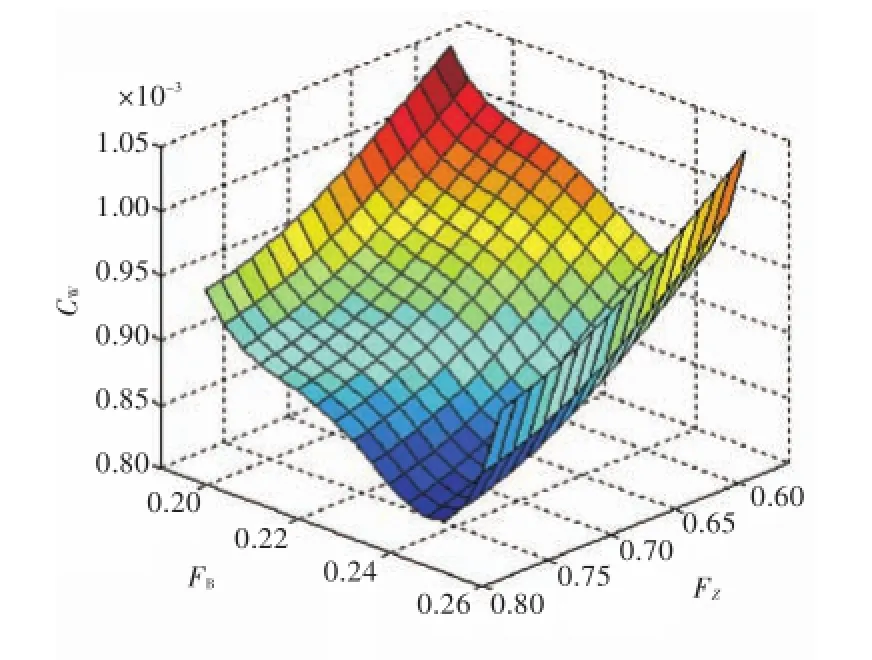
图8 CW-FB-FZ响应面(FL=0.058 7,FH=0.621,Fr=0.326)Fig.8 CW-FB-FZresponse surface(FL=0.058 7,FH=0.621,Fr=0.326)
2.3.2球鼻艏横剖面形状的影响

图9 CW-FB-FZ响应面(FL=0.0675,FH=0.621,Fr=0.326)Fig.9CW-FB-FZresponsesurface(FL=0.0675,FH=0.621,Fr=0.326)
2.3.3不同航速下球鼻艏参数的影响
图10与图11所呈现的响应面分别为Fr=0.244、服务航速为12kn时球鼻艏纵剖面形状参数与横剖面形状参数对兴波阻力的影响。通过对比图10与图6可观察到,长度参数FL的影响趋势在设计航速和服务航速这2个航速下相近,但FH的影响趋势与Fr=0.326时相反,该值越小越有利。同时通过对比图11与图8可知,响应面的“脊线”在不同航速时发生了较明显的变化。横剖面的2个参数均未对兴波阻力产生单调的影响。

图1 0CW-FL-FH响应面(FB=0.225,FZ=0.680,Fr=0.244)Fig.10CW-FL-FHresponsesurface(FB=0.225,FZ=0.680,Fr=0.244)

图1 1CW-FB-FZ响应面(FL=0.0587,FH=0.621,Fr=0.244)Fig.11CW-FB-FZresponsesurface(FL=0.0587,FH=0.621,Fr=0.244)
通过以上分析可知,球鼻艏控制参数相互耦合对兴波阻力系数的影响极其复杂,在不同航速下,由于产生了不同的消波效应,参数的影响呈现出非单调性,难以通过一般的规律进行设计,需采用单目标或多目标优化的手段找到最适合的参数搭配。
3 基于响应面的球鼻艏优化
3.1设计航速下的球鼻艏优化
通过试验设计方法形成的响应面不仅可以观察到各变量对兴波阻力的影响,也可作为目标函数运用到优化过程中。在相应的响应面近似模型上进行优化计算不仅能大大减少直接调用CFD软件进行计算的时间,也能平滑设计空间的数值噪声,防止数值优化方法陷入局部极值点[5,14]。
3.1.1优化数学模型及过程
球鼻艏优化目标函数的数学模型如下:

对应的航速为设计航速16kn,Fr=0.326。各设计变量范围与试验设计的变量范围保持一致,可参见表3。
为满足船舶浮态要求,排水量和湿面积的变化应不超过0.5%,约束条件如表5所示。

表5 约束条件Tab.5Constraints
优化采用组合优化策略进行,其中全局寻优采用多岛遗传算法MIGA,局部寻优采用广义既约梯度方法GRG法[5,14]。共经历了3514次迭代,得到最优解船型,命名为优化船I。迭代历程如图12所示。优化船I的球鼻艏参数、湿表面积与排水量如表6所示。

图12 全局寻优历程Fig.12Globalsearch
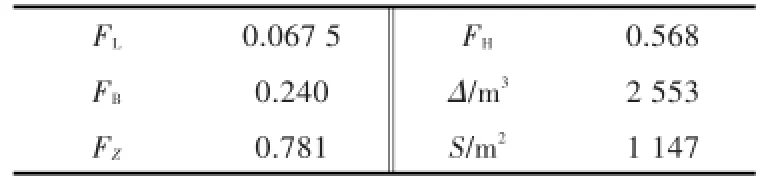
表6 优化船I球鼻艏参数Tab.6Bulbbowparametersofoptimal-I
3.1.2优化结果分析
图13与图14展示了球鼻艏优化后,设计航速下的兴波波形图与波切面图。从中可明显看到,优化球鼻艏有效降低了船艏肩处的第1个波系,这得益于球鼻艏产生的有利波系干扰,而对船艉的波系影响不大。

图13 波形图Fig.13Wavepattern

图14 波切面图(Y=0.2LPP)Fig.14Wavecutprofile(Y=0.2LPP)
表7和图15显示了母型船与优化船I在12~17kn航速下的兴波阻力系数及曲线。从中可以看出,针对设计航速的兴波阻力优化,在Fr>0.29及以上的航速段取得了较好的效果,兴波阻力在15,16,17kn时分别减小了10.03%,17.35%和17.38%;而在Fr<0.28的航速段(12~14kn),兴波阻力有一定的增大,说明单个设计航速点的球鼻艏优化在设计航速附近可降低阻力,但在较低服务航速附近航行时阻力反而有所增加,从而有可能增加航行阶段的能耗。为既能满足本船围网捕鱼时冲击高速的需求,又能满足航行时的节能降耗,需要采用多航速点优化来加以实现。
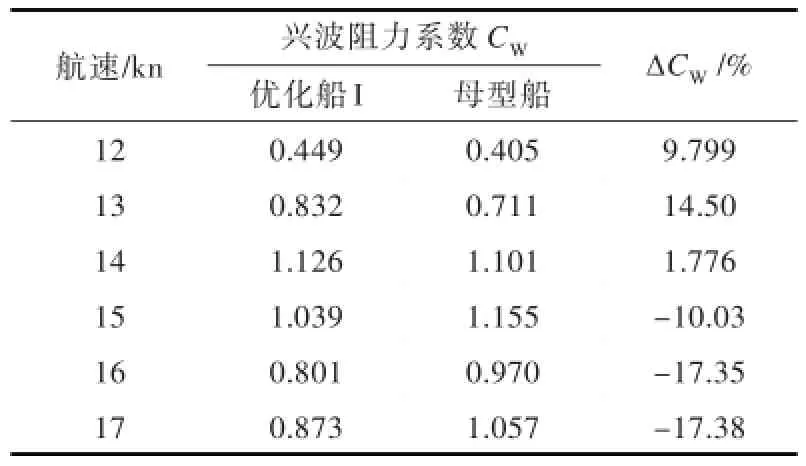
表7 优化船I与母型船兴波阻力系数比较Tab.7 Comparison of wave resistance coefficients between original andoptimal-Iships

图15 优化船I与母型船兴波阻力系数曲线比较Fig.15Comparisonofwaveresistancecoefficientcurves betweenoriginalandoptimal-Iships
3.2多航速下的球鼻艏优化
与单航速阻力优化类似,多航速下的优化目标函数数学模型如式(4):

相关约束条件同表3和表5。
本文中选取Fr1=0.25,Fr2=0.326,分别对应于服务航速和设计航速。优化采用支持多目标优化的非支配遗传算法NSGA-II。非支配遗传算法更加适用于该类多目标优化问题,而改进的非支配遗传算法NSGA-II则采用了更快速的精英算法,可大幅提高运算效率[15]。经过5000余次迭代,得到如图16所示的Pareto前沿解集,通过人工决策方式,选择了两个航速下兴波阻力系数均较低的前沿解,命名为优化船II,其球鼻艏参数如表8所示。图16同时还标注出了母型船、优化船I这2个解在解空间中的位置,可以注意到,优化船I的解靠近了Pareto解集的最边缘,说明船体在不同航速下的阻力系数可能是矛盾的关系,在进行阻力优化时,需要从全航速的角度出发,既要保证船舶的最高航速,又要满足节能航行的需求。

图16 多航速兴波阻力优化Pareto前沿解集Fig.16 Pareto solutionsofmulti-speed wave resistance optimization

表8 优化船II球鼻艏参数Tab.8 Bulb bow param etersof op tim al-II
表9为优化船II与母型船的计算兴波阻力系数对比。图17为母型船、优化船I与优化船II这3个方案的兴波阻力系数曲线比较。从中可以看到,优化船II在服务航速时的兴波阻力系数计算值和母型船相比减小了6.3%,在设计航速时减小了9.36%,在航速13~15 kn之间,优化船II的兴波阻力系数与母型船相比并未增加,说明这一方案在全速航行作业和服务航速航行时都具有较好的节能效果。
图18为3种球鼻艏的比较图。从纵剖面来看,2个优化后的球鼻艏均伸长了,这改善了干扰波系形成的位置,同时,优化船I的上翘较明显,增强了波系的强度,符合高航速下用“SV球鼻艏”的理念。从横剖面看,2个优化船的球鼻艏高度均增加了,这是因为高度增加,球鼻艏离水面更近,产生的有利干扰便更强烈。而优化船II的球艏高度看起来要比优化船I小一些,反映了一种满足不同航速要求下的“折中”选择。
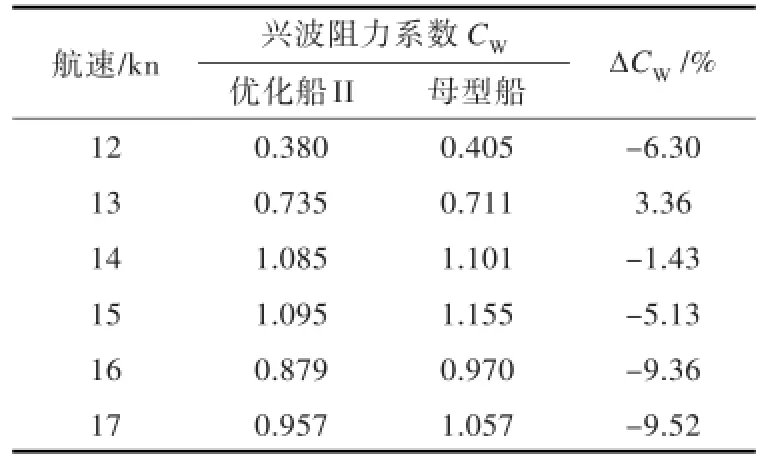
表9 优化船II与母型船兴波阻力系数比较Tab.9 Com parison ofwave resistance coefficients between original and optim al-IIships

图17 优化船与母型船兴波阻力系数曲线比较Fig.17 Comparison ofwave resistance coefficient curvesbetween original and optimalships

图18 三种船型的球鼻艏剖面对比图Fig.18 Comparisons ofbulb bow profilesof the three ships
4 模型试验
金枪鱼围网渔船母型船与优化船I的阻力试验在武汉理工大学的船模拖曳水池进行。船模为光体,试验得到的阻力按三因次法换算为总阻力。图19为修改后的优化船I的船体模型。

图19 优化船I船体模型Fig.19 Shipmodelofoptimal-I
理论求解得到的总阻力按下式计算:

式中:CF由相当平板公式得到;k由Holtrop公式得到[16];CW为由势流计算得到的兴波阻力。
图20为母型船与优化船I的模型试验值及理论计算值比较。可以看出,计算的结果趋势与试验是吻合的。试验中,优化船I在设计航速为16 kn时总阻力有5.09%的减阻效果,同时也验证了本船计算中对设计航速优化可能导致服务航速中阻力增加的情况。不过,在较低航速时阻力计算值与试验值有一定的误差,其原因可能有2点:一是粘性阻力经验公式的值与实际船模试验值间的误差;二是为维持不同航速下兴波阻力计算和自动优化的稳定性,本文对兴波阻力的计算网格更偏重于计算的收敛性,造成了少许精度损失。

图20 船模试验与数值计算阻力曲线对比Fig.20 Comparison of resistance curvesbetween model testand numericalanalysis
5 结论
本文采用了一种直接基于球鼻艏特征参数的球鼻艏型值变换方法,探索了金枪鱼围网渔船4个控制参数与船体兴波阻力间的联系,完成了一系列优化计算,得到以下主要结论:
1)结合试验设计方法与响应面方法,生成了不同航速下各球鼻艏参数对兴波阻力影响的响应面。响应面揭示了球鼻艏各参数之间复杂的耦合影响:球鼻艏横剖面内的控制参数对兴波阻力的影响程度要强于纵剖面内的,除球鼻艏增长会降低兴波阻力外,其他各参数均没有特定的规律。
2)将基于响应面的优化设计方法运用于球鼻艏的设计,采取组合优化的策略,可以快速、有效地得到优化解。
3)不同航速下,球鼻艏参数的影响规律不统一。这说明对设计航速来说较好的球鼻艏在其他航速下并不一定能达到节能效果。仅针对设计航速的优化结果(优化船I)在16 kn设计航速下时减小兴波阻力17.35%,但在其他航速段兴波阻力出现了增加。模型试验也反映了这一问题。而针对多航速的兴波阻力优化(优化船II)则可以控制服务航速和设计航速之间各速度点的阻力性能,有助于经济航速下的节能降耗。
4)在Vs=16 kn,Fr=0.326时,优化船I呈现上翘的SV型,球鼻艏的宽度和高度均增加。而优化船II的设计点更偏重于服务航速,球鼻艏横剖面显得瘦削,球鼻艏略为下沉。
此外,在船舶阻力的优化中,以往常采用针对设计航速进行优化的做法来满足速度指标的需求,然而随着EEDI指标的执行,船舶降低服务航速的方法已经被广泛采用,单一的针对设计航速的优化已不能满足节能降耗的要求。本文所实现的多航速优化,也为EEDI指标下的船体型线阻力优化提供了思路。
1]周崇庆,贾复,陈龙.金枪鱼围网渔船的快速性分析[J].中国水产科学,1998,5(4):77-81. ZHOU Chongqing,JIA Fu,CHEN Long.Analysis of resistance and propulsion for tuna seiner[J].Journal of Fishery Science of China,1998,5(4):77-81.
[2]KIM H,YANG C,KIM H J,et al.A combined local and global hull form modification approach for hydrodynamic optimization[C]//28th Symposium on Naval Hydrodynamics.Pasadena,California,2010:1219-1231.
[3]PERID,CAMPANA E F.Multi-disciplinary optimization of a fishing vessel in variable loading conditions [C]//Annual Conference of Thematic Network MARNET-CFD.Crete,2001.
[4]赵峰,李胜忠,杨磊,等.基于CFD的船型优化设计研究进展综述[J].船舶力学,2010,14(7):812-821. ZHAO Feng,LI Shengzhong,YANG Lei,et al.An overview on the design optimization of ship hull based on CFD techniques[J].Journal of Ship Mechanics,2010,14(7):812-821.
[5]钱建魁.基于水动力性能的船型多学科优化设计[D].武汉:武汉理工大学,2011.
[6]徐俊路.球首参数化设计方法及程序实现[D].武汉:武汉理工大学,2009.
[7]PÉREZ F,SUÁREZ J A,CLEMENTE J A,et al. Geometric modelling of bulbous bows with the use of non-uniform rational B-spline surfaces[J].Journal of Marine Science and Technology,2007,12(2):83-94.
[8]李胜忠,赵峰.基于Bezier Patch几何重构技术的船舶球艏构型优化设计研究[C]//第二十三届全国水动力学研讨会暨第十届全国水动力学学术会议文集.西安,2011:496-502.
[9]冯佰威,刘祖源,詹成胜,等.基于CFD的集装箱船球首阻力优化研究[C]//2010年MIS/S&A学术交流会议论文集:中国造船工程学会学术论文集.上海,[2010:249-254.
[10]张宝吉,马坤,纪卓尚.基于势流理论的集装箱船型球首优化设计研究[J].武汉理工大学学报(交通科学与工程版),2011,35(3):505-508. ZHANG Baoji,MA Kun,JIZhuoshang.Study on optimal design of bulbous bow for a container vessel based on potential flow theory[J].Journal of Wuhan University of Technology(Transportation Science& Engineering),2011,35(3):505-508.
[11]林焰,纪卓尚,李铁骊,等.减阻球首优化设计方法[J].大连理工大学学报,1999,39(6):785-791. LIN Yan,JIZhuoshang,LITieli,etal.Optimumapproach to bulbous bow design to reduce resistance and improve propulsion[J].Journal of Dalian University of Technology,1999,39(6):785-791.
[12]顾敏童.船舶设计原理[M].2版.上海:上海交通大学出版社,2001.
[13]徐力,陈作钢.船体艏部水动力性能优化[J].中国舰船研究,2012,7(2):37-41,64. XU Li,CHEN Zuogang.Hydrodynamic performance optimization of ship hull's forebody[J].Chinese Journal of Ship Research,2012,7(2):37-41,64.
[14]钱建魁,毛筱菲,王孝义,等.基于CFD和响应面方法的最小阻力船型自动优化[J].船舶力学,2012,16(1):36-43. QIAN Jiankui,MAO Xiaofei,WANG Xiaoyi,et al. Ship hull automated optimization of minimum resistance via CFD and RSM technique[J].Journal of Ship Mechanics,2012,16(1):36-43.
[15]DEB K,PRATAP A,AGARWAL S,et al.A fast and elitist multiobjective genetic algorithm:NSGA-II [J].IEEE Transactions on Evolutionary Computation,2002,6(2):182-197.
[16]HOLTROP J,MENNEN G G J.An approximate power prediction method[J].International Shipbuilding Progress,1982,29:166-170.
[责任编辑:卢圣芳]
Parameter investigation and multi-speed automatic optimization of fishing vessel's bulb bow based on the response surface
LIU Chenggang1,MAO Xiaofei2,WU Minghao2,CHEN Yu2
1 China Ship Developmentand Design Center,Wuhan 430064,China
2 Schoolof Transportation,Wuhan University of Technology,Wuhan 430063,China
The pelagic tuna purse seiner is amedium-high speed fishery vessel.To reduce its wave resistance,an optimized bulbous bow is usually installed.In order to effectively investigate the bulb bow effect on the wave resistance,a bulb bow transformation method is developed in this paper,through which the bulb bow offsets are transformed into length,breadth,height,and fore-point height parameters and directly used in CFD calculation.The wave resistance is then solved with the Rankine source panel method.Using the method of experimental design,a response surface model of bulb bow parameter effect on wave resistance is generated.The response surface model indicates that the influences are rather complex,coupled and irregular,and the exact rules differ with speed.Finally,a fast optimization method based on the response surface is applied into the bulb bow optimization,and it is noticed that the optimal solution for the design speed could yield worse resistance performance under service speed,while the multi-speed optimization method is more effective for the resistance reduction and energy saving under both design speed and service speed.
purse seiner;bulb bow parameters investigation;wavemaking resistance;response surface model;multi-speed bulb bow optimization
U611.31+1
A
10.3969/j.issn.1673-3185.2015.04.007
2014-10-21网络出版时间:2015-7-28 17:25:22
中国舰船研究设计中心研发基金资助项目
刘成岗,男,1982年生,硕士,工程师。研究方向:渔船总体设计。E-mail:18627088387@163.com毛筱菲(通信作者),女,1962年生,教授。研究方向:船舶水动力性能和船型优化。E-mail:mxfzh@wut.edu.cn吴铭浩,男,1988年生,博士生。研究方向:船舶水动力性能优化设计。E-mail:wuminghao1988@gmail.com
