冲击与静载作用下地基响应的对比分析

罗嗣海，　吴周明，　桂勇（江西理工大学，.建筑与测绘工程学院；.应用科学学院，江西 赣州341000）

冲击与静载作用下地基响应的对比分析

罗嗣海a，吴周明a，桂勇b
（江西理工大学，a.建筑与测绘工程学院；b.应用科学学院，江西 赣州341000）

强夯与静载是加固地基的两种方式，但其作用的机理与过程是不同的.为了对比分析两种作用下地基土体的加固效果，考虑土体的材料与几何非线性，采用FLAC3D程序，建立强夯冲击和静载作用下地基的数值模型，对比分析地基土体内部位移场、应力场及密度等参数的变化规律.结果表明：产生相同的地表坑深所需的冲击应力峰值要明显高于所需的静载数值，冲击作用的竖向应力和竖向位移衰减快于静载作用，静载作用有效加固深度和地表加固宽度均要要大于冲击作用，冲击作用加固效果在浅层弱于静载作用、中部高于静载、深部两者趋同.研究成果深化了强夯与静载作用时地基内部响应的认识，探讨了分析强夯等动力荷载加固地基效果的新途径.

冲击；静载；数值分析；地基响应；对比分析

无论是强夯冲击还是静载作用都会使地基表面产生变形，对非饱和土及饱和粗粒土而言，地面变形主要表现为一定量的下沉坑.显然，坑是地基内部变形的外在表现，地基内土体压密变形程度与坑的深度密切相关.但强夯冲击和静载作用的机理与过程是不同的，强夯是瞬间给地基土体施加一个冲击荷载，冲击荷载产生应力波并迅速向土体深处传播，破坏土体结构或压缩土体产生残余变形，从而形成夯坑.静载作用则是一个缓慢作用的过程，随着时间的增长使土体内部产生变形，土体性质得到改善.

关于强夯和静力作用下地基响应的理论分析和数值计算早前已有一些研究［1-4］，近年又有进一步的研究［5-6］，但对比研究两者的规律则鲜见报道.本文考虑地基土体的材料与几何非线性，采用FLAC3D程序，建立强夯冲击和静载作用下土体的数值分析模型，对比分析地基土体内部位移场、应力场及密度等参数的变化规律，探讨分析强夯等动力荷载加固地基效果的新途径.

1　模型建立

1.1本构模型

土体的本构模型有许多，但在分析诸如强夯加固地基的冲击作用时，对于本构模型的采用目前还没有统一的做法.本文地基自重应力平衡计算采用各向同性弹性模型，强夯冲击特性和静载作用效果计算均采用德鲁克普拉格塑性模型［7］.

剪切屈服函数fs和张拉屈服函数ft表达式分别为式（1）和式（2）.

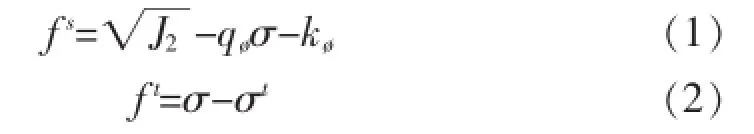
剪切塑性屈服势函数gs一般对应非相关联的流动法则，张拉塑性屈服势函数gt对应相关联的流动法则，分别为式（3）和式（4）所示.

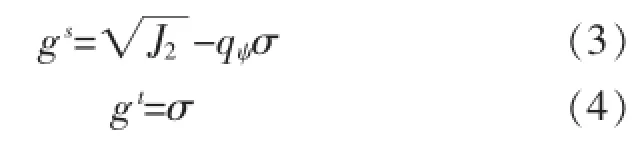
式（1）～式（4）中：J2和σ分别为应力偏张量的第二不变量与平均法向应力；σt为材料的抗拉强度，最大值σtmax=kø/qø；参数（3-sinø），kø=，其中ø为材料的内摩擦角，c为材料的内聚力；（3-sinΨ），Ψ为材料的剪胀角，qΨ=qø时变为相关联的流动规则.

1.2计算参数

1.2.1土质参数

为检验强夯等冲击荷载作用下土体数值模型的合理性，土质与工艺参数参考文献［8］：土干密度ρd取为1.96 g/cm3、土弹性模量E为14.4 MPa、土泊松比μ为0.2、土黏聚力c为18 kPa、土内摩擦角ø=剪胀角Ψ=30°.

1.2.2强夯荷载

夯锤落距h取10 m、锤体半径r取1.0m、锤重m分别取10 t、15 t、20 t和25 t.本文将强夯冲击过程简化为随时间变化的三角形动力荷载［9-11］加载到地基接触表面区域.最大接触应力、总接触时间和接触应力增大过程的时间分别由式（5）～式（7）计算.

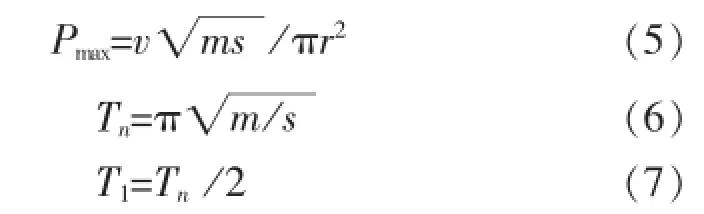
式（5）～式（7）中：动应力弹性常数s=2rE/（1-μ2）；夯锤达到地面的夯击速度；g为重力加速度，大小取为9.81 m/s2.

利用所建立的强夯数值模型和选取的相关参数，考虑塑性大变形特性，采用阻尼比为5%的局部阻尼［12］进行强夯单击冲击数值分析计算，计算结果与文献中工程实测结果基本相符，说明模型和程序的合理性.4种锤重作用下的强夯夯坑深度大小分别为 0.189 m、0.295 m、0.407 m和0.518 m，此处得到的夯坑深度即用作为静载作用所要达到的坑深.

1.2.3静载作用

静载作用数值分析模型利用强夯冲击数值模型除去动力属性参数后建立，静载垂直施加到冲击作用时的区域进行非线性塑性大变形计算直至稳定.显然，本文的计算方法与土力学［13］中的弹性和小变形假设条件下的地基在荷载作用时的最终沉降计算方法不同，同一静载作用时本文计算得到的沉降变形相对于弹性力学方法更大.

本文通过6次静载作用数值试算得到了相应的沉降坑深，并对静载大小和坑深进行拟合得到相关系数为0.998的多项式形式的近似公式（8）.

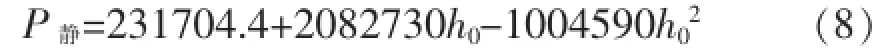
式（8）中：P静为地表静载大小（Pa）；h0地表坑深（m），0.146≤h0≤0.697.

由公式（8）可得到与需要分析的夯坑深度所对应的静载大小，并利用所得到的静载大小进行静载作用数值计算可以使地基表面形成与动力作用相同的坑深.

1.3网格离散

FLAC3D数值分析计算结果的精度与模型范围及网格划分密切相关，本文地基模型尺寸取20 m×20 m×12 m的空间区域，即地表区域面积为20 m×20 m、土层厚度为12 m，荷载作用区域为地表中心位置，采用笛卡尔直角坐标系统，原点坐标（0，0，0）位于模型底部中心处.采用Rad cylinder基本单元［9-10］对模型进行网格离散，并对荷载作用附近区域网格进行加密，网格划分情况如图1所示，地基水平方向和深度方向网格最小尺寸分别为0.25m和0.5 m，共划分为35557个节点和34560个单元.

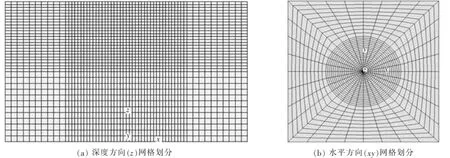
图1　地基模型网格划分情况

1.4边界条件

自重平衡和静载计算过程中约束模型底部边界x，y，z方向位移，约束模型4个侧面边界x，y，z方向位移，顶部边界为自由边界；强夯动力计算时将模型侧面边界和底部边界均设置为静态边界［9］以减弱动应力振动波在边界上反射后对地基内部加固的影响.

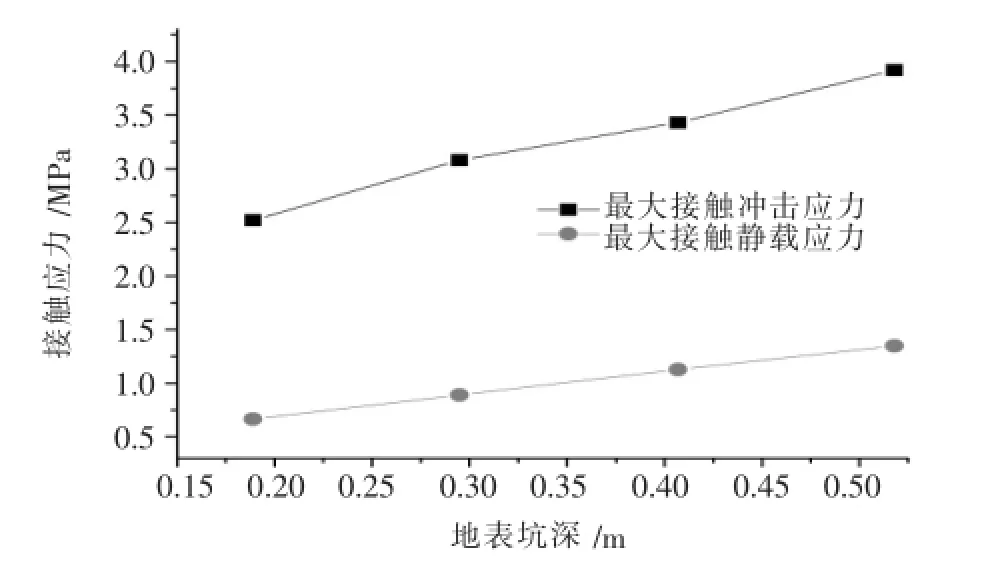
图2　接触应力峰值与地表坑深的关系

2　结果分析

提取强夯冲击及静载作用地基数值分析结果，对比土体内部竖向应力、竖向变形、土体密度、加固范围及位移场随土体深度、坑深的变化情况，在无特别说明的情况下的均为加载区域中心下方土体加载响应的对比.

2.1应力分析

2.1.1地表接触应力

地表接触应力峰值与地表坑深的关系如图2所示.从图2可以看出：在给定的夯坑深度范围内，无论是强夯冲击接触应力峰值还是最大接触静载应力与地表坑深均呈近似线性关系，且强夯冲击接触应力峰值要明显大于静载作用的接触应力，冲击应力随坑深的变化率也要略大于静载作用.

2.1.2地基内部竖向应力峰值

强夯冲击及静载作用竖向附加应力峰值和坑底应力的比值与土体深度的关系如图3所示，其中，图3（a）和图3（b）分别为坑深0.189m和0.518m时的变化关系图.从图3中可知在地基内部应力由接触应力随深度逐渐衰减，图3（a）中地基内部冲击作用时应力的衰减速率要快于静载作用时应力衰减速率，在较深处才出现静载比值大于冲击作用比值，图3（b）中两种加载方式时的应力在地基内部沿深度的衰减速率较为接近.不同坑深条件和土体深度处的两种加载方式的竖向应力变化情况有差异，地表坑深变形越大，强夯冲击与静载作用时应力衰减率差距越小，甚至出现静载衰减快于冲击作用，竖向应力与坑底应力比值相同的点的深度会更浅，应力的影响深度也会更深.考虑到强夯一般产生较大的地面变形，因此，似可推断强夯动应力分布应与静力作用下的有相似性.

2.2位移分析

2.2.1地基内部竖向位移

强夯冲击及静载作用下竖向位移和地表坑深的比值与土体深度的关系如图4所示，图4（a）和图4（b）分别为坑深0.189 m和0.518m时的变化关系图.图4中可知坑深相同时，地基内部会出现冲击作用与静载作用竖向位移相同的土层深度，此土层以上冲击作用产生的竖向位移大于静载作用引起的变形，该土层以下土体竖向位移静载作用效果要强于冲击作用，随着深度的继续增加两种加载方式竖向位移效果差距越来越小.对比图4（a）和图4（b）还可发现，坑深大时地基内部竖向位移相同的土层位置会更深，竖向位移影响的土体深度也会更大.

2.2.2地基变形范围

强夯地基加固范围有竖向加固深度和横向加固宽度，本文采用竖向变形值为地表坑深的5%作为单击有效加固深度的界定标准.图5为强夯与静载作用时有效加固深度与地面坑深的关系曲线，图6是坑深为0.189 m时强夯和静载作用地表竖向变形，负值表示变形方向向下.

图5中可以看出：静载作用时单击有效加固深度值要略大于强夯动力作用下的有效加固深度值，随着地表坑深的增大而增加，同时强夯冲击与静载作用的有效加固深度差距也逐渐缩小.可知虽然在地表形成的坑深相同，但冲击作用在地基深处的变形量小于静载作用产生的变形量，由于冲击作用在土体深处衰减迅速使得土体得不到永久压缩，而静载的长期作用可以使深层土体结构重新组合产生比动力瞬间作用更大的永久变形.

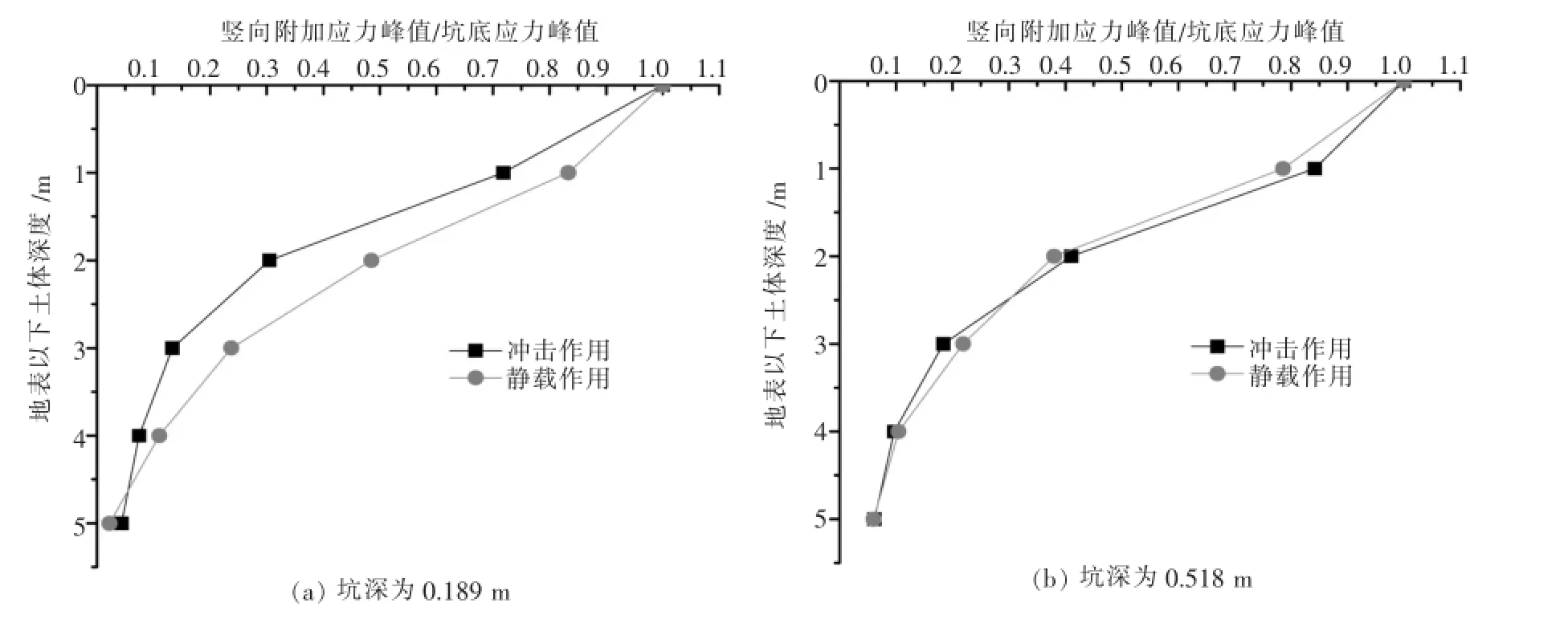
图3　竖向应力和坑底应力峰值的比值与深度的关系

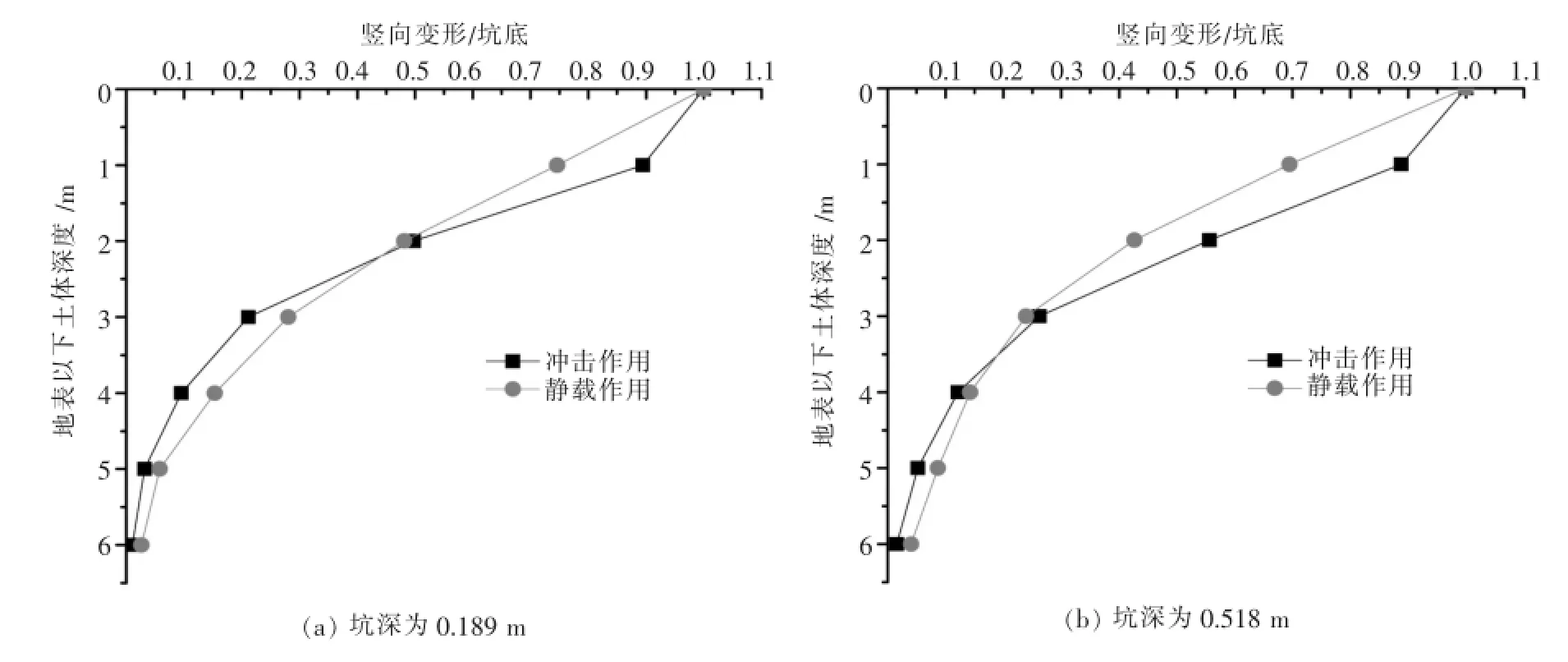
图4　竖向变形和坑深的比值与深度的关系

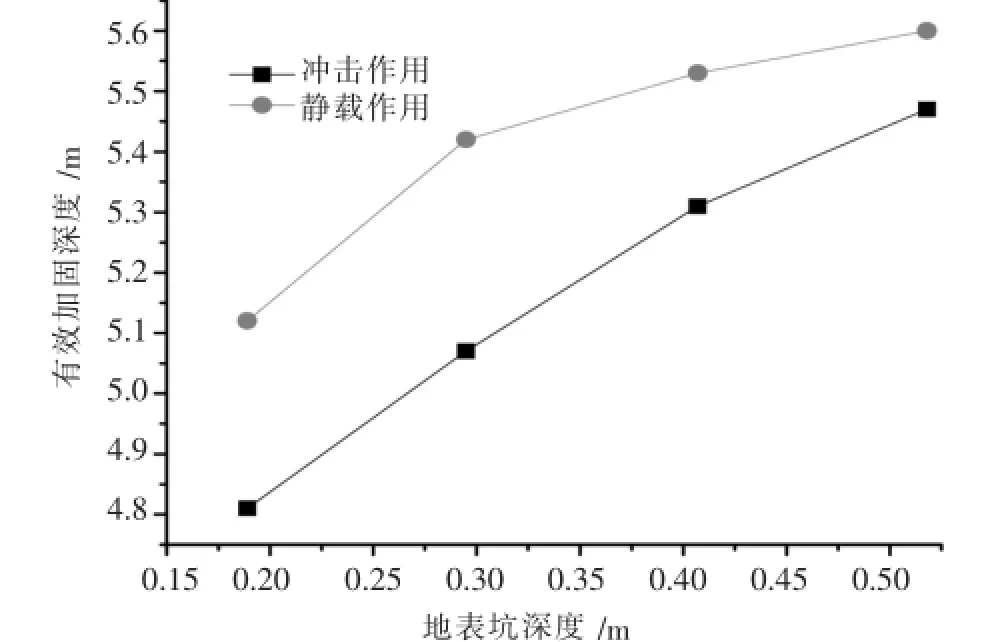
图5　有效加固深度与地表坑深的关系

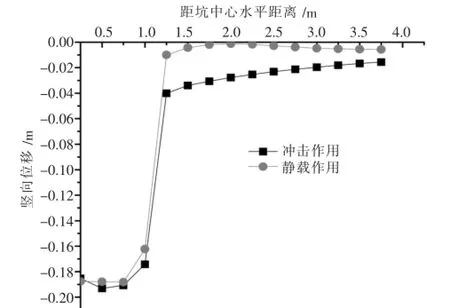
图6　坑深为0.189m时地表竖向变形

图6中可以看出：荷载作用区域范围内强夯冲击与静载作用下竖向变形变化相似，但在荷载作用区域的外侧，静载作用下土体的产生的竖向变形量要明显大于冲击作用，静载作用并没有使地表出现隆起，而动力作用下距作用区域边缘一定距离处土体有隆起的趋势；静载竖向变形的地表范围要宽于动力作用影响的范围，静载作用形成坑的体积也要大于动力作用下坑的体积，静载作用可以对加载区域周围一定范围的地表土体进行压密.

2.2.3加载区域下方位移场分布

为了更加直观全面的反映差异，进一步对地表坑深为0.189 m时地基沿深度方向位移场进行对比.编制转换程序将FLAC3D强夯单击冲击和静载计算结果导入tecplot专业绘图软件中绘制含有等值线的位移场图，如图7所示.图7（a）为竖向位移场等值线，数值单位为米，负值表示位移方向向下.图7（b）为横向位移场等值线图，正值表示位移方向向右，负值表示位移方向向左.图7（a）和图7（b）中，左半幅图为强夯作用位移场等值线，右半幅图为静载作用位移场等值线.

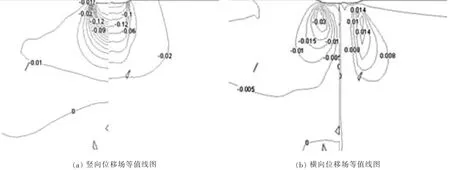
图7　位移场等值线图

从图7（a）中可知：强夯竖向位移场在地基内部为一椭球形分布，长轴沿深度方向，竖向位移场等值线以坑底边缘为起点向两侧和深度方向扩散，在夯锤作用区域外侧下方和夯点下一定深度会出现位移集中的现象，坑下会出现一压缩量不大的硬壳土层；静载竖向位移场在加载区域的空间范围主要呈圆柱形分布，竖向位移等值线在坑下随着深度的增大呈梯度均匀减少，坑外地表土体受中心区域沉降的影响会产生一定量的沉降.

从图7（b）中可知：由于此处荷载和地面变形量较小使得横向位移数值偏小，强夯冲击作用时，坑边缘处土体就会有水平位移集中产生，最大横向位移量约为0.03 m，加载区域下一定深度处土体由于受瞬间挤压会产生向两侧的位移，地表与坑中心一定距离处土体受强夯振动波的影响会有少量横向变形；静载作用时横向位移的出现主要是从地表以下某一深度处土体开始，地表几乎没有横向变形的产生，坑的正下方土体横向变形的程度很小，横向位移主要分布在坑边缘正下方土体处，最大横向变形量约为0.014m；另外还可以发现强夯作用的横向变形量、变形出现的深度和宽度都要大于静载作用.

2.3密度分析

地表发生某相同变形后，特定深度处强夯冲击与静载作用后土体密度比值与地表坑深关系如图8所示；地表发生特定变形后，某深度处强夯冲击与静载作用后土体密度比值与深度的关系如图9所示.图8和图9中：表层地基土体密度比值小于1，且密度比值随地表坑深增大而减小，即表层土强夯加密效果要弱于静载压密程度；超过一定深度以后土体密度比值大于1，且随地表坑深增大而增强，强夯冲击后的密度值要大于静载作用，但最大密度比值相差约为2%；同种地表坑深时浅层强夯加密程度小于静载作用，但随着深度的增加密度比值从小于1的值逐渐增大，在某一深度超过1后继续加大直至达到一个最大值，此处强夯加固效果最明显，再以后就会随着深度增加密度比值逐渐减小，直至在一定深度减小到1，此时密度值与夯前密度相比基本没有改变，不受地表荷载的影响.以上现象的主要原因可能有：强夯的动力作用使地基表层土受振动波的反射导致地表土体被振松，动力越大被振松的程度和范围也更大；动力在地表浅层一定深度处对土体产生主要影响且随地表变形增大影响增强，超过这一深度后影响减弱；静载作用时地表被压密的程度最大，土体深处被压密的程度逐渐减弱，但由于变形的均匀性使得压密程度弱于动力作用.

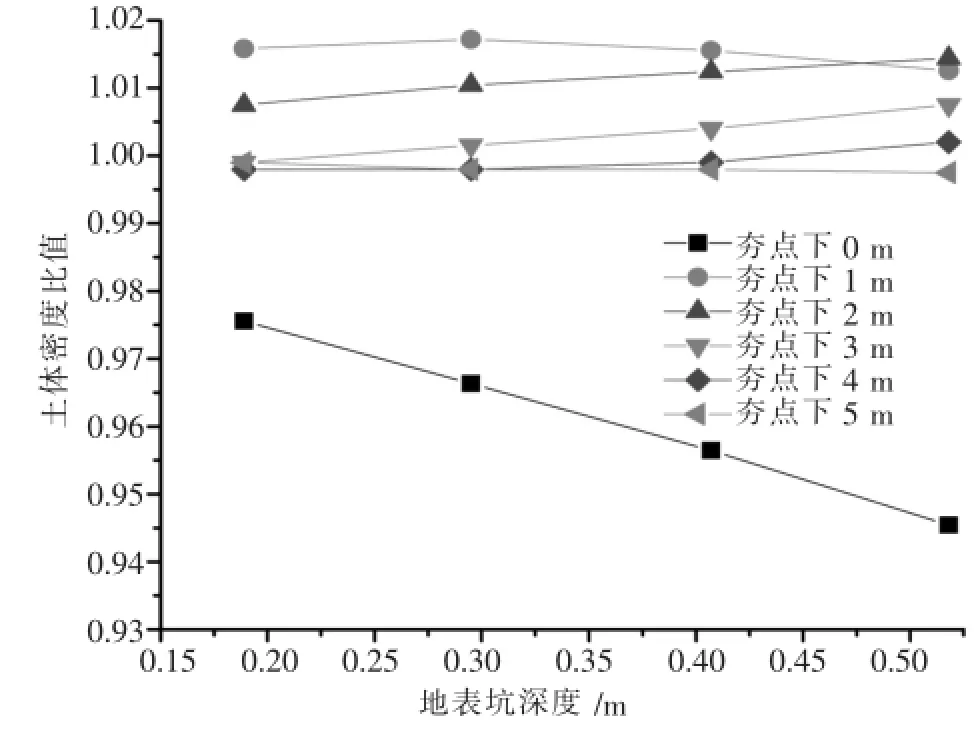
图8　土体密度比与地表坑深的关系

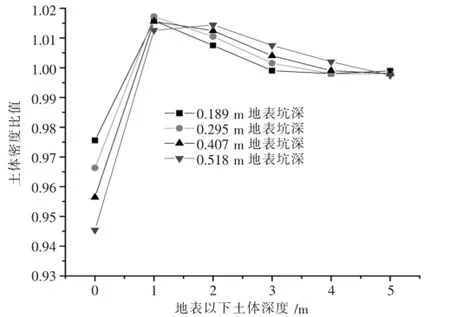
图9　土体密度比与深度的关系

3　结论

为对比分析两种作用下地基土体的加固效果，考虑土体的材料与几何非线性，采用FLAC3D程序，建立强夯冲击和静载作用下地基的数值模型，对比分析地基土体内部位移场、应力场及密度等参数的变化规律，得到如下结论：

1）产生相同的地表坑深，所需的冲击应力峰值要明显高于所需的静载数值；在考虑的夯深范围内，应力峰值与坑深近于线性关系，且冲击应力随坑深的变化率要略大于静载作用.

2）在地表变形较小时，动载作用的竖向应力衰减快于静载作用；地表变形增大时，两者趋于相近；夯坑中心点下的竖向位移冲击时的衰减速度快于静载时；坑深相同时，地基内部某深度处冲击作用与静载作用竖向位移相同，坑深越大时地基内部竖向变形相同的土层位置会更深，土体竖向变形的影响深度也更大.

3）圆形加载区域时强夯冲击地基竖向位移场近似为长轴延深度方向的椭球形分布，静载地基竖向位移场呈圆柱状分布，静载位移相对强夯类冲击位移随深度分布衰减更为均匀；相同地表变形时，静载作用有效加固深度和地表加固宽度均要要大于强夯冲击，但两者差距随地表坑深加大而变小.

4）相同地表变形时，强夯加固效果在浅层弱于静载作用，中部高于静载，深部两者趋同并与加固前变化不大.

［1］Poran C J，Kingsen H，Rodriguez JA.Impact behavior of sand［J］. Soils and Foundations.1992，32（4）：81-92．

［2］Chow Y K，Yong D M，Yong K Y，et al.Dynamic compaction of loose sand deposits［J］.Soilsand Foundation，1992，32（4）：93-106．

［3］孔令伟，袁建新．强夯时地基土的应力场分布特征及应用［J］．岩土工程学报，1999，20（3）：13-22．

［4］蒋鹏，李荣强，孔德坊．强夯大变形冲击碰撞数值分析［J］．岩土工程学报，2000，22（2）：222-226．

［5］胡焕校，罗玮.强夯作用下填土地基动力特性的数值模拟研究［J］.水资源与水工程学报，2012，23（4）：119-124.

［6］宋修广，周志东，杨阳，等.强夯法加固无黏性土路基的现场试验与数值分析［J］.公路交通科技，2014，31（3）：1-6，37.

［7］刘波，韩彦辉.FLAC原理、实例与应用指南［M］．北京：人民交通出版社，2005.

［8］王桂尧，胡振南，匡希龙．红砂岩路基强夯处理大变形数值模拟方法与效果分析［J］．岩土力学，2008，29（9）：2451-2456．

［9］陈育民，徐鼎平.FLAC/FLAC3D基础与工程实例［M］.北京：中国水利水电出版社，2009.

［10］彭文斌.FLAC23D实用教程［M］.北京:机械工业出版社，2007.

［11］李本平，陈燕顺，吴世明．用加载-卸载双线性模型分析强夯加固机理［C］//广州：第六届全国岩土力学数值分析与解析方法讨论会，1998.

［12］陆培炎，史永胜．岩土力学数值分析与解析方法［C］//广州:广东科技出版社，1998：469-474.

［13］高校土木工程专业指导委员会规划推荐教材.土力学［M］．2版.北京：中国建筑工业出版社，2005.

Contrastive analysis of the ground responses to impact and static load

LUO Sihaia，WU Zhouminga，GUIYongb

（a.School of Architectual and Surveying&Mapping Engineering；b.Faculty of Applied Science，JiangxiUniversity of Science and Technology，Ganzhou 341000，China）

Dynamic compaction and static load are two methods of ground stabilization，but their action mechanisms and processes are different.In order to analyze the consolidation effectof foundation soil under the two kinds of loads，thematerial and geometrical nonlinearity of the soil was taken into account，the FLAC3D program was adopted，the numerical model of foundation under the two kinds of loads was established，the change law of displacement field，stress field and density in the foundation soil was contrastively analyzed. Results show that the impact stress peak is apparently higher than that of the static load if they lead to the same pit depth；the attenuation velocity of the vertical stress and vertical stress of the impact effect are faster than that of the static load；the effective reinforced depth and breadth of the static load are greater than that of the impact effect；compared with the static load，the impact effect has a weaker consolidation effect in the superficial layer of the foundation，and greater in themiddle layer，the same in the deep layer.Research results deepen the knowledge of the response in the foundation under the dynamic compaction and static load，and discuss a new way of analyzing the consolidation effect of the foundation under the dynamic compaction.

impact；static load；numerical analysis；foundation responses；contrastive analysis

TU4

A

2095-3046（2015）05-0022-06

10.13265/j.cnki.jxlgdxxb.2015.05.005

2014-09-28

国家自然科学基金资助项目（50869002）；江西省自然科学基金资助项目（2008GZC0031）；江西省教育厅科技资助项目（［2007］210）

罗嗣海（1966-），男，博士，教授，博导，主要从事土力学与地基处理、环境岩土工程等方面的研究，E-mail:drsoil@163.com.