基于Memetic算法的无线传感网络覆盖优化

陈伟佳，关 健

(1.闽江学院 数学系，福建 福州350108;2.闽江学院 现代教育技术中心，福建 福州350108)

无线传感网络(WSNs)在军工和民用领域有着广泛的应用，如战场侦察、机械故障诊断、生物检测、家庭安防等［1］.由于无线传感网络通常应用在偏远无人值守的地方、电池更换不便，所以能耗控制是无线传感网络应用一个重要的研究方向.由于无线传感网络节点的高密度部署会带来大量的节点冗余，所以需要进行网络覆盖优化，从大量的传感节点中合理地选取一组节点进入工作状态，以保证区域充分覆盖.覆盖优化通过降低网络冗余，节省了能源并延长了网络的生存时间，是一种非常有效的能耗控制技术.

近年来，学者们陆续提出不同的智能优化算法求解无线传感网络的覆盖优化问题，如遗传算法［2-3］、粒子群算法［4-5］、鱼群算法［6］等.遗传算法(GA)具有搜索速度快、并行搜索能力强的特点，但是容易陷入“早熟”收敛和局部最优，不利于找到全局最优解.禁忌搜索算法［7］(TS)具有较强的“爬山”能力，在搜索过程中可以接受劣解，从而跳出局部最优解、转向其他区域搜索更好的解或全局最优解，但收敛速度慢，较难满足动态节点选取的实时性要求.

Memetic算法是一种将全局寻优与局部搜索相结合的算法框架［8］，兼顾广度和深度.基于Memetic算法框架，融合了遗传算法和禁忌算法，采用禁忌搜索算法作为局部搜索来增强遗传算法的搜索能力，并通过改进目标函数值的计算公式来提高算法的运算速度，同时利用随机和贪婪的策略构造较优的初始种群，仿真实验表明该算法是可行、有效的.

1 WSNs覆盖模型

假定在一个形状规则的二维监测区域中投放N个传感节点，各传感节点参数相同、坐标可知且相互独立.

定义1监测区域离散化为m×n个像素，则整个监测区域记为像素集A={(x，y)|x∈{1，2，…，m}，y∈{1，2，…，n}}，(x，y)为像素点.

定义2传感节点ci的坐标为(xi，yi)，有效感知半径为r，则该传感节点记为圆ci={xi，yi，r}，i∈{1，2，…，N}，所有节点记为C={c1，c2，…，cN}.

1.1 网络节点利用率

用布尔向量S={s1，s2，…，si，…，sN}标志各传感节点的状态，si=1表示节点ci处于工作状态，si=0表示节点ci处于休眠状态，则网络节点利用率

1.2 网络有效覆盖率

像素点(x，y)被传感节点ci覆盖的事件记为hi(x，y)，i∈{1，2，…，N}.当像素点(x，y)与传感节点ci圆心的距离不大于半径r且传感节点ci处于工作状态时，像素点(x，y)被传感节点ci覆盖，记P{hi(x，y)}=1，否则像素点(x，y)未被传感节点ci覆盖，记P{hi(x，y)}=0.事件hi发生的概率P{hi(x，y)}为一个二值函数:

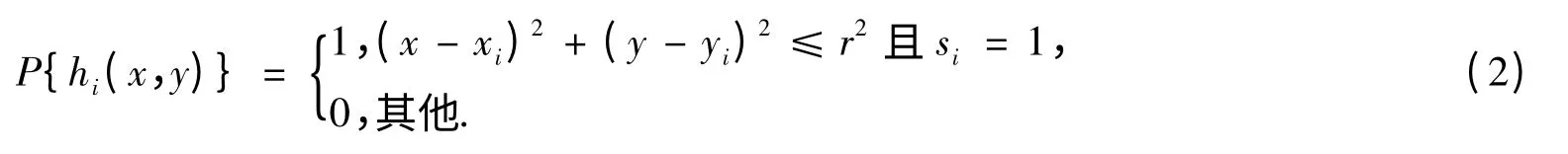
像素点(x，y)被节点集C中各节点覆盖的事件是相互独立的，则(x，y)被节点集C覆盖的概率

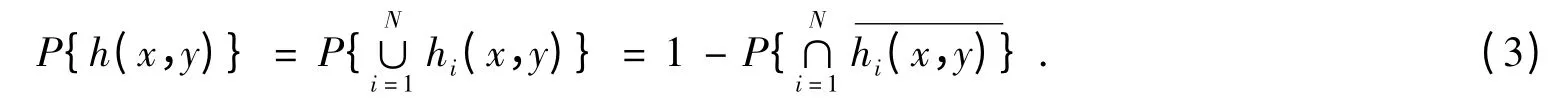
传感节点集C中工作节点所覆盖的像素点之和即为该节点集的覆盖区域，记为NA(C)，有

则网络有效覆盖率

1.3 覆盖优化数学模型

WSNs覆盖优化的目标是在保证网络有效覆盖率尽可能大的情况下努力减少节点的利用率，可以通过加权将有效覆盖率和节点利用率两个子目标函数转化为总体目标函数，作为算法求解的适应值，定义为

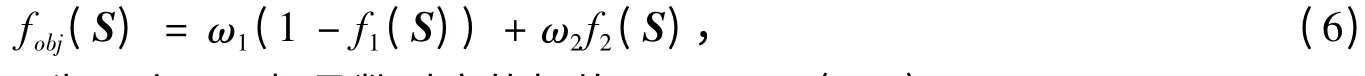
其中，S为节点状态的向量，ω1和ω2为两个子目标函数对应的权值，ω1，ω2∈(0，1)且ω1+ω2=1.

2 基于Memetic框架的覆盖优化算法

Memetic算法是群体全局优化算法和局部优化算法的结合.基于Memetic算法框架，采用遗传算法作为全局优化策略进行广度搜索，引入禁忌算法作为局部优化策略进行深度搜索.

算法1:

①利用算法2产生一个较优的初始种群，计算各个体的适应值;

②根据适应值，采用轮盘赌选法从群体中选出优胜的个体作为父母;

③随机选择一个交叉点，根据交叉率将父母在该点前的基因进行互换，生成两个新的子个体，期望父母将有益基因组合在一起遗传给子个体;

④根据变异率对子个体的个别基因进行变异，维持群体的多样性;

⑤用算法3对新的子个体进行局部优化;

⑥如果子个体的适应值优于种群中最差个体的适应值，用子个体替换最差种群中的个体，完成种群的更新，实现优胜劣汰;

⑦判断是否满足算法终止条件，若是，结束算法，否则转第②步.

Memetic利用遗传算法，选择质量较优的两个个体，通过交叉操作可将两个体的优良部分组合产生更加优秀的个体.但Memetic不局限于单纯的遗传算法，在每次交叉和变异后均进行局部搜索，及早剔除不良个体、优化种群结构，加快了算法的收敛能力.

2.1 编码和邻域结构

采用最简单的二进制编码表示问题的解，1表示传感节点处于工作状态，0表示传感节点处于休眠状态，即节点状态的标志向量S.邻域集采用1-变换的方法进行构造［9］，设一个解为S=(s1，s2，…，si，…，sN)，si∈{0，1}，i=1，2，…，N，则该解的邻域集为NS(S)={Si|Si=(s1，s2，…，1-si，si+1，…，sN)，i=1，2，…，N}，即仅有一个节点状态发生变换.

2.2 初始种群的构造

利用随机和贪婪的策略构造一个质量较好的初始种群.为了说明该贪婪策略的思想，做如下的定义:

定义3传感节点ci所覆盖的区域即为与ci圆心距离不大于r的像素集，记为

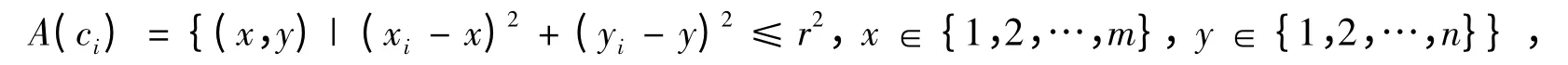
覆盖区域的大小记为|A(ci)|.

定义4传感节点ci的邻居即为与ci圆心距离不大于2r的节点集，记为

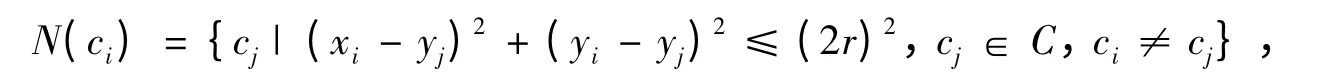
ci的邻居的个数记为|N(ci)|.

随机和贪婪策略的主要思想:首先，将所有N个传感节点处于休眠状态.其次，在N个传感节点中随机选择一个节点，从该节点和它的邻居节点中选择一个覆盖区域最大的节点处于工作状态.接着，将该覆盖区域最大的节点和与它距离小于一定值的邻居节点锁定.然后，继续从未被锁定的节点中随机选择一个节点，从该节点和它的邻居节点中选择一个覆盖区域最大的节点处于工作状态，锁定该覆盖区域最大的节点和它的邻居中与它距离小于一定值的节点，直到所有节点都被锁定，完成初始个体的构造.

算法2:

①初始化个体k的节点状态标志向量Sk={0，0，…，0}，所有N个传感节点未被锁定;

②从未被锁定的节点中随机选择一个节点ci，从ci和N(ci)中选择一个覆盖区域最大的节点cj，并让它处于工作状态sj=1;

③锁定cj与N(cj)中与cj距离小于一定值的节点;④判断是否还有未被锁定的节点，若有，转第②步，否则，初始个体的构造完成，转第⑤步;⑤判断是否达到种群所需的个体数，若是，转第①步，否则，初始种群构造完成，结束算法.

2.3 禁忌算法

禁忌算法具有强大的局部搜索能力，收敛速度快，最大特点是可以接受劣解，从而跳出局部最优，引入禁忌准则来避免迂回搜索，并通过特赦准则来赦免一些被禁忌的优良解，进而探索更优的解［10］.

算法3:

①初始化算法参数，选择一个个体的状态标志向量作为初始解S0;

②令当前解Snow=S0，全局最优解Sbest=S0，置禁忌表为空;

③构造Snow的邻域解集NS(Snow)并计算各邻域解的适应值，如果禁忌表满了，则将表中最早保存的解移除;

④按适应值从高到低对邻域解进行排序为{S1，S2，…，SN}，令i=1;

⑤特赦准则判断，如果邻域解Si的适应值大于全局最优解Sbest的适应值，则将Si对应Snow状态发生变换的节点加入禁忌表，Snow=Si，Sbest=Si，转第③步，否则转第⑥步;

⑥禁忌准则判断，如果邻域解Si对应Snow状态发生变换的节点不在禁忌表中，转第⑦步，否则，i=i+1，转第⑥步;

⑦将Si对应Snow状态发生变换的节点加入禁忌表，Snow=Si，如果邻域解Si的适应值大于全局最优解Sbest的适应值，则Sbest=Si，转第⑧步，否则直接转第⑧步;

⑧判断是否满足算法终止条件，若是，则输出全局最优解Sbest，结束算法，否则转第③步.

2.4 改进的适应值计算

禁忌算法对一个解的所有邻域进行搜索，需要计算N次目标函数值.然而，利用式(4)和式(5)对目标函数中的网络有效覆盖率进行一次计算，所需时间为O(N×m×n).因此，对一个解进行一次邻域搜索所需时间为O(N2×m×n)，耗费的时间代价非常大.根据邻域的结构特点可知，解S与邻域解Si对比只有一个节点ci的状态发生了变换，邻域解Si的适应值可由解S的适应值加上发生变换带来的适应值差异Δ，改进适应值计算公式为

关于适应值差异Δ，主要需考虑ci所覆盖的区域A(ci)被ci的邻居N(ci)中所有工作的节点联合覆盖的情况，记为NA(N(ci))，有

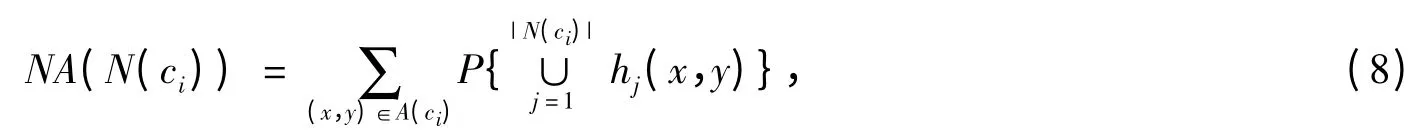
其中，hj(x，y)为像素点(x，y)∈A(ci)被节点cj∈N(ci)所覆盖的事件.

如果ci的状态由工作变为休眠，有

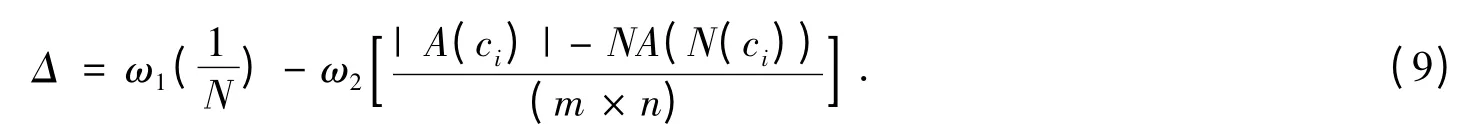
如果ci的状态由休眠变为工作，有

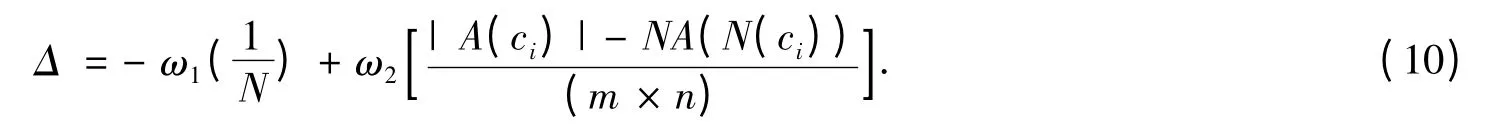
由式(9)可知，利用改进的适应值计算公式进行一次邻域搜索所需时间为O(N×|N(ci)|×|A(ci)|)，而|N(ci)|＜N，|A(ci)|≪(m×n)，大大节省了运算时间.

3 仿真实验与分析

实验环境参照文献［4］设置:监测区域为100 m×100 m，将其离散为100×100个像素，节点感知半径为11.5 m.首先，确定性部署39个节点以正六边形结构最优化分布于监测区域，如图1所示.然后，再随机部署61个节点于该监测区域，如图2所示.适应值函数式(7)中，ω1=0.1，ω2=0.9.

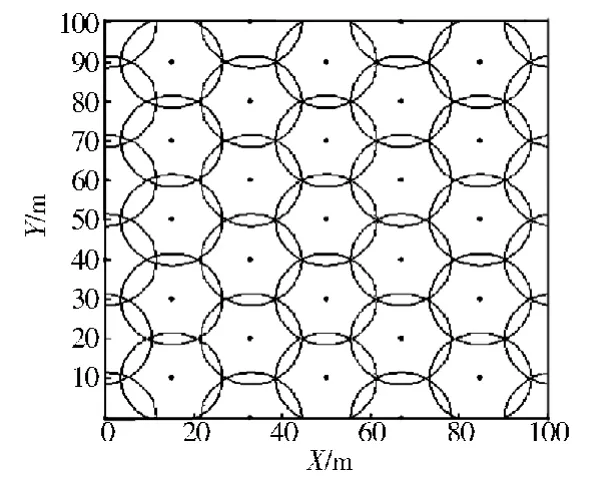
图1 最优节点分布Fig.1 The optimal distribution of nodes

图2 初始节点分布Fig.2 The initial distribution of nodes

Memetic算法的参数设置如下:种群数量为5，交叉概率为0.8，变异概率为0.05，达到100次迭代终止迭代，TS的最大迭代次数为20，禁忌长度为10.图3中(a)、(b)、(c)分别为Memetic算法优化过程第1 s，3 s和5 s的节点分布情况.整个优化过程节点分布逐步趋于最优，第5 s时的节点分布图3(c)已经非常接近图1中的最优节点分布，覆盖率为99.76%，节点利用率为39%.结果表明，Memetic算法能快速收敛于优秀解、达到优化覆盖的目的，是一种有效的无线传感网络覆盖优化算法.

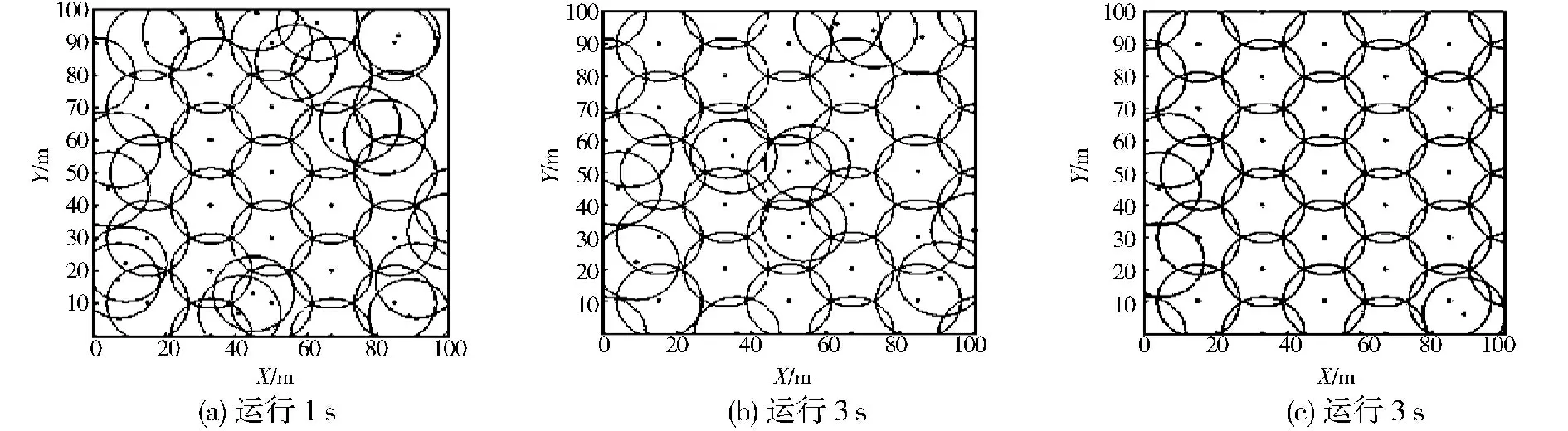
图3 M emetic优化过程的节点分布Fig.3 The distributions of nodes in the optim ization process of Memetic

为了验证算法的优越性，在相同的仿真环境下，采用遗传算法和禁忌算法对无线传感网络覆盖进行优化对比，仿真结果如图4所示.从图4中可以看出，在相同的运行时间下，Memetic算法得到的目标函数值高于GA和TS.为获得超过0.95的目标函数值，Memetic算法需要运行的时间小于5 s，而GA算法和TS算法需要运行的时间分别高于50 s和60 s.因此，3种算法中，Memetic算法的性能优于其他两种算法，是一种性能更优的覆盖优化算法.

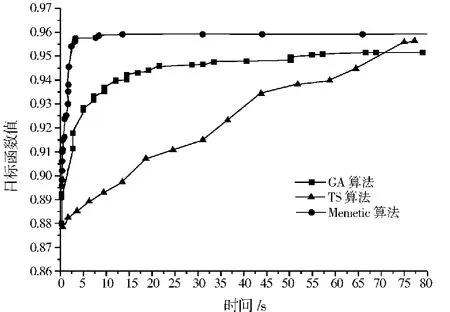
图4 目标函数值随运行时间的变化曲线Fig.4 The change curve of objective function value and time

4 结语

提出了基于Memetic算法的覆盖优化.算法考虑了解的质量和多样性，利用相邻节点间的区域覆盖关系，提高了目标函数值的计算速度.与遗传算法和禁忌算法对比，Memetic算法的收敛结果好、速度快，在保证尽可能高的网络覆盖率下减少了节点的利用率，有效解决了高密度部署的WSNs工作节点集的选取问题.

［1］Liu Y，Suo L，Sun D，et al.A virtual square grid-based coverage algorithm of redundant node for wireless sensor network［J］.Journal of Network and Computer Applications，2013，36(2):811-817.

［2］贾杰，陈剑，常桂然.无线传感器网络中基于遗传算法的优化覆盖机制［J］.控制与决策，2007，22(11):1289-1292.［3］林梅金，苏彩红，王飞.无线传感器网络覆盖优化算法研究［J］.计算机仿真，2011，28(3):178-181.

［4］林祝亮，冯远静.基于粒子群算法的无线传感器网络覆盖优化策略［J］.计算机仿真，2009，26(4):190-193.

［5］沈海洋.基于遗传PSO的无线传感网络覆盖优化算法研究［J］.微电子学与计算机，2013，30(3):148-151.

［6］周利民，杨科华，周攀.基于鱼群算法的无线传感网络覆盖优化策略［J］.计算机应用研究，2010，27(6):2276-2279.

［7］胡峻浩，刘兴长，谈昨非.基于禁忌算法的无线传感器网络PEGASIS算法改进［J］.后勤工程学院学报，2013，29(4):91-96.

［8］魏心泉，王坚.多目标资源优化分配问题的Memetic算法［J］.控制与决策，2014，29(5):809-814.

［9］林耿，朱文兴.多维背包问题的变邻域填充函数算法［J］.福州大学学报:自然科学版，2012，40(1):14-21.

［10］刘霞，齐欢.最小-最大车辆路径问题的禁忌搜索算法［J］.系统工程，2007，25(1):49-51.