轴承微极流体弹流润滑的三维数值解
2015-08-27路遵友王海群
路遵友,王海群,马 涛
(1.山东轻工职业学院 机电工程系,山东 淄博255300;2.山东东岳集团,山东 淄博256401;3.河南工程学院 机械工程学院,河南 郑州451191)
微极流体是一种极性流体,是由固体颗粒和黏性基液组成的悬浮液体,这些颗粒具有单独的质量和速度.微极流体的研究考虑了润滑剂的内部微观结构,保持了固体颗粒的微运动,因而具有非牛顿流体的特性.以往的润滑研究证明了滚动轴承在旋转过程中如使用加入少量高分子添加剂的微极性润滑油可以改善润滑性能,所以微极流体润滑被越来越多的学者重视.1982年,Singh和Sinha[1]在理论上推导了广义的微极流体问题的Reynolds方程,但未能给出数值求解过程和程序运行结果,本研究在此基础上给出滚动轴承点接触和线接触微极流体弹流润滑的三维数值求解方法,并给出了各自的运行结果.
1 微极流体弹流润滑的Reynolds方程
1.1 连续方程

式中的u,v,w分别为微极流体在x,y,z方向上的速度分量,x,y,z方向分别代表轴承滚动方向的切线方向、轴承的轴向方向和竖直方向.
1.2 平衡方程
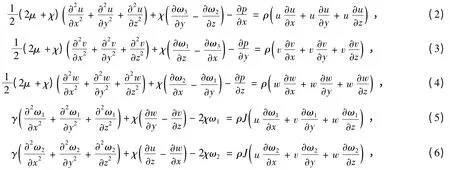
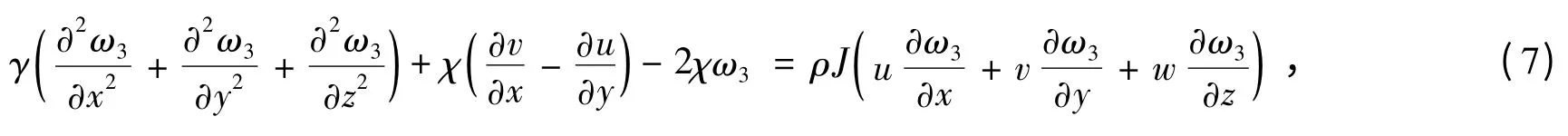
式中的ω1,ω2,ω3分别为微极流体在x,y,z方向上的转动角速度;μ为微极流体的黏度;χ为微极流体的旋转黏度;ρ为润滑剂密度;J为微极流体的惯性系数;γ为微极流体的材料常数.
1.3 推导后的Reynolds方程
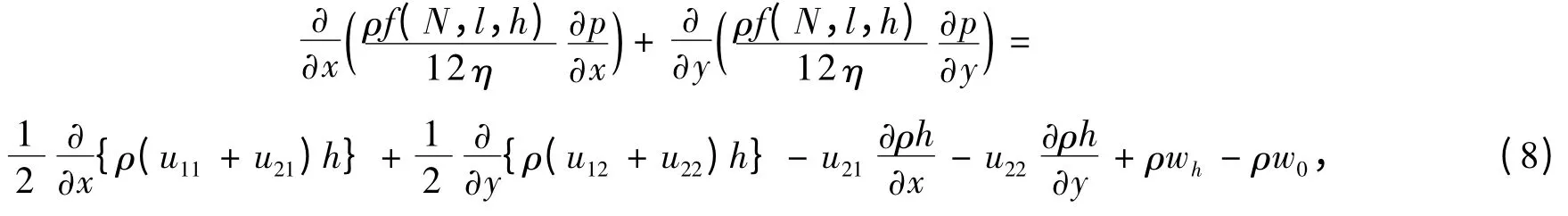
式中,N为微极流体耦合系数,l为微极流体的特征长度,h为润滑膜膜厚,η为润滑剂黏度,u11和u12分别为y=0时微极流体在x和y方向上的速度分量,u21和u22分别为y=h时微极流体在x和z方向上的速度分量,w0和wh分别为y=h和y=0时正常表面速度分量.另外,式中的f(N,l,h)=h3+12l2h-6Nlh2coth,其中coth为双曲余切函数.
2 数值解法
针对点接触和线接触的特点,对方程进行分析,利用文献[2]给定的边界条件,考虑了弹性变形.为简化计算,对Reynolds方程无量纲化后,采用有限差分法对方程进行离散[3-4],并用超松弛迭代方法对Reynolds方程求解并达到了良好的收敛效果.迭代求解的收敛条件为10-6,其中和分别为第K次和第K+1次迭代后的压力值,∑表示从1到K+1次的数值求和.数值求解流程如图1所示.
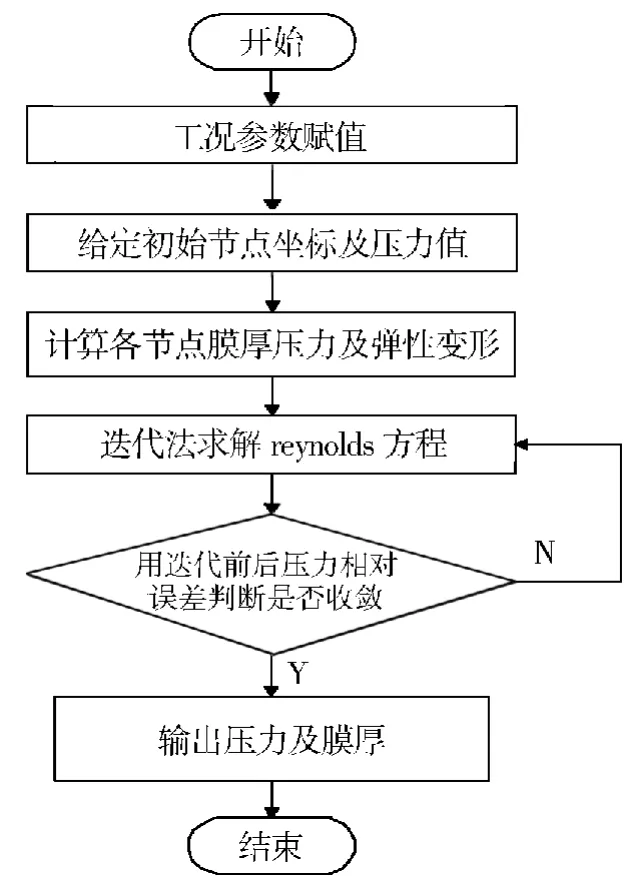
图1 数值求解流程Fig.1 Flow chart of numerical solutions
3 运行结果
利用Matlab软件进行编程求解,首先对工况参数进行预赋值.
3.1 线接触参数赋值及运行结果
程序中主要参数的预赋值为-4.0≤X≤1.5(x的无量纲化范围),-1.0≤Y≤1.0(y的无量纲化范围),外加径向载荷w=1.0×105N,综合弹性模量E=2.2×1011Pa,润滑油初始黏度η0=0.05 Pa·s,当量接触半径R=0.05m,接触面的平均速度为1.6 m/s,迭代次数N=130,其他参数按照常规润滑理论中的要求进行赋值.通过程序模拟计算,得到线接触微极流体弹流润滑二维压力分布和膜厚分布情况曲线,数值上与传统的理论研究相吻合,如图2和图3所示.
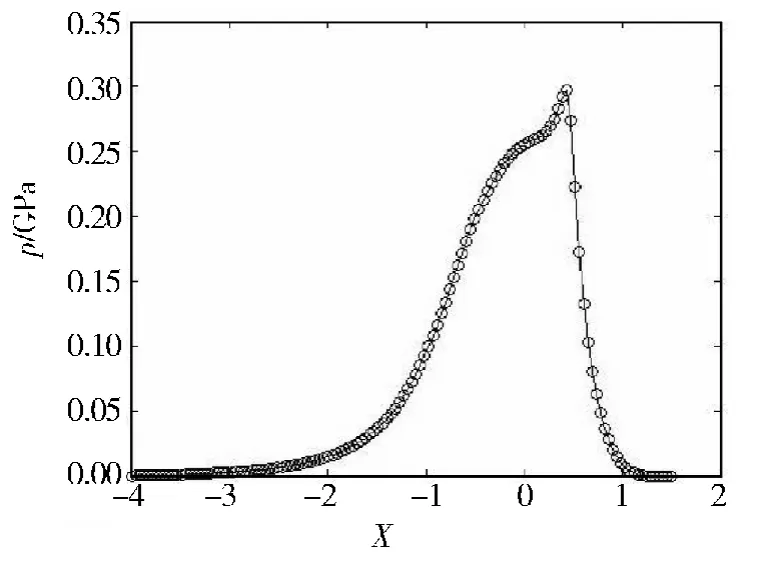
图2 线接触压力分布Fig.2 Pressure distribution of line contact
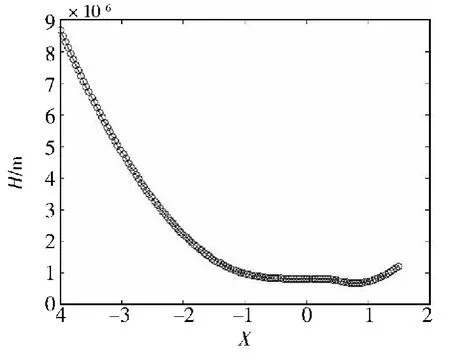
图3 线接触膜厚分布Fig.3 Film thickness distribution of line contact
同样,用程序得到了三维压力和膜厚分布情况,如图4和图5所示.
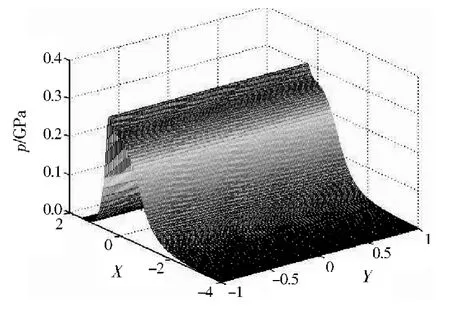
图4 线接触三维压力分布Fig.4 Three-dimensional pressure distribution of line contact
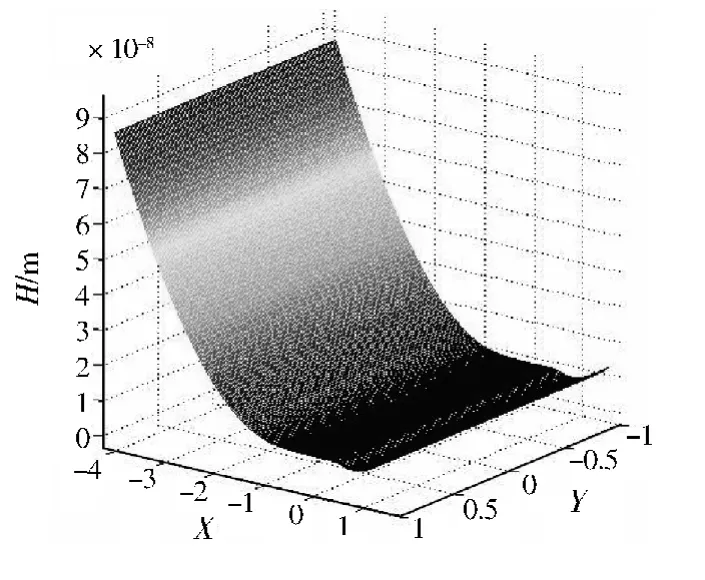
图5 线接触三维膜厚分布Fig.5 Three-dimensional film thickness distribution of line contact
3.2 点接触参数赋值及运行结果
程序中主要参数的预赋值为-2.5≤X≤1.5(x的无量纲化范围),-2≤Y≤2(y的无量纲化范围),外加径向载荷w=0.8×109N,综合弹性模量E=2.2×1011Pa,润滑油初始黏度η0=0.05 Pa·s,当量接触半径R=0.05 m,接触面的平均速度为1.0 m/s,迭代数为N=65,其他参数按照常规润滑理论中的要求进行赋值.通过程序模拟计算,得到点接触微极流体弹流润滑二维膜厚(Y=0处)分布和压力(Y=0处)分布情况曲线,数值上与传统的理论研究一致,如图6和图7所示.
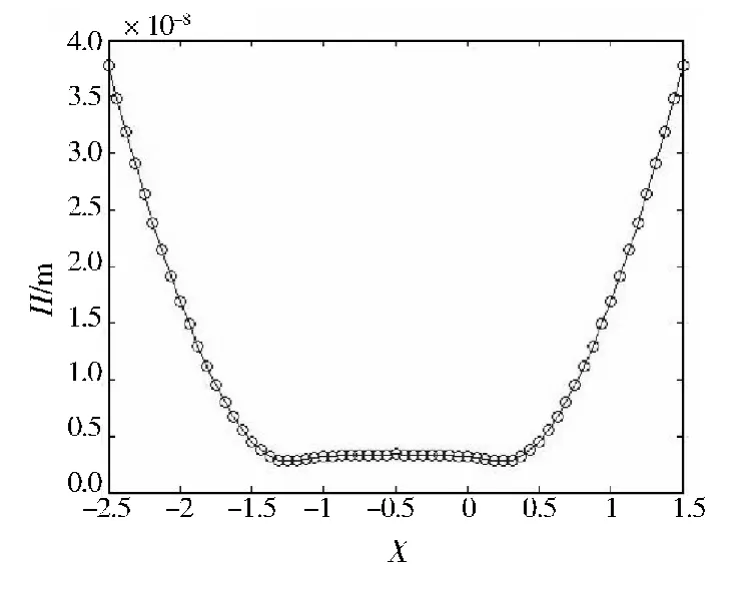
图6 点接触在Y=0处膜厚分布Fig.6 Film thickness(Y=0)distribution of point contact
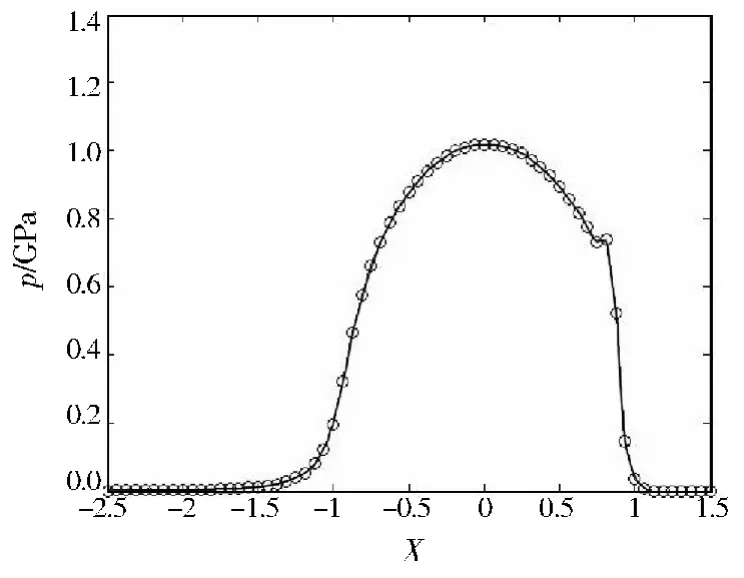
图7 点接触在Y=0处压力分布Fig.7 Pressure(Y=0)distribution of point contact
同样,用程序得到了三维膜厚和压力分布情况,如图8和图9所示.
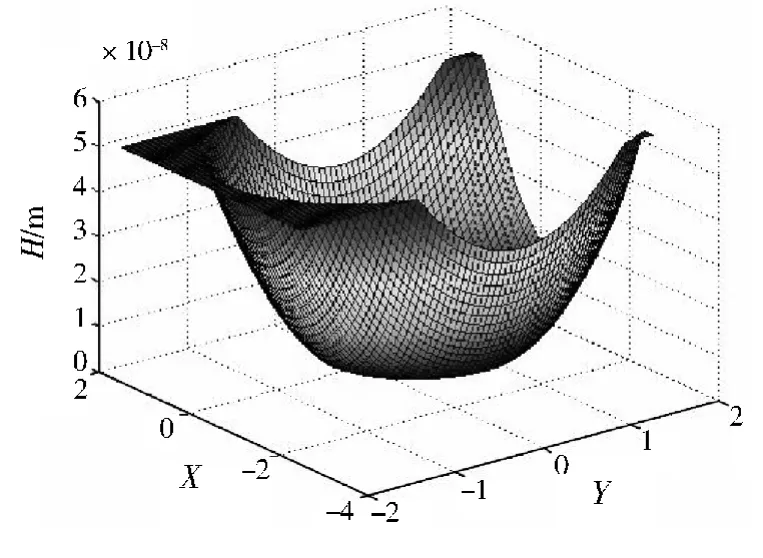
图8 点接触三维膜厚分布Fig.8 Film thickness distribution of point contact
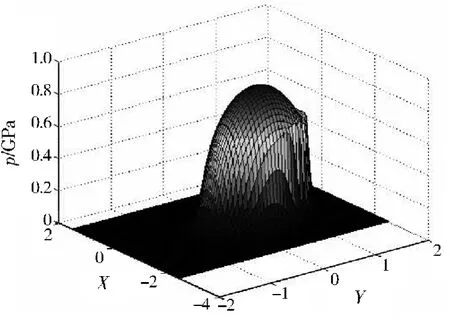
图9 点接触三维压力分布Fig.9 Pressure distribution of point contact
4 结语
针对给定的微极流体弹流润滑的Reynolds方程,通过软件编程实现了数值求解方法,给出了点接触和线接触微极流体弹流润滑的三维压力、膜厚的分布图像.较以往文献[5-8]中给出的二维结果,本研究创新性地给出了更加形象直观的三维压力和膜厚的分布情况,而且更加贴近实际,为今后的相关研究提供了一定参考.
[1]Singh C,Sinha P.The three-dimensional Reynolds equation for micro-polar-fluid-lubricated bearings[J].Wear,1982,76(2):199-209.
[2]温诗铸,杨沛然.弹性流体动压润滑[M].北京:清华大学出版社,1992.
[3]温诗铸,黄平.摩擦学原理[M].4版.北京:清华大学出版社,2012.
[4]黄平.润滑数值计算方法[M].北京:高等教育出版社,2012.
[5]卢立新,张和豪.固液两相流体弹流润滑研究[J].润滑与密封,2006(11):47-49.
[6]张俊岩,王晓力.微极性流体润滑的挤压膜轴承特性研究[J].北京理工大学学报:自然科学版,2009,29(9):771-777.
[7]丁雪兴,程香平,杜鹃,等.机械密封混合摩擦微极流体弹性润滑的数值模拟[J].兰州理工大学学报,2008,34(4):70-76.
[8]伟政,俞树荣,丁雪兴,等.螺旋槽干气密封稳态微尺度流动场的动压计算[J].兰州理工大学学报,2006,32(6):72-75.
