“三重联系”的数学课堂教学设计之意涵、作用与要求

【摘 要】为提高数学课堂教学的实效，应在理解与把握“基于‘三重联系的数学课堂教学设计”意涵的基础上，充分发挥其有利于提高学生数学学习的兴趣、有利于提升学生数学有意义记忆的水平、有利于发展学生数学联想的能力等作用，并努力做到它所要求的整体系统、动态生成与以学生为本的目标。

【关键词】三重联系;教学设计;意涵;作用;要求

【中图分类号】G633.6 【文献标识码】A 【文章编号】1005-6009（2015）26-0021-02

【作者简介】徐文彬，南京师范大学课程与教学研究所（南京，210097）教授、博士生导师。

数学的最大特征是其高度的抽象性、严密的逻辑性和广泛的应用性。而大多数接受过基础教育（甚至高等教育）的成人对数学的印象与此不无一致：好枯燥、好乏味、（好似）无处不用数学。为解决此类“一致性矛盾”，《义务教育数学课程标准（2011年版）》已为我们指明了努力方向：数学课堂教学应让学生“体会数学知识之间、数学与其他学科之间、数学与生活之间的联系……”那么，我们应如何基于“三重联系”来设计课堂教学呢？

一、基于“三重联系”的数学课堂教学设计之意涵

“基于‘三重联系的数学课堂教学设计”主要有以下几项意涵：首先，应在充分理解所教授的数学学科内容领域（譬如，数与代数）内部各部分知识之间的内在关联性的基础上，分析该内容领域与其他内容领域（譬如，图形与几何、统计与概率、综合与实践）之间的“外部”关联性;其次，应在充分了解当下儿童的实际生活和社会发展状况的前提下，探讨所教授的数学学科内容领域与其所存在的各种现实的或潜在的关系;第三，应在充分知晓所教学生所学其他学科内容的基础上，研究所教授的数学学科内容领域与其他学科之间的关系;最后，应结合所教学生的年龄特征与实际情况，有针对性地设计相应学科内容领域的学习目标或教学目标、学习活动或教学活动、学习评价或教学评价，并始终关注它们之间的相互协调与一致性问题。

二、基于“三重联系”的数学课堂教学设计之价值

兴趣是最好的老师，而唯有联系学生当下“深陷、遭遇的”生活实际与社会实践，才有可能引发学生的注意，以至培养学习的兴趣、思考的习惯。数学历来被认为是中学最为“枯燥、乏味的”一门课程，不少学生深受“努力学、学不好、好难学、学不会……”的境地，以致患有“数学恐惧症”。而解除这些学生的痛苦，并提高其他学生学习数学的兴趣的良方之一便是，把数学与他们的实际生活与社会实践联系起来，思考并设计课堂教学。

机械记忆是最不牢靠的，而有意义的记忆则是可以长久储存的。数学常常给人以“几何难、代数繁、三角公式背不完”的刻板印象。这其中的缘由之一可能就是我们的数学教学，既缺乏数学各领域内部的联系，又少有各领域之间的内在关联。因此，破除这一“刻板印象”的方法之一就是，就中学数学的所有内容来思考其各领域内部以及各领域之间的本质联系，并设计其课时新授、单元复习、阶段复习（包括期中、期末）以及相应的练习或习题课与试卷讲评的教学设计。

任何事物都是质与量的统一体，任何“没有质的量”与“没有量的质”都是不可想象的。而数学是只研究事物的量，不涉及事物的质。所以，数学学科是关于“纯粹思想事物”的知识体系，抽象性极高、逻辑性极强。但是，数学的发生、发展和应用，一刻也没有离开过其他学科的滋养。曾经，物理的“养育之功”最大;现在，几乎没有哪一门学科不能给予数学以“营养”。因此，仅就“历史重演律”而言，也需要我们把数学与其他学科联系起来思考并设计课堂教学，培养与发展学生的数学联想能力。

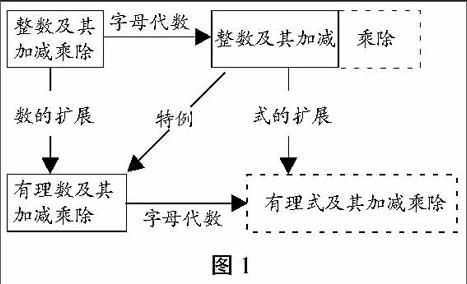
譬如，当学生对相对独立的数学知识单元的数学事实积累到一定的程度时，就应鼓励、引导、帮助学生自主地通过组织化的手段获得逐步系统化的知识，形成或优化相应的认知结构（知识结构的内化）。例如，在学完《整式》这一单元之后，就应创设情境促使学生主动地对下列知识结构（见图1）进行内化。这里既要强调整数与整式、有理数与有理式的共同点，也要注意其区别。

图1

（注：要在虚线框内的内容还没有学习前进行组织化。）

由图1我们约略可知“整数→有理数”——“整式→有理式”的结构，这里不仅有提升学生数学有意义记忆水平的考虑，更有培养与发展学生数学联想能力的设计，甚至还有培养学生数学学习兴趣的深意。

三、基于“三重联系”的数学课堂教学设计之要求

首先，“基于‘三重联系的数学课堂教学设计”要求我们的教学设计应是整体系统的。其一，应把数学课堂教学置于学校教育当中来考虑;其二，应把初中数学课堂教学置于义务教育阶段乃至基础教育阶段（包括幼儿园与高中）数学教育当中来考虑;其三，应整体地考虑初中数学教育中四大内容领域的课堂教学;其四，应系统地考虑各内容领域的课堂教学设计;其五，应系统地考虑每一个内容领域中各年级各学期的数学内容的课堂教学设计;其六，应置“课时教学备课”于单元教学设计当中来考虑。譬如，初中生常常会在学习“运用一元一次方程解决实际问题”时仍然习惯于运用“算术方法”来求解，何以会如此呢？小学“归类解文字应用题”之故也。如果我们不能“回到小学”，我们甚至连这类问题也无法解释，何谈解决？

其次，“基于‘三重联系的数学课堂教学设计”要求我们的教学设计应是动态生成的。尽管任何形式的课堂教学设计都有预设与生成，但是，“基于‘三重联系的数学课堂教学设计”更关注动态生成。其一，“三重联系”甚至就其中的“数学知识之间的联系”也不仅仅是确定不变的逻辑关系，更不是“史实”似的铁律关系，而是社会理解的，深蕴人文性;其二，就当下儿童数学学习的背景资源而言，我们教师可能无论如何也无法穷尽其所有，这便给我们带来了极大的挑战，教师既需要对此保持敏感，又需要果断决策。

再次，“基于‘三重联系的数学课堂教学设计”要求我们的教学设计应是以学生为本的。“以学生为本”不能仅仅局限于学生的学习结果（尤其是学习成效）或学习过程（尤其是学习活动），而应更多地关注他们对自己的学习过程与学习结果的主观感受，并据此来处理或协调课堂教学中的各种对称关系：课前预设与课堂生成，教师主导与学生自主，教学进程与学习进程，课本知识与学生经验，学科思维与学生思维，学生的个体差异和个别差异及其给予教师的启发，学生的学习结果和学习过程及其给予学生的主观感受，等等。

上述所谓“基于‘三重联系的数学课堂教学设计之要求”是相对于我们惯常的课堂教学设计而言的。如果“惯常的”已变成“怪异的”，而“基于‘三重联系的数学课堂教学设计”已变成惯常的，那么，上述所谓的要求都将不成为问题，这也正是我们所期待的。

【参考文献】

[1]义务教育数学课程标准（2011年版）[S].北京：北京师范大学出版社，2011.

[2]徐文彬.关于数学文化视域中数学教学的若干思考[J].课程·教材·教法，2012（11）.

[3]徐文彬.如何认识《义务教育数学课程标准》中的三重联系[J].江苏教育：小学教学，2013（02）.

[4]徐文彬.基于“三重联系”的课堂教学设计——以《一元一次方程》单元复习为例[J].江苏教育：中学教学，2013（05）.

[5]徐文彬.关于数学文化视域中数学学习的构想[J].数学教育学报，2014（05）.

【基金项目】2011年度江苏省教育科学规划重大课题（A/2011/08）：基础教育课程改革重大理论与实践问题的深化研究