古塔变形模型

徐翠翠

（陕西铁路工程职业技术学院，陕西　渭南714000）

古塔变形模型

徐翠翠

（陕西铁路工程职业技术学院，陕西渭南714000）

本文通过圆球曲面拟合和多元线性回归等方法建立了古塔中心的数学模型，求出了古塔各层中心坐标。

圆曲线拟合；圆球曲面拟合；多元线性回归

一、问题重述

某古塔已有上千年历史，是我国重点保护文物。管理部门委托测绘公司先后于1986年7月、1996年8月、2009年3月和2011年3月对该塔进行了4次观测。

试建立确定古塔各层中心位置的数学模型，并列表给出4次测量古塔各层中心坐标。

二、问题分析

由于古塔年久已经变形，要确定中心，就要每层拟合一个对应层测点总体距离最小的圆，而圆心即为中心，因此确定拟合圆是关键，而由于古塔有可能发生倾斜，测点不一定在一个水平面上，所以首先通过多元线性回归确定每一层所在的平面方程，其次拟合该层测点数据的圆球方程，则平面与圆球的相交曲线即为所求拟合圆，再通过向量空间的几何知识建立线性方程组，求解拟合圆圆心，得到各层中心坐标。

三、模型假设

1.假设古塔每一单层（两个相邻中心）中间没有弯曲、扭曲等变形情况，只可能发生倾斜变形；

2.假设弯曲、扭曲等变形情况只发生在层与层之间；

3.假设八个观测点均在塔的外墙处；

4.假设每一层古塔的测点坐标均在该层的塔板面上。

四、符号说明

（Xi，Yi，Zi）表示古塔第i层的中心坐标；（xi，yi，zi表示古塔第i层的圆球曲面的球心坐标；

（xij，yij，zij表示古塔第i层第j个观测点坐标；

Ri表示古塔第i层拟合圆的半径；

rj表示古塔第i层拟合圆球曲面的半径；

Oi表示古塔第i层拟合圆的圆心。

五、模型的建立与求解

表3　

当古塔建筑测点为一般平面上的多边形时，由于测点为塔板测点，所以测点一定呈二元线性关系，即为一个平面，综合分析，建立如下的回归模型：z=β0+β1x+β2y+ε

利用Matlab程序可以得到4次观测各层的回归系数，多元线性回归时，可以根据残差剔除测量粗差点，剔除后，再重新估计参数，见表3。

通过以上综合分析，拟合每一层测点数据的圆球方程为：

（x-xi）2+（y-yi）2+（z-zi）2=r2

球曲面的方程的另一种形式为：

x2+y2+z2+ax+by+cz+d=0

当第i层有个点时，所拟合的球面方程可以表示为：

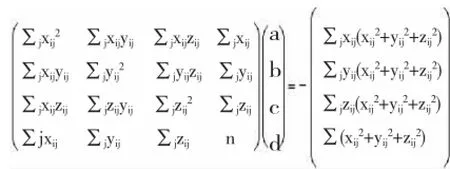
可得出：

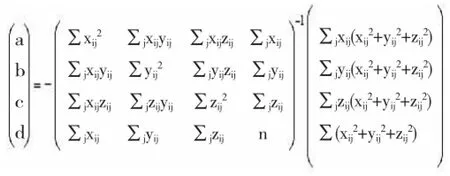
拟合得到古塔的各层拟合圆球曲面球心坐标为表4。利用向量空间数学知识知拟合圆圆心在平面上可得：

β0+β1Xi+β2Yi-z=0

同时圆心与球心连线的空间直线方程为：

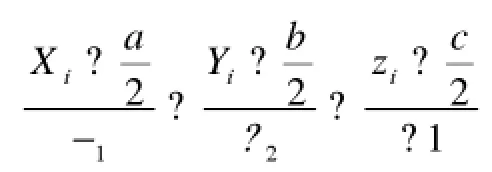
表4　

联立方程组可得：

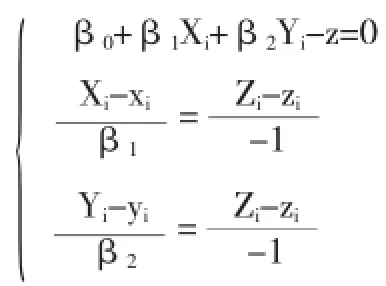
解方程可得拟合圆圆心的坐标为：

利用该模型得到4次观测古塔的各层中心坐标为表5。

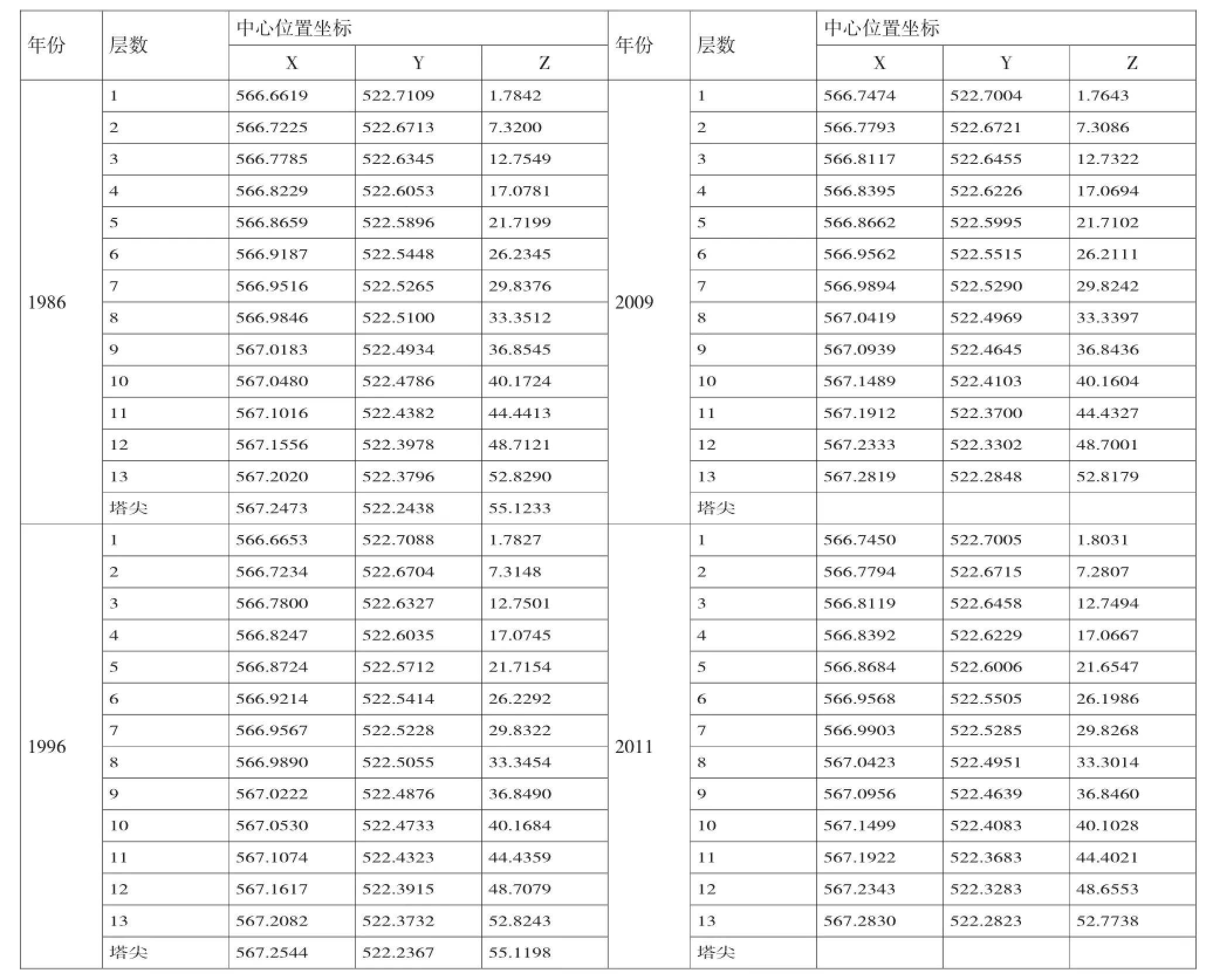
表5　

［1］岳忠玉.高等数学［M］.西安：西北大学出版社，2012.

［2］胡志晓.古塔倾斜观测和数据分析［J］.江苏建筑，6（145）：34-44，2011.

［3］马莉.MATLAB数学实验与建模［M］.北京：清华大学出版社，2010.

O175.13

A

1008-7508（2015）08-0058-03

2015－01－15

徐翠翠（1984－），女，陕西铁路工程职业技术学院基础课部数学教研室，讲师，主要从事数学模型研究。