消弱永磁驱动器齿槽转矩的斜极优化方法
2015-08-24石松宁王大志
石松宁 王大志
消弱永磁驱动器齿槽转矩的斜极优化方法
石松宁1,2王大志1
(1. 东北大学信息科学与工程学院 沈阳 110004 2. 辽宁工程技术大学电子信息工程学院 葫芦岛 125000)
采用斜极结构消弱永磁驱动器的齿槽转矩,利用解析方法推导出具有斜极结构的永磁驱动器齿槽转矩解析表达式。采用Ansys有限元仿真和中心复合实验设计获取响应值,根据响应值建立斜极结构永磁驱动器的二阶响应面回归模型。并基于该模型,选择永磁驱动器齿槽转矩最小为目标,利用粒子群优化算法对其主要结构参数进行优化,得出最优结构参数组合。对斜极结构永磁驱动器分别进行了解析和优化,结果表明,优化方法可以显著地消弱永磁驱动器的齿槽转矩,避免产生转矩波动,提高了系统的控制准确度,证明所得出的结论是正确、有效的。
永磁驱动器 斜磁极 响应面法 有限元法 粒子群算法
0 引言
永磁驱动器(Permanent Magnet Drive,PMD)是在永磁磁力耦合器的基础上发展而来的。近年来,永磁调速技术集中应用于提高设备的性能、可靠性及制造装配的准确度上。国内外对永磁驱动器电磁场性能计算的研究已经取得了一定的成果[1-4],但是永磁调速技术还存在很多有待解决的问题。例如,与永磁电机相似,永磁驱动器中永磁体与开槽导体盘相互作用产生齿槽转矩,进而产生振动,影响系统的控制准确度。所以,在永磁驱动器的设计中必须采用相应的方法消弱齿槽转矩。
本文针对具有开槽结构的永磁驱动器,提出一种斜磁极的消弱齿槽转矩的方法,推导出永磁驱动器磁极斜极的齿槽转矩解析表达式。利用Ansys有限元软件和中心复合实验设计获取(Central Composite Design,CCD)响应值,应用响应值建立斜极结构永磁驱动器二阶响应面回归模型,在此模型的基础上以齿槽转矩最小为目标,利用粒子群优化算法对斜极结构PMD进行参数优化设计,得到一组最优的参数优化结果,最后采用Ansys有限元仿真进行了验证。
1 机械结构和工作原理
永磁驱动器的机械结构如图1所示,该结构为双组盘式结构(单组只包含一个导体转子和一个永磁转子),主要由四个圆盘形钢架、两个导体环和两个嵌入永磁体的铝盘组成。其中的两个钢架分别和导体环固定在一起组成导体转子,并与电机端联接。为了优化涡流路径,避免产生杂散电流,如图2所示导体环上开有梯形槽。另外的两个钢架和磁盘固定在一起组成永磁转子,与负载端联接。永磁体如图2所示,永磁体沿圆周均匀分布且N、S极交替放置。

图1 永磁驱动器的机械结构Fig.1 Machinery structure of PMD
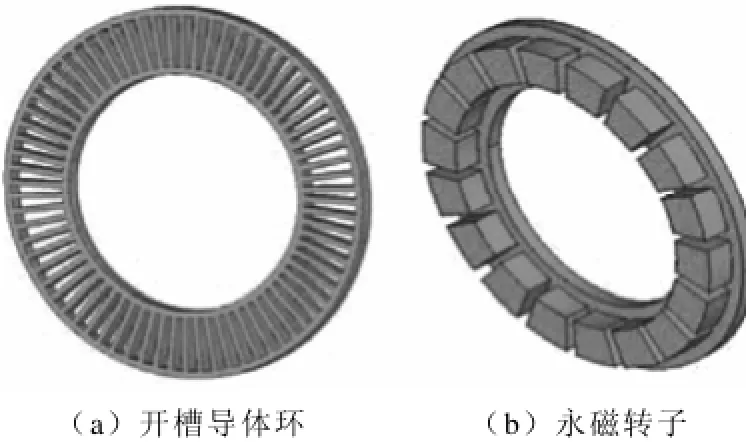
图2 开槽导体环和永磁体排列示意图Fig.2 Schematic of slotted copper disk and permanent magnet arrangement
2 永磁驱动器斜磁极时齿槽转矩的解析
2.1永磁驱动器齿槽转矩产生机理
如图2所示由于导体环上齿槽的存在,引起导体环与永磁体之间的气隙不均匀,一个齿距内的磁通相对集中于齿部,使得气隙磁导不是常数,当导体转子带动永磁转子旋转时,气隙磁场的储能发生变化,产生齿槽转矩。齿槽转矩会使永磁驱动器转矩和转速发生波动,从而影响系统的控制准确度,所以设计时应考虑避免产生过大的齿槽转矩。通常齿槽转矩的抑制方法包括减小槽口宽度、磁极偏移、斜槽和斜极等[5-9]。本文采用永磁体整体斜极的方法来消弱永磁驱动器的齿槽转矩。
2.2斜磁极时齿槽转矩的解析表达式
如图3给出了永磁驱动器永磁体斜极时的示意图,R1、R2分别代表永磁体的内半径和外半径。设N为磁极所斜的齿距数,θp=2π/z为齿距角,磁极倾斜的角度以导体环上齿距为计算单位。根据几何关系得到径向长度r处所斜的角度为[10]
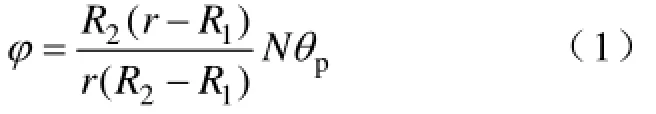

图3 磁极斜极示意图Fig.3 Schematic of magnet skewing
根据文献[10]可得永磁驱动器的齿槽转矩为


式中,L为永磁驱动器导体环厚度;R1、R2分别为永磁体的内半径和外半径;Gn和Brnz为傅里叶系数;z为导体盘开槽数。

当磁极倾斜一个齿距,即N=1时,将θp=2π/z代入上式并整理得

可见,当磁极倾斜一个齿距时,永磁驱动器齿槽转矩各谐波分量有一定的消弱。所以本文提出的斜磁极消弱齿槽转矩的方法是可行的。由式(3)可以看出影响永磁驱动器斜极结构的齿槽转矩大小的主要结构参数有导体环厚度L,导体环开槽数z,齿距数N和斜极时永磁体的内外半径差值R2-R1。
3 建立斜极结构的永磁驱动器响应面模型
为了分析的方便,本文在确保永磁体内半径R1不变的情况下,选择永磁驱动器导体环厚度L、导体环开槽数z、齿距数N和永磁体外半径R2作为设计变量,齿槽转矩作为响应变量。本文通过中心复合实验设计选取合适的实验点,利用Ansys有限元分析软件对实验点处的齿槽转矩进行计算分析,获取响应值。最后根据响应值建立斜极结构永磁驱动器响应变量与设计变量的二阶响应面回归模型。
3.1 有限元建模
本文采用Ansys有限元仿真软件建立永磁驱动器开槽结构的三维有限元模型。仿真模型如图4所示,永磁驱动器具体的三维仿真参数见表1。
图4 开槽结构永磁驱动器的三维有限元仿真模型Fig.4 3D finite-element model of the PMD
3.2 中心复合实验设计
响应面设计中最经典的方法是中心复合设计(Central Composite Design,CCD)[11]。采用CCD设计能用较少的实验次数进行全面的分析研究。本文进行了4因素3水平的中心复合设计。表2为设计变量因素水平表。

表1 PMD的三维仿真参数Tab.1 3D simulation parameters of the PMD
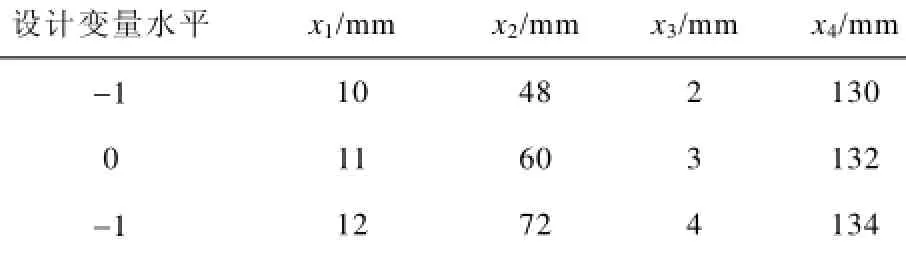
表2 设计变量因素水平表Tab.2 The level of design parameters
表2中x1、x2、x3和x4分别代表永磁驱动器导体环厚度L、导体环开槽数z、齿距数N和永磁体外半径R2。根据表2中的数据进行中心复合实验设计,实验结果示于表3。表3中各组设计实验对应的齿槽转矩响应值是通过Ansys有限元软件计算得到的。

表3 实验设计及计算结果Tab.3 The experimental design and results
3.3 响应面建模
为了更精确地表达设计变量和响应变量之间的关系,永磁驱动器的齿槽转矩用带交叉项的二阶回归方程进行描述[12,13],即

式中,k为设计变量个数;xi为设计变量;Y为响应变量;ζ为一个随机误差向量;βi为回归系数,其个数为[(k+1)(k+2)]/2,βi可由实验数据响应值利用最小二乘发估算。

式中,ˆβ是由βi组成的向量;X为因素水平矩阵;Y为响应值列向量。
根据式(6)的计算方法和表3中的数据,应用Matlab软件编程可计算得到二阶回归方程系数向量ˆβ,由此得到齿槽转矩的二阶回归方程为
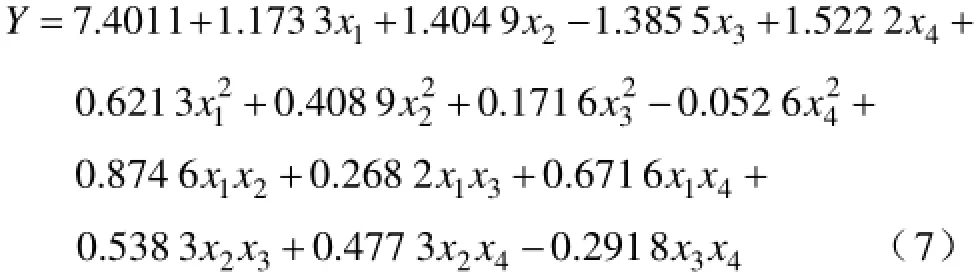
4 基于齿槽转矩最小的参数优化设计
通过响应面法得到齿槽转矩的二阶回归模型后,以齿槽转矩最小为优化目标,选取影响齿槽转矩的四个主要结构参数为优化变量,建立基于粒子群算法的永磁驱动器斜极结构优化设计模型。
斜极结构永磁驱动器参数优化的目标是齿槽转矩最小,优化目标函数可以表示为
minY=obj (z,L,N,R2) (8)式中,Y代表齿槽转矩的二阶回归方程。
显然该优化模型是一个非线性、多参数的复杂系统,难以采用常规优化算法。所以本文采用粒子群优化算法对斜极结构PMD进行参数优化设计。
在粒子群算法中,粒子群由n个粒子构成,其中第i个粒子代表一个D维位置矢量xi=(xi1,xi2,…,xid)和D维速度矢量vi=(vi1,vi2,…,vid)。每个粒子的位置矢量xi代表最优问题的一个解。将xi代入目标函数可以求出对应的适应值,根据适应值的大小衡量xi是否为所要求的最优解。每个粒子根据适应值搜索到最优解和所有粒子的全局最优解参考图5优化流程,粒子群算法(Particle Swarm Optimization,PSO)目标函数的适应值实时计算由齿槽转矩的二阶回归方程完成,粒子群按照式(9)和式(10)的速度-位置模型进行寻优操作[14,15]。


图5 PSO优化流程Fig.5 The flowchart of PSO optimization
优化目标函数如式(8),在满足PMD输出转矩不小于额定转矩的情况下,确定优化参数的约束范围为
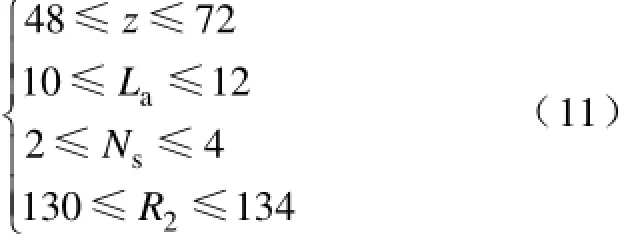
采用粒子群算法进行搜索,得到的一组优化结果见表4。
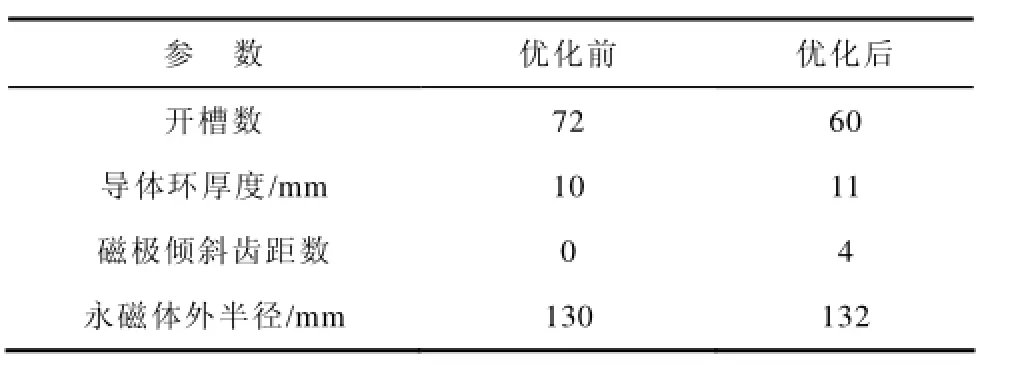
表4 优化前后PMD结构参数Tab.4 The structural parameters of non-optimized and optimized PMD
5 优化结果验证
为了验证基于斜极优化的永磁驱动器齿槽转矩消弱方法的有效性,采用有限元进行仿真计算,不斜极时永磁驱动器结构参数见表1,优化后斜极结构永磁驱动器结构参数见表4。
图6为根据有限元计算结果画出的永磁驱动器不斜极结构、斜极结构解析结果和优化后的齿槽转矩波形图,由波形比较可以看出,永磁驱动器不斜极结构齿槽转矩较大,齿槽转矩幅值为20N·m。斜极结构解析结果使得永磁驱动器齿槽转矩进一步减小,优化后的斜极结构可以大幅度消弱PMD的齿槽转矩,优化后齿槽转矩幅值为4.8N·m,比不斜极结构减小了79%。证明了本文提出的斜极结构优化方法是有效的。

图6 磁极斜极齿槽转矩仿真曲线Fig.6 Simulation curres of cogging torque with magnet skewing (3D FEM)
6 结论
本文采用磁极斜极法所得的齿槽转矩解析表达式,利用Ansys有限元仿真和中心复合实验设计获取齿槽转矩的响应值,根据响应值建立斜极结构永磁驱动器二阶响应面回归方程,采用粒子群优化算法对影响齿槽转矩的主要参数进行优化,寻找使齿槽转矩最小的最优组合。利用有限元仿真软件分别计算出不斜极结构和斜极结构解析及优化后的齿槽转矩,有限元分析结果表明优化后的斜极结构可以显著消弱永磁驱动器的齿槽转矩。
[1] Wallace A, Von Jouanne A, Jeffryes R. Comparison testing of an adjustable-speed permanent-magnet eddycurrent coupling[C]. IEEE Proceedings of Pulp and Paper Industry Technical Conference, Atlanta, 2000: 73-78.
[2] Wallace A, Von Jouanne A. Industrial speed control: are PM couplings an alternative to VFDs?[J]. IEEE Industry Applications Magazine, 2001, 7(5): 57-63.
[3] Wallace A, Von Jouanne A, Williamson S, et al. Performance prediction and test of adjustable, permanentmagnet, load transmission systems[C]. Proceedings of IEEE Industry Applications Society 36th Annual Meeting, 2001: 1648-1655.
[4] Salon S J, Yukenmez Ergene L, Wendling P F. 3D transient magnetic modeling of braking torque in a rotating conducting disc[C]. Proceedings of International Electric Machines and Drives Conference-IEMDC, Cambridge, 2001: 188-191.
[5] Abbaszadeh K, Rezaee Alam F, Saied S A. Cogging torque optimization in surface-mounted permanent magnet motors by using design of experiment[J]. Energy Conversion and Management, 2011, 52(10): 3075-3082.
[6] 杨玉波, 王秀和, 朱常青. 基于分块永磁磁极的永磁电机齿槽转矩消弱方法[J]. 电工技术学报, 2012, 27(3): 74-76. Yang Yubo, Wang Xiuhe, Zhu Changqing. Effect of permanent magnet segmentation on the cogging torque of surface mounted permanent magnet motors[J]. Transactions of China Electrotechnical Society, 2012, 27(3): 74-76.
[7] Hwang K Y, Lin Hai, Rhyu S H, et al. A study on the novel coefficient modeling for a skewed permanent magnet and overhang structure for optimal design of brushless DC motor[J]. IEEE Transactions on Magnetics, 2012, 48(5): 1918-1923.
[8] 杨玉波, 王秀和, 丁婷婷. 基于单一磁极宽度变化的内置式永磁同步电动机齿槽转矩消弱方法[J]. 电工技术学报, 2009, 24(7): 42-44. Yang Yubo, Wang Xiuhe, Ding Tingting. Different pole-arc width combination for reducing cogging torque of interior-magnet PMSM[J]. Transactions of China Electrotechnical Society, 2009, 24(7): 42-44.
[9] 刘婷, 欧阳红林, 黄守道, 等. 基于重复单元消弱永磁电机齿槽转矩方法[J]. 电工技术学报, 2011, 26(12): 43-48.Liu Ting, Ouyang Honglin, Huang Shoudao, et al. Reducing cogging torque in permanent magnet wind power generators based on repeat unit[J]. Transactions of China Electrotechnical Society, 2011, 26(12): 43-48.
[10] 周俊杰, 范承志, 叶云岳, 等. 基于斜磁极的盘式永磁电机齿槽转矩消弱方法[J]. 浙江大学学报, 2010, 44(8): 1549-1550. Zhou Junjie, Fan Chengzhi, Ye Yunyue, et al. Method for reducing cogging torque based on magnet skewing in disc-type permanent magnet motors[J]. Journal of Zhejiang University, 2010, 44(8): 1549-1550.
[11] 张志红, 何桢, 郭伟. 在响应曲面方法中的三类中心复合设计的比较研究[J]. 沈阳航空工业学院学报, 2007, 24(1): 87-91. Zhang Zhihong, He Zhen, Guo Wei. A comparative study of three central composite designs in response surface methodology[J]. Journal of Shenyang Institute of Aeronautical Engineering, 2007, 24(1): 87-91.
[12] 石松宁, 王大志, 时统宇. 基于RSM的永磁驱动器偏心磁极的多目标优化[J]. 仪器仪表学报, 2014, 35(9): 1966-1967. Shi Songning, Wang Dazhi, Shi Tongyu. Multiobjective optimization of eccentric magnet pole for permanent magnet drive based on response surface methodology[J]. Chinese Journal of Scientific Instrument, 2014, 35(9): 1966-1967.
[13] Vafaeesefat A. Optimization of composite pressure vessels with metal liner by adaptive response surface method[J]. Journal of Mechanical Science and Technology, 2011, 25(11): 2811-2816.
[14] Liu W, Liu L, Chung I, et al. Real-time particle swarm optimization based parameter identification applied to permanent magnet synchronous machine[J]. Applied Soft Computing, 2011, 11(2): 2556-2564.
[15] Modares H, Alfi A, Fateh M. Parameter identification of chaotic dynamic systems through an improved particle swarm optimization[J]. Expert Systems with Applications, 2010, 37(5): 3714-3720.
石松宁 女,1982年生,博士研究生,讲师,研究方向为永磁驱动器的建模和优化设计。
王大志 男,1963年生,教授,博士生导师,研究方向为电力系统与电力传动。
Magnet Skewing Optimization Method for Reducing Cogging Torque in Permanent Magnet Drive
Shi Songning1,2Wang Dazhi1
(1. Northeastern University Shenyang 110004 China 2. Liaoning Technical University Huludao 125000 China)
In this paper, the magnet skewing structure is adopted to reduce the cogging torque in permanent magnet drive. The analytical method is used to give the expression of the cogging torque. The quadratic polynomials are employed to construct response surface model based on the response obtained by the Ansys software and the central composite design (CCD) experiment method. Based on this model, the minimal cogging torque is taken as the optimal objective, and then the particle swarm optimization (PSO) algorithm is used to perform optimization and obtain the optimal structure parameters of the PMD. At last, the permanent magnet drive with magnet skewing structure is analyzed and optimized with above method. The results verify that the cogging torque can be notably reduced with this optimization method.
Permanent magnet drive, magnet skewing, response surface methodology, finite element method, particle swarm algorithm
TP215
辽宁省技术创新重大项目资助(201309001)。
2013-12-04 改稿日期 2014-10-20
