基于改进磁场分割法的开关磁阻电机 径向力波抑制能力解析计算
2015-08-24王秀和杨玉波
张 鑫 王秀和 杨玉波
基于改进磁场分割法的开关磁阻电机 径向力波抑制能力解析计算
张鑫王秀和杨玉波
(山东大学电气工程学院 济南 250061)
电磁振动的抑制是开关磁阻电机研究的热点问题之一。因此提出了一种基于抛物线弧改进的磁场分割法,用于复杂定子、转子形状的开关磁阻电机气隙磁导计算。基于改进磁场分割法,提出了一种开关磁阻电机径向力波抑制百分比的解析计算方法,通过转子形状改变带来的气隙磁导的变化,以比值方式计算了径向力波的抑制程度,可以为基于改变定子、转子形状的振动抑制设计提供依据。以转子两侧开槽的开关磁阻电机为例,分别使用基于抛物线弧和椭圆弧的磁场分割法计算了绕组电感和径向力波抑制百分比,并与有限元分析和样机试验结果进行对比验证,结果表明改进的磁场分割法和径向力波抑制百分比计算方法是正确、有效的。
开关磁阻电机 磁场分割 气隙磁导 转子开槽 振动抑制
0 引言
近年来,开关磁阻电机(Switched Reluctance Motor,SRM)在工业中的很多领域,如锻压机械、纺织机械和混合动力汽车中得到了广泛应用。它具有结构简单可靠、功率密度高、动态响应快和控制灵活等优点。其定子上安放集中式绕组,转子上无绕组,具有较高的可靠性和鲁棒性,但由于双凸极结构的影响,开关磁阻电机具有较大的转矩脉动、电磁振动和噪声,限制了其进一步推广[1-3]。
有限元法和等效磁路法是电机静态特性计算的主要方法[4-7]。有限元法计算准确度较高,但模型建立耗时长,设计调整不方便。等效磁路法计算速度快,参数调整简单,但由于双凸极结构存在显著的边缘效应,电机的非线性和定子、转子齿间局部饱和严重,其计算准确度比有限元法低。为提高等效磁路法的计算准确度,提出了变结构等效磁路法[8]、三维等效磁路法[9,10]和非线性等效磁路[11]等改进的计算方法。等效磁路法仍是电机设计初期快速计算的主要手段。气隙磁导的计算是等效磁路法准确与否的关键。通常采用磁场分割法计算气隙磁导[12,13]。磁场分割法是根据气隙磁场的分布规律,利用某些与磁力线接近的直线、圆弧等把气隙磁场分割为若干具有规则形状的磁通管区域,通过串、并联关系求得整个区域的总磁导。但是在面对某些复杂形状转子(如转子齿侧面开槽)的时候,圆弧或椭圆弧这种曲线形状的磁通管往往准确度较差或计算复杂。本文提出一种用与磁力线形状相似的抛物线弧曲线方程计算气隙磁导,计算简便灵活,适用于各种定转子齿型。
开关磁阻电机振动、噪声和转动脉动的抑制一直是研究的热门领域,也是亟待解决的重要问题。开关磁阻电机的电磁噪声和振动主要是由定子的径向振动引起。本文作者在文献[14]中提出一种在转子齿两侧开槽的方法,改变转子表面磁通密度方向,减小开关磁阻电机气隙中的径向磁通密度,从而削弱径向力波,达到抑制电机振动的目的。但文中是通过大量的有限元分析确定转子开槽的尺寸,每当调整尺寸时都要重新建模和剖分,占用时间较长,过程繁琐。
本文基于改进的磁场分割法计算气隙比磁导,提出了复杂定子、转子形状开关磁阻电机径向力波抑制百分比的解析计算方法,不具体计算电机的径向力波值,通过计算电机结构尺寸改变前后的径向力波抑制程度,来表示电机振动抑制能力的变化。使用改进的磁场分割法,计算气隙各个区域的磁导,并推导转子表面各个区域磁通密度的径向分量和切向分量,通过麦克斯韦张量法推导定子、转子外形更改前后径向力波的表达式,以比值的方式描述径向力波的抑制程度。一些非线性的中间变量通过比值可以消去,计算简单,也减少了影响计算误差的因素。以转子两侧开槽的开关磁阻电机为例进行验证,计算结果与有限元分析和试验结果较为吻合,同时也与基于椭圆弧的磁路计算结果相比较,效果较好,验证了抛物线弧型磁通管计算气隙磁导的有效性和准确性。
1 基于抛物线弧的气隙磁导的计算
1.1改进的磁场分割法
磁场分割法通常利用与磁力线形状相似的曲线来模拟磁力线在气隙中的路径,并且把气隙空间按照曲线类型划分成若干区域以便于计算[15,16]。如 图1所示,磁力线与抛物线弧和椭圆弧几乎重合,形状十分相似,抛物线弧和椭圆弧明显比圆弧更接近磁力线在气隙中的路径形状。

图1 气隙中的磁场分布Fig.1 The magnetic distribution of air-gap
采用椭圆弧计算磁路长度需要确定焦点位置和长短轴的长度,如果遇到转子侧面开槽等复杂定子、转子外形时,计算非常繁琐。而抛物线方程只有一个特征系数,只要确定抛物线原点位置和线上一点坐标就可以很方便地计算抛物线的弧长。
使用磁场分割法推导气隙磁通密度、径向力波抑制百分比及气隙磁导公式时有如下假设:①铁心磁导率μFe=∞;②磁场沿轴向均匀分布;③忽略饱和的影响,忽略漏磁通。
1.2普通转子开关磁阻电机气隙磁导计算
应用磁场分割法中磁通管的概念可以推导出气隙比磁导的计算公式,比磁导是气隙中各磁通路径的磁导分量[12,13],气隙磁导Λ 等于轴向有效长度lFe、空气磁导率μ0和比磁导λ 三者的乘积

式中,l为气隙磁通路径长度;S为磁路面积;dx为定子极弧的单位长度。
应用抛物线弧长公式的比磁导λ为

随着定子和转子相对位置的变化,气隙磁场区域的划分和磁导的计算有所不同,定子和转子齿轴线之间的夹角α 在转子半个极距内,可以分为三个特征区间,满足

式中,τr是转子极距;α1=(βr-βs)/2,α2=(βr+βs)/2, βs和βr分别为定子和转子的齿宽度。
以特征区间Ⅱ为例(区间Ⅰ和区间Ⅲ的计算参见附录),当定子、转子相对位置如图2所示时,气隙比磁导λ 按照P1~P4四个区域分为四部分

图2 普通转子开关磁阻电机气隙磁场的区域分割Fig.2 The magnetic divisions on air-gap of normal rotor
设P1区域的磁力线曲线方程为L1:y2=2q1x,线上一点的坐标为U(rgh+,sbβ-),其中,g是气隙长度;hr是转子齿高;b是定子、转子齿重合长度。那么抛物线系数

P1区域的比磁导为

P2区域的比磁导为

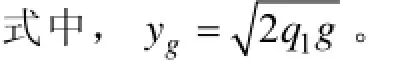
P3区域的比磁导为

在大量的有限元计算中发现:P4区域在定子、转子的各个相对位置时的磁路变化不大,不妨设置固定的磁导计算区域。设P4区域的磁力线曲线方程 为L4:y2=2q4x,线上一点的坐标为其中,hs是定子齿高,那么
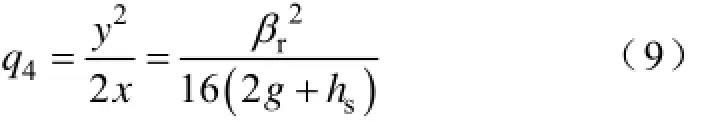
P4区域的比磁导为

1.3转子齿两侧开槽开关磁阻电机气隙磁导计算
本文作者在文献[14]中提出一种通过转子齿两侧开槽抑制电机径向力波的方法,转子齿的结构如图3所示,本文将以5.5 kW、1000 r/min的12/8极开关磁阻电机为例进行振动抑制能力的解析计算。
解析计算的基础是气隙磁导的计算。以特征区间Ⅱ为例,当定子、转子相对位置如图3所示时,气隙比磁导λ′按照P1~P5五个区域分为式(11)所示的五部分

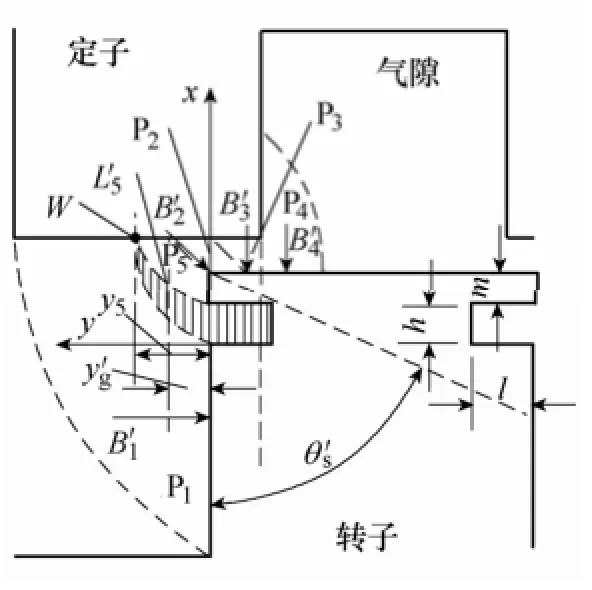
图3 双开槽转子开关磁阻电机气隙磁场的区域分割Fig.3 The magnetic divisions on air-gap of slotted rotor
开槽转子P1区域的磁力线曲线方程与普通转子相同,但是磁导计算时的积分上限不同,为

P3和P4区域的磁导与普通转子相同区域磁导相同,即

设P5区域的磁力线曲线方程为5L′:252yq x′=,线上一点的坐标为W(gm+,5y),则 P5区域的比磁导为
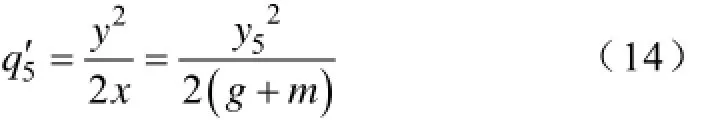


P2区域的比磁导为


其他区间的比磁导也可以用以上方法进行推导和计算,本文不再赘述。气隙磁导的计算是等效磁路法结果准确与否的关键,也是本文径向力波抑制百分比计算的关键。实际计算中可把定子、转子相对位置三个大区间各自再划分成若干个小区间[17],可以使结果更加准确。
2 开关磁阻电机径向力波抑制百分比的计算
2.1普通转子开关磁阻电机气隙磁通密度计算
气隙磁通密度的计算过程随着定子、转子相对位置的改变而有所区别,如图2所示的定子、转子相对位置为例,气隙分为四个区域计算磁通密度,其中P1区域普通转子表面的磁通密度为B1,垂直于铁心表面,相对于转子属于切向磁通密度。
P2区域(斜阴影)中,转子顶部表面磁通密度为B2,满足

式中,Bn2和Bt2分别为P2区域径向和切向磁通密度分量;θr可以近似为转子齿对角线与侧边的夹角。
P3区域(竖阴影)和P4区域转子齿顶表面的磁通密度B3和B4可以认为都是转子的径向磁通密度。
2.2开槽转子开关磁阻电机的气隙磁通密度计算
定子、转子相对位置如图3所示时,侧面开槽转子的气隙可以分割为五部分。P1区域齿侧面开槽转子表面的磁通密度为B1′,垂直于转子侧表面,相对于转子属于切向磁通密度。
开槽转子与普通转子气隙磁场分割的不同在于P1和P2区域中间多分了一个P5区域,以及多了一个无磁力线区域(见图3阴影部分),侧面的槽增大了气隙长度,使得本来应该从开槽位置进入铁心的磁通路径,改为从齿顶进入,因此改变了齿顶局部表面的磁通密度方向。
P5区域中转子表面磁通密度为B5′,其垂直于转子齿顶侧表面,相对于转子属于切向磁通密度。
P2区域转子顶部表面磁通密度为B2′,Bn′2和Bt′2分别是P2区域径向和切向磁通密度分量,满足

P3和P4区域转子齿顶表面的磁通密度3B′和4B′都是径向磁通密度,且与普通转子相同区域的磁通密度相等,即

2.3径向力波抑制百分比的计算
双凸极电机严重的非线性和局部饱和,以及电流、电感和磁链等变量解析计算误差的影响,会造成径向力波的解析计算值失真。为了减小饱和以及这些变量带来的误差,避免计算径向力波的具体值,定义了径向力波抑制百分比δ 来表示转子齿两侧开槽对径向力波的削弱程度,即

式中,np为正常电机径向力波;np′为转子齿两侧开槽后电机的径向力波。
根据麦克斯韦张量法[18],电机转子表面的径向力波为

式中,pt为切向力波;Bn为径向磁通密度;Bt为切向磁通密度。
将转子作为一个整体,由式(17)~式(21)可得
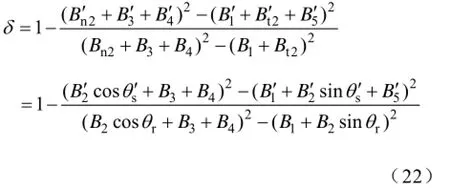
气隙磁通密度B为

式中,F是磁动势;S为主磁通穿过的面积。
由式(1)、式(22)和式(23)可得
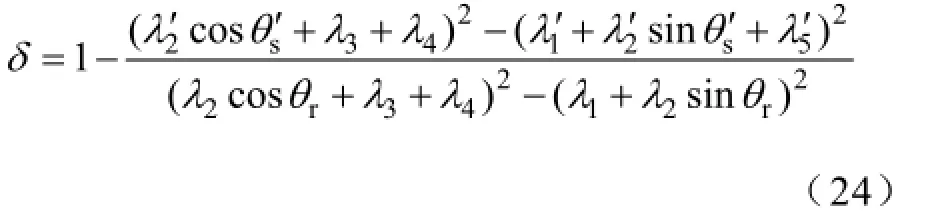
由式(24)可知,气隙磁通密度、磁动势等变量在推导过程中都消去了,只需计算气隙各个区域的比磁导,就可以获得不同开槽尺寸下的随定子、转子相对位置变化的径向力波抑制百分比曲线,从而可以得到在合理范围内的具有最大径向力波抑制能力的开槽尺寸,为电机的减振设计提供参考。本文提出的方法,没有计算具体的径向力波数值,所以避免了繁琐的磁链、电感等变量的计算,计算过程相对简单。由式(24)可以看出,理想状态下开关磁阻电机定子和转子外形尺寸的改变,对于电机自身振动抑制能力的影响,根本上是改变了气隙磁场的分布,表现为气隙比磁导发生了变化,而与电感、电流等变量没有关系。
3 有限元和样机验证
3.1样机参数
本文以5.5 kW的12/8极开关磁阻电机为例,研究转子开槽对电机振动抑制能力的影响。样机的主要参数见下表,样机试验环境和开槽转子如图4所示。

表 样机的主要参数Tab. Parameters of the SRM prototype motor

图4 样机试验环境和开槽转子Fig.4 The prototype motor and sloted rotor
3.2电感的计算与验证
电感特性是相电感随转子位置和电流变化的规律,是开关磁阻电机的重要技术参数,很多文献研究了开关磁阻电机电感的解析计算[19-22]。开关磁阻电机非导通相无电流,所以相间互感很小,相电感可以用绕组自感表示。忽略铁心饱和时,绕组自感Lj可以表示为式中,N、Λ∑和R∑分别为绕组匝数、磁路总磁导和磁阻。

本文使用抛物线弧磁路和椭圆弧磁路获得的气隙磁导进行电感计算,除了磁场分割和磁导的计算不同,其他条件相同。样机的实测电感和磁路法计算电感曲线如图5所示。
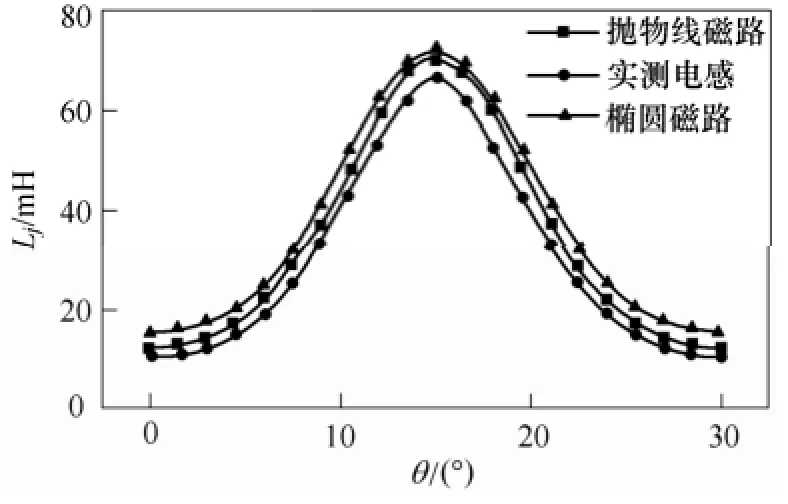
图5 样机的相电感Fig.5 The phase inductance of prototype motor
可以看出,解析计算电感比样机实测电感整体偏大,在最大电感处两种磁路算法的结果相近。抛物线磁路法的平均误差为12.9%,椭圆磁路法的平均误差为21%,前者更接近实测值。
3.3径向力波抑制百分比
开槽转子与普通转子的径向力波抑制百分比如图6所示,其中α 是定子和转子齿极中心线夹角。可以看出,α 越大开槽对振动抑制的效果越好。磁路计算结果与有限元分析的结果相近,由于没有考虑饱和等因素的影响,磁路法获得的结果比有限元法整体偏大。α 很小的时候基于抛物线弧与基于椭圆弧的磁路计算结果比较相似,这是因为定子、转子中心线对齐时,磁通主要从齿顶流过,转子开槽对气隙磁场影响最小,随着α 的增大,椭圆弧磁路计算结果误差略大一些,抛物线弧的磁路计算结果更接近有限元分析。

图6 径向力波抑制百分比Fig.6 The weakened percentage of radial force wave
3.4样机振动测试
制作了两台开关磁阻电动机样机进行振动的对比试验。样机A的转子齿两侧开槽,样机B为普通转子。开槽转子的开槽深度为2.5mm,开槽宽度为4mm,齿顶高度为3mm。
样机绕组电流通过控制器中的电流传感器和采样电阻采集。转速为1 000r/min、额定负载时样机A与样机B相电流波形如图7所示,采样电阻的电压峰值均为3.72V,换算后斩波限流值均为22.5A,开槽后电机的负载能力基本没有变化。
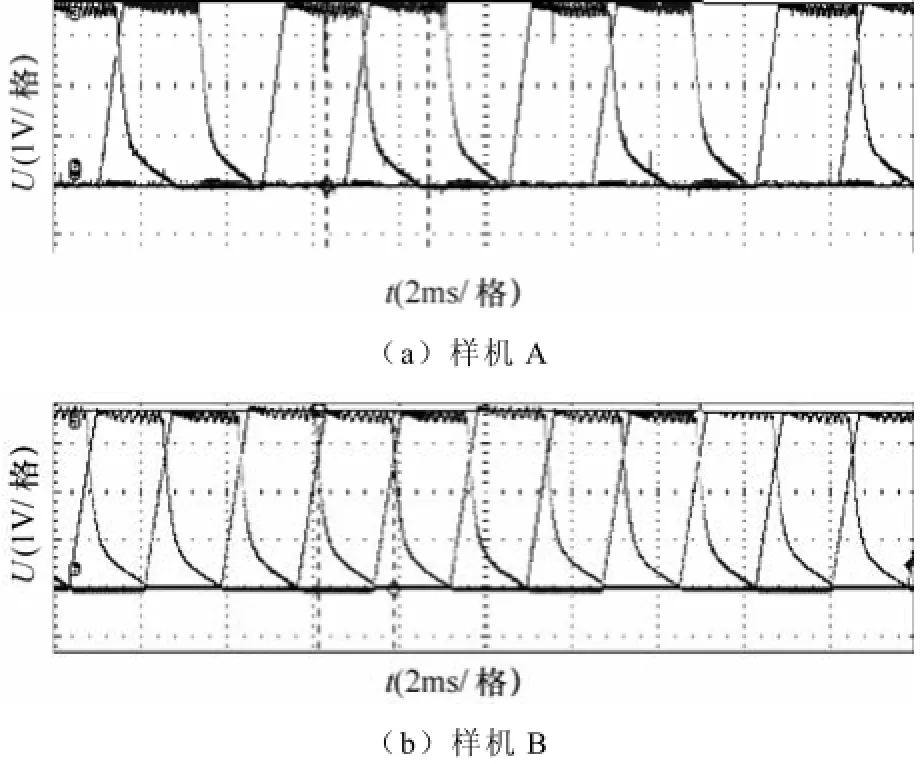
图7 样机绕组电流采样波形Fig.7 The current sampling waveforms of prototype motors
使用IEPE型压电加速度传感器进行样机振动数据的采集,传感器安装于机座外表面,位置正对着定子齿。振动测试的结果如图8所示,开槽转子电机的振动得到了一定的抑制。

图8 样机振动加速度Fig.8 Acceleration of vibration waveforms on prototypes motors
由于振动加速度与径向力波成正比关系,将图8中的数据代入式(26)计算振动抑制百分比。
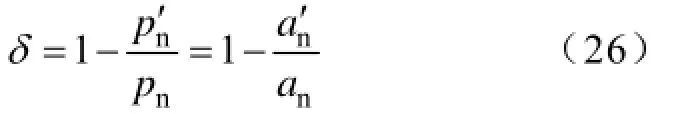
式中,na和na′分别是普通转子电机和开槽转子电机的径向振动加速度,结果如图9所示。可以看出,在大部分区域里(δ>0的区域),开槽电机的振动都得到了抑制。样机的相实际导通区间为9°≤α≤ 14°,假设绕组关断时电流为零,三相绕组按顺序导通,由图6可知磁路计算的径向力波抑制百分比δ 的平均值为8.43%。图9中样机试验测得的径向力波抑制百分比δ 的平均值为6.69%,二者比较接近,说明本文提出的计算方法是有效、准确的。

图9 样机径向力波抑制百分比Fig.9 The weakened percentage of radial force wave on prototype motors
4 结论
本文提出了一种基于抛物线弧磁通管改进的磁场分割法计算气隙磁导,比传统的使用圆弧或椭圆弧的方法计算过程更简单。以开关磁阻电机为例,提出了转子两侧开槽的振动抑制百分比的解析计算方法,经过了有限元法和样机试验验证,并得到以下结论:
(1)改进的磁路分割法适合计算复杂定子、转子齿形的气隙结构,比传统的椭圆弧形磁通管的计算准确度略高(忽略磁饱和)。
(2)本文使用麦克斯韦张量法的表面力波方程并没有计算具体的转子表面径向力波数值,而是计算径向力的波削弱程度,这个过程中不需要考虑电流、电感、磁链等非线性很强、很难采集的变量,只需要计算气隙形状改变带来的气隙磁导的变化。对于其他类型双凸极电机或通过改变定子、转子齿形进行振动抑制的设计,都可以采用这个思路进行磁路验算,可以大大提高优化设计的效率,有较强的通用性。
附 录
普通转子开关磁阻电机在式(3)区间Ⅰ中的气隙比磁导λ 按照P1~P4区域分为四部分,即

设P1区域的磁力线曲线方程为,线上

附图1 普通转子气隙磁场的分割App. Fig.1 The magnetic divisions in air-gap of normal rotor
一点的坐标为U(sbβ+,rgh+),那么抛物线系数为

P1区域的比磁导为

在转子齿侧边有长度c区域不在P1内(以本文模型为例:srhβ<),令c所在的竖阴影区域为P2,不妨设P2内的磁力线为直线,则比磁导为
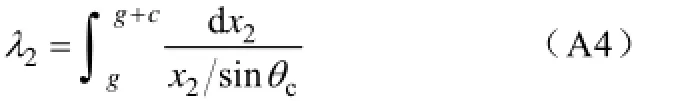
设P4区域的磁力线曲线方程为244:Ly=2q4x4,线上一点的坐标为V(r/4bβ+,s/2gh+),那么

P4区域的比磁导为

在定子齿侧边有长度a区域不在P4内,令长度a所在的斜阴影区域为P3,不妨设P3内的磁力线为直线,则比磁导为

转子齿两侧开槽的开关磁阻电机在区间Ⅰ中的气隙比磁导λ′按照P1~P5区域分为五部分
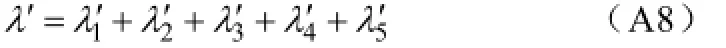
如附图2所示,开槽转子P1区域的磁力线曲线方程 为,线上一点的坐标为Z(g+hr, βs+b),

附图2 开槽转子气隙磁场的区域分割App. Fig.2 The magnetic divisions in air-gap of slotted rotor
那么抛物线系数为

P1区域的比磁导为

设P5区域磁力线曲线方程为,线上一点的坐标为W(5Y,gm+),则


P5区域的比磁导为

以本模型为例,随着定子和转子齿轴线之间的夹角α 的减小,P2区域内的c长度随之减小至0,在这个区间内

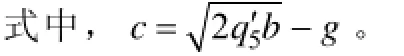
当c减至0后,2λ′按式(16)计算。
P3和P4区域的比磁导与普通转子相同,即

普通转子和开槽转子开关磁阻电机在式(3)区间Ⅲ中的气隙比磁导相同,如附图3所示,按照P1~P3区域分为三部分,即

设P1区域的磁力线曲线方程为211:Ly=2q1x1,线上一点的坐标为那么抛物线系数为

附图3 区间Ⅲ转子气隙磁场的分割App. Fig.3 The magnetic divisions in air-gap of slotted rotor in interval Ⅲ

P1区域的比磁导为

P2区域的比磁导为

设P3区域的磁力线曲线方程为线上一点的坐标为那么抛物线系数为

P3区域的比磁导为

[1] Lecointe J P, Romary R. Analysis and active redu- ction of vibration and acoustic noise in the switched reluctance motor[J]. Electric Power Applications, 2004, 151(6): 725-733.
[2] Zhu Z Q. Analytical model for predicting maximum reduction levels of vibration and noise in switched reluctance machine by active vibration cancellation[J]. IEEE Transactions on Energy Conversion, 2011, 26(1): 36-45.
[3] Chai J Y, Lin Y W, Liaw C M. Comparative study ofswitching controls in vibration and acoustic noise reductions for switched reluctance motor[J]. Electric Power Applications, 2006, 153(3): 348-360.
[4] Omekanda A M, Broche C, Renglet M. Calculation of the electromagnetic parameters of a switched reluctance motor using an improved FEM-BIEM- application to different models for the torque calcu- lation[J]. IEEE Transactions on Industry Applications, 1997, 33(4): 914-918.
[5] 孙玉坤, 吴建兵, 项倩雯. 基于有限元法的磁悬浮开关磁阻电机数学模型[J]. 中国电机工程学报, 2007, 27(12): 33-40. Sun Yukun, Wu Jianbing, Xiang Qianwen. The mathematic model of bearingless switched reluctance motor based on the finite-element analysis[J]. Pro- ceedings of the CSEE, 2007, 27(12): 33-40.
[6] Radimov N, Benhail N, Rabinovici R. Simple model of switched-reluctance machine based only on aligned and unaligned position data[J]. IEEE Transactions on Magnetics, 2004, 40(3): 1562-1572.
[7] Preston M, Lyons J P. A switched reluctance motor model with mutual coupling and multi-phase excit- ation[J]. IEEE Transactions on Magnetics, 1991, 27(6): 5423-5425.
[8] Lee C, Krishnan R, Lobo N S. Novel two-phase switched reluctance machine using commonpole E-core structure: concept, analysis, and experimental verification[J]. IEEE Transactions on Industry App- lications, 2009, 40(2): 703-711.
[9] Chun Y D, Wakao S, Kim T H. Multi-objective design optimization of brushless permanent magnet motor using 3D equivalent magnetic circuit network method[J]. IEEE Transactions on Applied Supercon- ductivity, 2004, 14(2): 1910-1913.
[10] Kim Y H, Jin C S, Kim S, et al. Analysis of hybrid stepping motor using 3D equivalent magnetic circuit network method based on trapezoidal element[J]. IEEE Transactions on Journal of Applied Physics, 2002, 91(10): 8311-8313.
[11] Moallem M, Dawson G E. An improved magnetic equivalent circuit method for predicting the characte- ristics of highly saturated electromagnetic devices[J]. IEEE Transactions on Magnetics, 1998, 34(5): 3632- 3635.
[12] 詹琼华. 开关磁阻电动机[M]. 武汉: 华中理工大学出版社, 1992.
[13] 吴建华. 开关磁阻电机的设计与应用[M]. 北京: 机械工业出版社, 2000.
[14] 张鑫, 王秀和, 杨玉波, 等. 基于转子齿两侧开槽的开关磁阻电机振动抑制方法研究[J]. 中国电机工程学报, 2015, 35(6): 1508-1515. Zhang Xin, Wang Xiuhe, Yang Yubo, et al. Vibration reduction of a switched reluctance motor using new rotor tooth with sot on each side[J]. Proceedings of the CSEE, 2015, 35(6): 1508-1515.
[15] 邓智泉, 杨钢, 张媛, 等. 一种新型的无轴承开关磁阻电机数学模型[J]. 中国电机工程学报, 2005, 25(9): 139-146. Deng Zhiquan, Yang Gang, Zhang Yuan, et al. An innovative mathematical model for a bearingless switched reluctance motor[J]. Proceedings of the CSEE, 2005, 25(9): 139-146.
[16] 丁文, 梁得亮. 12/8极双通道开关磁阻电机非线性数学模型与有限元分析[J]. 电机与控制学报, 2009, 3(2): 190-196. Ding Wen, Liang Deliang. Nonlinear mathematic model and finite element analysis for a 12/8 pole dual-channel switched reluctance machine[J]. The Electric Machines and Control, 2009, 3(2): 190-196.
[17] 王蕾, 李光友, 张强. 磁通反向电机的变网络等效磁路模型[J]. 电工技术学报, 2008, 23(8): 18-23. Wang Lei, Li Guangyou, Zhang Qiang. Network- varying equivalent magnetic circuit modeling of a flux-reversal machine[J]. Transactions of China Electrotechnical Society, 2008, 23(8): 18-23.
[18] Salon S J. Finite element analysis of electrical machines[M]. New York: Springer, 1995.
[19] 陈坤华, 孙玉坤, 吴建兵. 基于电感模型的开关磁阻电机无位置传感技术[J]. 电工技术学报, 2006, 21(11): 71-75. Chen Kunhua, Sun Yukun, Wu Jianbing. Inductance model-based sensorless control of the switched reluctance motors[J]. Transactions of China Electrotechnical Society, 2006, 21(11): 71-75.
[20] 蔡骏, 邓智泉. 一种具有容错功能的开关磁阻电机无位置传感器控制方法[J]. 中国电机工程学报, 2012, 32(36): 109-116. Cai Jun, Deng Zhiquan. A fault-tolerant sensorlesscontrol method for switched reluctance motor drives[J]. Proceedings of the CSEE, 2012, 32(36): 109-116.
[21] 程明, 周鹗, 黄秀留. 双凸极变速永磁电机的变结构等效磁路模型[J]. 中国电机工程学报, 2001, 21(5): 23-28. Cheng Ming, Zhou E, Huang Xiuliu. Variable structure equivalent magnetic circuit modeling for doubly salient permanent magnet machine[J]. Pro- ceedings of the CSEE, 2001, 21(5): 23-28.
[22] 王世山, 刘泽远, 邓智泉, 等. 无轴承开关磁阻电机动、静态电感耦合的数学拟合[J]. 电工技术学报, 2007, 22(12): 22-28. Wang Shishan, Liu Zeyuan, Deng Zhiquan, et al. Mathematical fitting of coupling dynamic and static inductance for a bearingless switched reluctance motor[J]. Transactions of China Electrotechnical Society, 2007, 22(12): 22-28.
张 鑫 男,1981年生,博士研究生,研究方向为开关磁阻电机。
王秀和 男,1967年生,教授,博士生导师,研究方向为特种电机。
The Computation of Vibration Reduction Capacity for Switched Reluctance Motor Based on Improved Magnetic Field Partition Method
Zhang Xin Wang Xiuhe Yang Yubo
(Shandong University Jinan 250061 China)
The vibration suppression of switched reluctance motor (SRM) is a focused research area. This paper presented an improved method of magnetic field partition based on parabola arc formula to calculate the air-gap permeance of the SRM with complex rotor or stator profile. Then, a analytic calculation method on the weakened percentage of radial force wave was proposed, which adopted the ratio mode to calculate the reduction extent of radial force wave by changing the air-gap permeance. This method can provide a reference for vibration suppression design on changing stator or rotor profile. Taken a SRM with slotted rotor as an example, the magnetic field partition methods based on parabola and ellipse arc formula were used respectively to calculate winding inductance and the weakened percentage of radial force wave, which were validated by finite element analysis and prototype motor test. The results verified the improved method of magnetic field partition and the method on computing the weakened percentage of radial force wave.
Switched reluctance motor, air-gap permeance, magnetic field partition, slotted rotor, vibration reduction
TM351
高等学校博士学科点专项科研基金资助。
2014-04-14 改稿日期 2014-05-14
