变胞机构广义邻接矩阵运算法则的改进
2015-08-24孙志宏
张 浩, 孙志宏
(东华大学 纺织装备教育部工程研究中心, 上海 201620)
变胞机构广义邻接矩阵运算法则的改进
张浩, 孙志宏
(东华大学 纺织装备教育部工程研究中心, 上海 201620)
改进了变胞机构广义邻接矩阵的运算法则,运用新的运算法则,不仅可以得到变胞源机构,而且可以演绎出新的机构,丰富了变胞机构的内容.以精梳机钳板驱动机构为例,运用上述运算法则,演绎出变胞式钳板驱动机构,并通过运动分析证明了该机构运动的可行性,进一步验证了本文提出的运算法则的可行性.
变胞机构; 邻接矩阵; 矩阵运算; 精梳机; 钳板摆动机构
变胞机构(metamorphic mechanism )的研究[1]始于1997年,并于1999年公开发表[2],变胞机构借用了生物学中的“metamorphosis”,即变形、变拓扑、可生长进化演化的含义.其定义为:一个工作周期中,具有多个工作阶段,不同工作阶段的闭环运动链呈现不同的拓扑结构,配合其机架和原动件实现不同运动,称为变胞机构[3].变胞机构 “变”的因素体现在定义中所指出的3个“不同”,变胞机构中的“胞”是运动链,变胞机构的“胚”指的是拓扑结构,即不同拓扑结构状态在不同的运动阶段间的相互变化.变胞机构不同工作阶段的运动特性靠机构相应工作阶段的拓扑结构来实现.机构通过构件或运动副的变化来实现拓扑结构的变化,所以变胞机构属于变拓扑结构的机构[3].而文献[4]提出机构成为变胞机构必须同时具备两个判定条件,即变拓扑结构和变自由度.一个机构是变胞机构的充要条件是变拓扑结构并且变自由度,而两个条件其中之一只是变胞机构的必要条件.文献[4]对变胞机构的界定多了自由度的要求,这个看似严谨的结论也存着一定的不足.文献[5]提到由一个平面RSSR四杆机构,通过运动副方位变胞得到一空间RSSR四杆机构,其机构本身就是一个单自由度机构,变化前后的空间拓扑关系发生改变,而自由度并未发生变化,其应该是变胞机构的范畴.由此可见,对于变胞机构概念的定义还有待进一步完善.
作为变胞机构的一个分支,柔性变胞机构[6-7]被提出来,其具有自由度与结构变化以及自动组合重构的特点,在航天器结构与变形机器人中有着独特的应用,对这一基础问题进行研究具有十分重要的学术研究和实际应用价值.文献[3]总结分析了变胞机构的表达方式和运算规则.通常,采用邻接矩阵的形式来描述变胞机构的拓扑关系,通过邻接矩阵的运算可以得到新的拓扑结构,从而得到新的机构[8-10].但对于含有复合铰链机构的邻接矩阵的表示方法并不很完善,文献[11]提出了一些改进性的建议,但是其所提出的表示方法(在m个构件构成的复合铰链处用m个运动副表示)不满足机构自由度要求,有待进一步完善.
目前矩阵运算方法有两种:利用矩阵不同行或列中0和0,0和1,1和1相加,然后消除全为0的行或列[11];根据工作状态邻接矩阵的广义“并”运算,得到变胞源矩阵[3].针对后一种运算方法,由工作阶段邻接矩阵通过广义矩阵“并”运算直接得到变胞源矩阵,过于突然不便理解.为此,本文提出过渡变胞源矩阵的概念,对上述广义矩阵运算提出改进方法.然后通过对过渡变胞源矩阵的分析和分解,进一步得到变胞源矩阵,为求得变胞源机构提供新的研究思路.同时,本文提出一种变胞式钳板摆动机构,验证了该矩阵运算的可行性.
1 邻接矩阵的广义运算演绎
文献[3]提出用变胞方程的方法来研究变胞机构,并提出了矩阵的广义运算法则,该法则通过广义的“并”(U)运算,可以由机构工作阶段邻接矩阵得到一个综合机构所对应的变胞源矩阵.该运算法则原理:在构件编号和顺序保持不变的情况下,矩阵相对应的构件和运动副数目的子矩阵块进行“并”运算,即运动链邻接矩阵中“部分连续相同行和列”的子矩阵块产生“并”覆盖,原元素保留,不同元素则产生新的行和列,新的行和列分别是相“并”的矩阵不同的矩阵块的行和列,由左到右依次添加到新的矩阵上.图1(a)为曲柄摇杆机构,图1(b)为曲柄滑块机构,所对应机构的邻接矩阵,通过上述矩阵运算直接得到变胞源机构的邻接矩阵,如式(1)所示.
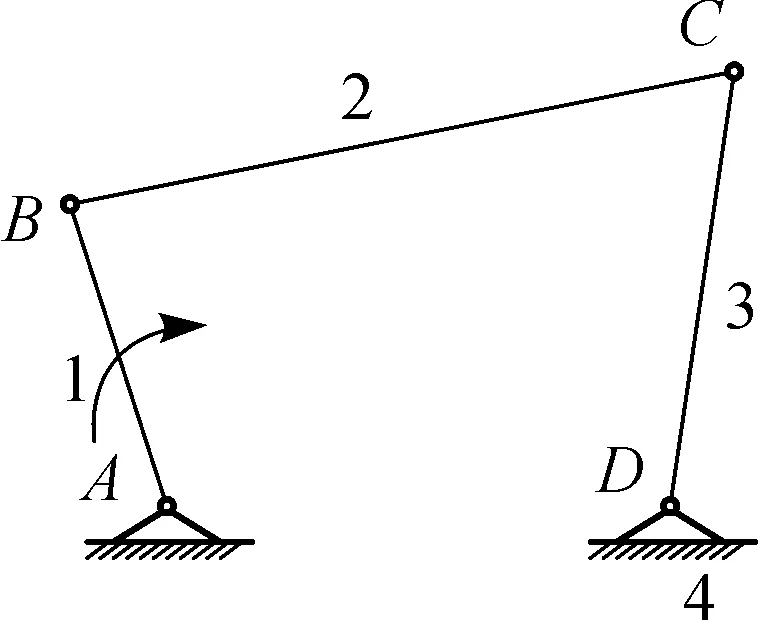
(a) 曲柄摇杆机构
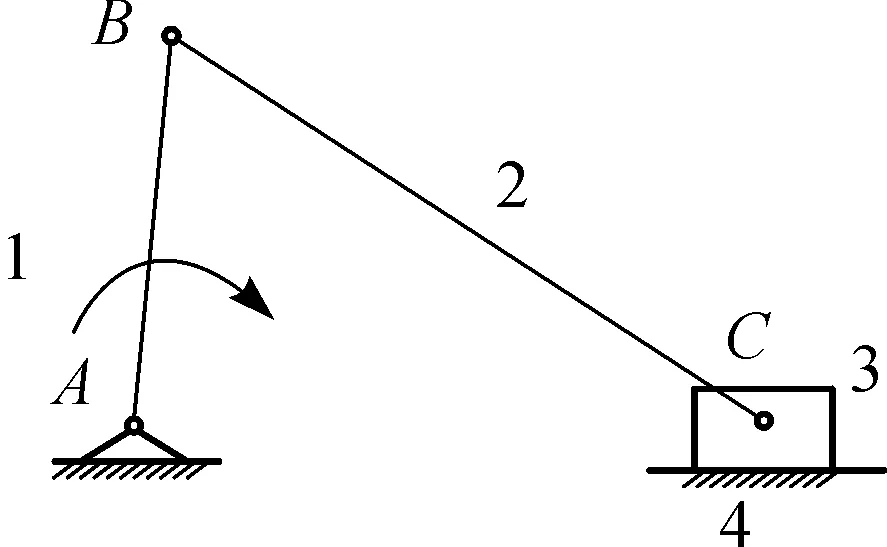
(b) 曲柄滑块机构
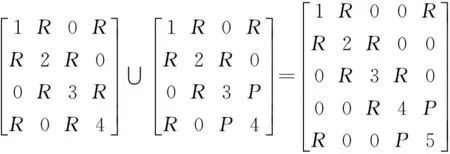
(1)
上述运算法则的表述不是很直观,在理解上有些难度.为了使这种“并”运算更容易理解,本文做了一定的改进,并通过图1所示机构的工作阶段邻接矩阵的运算,解释改进后的“并”运算法则.
首先,在不同工作阶段对应的邻接矩阵构件编号顺序(对角线)不变的前提下,对矩阵中的其余元素,按照其所对应相同的位置进行“并”运算.例如,在式(2)中
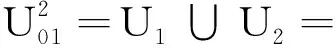
(2)
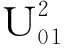
其次,对上述过渡变胞源矩阵“并”所在的位置进行分解,进而得到变胞源矩阵.分解过程如下所述.
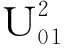
(2)如果构件数目发生改变,则变胞位置一定在构件3和4之间,此时变胞方式称为构件变胞.在构件3和4之间添加一个构件,对R∪P进行分解,可以得到两个变胞源矩阵分别为式(3)和(4),其所对应的变胞源机构分别如图2(c) 和2(d)所示.
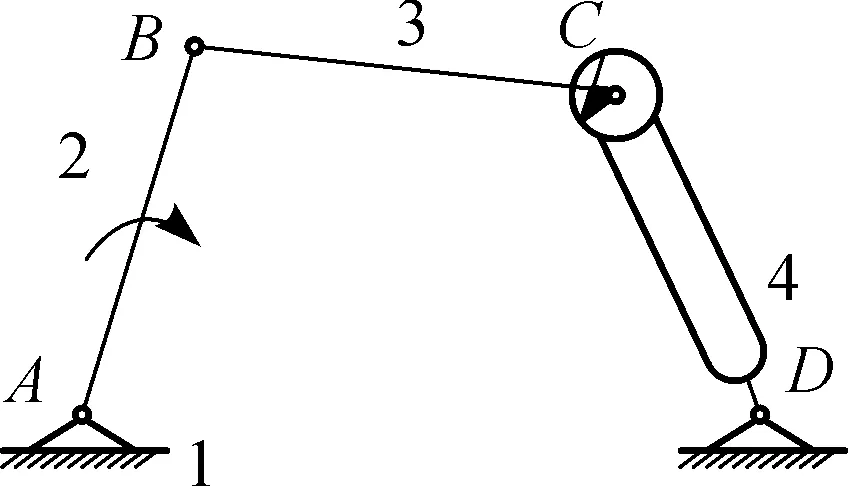
(a) 运动副变胞阶段1
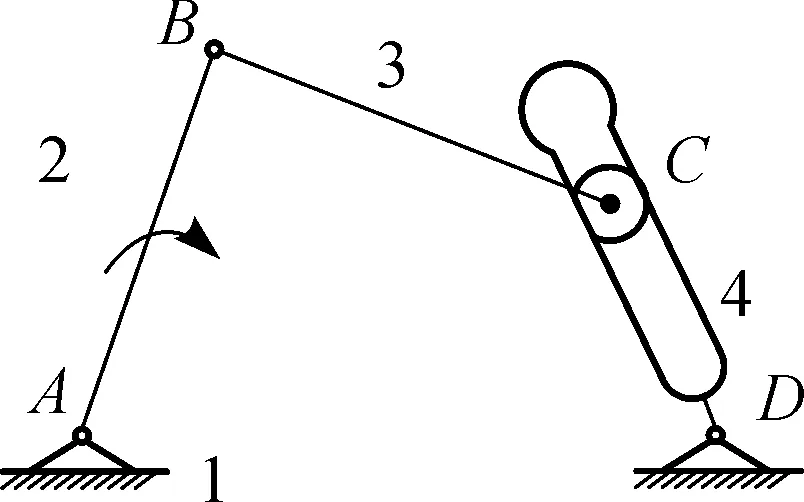
(b) 运动副变胞阶段2
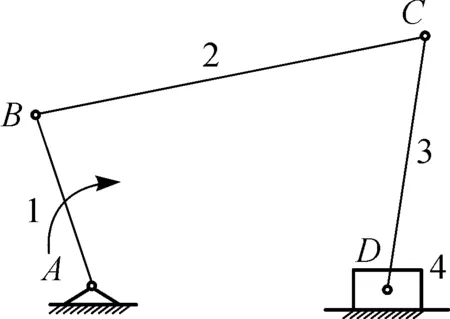
(c) 构件变胞1
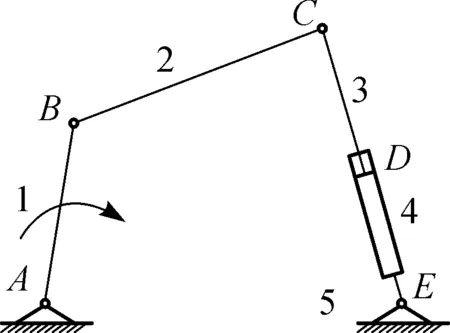
(d) 构件变胞2
(3)
(4)
文献[8]中给出的特种包装机械中的2自由度变胞机构也可以用此运算方法来解释.图3为这一变胞机构的两个工作状态.图3(a)为工作阶段1,此时构件3与机架固结成一个构件,凸轮机构中摆动从动件2绕C点往复摆动,实现送布缠绕运动;图3(b) 为工作阶段2,在该阶段构件2与3构成一个构件,盘状凸轮机构的直动从动件在凸轮推动下往复移动.
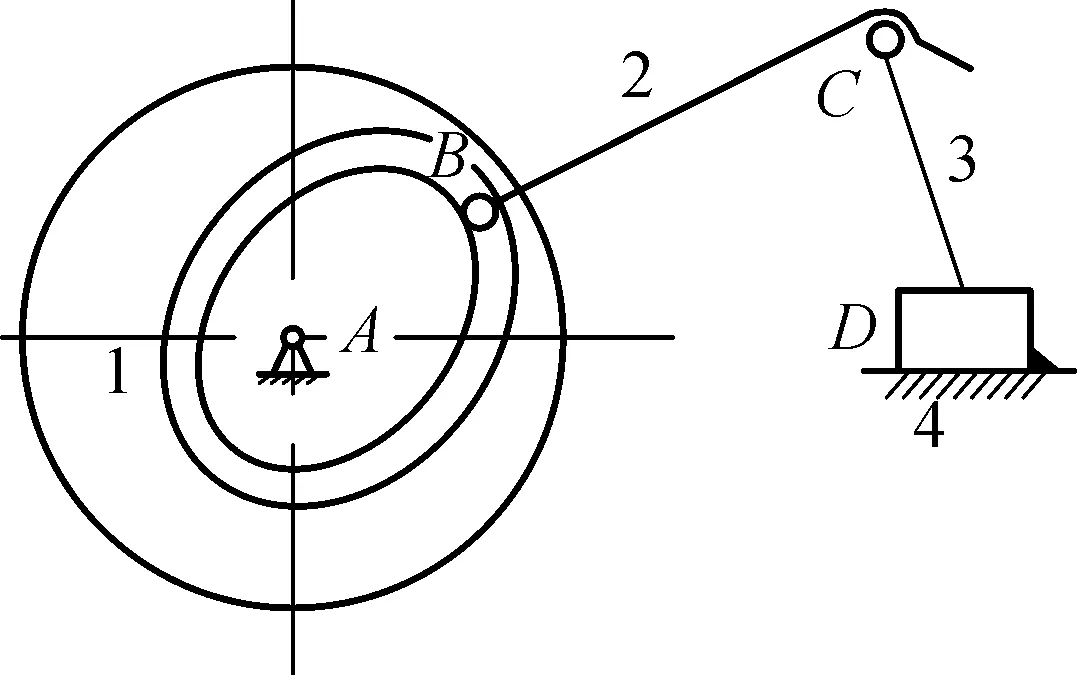
(a) 工作阶段1
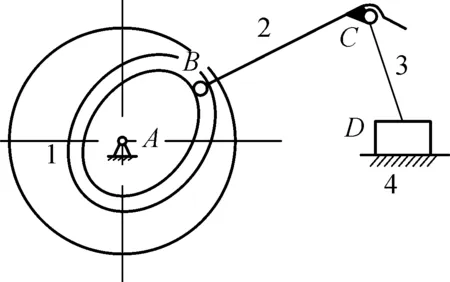
(b) 工作阶段2图3 特种包装机械的工作阶段Fig.3 Working stages of special packaging machinery
上述两个阶段机构所对应的邻接矩阵的形式分别如式(5)和(6)所示.
(5)
(6)
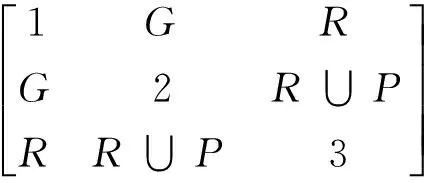
(7)
根据前面的矩阵运算过程,可得其过渡变胞源矩阵如式(7)所示,对此过渡变胞源矩阵进行分析和分解如下所述.
对刀误差△T,如图1因是铣多孔,铣孔尺寸为φ5F7±0.020铣刀尺寸为φ5±0.03mm,尺寸40±0.1mm的对刀误差均为铣刀与导向槽的最大间隙。
(1) 如果在变胞前后构件数目不发生变化,而仅仅是运动副产生变化,则过渡变胞源矩阵即是变胞源矩阵.根据邻接矩阵的形式可以得到新的机构如图4(a)所示.
(2) 如果变胞前后构件数目发生改变,则构件变化的位置一定在构件2和3之间.在构件2和3之间加上一个构件,并对R∪P进行分配,即可得到如式(8)和 (9)两种形式的变胞源矩阵,它们所对应的机构简图分别如图4(b)和4(c)所示.
(8)
(9)
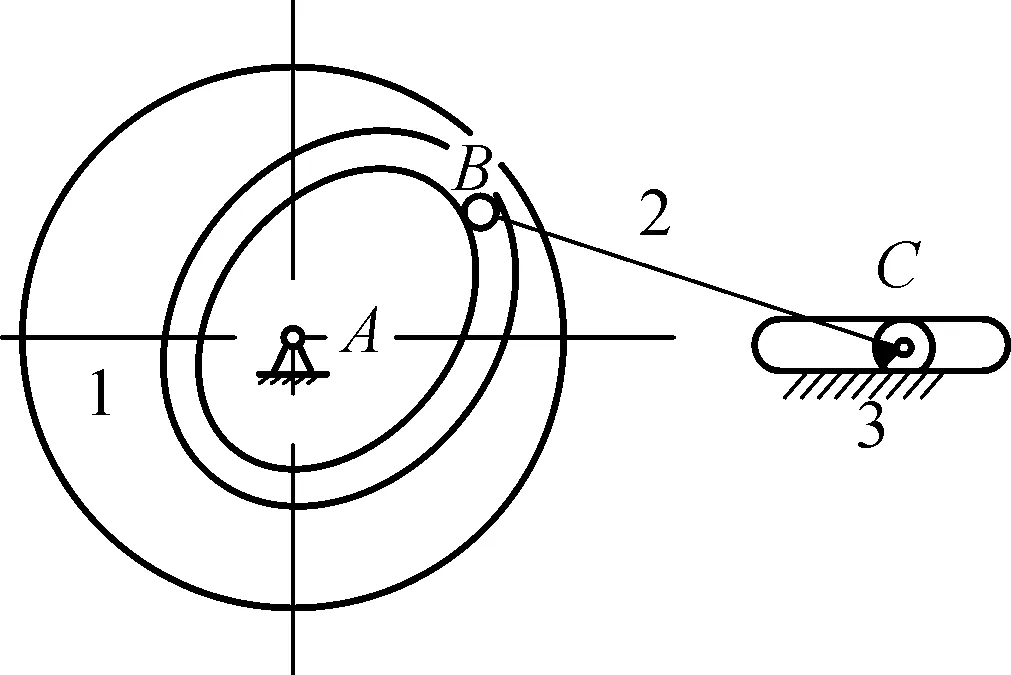
(a) 运动副变胞
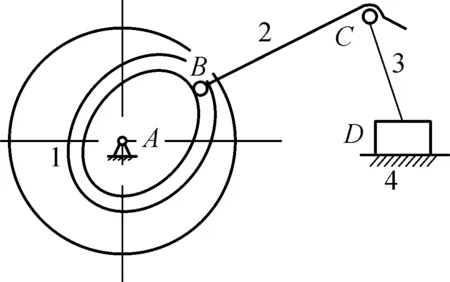
(b) 构件变胞1
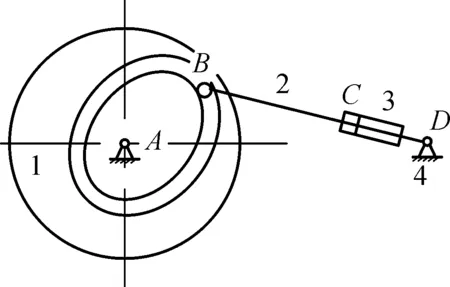
(c) 构件变胞2图4 变胞源机构Fig.4 Metamorphic source mechanism
2 具有变胞功能的精梳机钳板摆动机构设计
精梳机中钳板摆动机构的运动特性为钳板的摆动和钳板的开口与闭合运动所构成的平面运动.这两种简单的运动方式所构成的机构可以采用变胞机构来实现.
2.1精梳机钳板摆动机构的运动方式
精梳机中钳板摆动机构如图5(a)所示[12].下钳板3固定安装在下钳板座4上,钳板摆臂5固定安装在钳板摆轴6上,钳板摆臂2固定安装在锡林轴1上,它们是以钳板摆轴和锡林轴为支点所构成的四连杆机构.当锡林带动法兰转动一周时,由于构件间的连接,使钳板摆轴做来回摆动,通过钳板摆臂5和下钳板座4,使钳板做前后摆动.上钳板架7连接在下钳板座4上,上钳板8固定安装在上钳板架7上,偏心轮11安装在张力轴12上,偏心轮的轴套装在导杆10上端,上钳板架7与导杆10下端铰接,钳板钳口加压弹簧9装在导杆上.其运动分析过程如下:推程时,钳板摆轴6逆时针转动,钳板向前摆动,张力轴12也做逆时针方向回转,再配合导杆10和装于其上的弹簧9的拉伸,使上钳板8逐渐开口;回程时,钳板摆轴6顺时针方向转动,钳板向后摆动,张力轴也做顺时针转动,在导杆10及下钳板座4的共同作用下,上钳板8逐渐闭合.钳板闭合后,下钳板3继续向后移动,导杆中的弹簧9受压使导杆缩短,进而对钳板钳口施加压力,使钳板有效地握持棉丛等待锡林梳理.图5(b)为其机构运动简图.
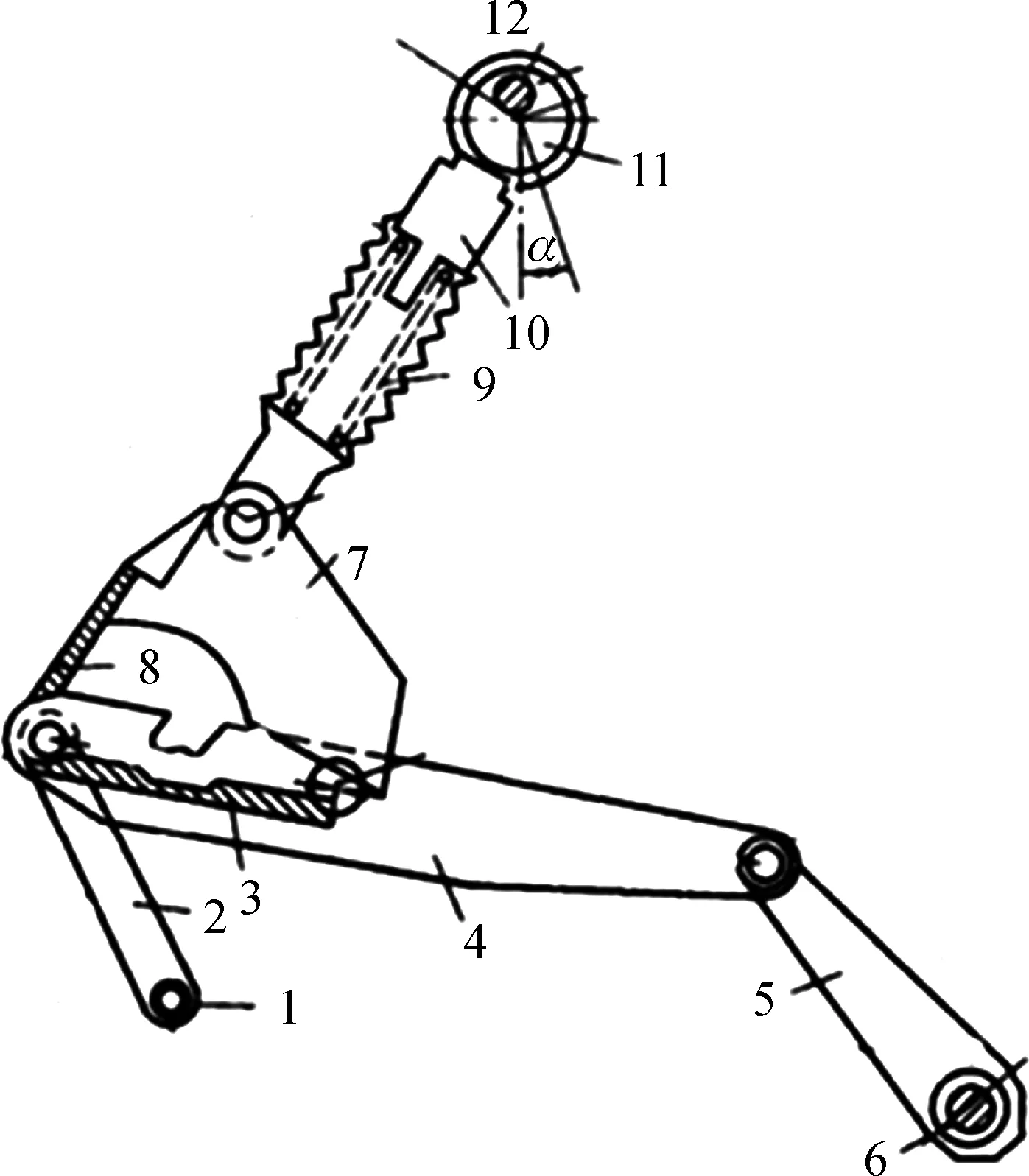
(a) 精梳机钳板摆动机构
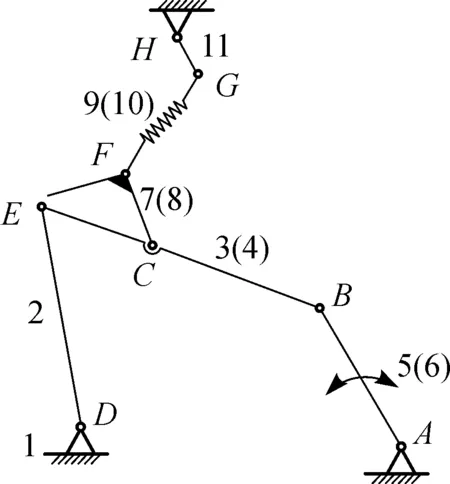
(b) 机构简图图5 钳板摆动机构及其简图Fig.5 Nipper swing mechanism and diagram
精梳机的一个运动周期分为4个阶段,其钳板的运动特点如下所述.第一阶段:锡林梳理阶段,上钳板8与下钳板3闭合,钳板先向后再向前运动;第二阶段:分离前准备阶段,上、下钳板由闭合逐渐开启,钳板继续向前运动;第三阶段:分离结合阶段,上、下钳板开口逐渐增大并继续向前运动;第四阶段:锡林梳理前的准备阶段,上、下钳板向后摆动,逐渐闭合.
2.2变胞式钳板摆动机构
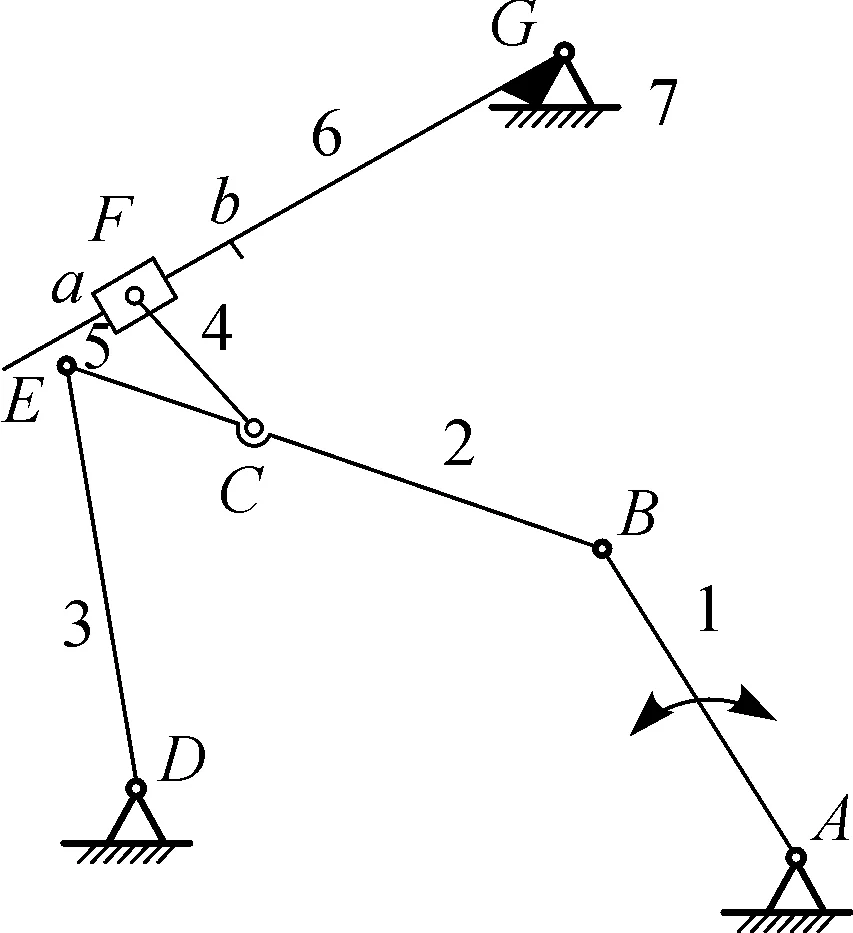
(a) 钳板摆动阶段
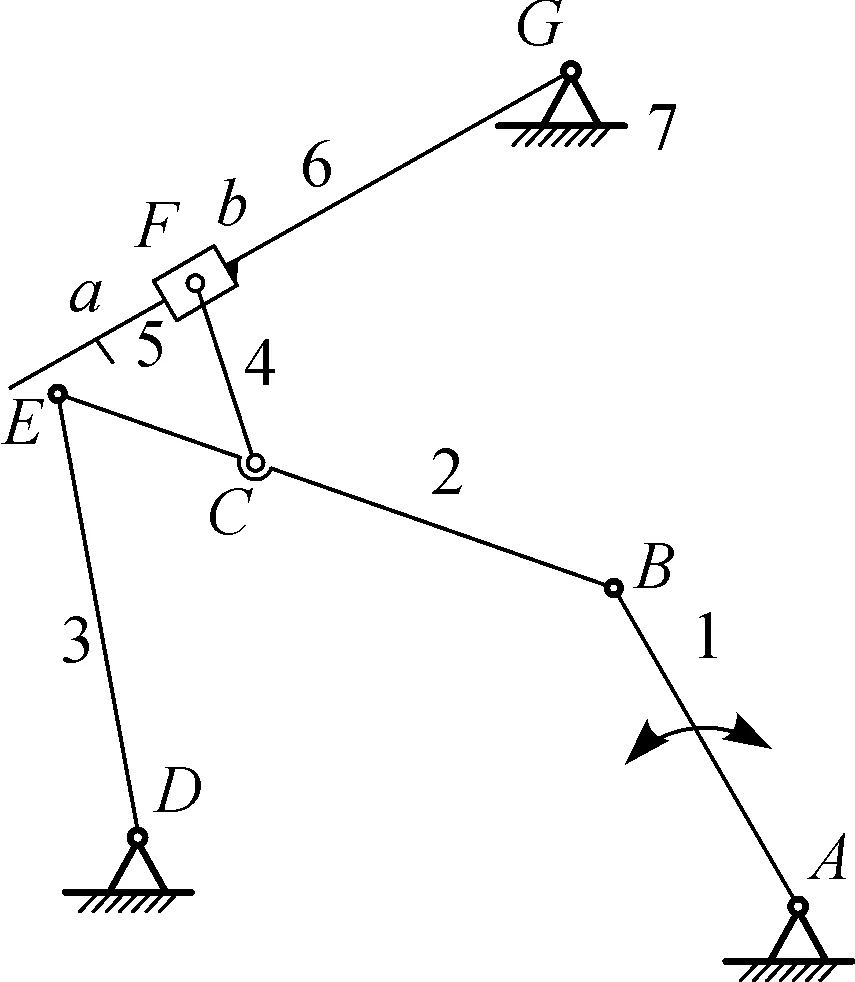
(b) 钳板开启阶段
通过对上述机构的运动分析,可以得到图6(a)和6(b)所对应的邻接矩阵分别如式(10)和(11)所示.
(10)
(11)
采用第1节矩阵的运算方法可以得到钳板摆动机构的变胞源机构的过渡变胞源矩阵如式(12)所示.
U01=U1∪U2=
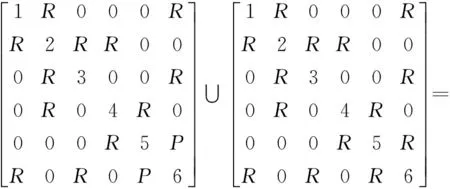

(12)
同样,变胞源机构的分析如下所述.
(1) 如果变胞前后构件数目不发生变化,而仅仅是运动副在不同的工作阶段发生变化,则过渡变胞源矩阵即是变胞源矩阵.根据邻接矩阵的形式可以得到新的机构形式如图7(a)所示.
(2) 如果构件数目发生改变,则构件变化的位置一定在构件5和6之间.在构件5和6之间加上一个构件,对R∪P进行分配,即可得到如式(13)和 (14)两种形式的变胞源矩阵,它们所对应的机构简图分别如图7(b)和7(c)所示.
(13)
(14)
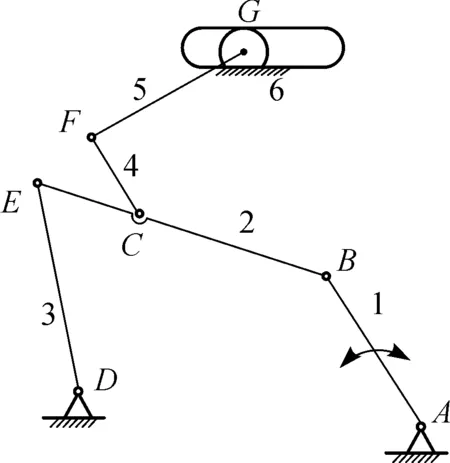
(a) 运动副变胞
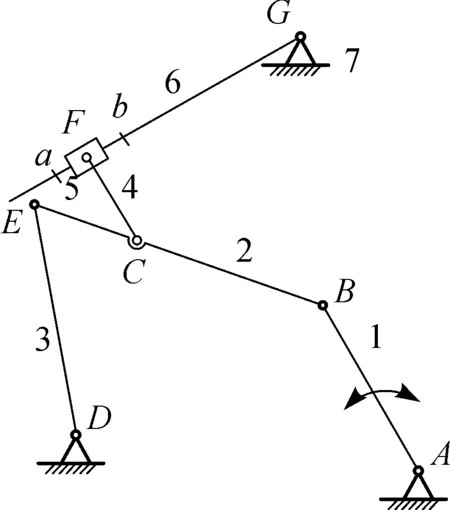
(b) 构件变胞1
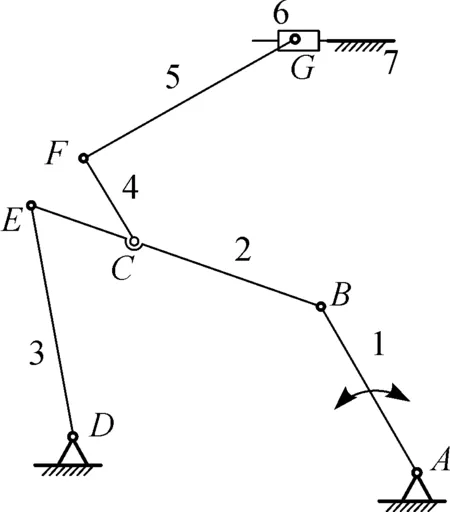
(c) 构件变胞2图7 变胞源机构Fig.7 Metamorphic source mechanism
通过上面分析,得到3种具有变胞功能的精梳机钳板摆动机构的变胞源机构.在以上的基础上,通过详细的尺寸设计能够产生新的精梳机中钳板摆动驱动机构.
3 结 语
通过对变胞机构邻接矩阵广义算法的研究,本文得到的结论如下所述.
(1) 提出了关于广义邻接矩阵运算方法的改进措施.通过改进后的运算方法,不仅可以得到变胞源机构所对应的变胞源矩阵,而且可以得到新的变胞源矩阵,根据邻接矩阵的形式,可以得到新的拓扑结构.这种方法为变胞机构以后的研究提供了一个新思路.
(2) 提出了一种具有变胞功能的精梳机钳板摆动机构的设计.将现有精梳机钳板摆动机构的运动过程分解成两个单独的运动过程,每一个运动过程用一个简单的机构来表示.然后运用新的矩阵运算法则,将两个单独的运动过程所对应的邻接矩阵组合成一个综合机构所对应的邻接矩阵,通过对邻接矩阵的分析和分解,即可得到变胞式精梳机钳板摆动机构.同时,通过运动分析也进一步验证了新的矩阵运算法则的可行性.
[1] DAI J S, REES J J. Theory on kinematics synthesis and motion analysis of equivalent mechanisms [R].Unilever Research, 1997.
[2] DAI J S, REES J J. Mobility in metamorphic mechanisms of foldable/erectable kinds [J]. Transaction of ASME, Journal of Mechanical Design, 1999, 121(3):375-382.
[3] 王德伦,戴建生.变胞机构及其综合的理论基础[J].中国机械工程学报,2007,43(8):32-42.
[4] 李端玲,张忠海,戴建生,等.变胞机构的研究综述与展望[J].机械工程学报,2010,46(13):14-19.
[5] 李树军,戴建生.变胞机构的构态变换矩阵与运动副方位变胞[J].机械工程学报,2010,21(14):1698-1703.
[6] 丁希仑,戴建生.柔性变胞机构的研究与展望[J].中南大学学报:自然科学版,2005,36(1):211-215.
[7] 李东福,金国光.柔性变胞机构动力学研究[D].天津:天津工业大学机械工程学院,2007:1-62.
[8] 戴建生,丁希仑,王德伦.一空间变胞机构拓扑结构的变换和对应的矩阵演算[J].中国机械工程学报,2005,41(8):30-35.
[9] 吴艳荣,金国光,李东福,等.描述变胞机构构态变换的邻接矩阵法[J].机械工程学报,2007,43(7):23-26.
[10] 杨飞,陶建国,邓宗全.描述变胞机构构态变换的一种新方法及其在构型综合中的应用[J].机械工程学报,2011,47(15):1-8.
[11] LI D L, ZHANG Z H. Configuration analysis of metamorphic mechanisms based on extended adjacency matrix operation[J]. Chinese Journal of Mechanical Engineering, 2011, 24(5): 767-773.
[12] 郁崇文.纺纱系统与设备[M].北京:中国纺织出版社, 2005:87-88.
Improvement on the Operation Rule of Metamorphic Mechanism Generalized Adjacent Matrix
ZHANGHao,SUNZhi-hong
(Engineering Research Center of Advanced Textile Machinery, Ministry of Education,Donghua University, Shanghai 201620, China)
The operation rule of metamorphic mechanism generalized adjacent matrix was improved. According to the new operation rule, not only metamorphic source mechanism can be obtained, but also new mechanisms can be deduced to enrich the content of metamorphic mechanism. Taking the nipper swing mechanism in a comber as an example, a metamorphic nipper swing mechanism was got by using this operation rule. The feasibility of the improved mechanism was proved by motion analysis.
metamorphic mechanism; adjacent matrix; matrix operation; comber; nipper swing mechanism
1671-0444(2015)06-0802-06
2014-09-25
张浩(1991—),男,安徽阜阳人,硕士研究生,研究方向为机构分析与设计.E-mail: 310543794@qq.com
孙志宏(联系人),女,教授,E-mail: zhsun@dhu.edu.cn
TH 112
A
