一种新的自组织粒子群聚类算法

刘世华，叶展翔，刘向华（温州职业技术学院 信息技术系，浙江 温州 325035）

一种新的自组织粒子群聚类算法

刘世华，叶展翔，刘向华
（温州职业技术学院 信息技术系，浙江 温州 325035）

针对粒子群优化（PSO）算法复杂度偏高的问题，提出一种新的基于竞争学习的自组织粒子群聚类（SOPSC）算法。该算法采用每个粒子代表一个聚类中心的编码方法，通过借鉴自组织映射（SOM）算法的竞争学习机制，采用类内相似度和类间相异度作为指导，使粒子进行自组织飞行，从而达到自动聚类的目的，克服了传统粒子群聚类算法中粒子编码复杂、算法复杂度偏高的缺点。实验证明，该算法聚类精度高、稳定性好，且对初始值和参数不敏感。

粒子群聚类；竞争学习；PSO；SOM；SOPSC

DOI：10.13669/j.cnki.33-1276/z.2015.059

1　概 述

随着群体智能算法的发展及其广泛应用，各种智能算法广泛应用于数据聚类，粒子群优化（PSO）算法就是其中重要的一种。2002年Omran等提出一种基于粒子群优化的无指导图像分类算法［1］，这被认为是最早提出的基于PSO的聚类算法。之后的粒子群聚类算法大都遵循其基本思想［2］。2003年Merwe等在此算法基础上提出了基本PSO算法［3］，用于对一般数据集进行聚类操作。同时，他们还研究了PSO算法与传统K-means算法相结合的混合聚类算法，经实验发现，混合方法部分改进了K-means算法容易陷入局部最优的缺点，但该算法复杂度偏高［2-3］。这是由于基本的粒子群聚类每个粒子代表一个数据划分（聚类结果），导致单个粒子编码的维度过大造成的。随后，人们又将粒子群与模糊C均值算法进行结合用以改进算法效率。李峻金等对粒子群聚类算法进行了综述，介绍了后续的一些改进工作［2］。刘春晓对PSO算法进行了大量实验研究，并提出一种基于自组织映射（SOM）神经网络和PSO的聚类组合算法，即SOM/PSO算法，该算法利用SOM的聚类结果初始化P S O的粒子位置，可以减少聚类算法的收敛时间，提高聚类精度［4］。

目前，所有的PSO算法及其改进都没有对粒子编码进行简化，它们均采用一个粒子代表一个全局聚类中心的编码方式。如果待聚类数据每个数据点有n维，将聚类成k类，那么每个粒子就需要至少n×k维的向量来进行编码，直接导致了PSO算法的复杂度偏高。为有效解决这一问题，本文提出一种新的基于竞争学习的自组织粒子群聚类（Self-organized PSO Clustering，简称SOPSC）算法。SOPSC算法将每个粒子编码为一个聚类中心点，每个粒子只需要n维，共投放k个粒子即可，在粒子飞行时，引入SOM算法中的“胜者为王”（Winner-takes-all，简称WTA）的竞争学习机制，并通过类内相似度和类间相异度特征进行引导，从而提高PS O算法的效率。实验证明，该算法聚类效果好于K-Means算法和PSO算法，算法稳定性好，每次都能收敛到较好的全局最优解，对初始值和参数不敏感，且聚类效率高于PSO算法。

2　粒子群聚类算法

PSO算法的基本思想是通过群体中个体之间的协作和信息共享来迭代式地寻找最优解。在每一次的迭代中，粒子通过跟踪两个最优解来指导自己的下一步行动：一个是粒子本身所找到的最优解，称为个体极值（Pbest）；另一个是整个种群目前找到的最优解，称为全局极值（Gbest）。

根据以上两个最优解，标准粒子群算法通过（1）、（2）式来更新自己的移动速度和位置，即：

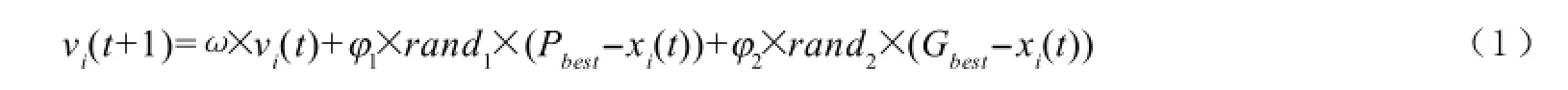
（1）式为速度更新公式。其中，vi（t+1）是第t+1次迭代时第i个粒子移动的速度，ω为惯性权重，φ1，φ2为局部最优和全局最优的调节权值。

（2）式为位置更新公式，即t+1次迭代中粒子i的位置为第t次的当前位置加上速度更新。

粒子群中的每个粒子都代表待求解的优化问题的一个解，根据速度和位置的更新准则，粒子将最终收敛于一个全局最优解。

根据PSO算法的基本思路，传统的PSO算法根据数据点的维数n和待聚类的簇数目k，对每个粒子进行n×k维编码，每个粒子代表一个聚类划分，其k个聚类的中心点体现在粒子编码中，如图1所示。

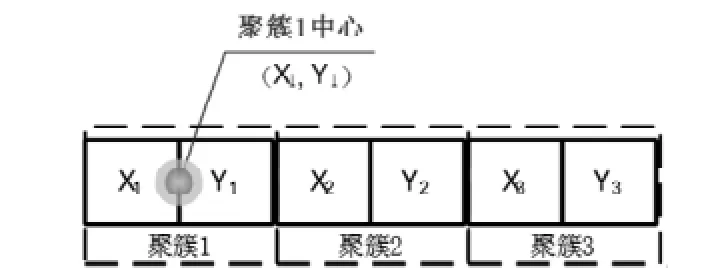
注：假设n=2，k=3。图1　PSO算法的粒子编码

每个粒子在寻求局部最优和全局最优解时应遵循以下适应度函数f：

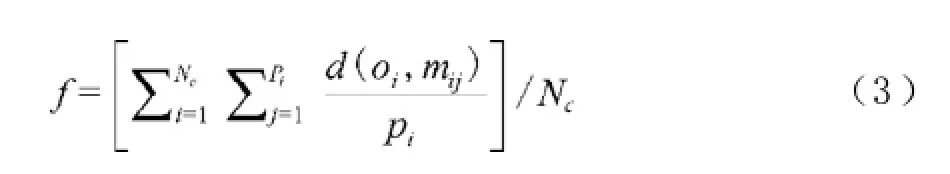
其中，pi为属于第Ci个类的样本数，Nc为聚类簇数目，oi为第i个类的中心，mij为属于第i个类的第j个样本，d（x，y）为x与y的距离度量。

传统的PSO算法将聚类问题看成优化问题，然后采用粒子群优化策略来进行求解，能够较好地获得全局最优解，但由于其粒子编码采用n×k维，当数据的维度增加或聚类数目较大时，粒子的编码维度急剧增加，这使得PSO算法计算复杂度太高而影响其实用性。

3　自组织粒子群聚类算法

3.1SOM神经网络与竞争学习

（1）SOM神经网络。SOM神经网络是芬兰Helsink大学的Kohonen教授于1981年提出的，又称Kohonen网。Kohonen认为，一个神经网络接受外界输入模式时，将会分为不同的对应区域，各区域对输入模式具有不同的响应特征，且这个过程是自动完成的［5］。

自组织竞争型神经网络是一种无教师监督学习，具有自组织功能的神经网络。它通过自身的训练，可以自动对输入模式进行分类，在网络结构上，一般由输入层和竞争层构成两层网络，两层网络之间各神经元实现双向连接，且网络没有隐含层，有时竞争层各神经元之间还存在横向连接，如图2所示。

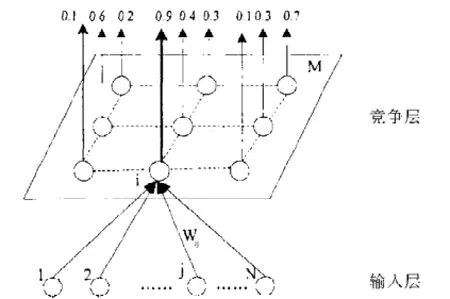
图2　SOM神经网络模型

自组织竞争型神经网络构成的基本思想是：网络的竞争层各神经元竞争对输入模式响应的机会，最后仅有一个神经元成为竞争的胜者，这一获胜神经元则表示对输入模式的分类。如果H为空间的连续输入数据，A为空间的离散输出空间，Ф为特征映射的非线性变换，它映射输入空间H到输出空间A表示为：Ф：H→A。

如果给定输入向量X，SOM神经网络首先根据特征映射Ф确定其在输出空间A中的最佳匹配神经元i。神经元i的突触权值向量Wi可以视为神经元指向输入空间X的映射。

在SOM网络模型中，每一个权系数向量都可以看作是输入向量在神经网络中的一种内部表示，或者说，它是输入向量的映像，其自组织功能的目的就是通过调整权系数，使神经网络收敛于一种表示形态。

（2）竞争学习原理。SOM神经网络成功的关键就是其竞争学习方法。网络的输出神经元之间相互竞争以求被激活，结果在每一时刻只有一个输出神经元被激活。这个被激活的神经元称为“竞争获胜神经元”，而其它神经元的状态被抑制，故称为“胜者为王”。

竞争学习过程主要有以下三个步骤：

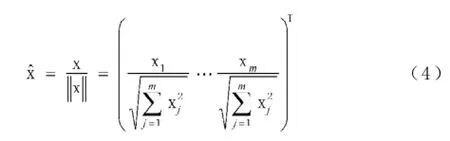
步骤1：将当前输入模式向量X和竞争层中各神经元对应的权重向量Wj（j=1，2，…，m，表示m个竞争神经元）全部进行归一化处理，即：

步骤2：通过计算输入向量和m个竞争神经元的内积竞选出获胜神经元j*，使其符合：

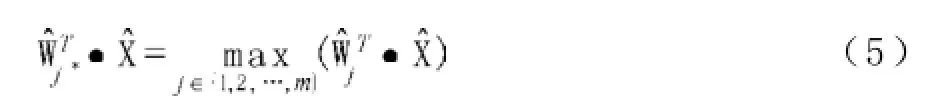
步骤3：对获胜神经元权重Wj*和学习率η进行调整，直到学习率η为0，学习结束，即：

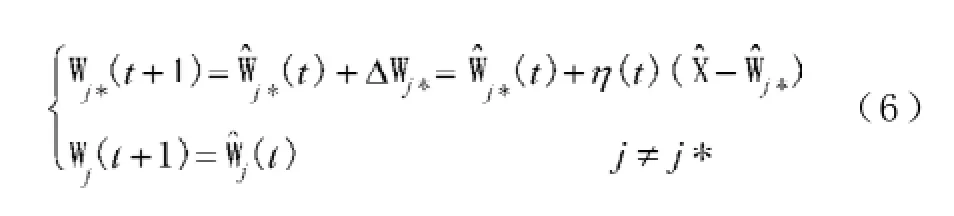
其中学习率η是一个小于1的依次递减的参数，用于确保算法的收敛。

3.2SOPSC算法

SOPSC算法引入了竞争学习的思想，并对传统PSO算法进行了改良，简化了每个粒子的编码，将每个粒子编码为一个聚类中心，即每个粒子只代表某一类的中心点，同时对粒子的位置和速度更新规则进行设定。

（1）局部最优部分Pbest，采用聚类中心点来代表，即聚类中心点作为当前簇中粒子应到达的最优位置，如果有新的数据点加入该聚类，则需更新该簇中的粒子和该聚类中心点Pbest。

（2）由于每个粒子编码只代表一个聚类中心，聚类迭代过程中无法确定每一个聚类中心的全局最优位置，因而新算法中取消全局最优部分Gb es t。

（3）对于一次循环中未获胜的粒子，出于保持类间相异度考虑，将这些粒子对照获胜粒子进行反弹移动操作，即让其他粒子远离获胜中心点。

（4）对于在整个迭代过程中一直都没有获胜的粒子，直接将其转移到类内相似度比较小（欧式距离比较大）的粒子附近，让其下一轮参与该区域的竞争，使其用于将原来聚类数据点较多的簇进一步区分。

SOPSC算法伪代码如下：

其中，f（x）为在x所在聚类簇中，以x为中心点计算均方差的值，以此来判断x在聚类中的中心性；xmax_dist（t）为类内相似度比较小（欧式距离比较大）的粒子的当前位置；distance（yi，xj）用于计算输入点yi与粒子xj的欧式距离。

4　实验验证

为验证算法的有效性，首先采用Ruspini数据集进行初步实验，并给出原始数据点分布，采用SOP SC的粒子分布和K-Means算法聚类的簇中心点分布的直观图示观察算法的稳定性；然后采用UCI的Iris数据集进行实际数据的聚类验证，分别采用两种算法运行100次，比较它们的平均结果和算法稳定性；同时，针对SOPSC算法，通过实验分析算法中权重参数和初始值对聚类结果的影响。实验证明，SOPSC算法聚类精度高、稳定性好，且对初始值和参数不敏感，是一种理想可行的聚类算法。

4.1Ruspini数据集的直观验证实验

Ruspini数据集是一个有75个二维数据点的数据集，分为4类，分别有20、23、17和15个数据点，主要用于进行模糊聚类算法的评估。Ruspini数据集原始数据分布如图3所示。

采用K-means算法k=4时对正规化后的数据进行聚类，从运行结果看，K-means算法稳定性不高，比较容易受到初始值的影响，其较好和较差结果如图4所示。

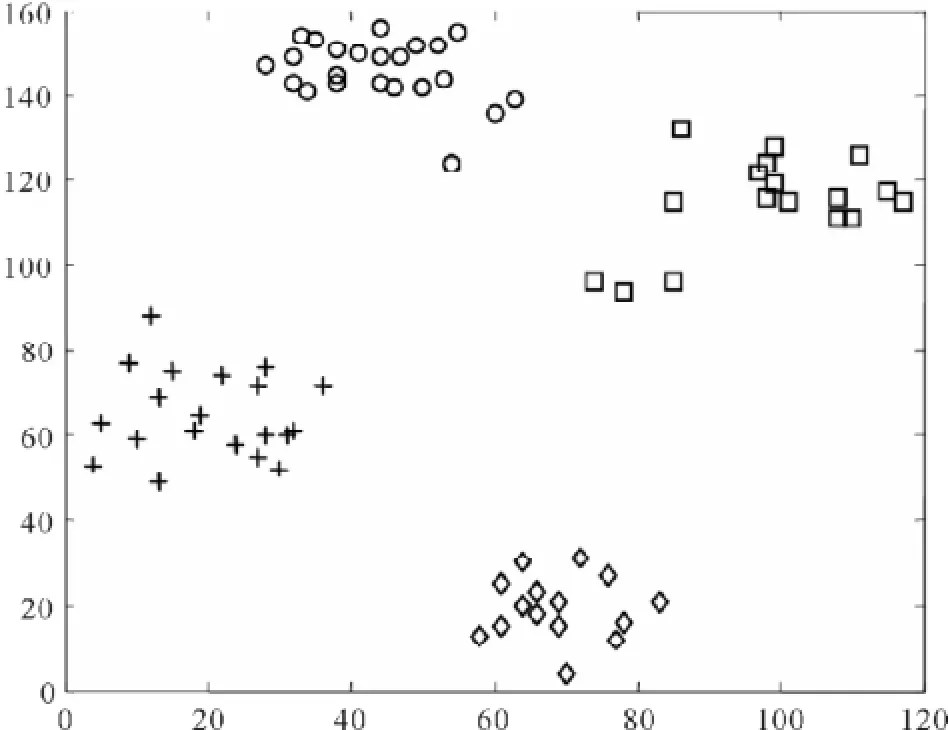
图3　Ruspini数据集原始数据分布

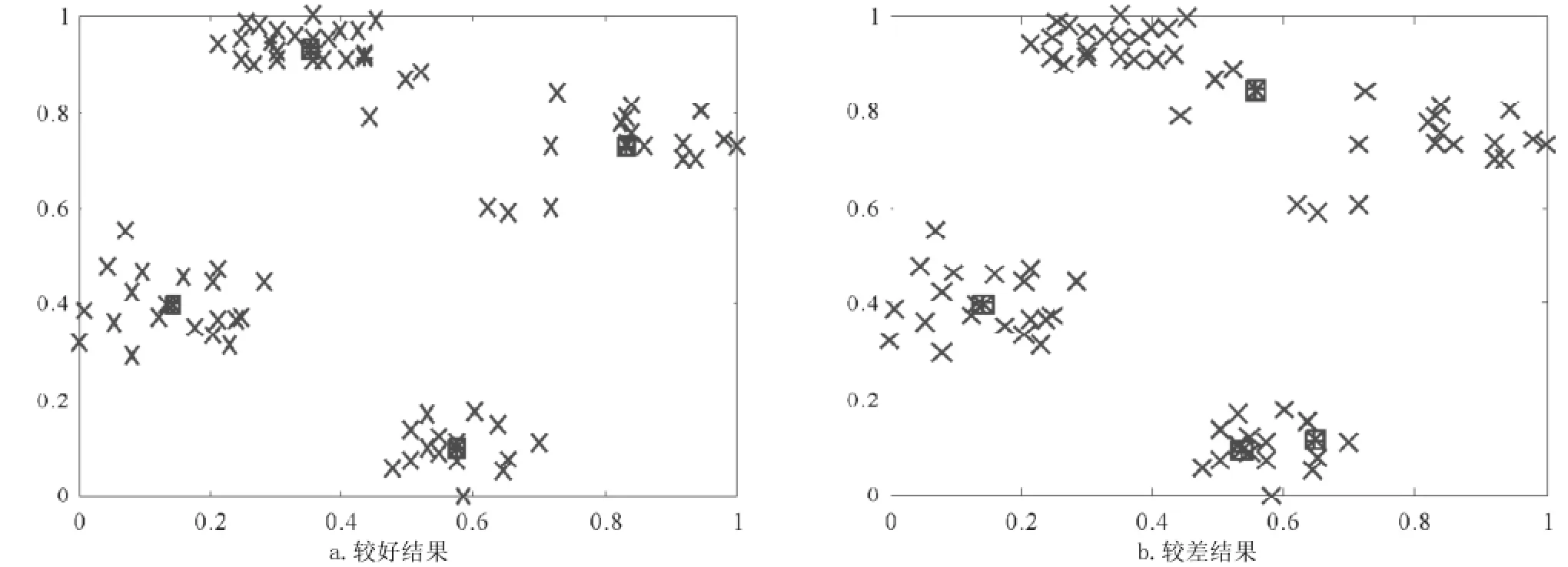
图4　K-means聚类中心分布情况

采用SOPSC算法，使用4个粒子，全部放在中心位置，vmax=0.01，ω=0.95，算法迭代100次。在进行聚类前，将数据集中的点进行线性缩放，将数据点的坐标值全部映射到［0，1］区间。此时，SOPSC粒子分布情况如图5所示。

由Ruspini数据集已知数据点的分类情况，因而可以比较两种聚类算法的聚类正确性。从实际聚类结果看，SOPSC算法的聚类正确率在每次运行时当迭代次数在20次以上即可达到100%；而K-Means聚类算法在初始值分布不理想时，效果很差，从多次重复试验结果看，平均每运行5~6次，才出现1次最优结果，其最优结果能达到100%。

4.2真实数据集的聚类比较实验

为进一步验证算法的实用性，采用UCI提供的Iris数据集进行聚类实验。Iris数据集是以鸢尾花的特征作为数据来源的真实世界的数据，有150个四维的数据点，分为3类，每类50个数据。实验采用Weka平台进行，每种聚类算法运行100次取平均值。

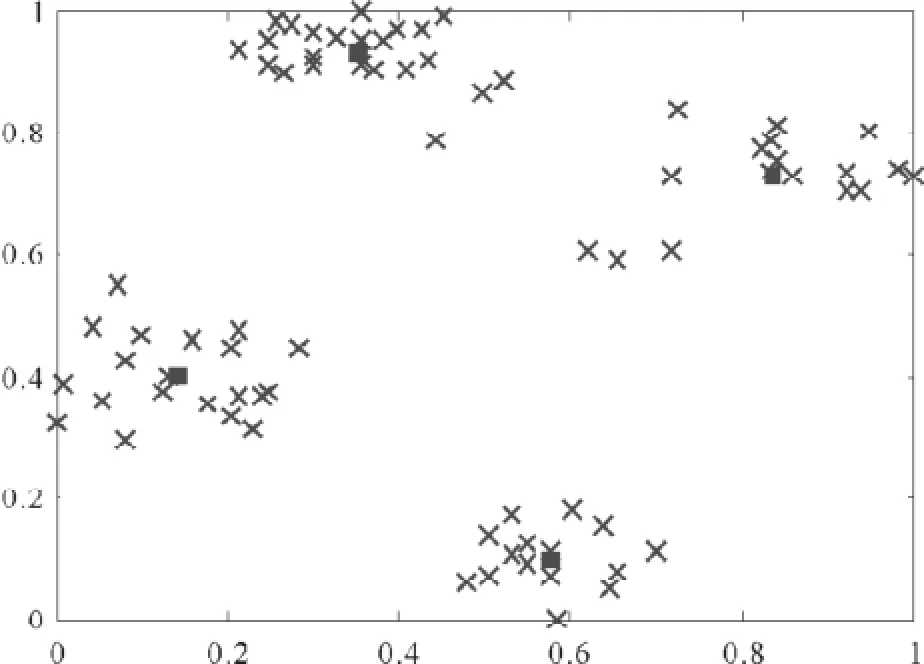
图5　SOPSC粒子分布情况

分别采用K-Means算法和SOPSC算法对Iris数据集进行聚类，并比较它们聚类后的聚类正确性、类内相似度和类间相异度。

（1）聚类正确性采用简单比较所分的三类中的数据点数目的正确性和计算聚类正确率来度量。聚类正确率ACC定义为正确聚类的数据点数除以总数据点数。

（2）类内相似度采用均方差（即同一簇中数据点到数据中心点的距离的平方和除以数据点数）来度量，第k类的类内相似度记为Simk，即：

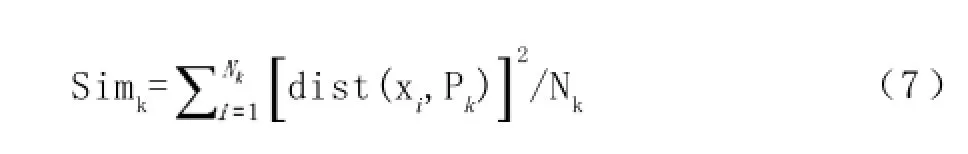
其中，Nk为属于第k个聚类簇中数据点数目，Pk为第k个聚类簇的中心点。dist（xi，Pk）为第i个数据点与第k个聚类中心的距离。类内相似度Simk数值越小，表示聚类效果越好。

（3）类间相异度采用聚类中心点的距离和来度量，记为Diff，即：

由表1可以看出，在Iris数据集上，SOPSC算法的表现略好于传统的K-Means算法，但也没有象在Ruspini数据集上的表现一样达到100%。K-Means算法在某一二次运行中能够得到近似100%的效果，但由于受初始值影响比较大，其平均效果也受到影响。

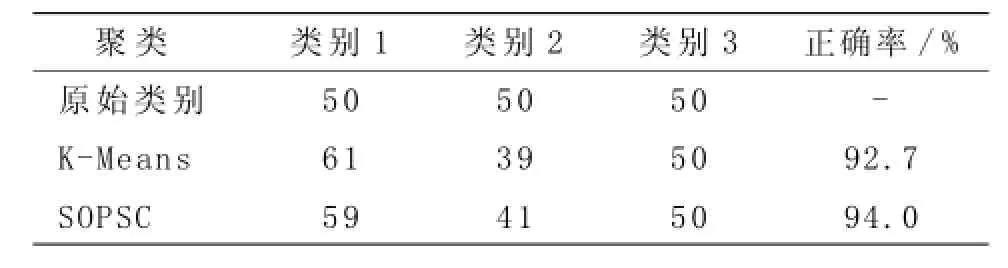
表1　Iris聚类正确性

类内相似度和类间相异度计算结果见表2。其计算是基于对原始数据进行线性缩放归一化到［0，1］范围内进行，与直接在原始数据上进行聚类和计算的结果不同。聚类的目的就是要根据样本一定的相似特征进行分组，并使代表类内相似度的参数Simk最小化（Simk越小表示类内的数据点越相似），使类间的相异度最大化（即聚类中心隔得越远越好）。由表2可以看出，SOPSC算法在类内相似度上结果优于传统的K-Means算法，而类间相异度则比传统的K-Means算法略胜一筹。

表2　类内相似度和类间相异度计算结果

在SOPSC算法中，局部最优和输入向量在速度更新中的权重φ1，φ2分别取［0，1］之间的随机数即可，对其聚类结果没有影响。从本质上看，SOPSC算法如果把输入向量yj部分的影响去除，即如果取φ1=1，φ2=0，则SOPSC算法与K-Means算法是一样的，因而SOPSC算法也可以看成是对K-Means算法的一种泛化，它只是在K-Means算法的基础上增加了随机扰动和当前输入向量的影响。

5　结 论

本文对自组织粒子群聚类（SOPSC）算法进行了初步的研究和实验分析。从直观验证实验可以看出，SOPSC算法较K-Means算法稳定。SOPSC算法继承了PSO算法的全局寻优特性，同时融合了S OM算法中的竞争学习自组织特性，解决了传统P SO算法复杂度偏高的缺点。从真实数据集的聚类比较实验可以看出，SOPSC算法在聚类精度上优于传统的K-Means算法，虽然前者算法时间和复杂度比后者高，但相较于传统的PSO算法有了较大提高，粒子编码复杂度有所降低，长度由n×k变成了n。下一步将研究该算法用于实现聚类数目的自动确定、孤立点检测和实现不同形状簇的聚类等问题。

［1］Omran M，Salman A，Engelbrecht A P.Image classification using particle swarm optimization［C］//Proceedings of the4th Asia-Pacific Conference on Simulated Evolution and Learning.Piscataway：IEEE Press，2002：370-374.

［2］李峻金，向阳，芦英明，等.粒子群聚类算法综述［J］.计算机应用研究，2009，26（12）：4423-4427.

［3］Merwe D D.Data Clustering using Particle Swarm Optimization［C］//Proceedings of IEEE Congress on Evolutionary Computation. Canberra：IEEE Press，2003：215-220.

［4］刘春晓.基于SOM和PSO的聚类算法研究［D］.成都：西南交通大学信息科学与技术学院，2009.

［5］Kohonen T.Self-organized Formation of Topologically Correct Feature Maps［J］.Biological cybernetics，1982，43（1）：59-69.

［责任编辑：田启明］

A New Self-Organized PSO Clustering Algorithm

LIU Shihua， YE Zhanxiang， LIU Xianghua
（Information Technology Department， Wenzhou Vocational & Technical College， Wenzhou，325035， China）

A Self-organized PSO Clustering （SOPSC） algorithm based on competition learning was proposed against the complexity of PSO clustering algorithm. The algorithm coded one particle as a center of each cluster for clustering analysis. Through the competition learning of SOM algorithm， particles flew as self-organized manner directed by the inner similarity and dissimilarity between different clusters to achieve the goal of self-clustering. It overcame the complexity of particle coding and algorithm of traditional PSO clustering. It was tested that the algorithm improves the cluster accuracy and its stability and is not sensitive to the initial value and parameters.

PSO clustering； Competition learning； PSO； SOM； SOPSC

TP311.13

A

1671-4326（2015）03-0054-05

2014-05-14

温州职业技术学院科研项目（WZY2014032）

刘世华（1978—），男，江西永丰人，温州职业技术学院信息技术系讲师，高级工程师，硕士；叶展翔（1971—），男，浙江温州人，温州职业技术学院信息技术系，高级工程师，硕士；刘向华（1980—），女，湖南隆回人，温州职业技术学院信息技术系讲师，硕士.