生猪养殖场的经营管理策略

成宝娟（咸宁职业技术学院 工学院，湖北 咸宁 437100）

生猪养殖场的经营管理策略

成宝娟
（咸宁职业技术学院 工学院，湖北 咸宁 437100）

以2014年高教社杯全国大学生数学建模竞赛C题为背景，针对生猪养殖场的经营管理问题，要求利用自己的种猪自行繁衍，提供最佳经营管理策略，求出生猪养殖场的最大利润。从合理化的角度对养猪过程进行分析，建立线性规划模型，结合所收集的数据给出最佳经营管理策略，使养猪利润最大化。

生猪养殖；盈亏平衡点；母猪；存栏数；极值点

DOI：10.13669/j.cnki.33-1276/z.2015.039

1　问题的提出

2014年高教社杯全国大学生数学建模竞赛C题“生猪养殖场的经营管理”给出了养猪的一般过程，已知生猪养殖场最多存栏数为10 000头，要求利用自己的种猪进行繁育，建立数学模型并回答以下问题：

（1）不出售猪苗时，要达到或超过盈亏平衡点，每头母猪每年平均产仔量要达到多少？

（2）求使得该养殖场养殖规模达到饱和时，小猪选为种猪的比例和母猪的存栏数。

（3）假设已知三年内生猪价格变化的预测曲线，请根据价格预测确定该养殖场的最佳经营管理策略，计算这三年内的平均年利润，并给出在此策略下的母猪及肉猪存栏数曲线。

2　模型假设与符号说明

2.1模型假设条件

将每年的时间分割成两个周期，即一个周期为半年；刚出生的母猪半年后可以进行配种，母猪的生育期为4年，共生育8胎；种猪在出生4年半后失去生育能力，被无害化处理；养殖场经过4年半的养殖后，已经处于近似稳定状态；假设无害化处理每头猪补贴80元；成年种母猪失去生育能力后全部进行无害化处理；养殖场存栏数最多为10 000头。本文主要研究4年半后养殖场的经营状况，即从第10个周期开始，因而模型中i的取值范围为：i=10，11，12，…

2.2符号说明

注：本文是在2 0 1 4年高教社杯全国大学生数学建模竞赛荣获国家级二等奖的基础上改编而成，竟赛指导老师为成宝娟。

n为每头母猪每胎产量（头），m为养殖场成年母

猪的数量（头），Li为第i个周期养殖场的利润（元），qi1为第i个周期乳猪的数量（头），qi2为第i个周期猪苗的数量（头），qi3为第i个周期肉猪的数量（头），qi4为第i个周期新增种猪的数量（头），k为种猪中母猪的比例（%），p1为一只肉猪出生后的平均可变成本（元/头），p2为一只种猪一个周期内的平均可变成本（元/头），p4为一只猪苗出生后一个周期内的平均可变成本（元/头），p5为一只猪苗出售的平均价格（元/头），p3为一只肉猪出售的平均价格（元/头），C0为养殖场的固定成本（元），q为成年种猪的数量（头）。

3　模型的建立与求解

3.1问题1的求解

3.1.1模型1：在不出售猪苗的条件下，qi2=0。假设不考虑种猪的死亡和由于意外、疾病等特殊原因而失去生育能力的情况，养殖场的利润等于收益减去成本［1］，收益为肉猪出售的收益加上无害化处理种猪补贴的费用。肉猪出售的收益等于肉猪头数乘以每头肉猪的价格，即qi3p3，无害化处理每头猪补贴80元［2］，无害化处理种猪补贴的收益等于无害化处理猪的数量乘以每头无害化处理补贴的价格，即80qi4，则总收益为qi3p3+ 80qi-9，4。而成本函数为固定成本C0加上可变成本C1，可变成本等于肉猪的可变成本加上种猪的可变成本，其中肉猪的可变成本等于每头肉猪的可变成本乘以肉猪的数量，即qi3p1。后备种猪的存栏数为qi4，成年种猪的存栏数为前8个周期的后备种猪的存栏数，即：。如果不考虑种猪的死亡和由于意外、疾病等特殊原因而失去生育能力的情况，则种猪的存栏数等于后备种猪的存栏数加上成年种猪的存栏数为：

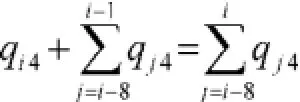
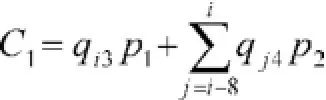
总成本为：

总利润等于总收益减去总成本，故总利润为：要使达到或超过盈亏平衡点，则：

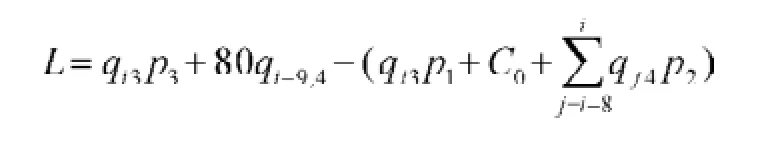
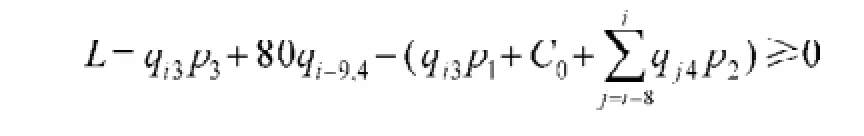
于是得到方程组：

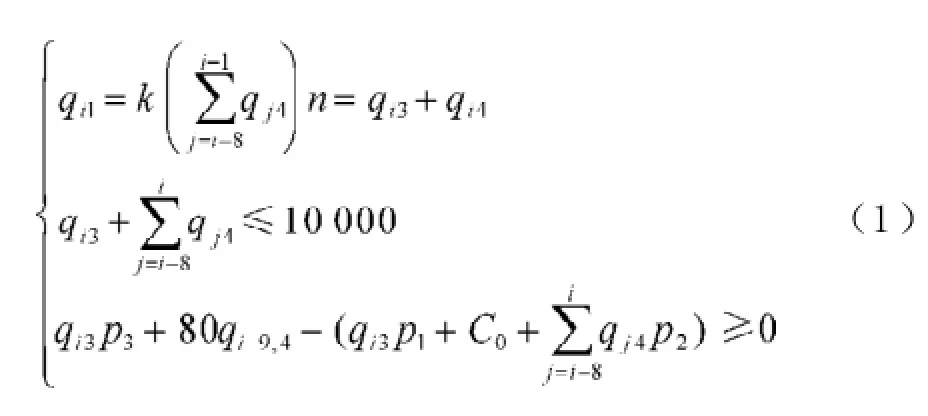
为了简化以上方程组，假设养殖场从第10个周期起，已经处于近似稳定状态，每个周期新增种猪的数量相同，即qi4为一常数。于是（1）式简化为：

从而求出n的范围为：

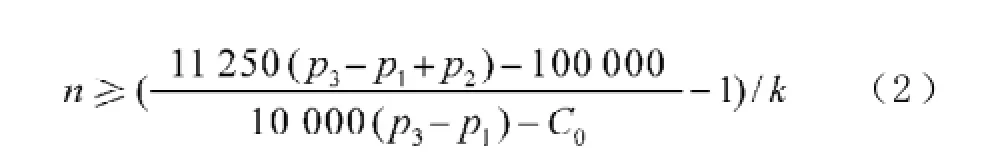
养殖场半年内的固定成本包括猪舍、设备购置及安装费用、三通一平及基本设施费用，猪场内绿化及污水处理（水沟等）费用，以及其他配套投资等，估计总固定成本为50万元［3］，即C0=5×105。经调查，一只肉猪大约100kg时出售，价格大约为14元/kg，故一只肉猪的收益大约为1 400元，即p3=1 400元/头；估计一头肉猪出生后的可变成本为950元，即p1=950元/头，估计一只种母猪一个周期内的可变成本为2 400元。

在自然交配为主的猪场，公母种猪比例为1：20～1：2 5；在人工交配为主的猪场，公母种猪比例为1：200～1：400［4］。因为公猪的比率非常小，故用一只母猪一个周期内的可变成本代替一只公猪一个周期内的可变成本，故p2=2 400元/头。

将p1=950（元/头），p2=2 400（元/头），p3=1 400（元/头），C0=5×105代入（2）式，在自然交配为主的猪场，种猪中母猪的比例大约为，解得n≥7.3。由于每头母猪一年可以产2胎，故每头母猪每年平均产仔量要达到2n=14.6头，才能达到或超过盈亏平衡点。在人工交配为主的猪场，种猪中母猪的比例大约为，解得n≥7.01，即每头母猪每年平均产仔量要达到2n= 14.02头，才能达到或超过盈亏平衡点。

3.1.2模型2：从第10个周期起，养殖场已经处于近似稳定状态。假设每年养的肉猪和种猪的数量相同，种猪中的公猪和母猪的比例也近似相同，即qi3为一个常数，qi4也为一个常数。其中母猪的生育期一般为3～5年，失去生育能力的公猪和母猪都会被无害化处理，所以估计母猪的生育期为4年，出生后的半年为生长发育期，即一个周期为后备母猪，4年半后母猪被无害化处理。经调查，一年内成年种猪在怀孕、生育、哺乳等过程中由于意外、疾病等特殊原因而失去生育能力及过了生育期而失去生育能力的比例大约为3 3%，半年内成年种猪在怀孕、生育、哺乳等过程中由于意外、疾病等特殊原因而失去生育能力及过了生育期而失去生育能力的比例大约为16.5%。这些种猪都将被无害化处理，每半年被无害化处理的种猪为0.165q，故生存下来的有生育能力的成年种猪的数量为0.835q，每半年新增后备种猪数量为0.165q。

为了争取最大化利润，假设养殖场存栏数为10 000头，而养殖场的存栏数=猪苗数+肉猪数+后备种猪数+种猪数，即10 000=qi3+0.165q+q。养殖场的乳猪数=猪苗数+肉猪数+后备种猪数，即qi1=qi3+0.165q。养殖场的乳猪数=成年母猪数×母猪一胎生育的数量，即qi1= qnk。

该养殖场养殖达到规模时，联立以上三个方程可得：

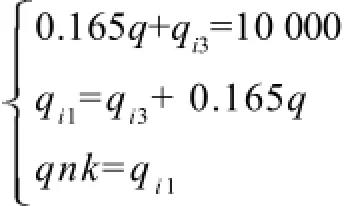
解得：

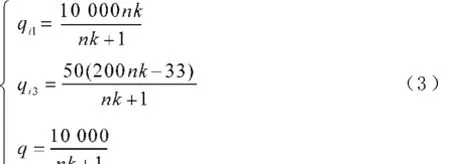
总收益为肉猪出售的收益和失去生育能力的种猪被无公害化处理的补贴之和，即：

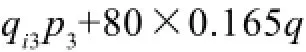
总成本为固定成本、肉猪的可变成本、种猪的可变成本之和，即：

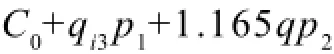
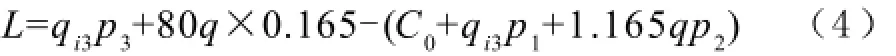
总利润为总收益减去总成本，即：要达到或超过盈亏平衡点，则L≥0。

将（3）式代入（4）式，解得：

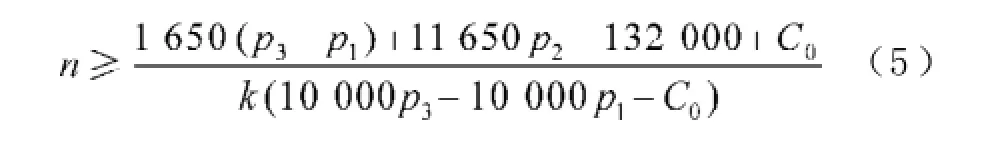
将p1=950（元/头），p2=2 400（元/头），p3=1 400（元/头），C0=5×105代入（5）式，当选择自然交配时，，解得n≥7.6，即每头母猪每年平均产仔量要达到2n=15.2头，才能达到或超过盈亏平衡点；当选择人工交配时，，解得n≥7.3，即每头母猪每年平均产仔量要达到2n=14.6头，才能达到或超过盈亏平衡点。

3.2问题2的求解

3.2.1模型3：假设母猪每胎成活9头左右，即n=9。养殖场处于近似稳定状态，假设每年养的肉猪和种猪的数量相同，种猪中的公猪和母猪的比例也近似相同，即qi3为一个常数，qi4也为一个常数。估计母猪有半年的生长发育期和4年的生育期，4年半后母猪被无害化处理。

养殖场的存栏数=猪苗数+肉猪数+后备种猪数+种猪数，即10 000=qi2+qi3+0.165q+q。养殖场的乳猪数=猪苗数+肉猪数+后备种猪数，即qi1=qi2+qi3+ 0.165q。养殖场的乳猪数=成年母猪数×母猪一胎生育的数量，即qi1=qnk。

联立以上三个方程可得：

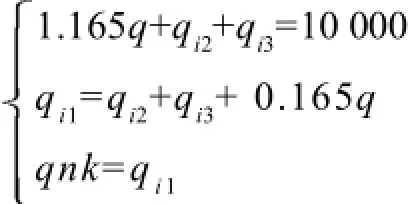
解得：

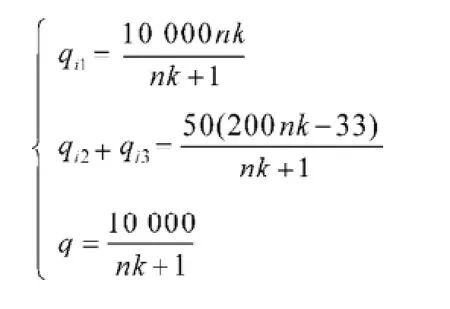
3.2.2模型4：

3.2.2.1假设养殖场种猪中成年母种猪为m头，计算以下各项指标：

（1）养殖场年出栏数。生育期母猪每头年产2胎左右，每胎成活9头左右。据调查，小猪在生长过程中的成活出栏率为92%。每头成年母猪年提供商品猪数为2×9×92%≈16.6头。一年内养殖场全部成年母猪提供的出栏猪数=成年母猪头数×一头成年母猪提供的出栏猪数。则该养殖场年出栏数为16.6m头，半年出栏数为8.3m头。

（2）公猪数。公猪数=成年母猪总数×公母比例。当采取自然配种时，公猪数为；当采取人工授精时，公猪数为。

（3）后备母猪数。一年后备母猪数=成年母猪数×一年更新率=m×33%；半年后备母猪数=成年母猪数×半年更新率=m×33%×0.5。

（4）后备公猪数。后备公猪数=成年公猪数×年更新率。当采取自然配种时，一年后备公猪数=× 33%，半年后备公猪数=×33%×0.5。当采取人工授精时，一年后备公猪数=×33%，半年后备公猪数=× 33%×0.5。

（5）一年内猪苗数+肉猪=全年出栏量16.6m；半年内猪苗数+肉猪=全年出栏量的一半，即×16.6= 8.3m。

3.2.2.2计算小猪选为种猪的比例和母猪的存栏数。养殖场常年存栏数=成年母猪数+成年公猪数+半年内后备母猪数+半年内后备公猪数+半年内猪苗数+半年内肉猪数。

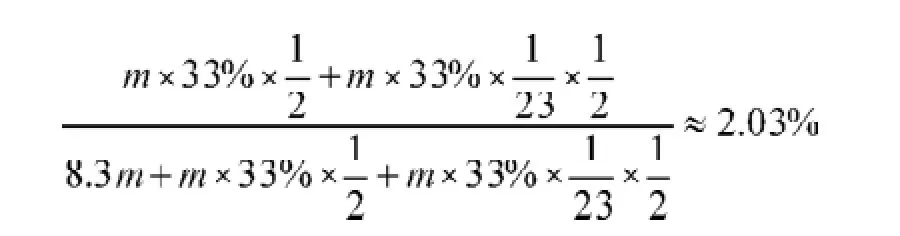
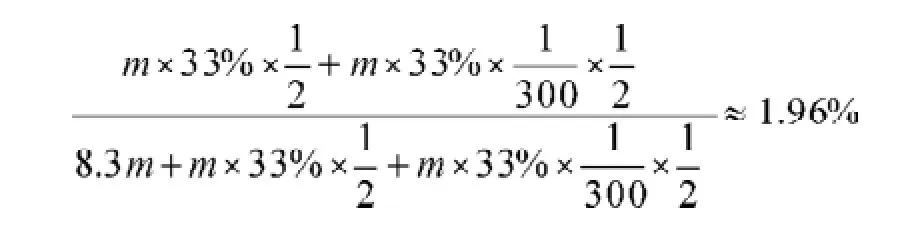
3.3问题3的求解

模型5：生猪养殖主要考虑以下三个因素：一是母猪最佳配种时间。母猪最佳配种时间为10—12月和4—6月。母猪在温暖、凉爽的气候条件下生产，休养生息好、体况恢复快，且小仔猪的成活率、增重率也因气温适宜得到大大提高。二是母猪的繁衍性能。一般情况下156天/胎次（其中空怀7天，妊娠114天，哺乳35天），两次妊娠的时间间隔最小为156天，一般大约在半年左右。三是利润最大化。根据题目给出的生猪价格三年预测曲线，为了追求利润最大化，应尽量选在曲线的极大值点处或其附近，这样生猪价格越大，利润则越大。生猪最佳出售时间点如图1所示。

考虑到养殖场种猪配种的时间分配和工作人员的合理安排，假定一个周期内的配种时间为一个月，即母猪的配种时间选为4—6月中的一个月和1 0—12月中的一个月。考虑到市场的供需关系，养殖场宰猪的时间分配、工作人员的合理安排和市场的生猪价格，假定一个周期内出售生猪的时间大约为一个月。

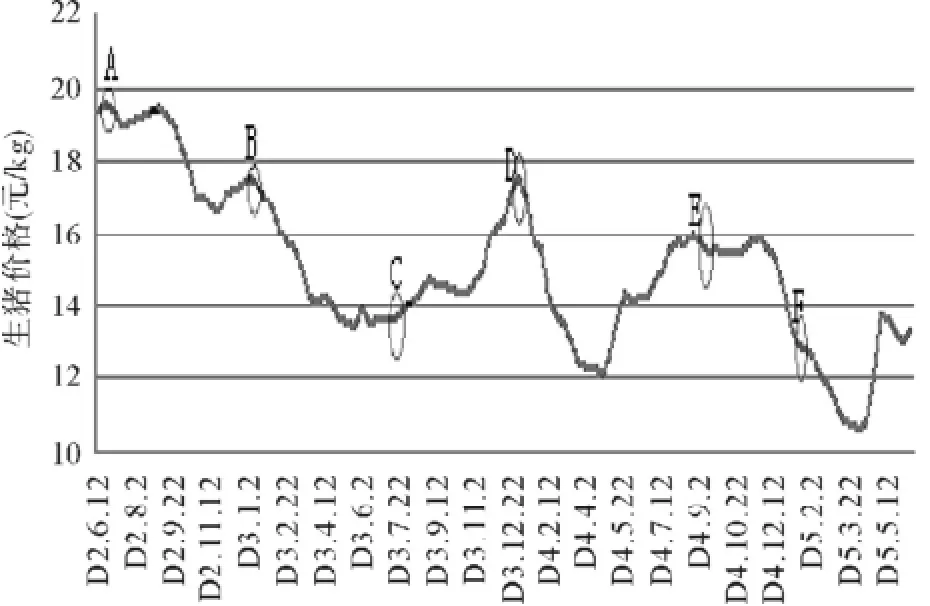
图1　生猪最佳出售时间点

由图1可以看出，A，B，D，E点为极大值点，故在这些点的两旁依次取15天出售肉猪。其中，C点右边的点较高，而左边的点较低，为了追求利润最大化，选择C点左边5天，右边25天出售肉猪；F点左边的点较高，而右边的点较低，为了追求利润最大化，选择F点左边25天，右边5天出售肉猪。生猪最佳配种、出售时间段见表1。

根据问题2算出的结果，估计养殖场成年种猪数为1 000头，后备种猪数为200头，猪苗数和肉猪数大约为8 800头，收益为肉猪出售的收益加上无害化处理种猪补贴的费用及猪苗出售的费用。肉猪出售的收益为qi3p3，无害化处理每头猪补贴80元，无害化处理种猪补贴为80q×0.165，猪苗出售的收益为qi2p4，则总收益为qi3p3+80q×0.165+qi2p4。而成本函数为固定成本C0加上可变成本C1，可变成本等于肉猪的可变成本加上种猪的可变成本加猪苗的可变成本。肉猪的可变成本为qi3p1。后备种猪的存栏数为0.165q，种猪的存栏数等于后备种猪的存栏数加上成年种猪的存栏数，即1.165q，种猪的可变成本为1.165qp2。可变成本C1=qi3p1+ 1.165qp2+qi2p4，总成本C=C0+C1=C0+qi3p1+1.165qp2+ qi2p4。总利润等于总收益减去总成本，即L=qi3p3+80q× 0.165+qi2p5-（C0+qi3p1+1.165qp2+qi2p4）。

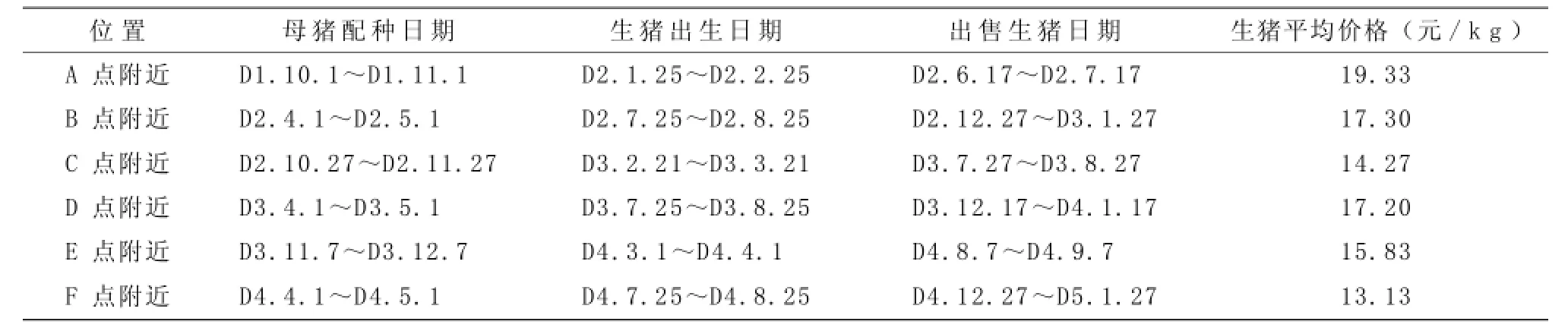
表1　生猪最佳配种、出售时间段

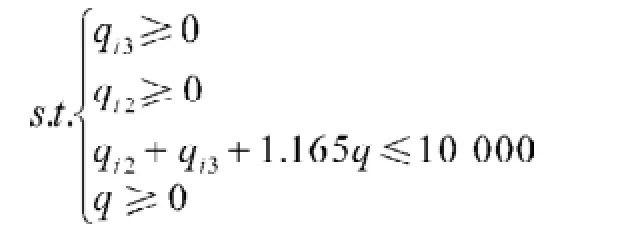
假设猪苗育肥饲养周期3个月，估计一头猪苗出生后费用为400元，即p4=400（元/头），一头猪苗出售时重量大约为40kg，售价为20元/kg，一头猪苗出售时总收益为40×20=800元，即p5=800（元/头）。根据问题2，估计q=0.11（qi2+qi3）。将p1=950（元/头），p2= 2 400（元/头），p3=1 400（元/头），p4=400（元/头），p5=800（元/头），C0=5×105代入（6）式，得：

maxL=（p3-1 256）qi3+94qi2-500 00

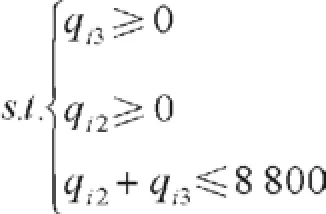
经分析发现，当p3-1 256＞94，即p3＞1 350时，qi3= 8 800，qi2=0时利润最大；当p3-1 407＜397，即p3＜1 350时，qi3=0，qi2=8 800时利润最大。

养殖场的最佳经营管理策略为：当肉猪的平均预测价格大于13.5元/kg时，养殖场在相应时间段全部出售生猪；当肉猪的平均预测价格小于13.5元/kg时，养殖场在适当时机全部出售猪苗。假设肉猪出售时的体重均为100kg，在A点附近，p3=100×19.33=1 933（元/头）；在B点附近，p3=100×17.30=1 730（元/头）；在C点附近，p3=100×14.27=1 427（元/头）；在D点附近，p3=100×17.20=1 720（元/头）；在E点附近，p3=100×15.83=1 583（元/头），即在A，B，C，D，E的附近，肉猪的平均预测价格大于13.5元/kg，当qi3=8 800，qi2= 0时利润最大，最大利润分别依次为5 457 600元，3 671 200元，1 004 800元，3 583 200元，2 377 600元；而在F点附近，p3=100×13.13=1 313（元/头），肉猪的平均预测价格小于13.5元/kg，当qi3=0，qi2=8 800时利润最大，最大利润为327 200元。三年的总利润为16 421 600元，平均每年的利润为5 473 867元。

根据以上分析，肉猪的存栏数曲线如图2所示。

由于猪肉价格下跌，利润降低，此时可以适当减少母猪的存栏数，但为了平衡生态系统，又不能下降太多，故母猪的存栏数变化很小，曲线略微向下倾斜，最大值约为1 000头，最小值约为900头。母猪的存栏数曲线如图3所示。

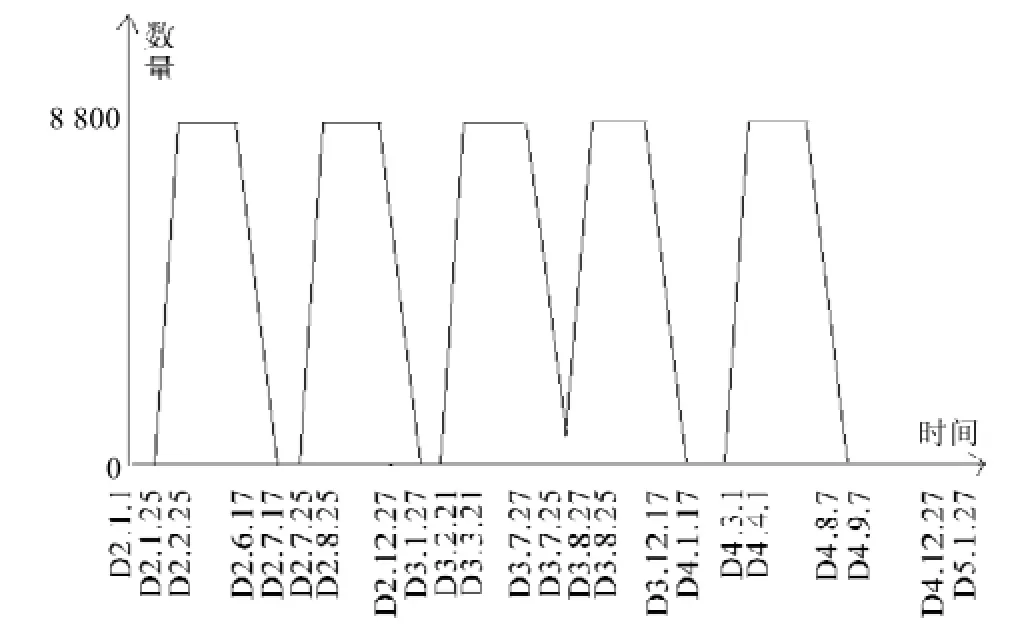
图2　肉猪的存栏数曲线

图3　母猪的存栏数曲线

4　模型的检验

4.1问题1模型的检验

模型1没有考虑种猪在怀孕、生育、哺乳等过程中由于意外、疾病等特殊原因而失去生育能力的比例，所以算出的数据比模型2略小。当种猪中母猪的比例为时，比小，所需公猪的数量较大，因而所需每头母猪每年平均产仔量略大。这些都与实际生活相符，且两个模型数据相差不大，较为合理。

4.2问题2模型的检验

模型4中的结果较模型3略大，这是由于模型4考虑乳猪在生长过程中的成活率乘以出栏率为9 2%较大引起的。因为乳猪有可能是后备种猪，因而乳猪在生长过程中的成活率乘以出栏率有可能略低于9 2%，当种猪中母猪的比例越小，节约了公猪的成本，也就减少了小猪选为种猪的比例和母猪的存栏数。总的来说，这些数据相差较小，且与实际相符。

4.3问题3模型的检验

为了追求最大利润，选取了较为理想的出售时间，此时养殖场的利润最大。另外，为了简化模型，假设成年种猪数占猪苗数与肉猪数之和的1 1%，由此固定了猪苗的出售价格，这与实际情况可能有点误差。

由于养殖场各类型猪苗的成本和出售价格受时间、地理位置等影响，且每个养殖场各类型猪苗的成本和出售价格有很大差异，所以会导致该模型存在一些误差。

5　模型的评价与推广

5.1优点

（1）所有模型都用初等方法建立，计算简单，容易理解，结果简单明确，分析具有条理性，易于决策者了解和掌握，推理过程严密、逻辑性强。

（2）所有模型都是先从具体的字母推出结论，再将调查的数据代入，求出具体的数字，采用从一般到特殊的方法，渗透了化归的数学思想方法。

（3）在问题3中，先找到生猪最佳出售时间点，再将一天的时间扩大到一个月的时间段，体现了推广的思想方法。

（4）对于问题1和问题2，各建立了两个模型，便于比较、评价，从而改进模型。

（5）对于问题3，对数据从理论上进行分析，从图形上分析出栏时间，考虑了种猪的实际因素，将理性与感性相结合，体现了数学建模的科学合理性。

（6）从所建立的模型看，更好地运用了数形结合的思想，图文并茂，使得问题更加清晰直观、形象，易于理解。

（7）所建立的数学模型与实际紧密联系，结合实际情况对所给出的问题进行求解，使模型更贴近实际。5.2缺点

模型的假设使问题过于简化。由于时间仓促，调查的数据有一定误差，模型有待进一步优化。

5.3推广

模型不仅适用于生猪养殖场，而且适用于其他养殖业，如养牛场、养鸡场、养鱼场等一系列养殖场，同时也可以给其他蔬果种植的种植场经营管理者提供借鉴。

［1］郭欣红，姜晓艳.经济数学［M］.北京：人民邮电出版社，2010：11-12.

［2］方立华.旌德县病死猪无害化处理补贴政策实施现状与对策［J］.基层农技推广，2015（1）：169-169，172.

［3］龚兰芳，韦纯勇.规模养殖场经济效益调查报告［J］.当代畜牧，2011（5）：7-8.

［4］王跃飞，郭万跃.猪人工授精技术的效益评价及实践与体会［J］.浙江畜牧兽医，2014（6）：29-30.

［5］姜启源，谢金星，叶俊.数学模型［M］.北京：高等教育出版社，1987：82-83.

［责任编辑：宣明］

Management Strategy of Pig Farms

CHENG Baojuan
（Institute of Technology， Xianning Vocational Technical College， Xianning， 437100， China）

Based on the examination question C of 2014 National College Mathematics Modeling Contest of Higher Education Cup and pig farms' operation problems， pig farms require to use their own pigs for reproduction to create the best management strategy and optimize the profits. The best management strategy is provided and an analysis is made on pig raising process in a scientific way. The linear programming model is established and the perfect management strategy is given by integrating the collected date to optimize the profit of pigs raising.

Pig raising； Breakeven point； Female pigs； Holding； Extreme point

O242.1；F326.3

A

1671-4326（2015）02-0065-06

2015-01-05

咸宁职业技术学院校级课题（2015Y006）

成宝娟（1981—），女，湖北咸宁人，咸宁职业技术学院工学院副教授，硕士研究生.