幂律流体饱和多孔介质平板通道流动特性分析

田兴旺，王平，徐士鸣

(1.大连理工大学能源与动力学院，辽宁 大连116024;2.大连海洋大学海洋与土木工程学院，辽宁大连116023)

幂律型非牛顿流体在多孔介质中的流动有着广泛而重要的工程应用背景［1-4］，如化工工程中填充塔的性能优化、资源工程中的石油热采等。由于幂律流体在多孔介质中的非达西流流动方程存在着很强的非线性效应，很难得到精确解，除了采用数值模拟方法［5-8］外，有学者借助积分的近似方法来求解［9-12］。如Nakayama等［9］对幂律流体饱和多孔介质的强迫对流问题进行了研究，运用边界层动量积分方法求解了Darcy-Brinkman-Forchheimer流动模型的动量主控方程，但积分采用了简单的线性速度分布模型。在文献［9］基础上，Nield等［10］采用同样积分方法进一步研究了常壁温条件下两平板构成的幂律流体饱和多孔介质通道内强迫对流的热发展情况。Chen等［11］通过边界层动量积分方法研究了幂律流体在多孔介质通道中的强迫对流换热过程，与文献［9］不同的是积分采用抛物线速度分布模型，得到了含有无限级数的边界层厚度的隐式表达式，但求解过程较复杂。而Thayalan等［12］也采用边界层抛物线速度分布模型，运用边界层动量积分方法，对流动充分发展的幂律流体动量主控方程进行求解，得到了边界层厚度的显式表达式及压力梯度的表达式，但没有考虑非达西流区的惯性效应。

综上，本文在前人研究的基础上，采用应用更广泛的Darcy-Brinkman-Forchheimer流动模型，通过比较边界层内线性和抛物线2种速度分布经验关系式，运用边界层动量积分方法更全面的分析了幂律流体饱和多孔介质通道的流动特性问题。得到了边界层厚度显式表达式及轴向速度和压力降的无量纲表达式，并进一步讨论了一些重要的无量纲参数，如粘性比、达西数、综合惯性参数、孔隙率等对不同流变指数流体流动速度分布及压力降的影响。

1 物理数学模型

如图1所示，研究对象为一个填充各向同性多孔介质的板间距为2H的平行板通道流动问题。考虑二维流动充分发展的稳态情况，假设流体为单相、不可压缩的幂律流体，除了流体粘性外其他流体参数物性是定值。

图1 多孔介质平板通道流动模型示意图Fig.1 Schematic diagram of flow model in a parallel plate channel filled with porous media

幂律流体Darcy-Brinkman-Forchheimer流动模型的动量主控方程为

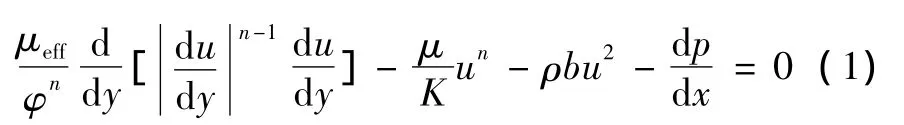
式中:u为多孔介质达西流速，m/s;μeff为幂律流体的有效稠度系数，N·s/m2;μ为幂律流体的稠度系数，N·s/m2;φ为多孔介质孔隙率，n为幂律指数，K为修正的多孔介质渗透率，mn+1;b为Forchheimer惯性系数，m－1;dp/dx为压力梯度，kg/(m2·s2)，是个定值。

定义无量纲的变量如下:无量纲坐标Y=y/H，无量纲粘度比为M=μeff/μ，特征参考速度为ud=(Kdp/(μdx))1/n，基于特征参考速度的无量纲流速为U=u/ud，基于特征参考速度修正的Forchheimer惯性参数为F=ρbK(ud)2－n/μ，修正的达西数为Da=(K/φn)2/(n+1)/H2。

把上述无量纲参数带入方程式(1)得

对应的无量纲边界条件:

按照文献［12］的分析，粘性效应被限制在贴近板壁处的薄边界层δ内，其速度梯度满足方程(2)，而边界层外为流核区，其无量纲的流核速度Uc满足方程式(4)，从而使得流动呈现结构流的特性。

对式(2)在半个通道断面上采用边界层动量积分得

相应的边界条件方程式(3)变为

对式(5)封闭求解，需要在边界层中增加一个假想的速度分布经验关系式。

假定边界层内速度线性分布，则无量纲速度分布表达式为

将速度线性分布式(7)代入到式(5)，考虑边界条件(6)，得到边界层无量纲厚度值为

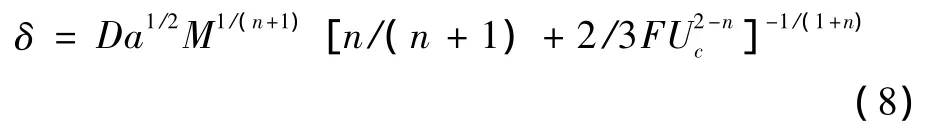
假定边界层内速度二次抛物线分布，则无量纲速度分布表达式为

把抛物线速度分布表达式(9)带入到方程(5)，考虑边界条件(6)，得到边界层无量纲厚度值为

其中，Γ为伽马函数，给定一个幂律指数n，即可求出Γ(n)。

在这里定义体积平均速度um和无量纲体积平均速度Um如下:

当把式(11)代入式(7)和(8)得

将式(11)代入式(9)、(10)得

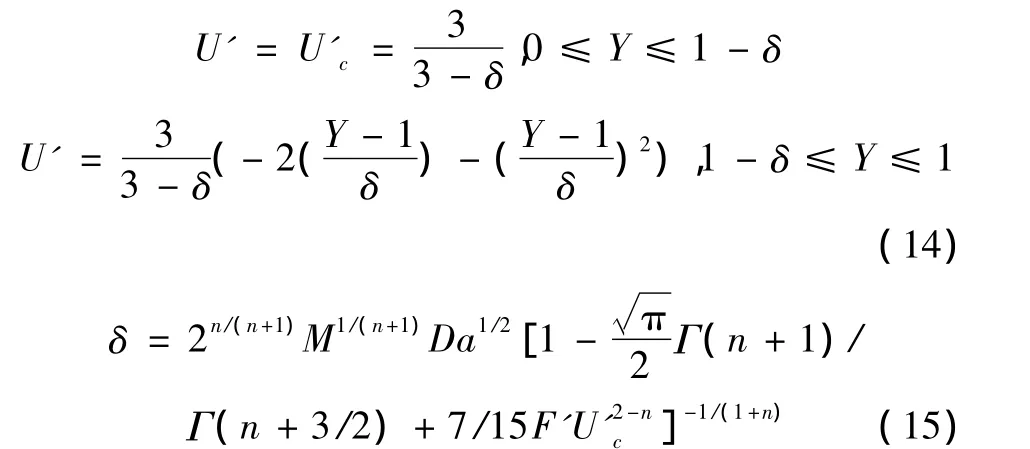
其中，F'=ρbK(um)2－n/μ ，是基于体积平均速度修正的Forchheimer惯性参数，也称为综合惯性参数，U'c是基于体积平均速度的无量纲流核速度。

根据式(1)可得到幂律型流体在多孔介质中流动的压降关系式为

定义无量纲的范宁(Fanning)摩擦系数和修正的无量纲雷诺数Re分别为

将式(17)、(18)代入到式(16)中，可得到无量纲轴向压力降方程式为

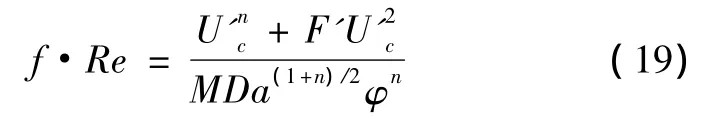
综上，已知幂律指数n、孔隙度φ，达西数Da及Forchheimer参数F'，联立式(12)、(13)或者(14)、(15)，采用迭代求解方法就能得到边界层厚度值δ和无量纲流核速度值U'c。然后代入到式(12)或(14)及(19)即可得到平板通道断面相应的流速分布曲线和压力降的具体结果。同时可以看出，边界层厚度值一方面与流体的幂律指数n和多孔介质的达西数Da密切相关，另一方面也随着流动的综合惯性参数F'的大小而变化。

对于渗透率较低的多孔介质，在流速较低时惯性效应很小，近似F'=0，此时，速度线性分布模型和抛物线分布模型所对应的边界层厚度分别为

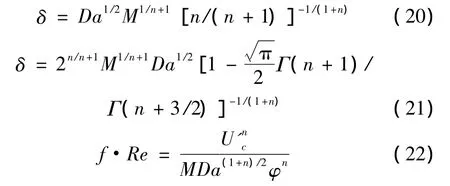
而对于渗透率较高的多孔材料，在流动惯性效应较大时，其边界层厚度和压力降与达西数Da和综合惯性参数F'均有关。

2 抛物线模型与线性模型的比较

为了证实二次抛物线速度分布和线性速度分布的有效性，将这2个模型所得的结果分别与分析解作比较。在流体为牛顿流体(n=1)、无量纲粘度比M=1和综合惯性参数F'=0的情况下，对式(2)化简得

基于特征速度和平均速度的分析解表达式分别为

图2描述了牛顿流体(n=1)在粘度比M=1、综合惯性参数F'=0时，比较了不同达西数Da情况下，抛物线和线性2种模型得出的速度分布与分析解接近程度。由图中可知，在Da较小时，抛物线和线性2种模型所对应的速度分布结果与分析解吻合度较好，这是由于较小的达西数使得边界粘性效应降低，流核区域变大，速度剖面曲线变得更平坦。这说明了在达西流区(一般可认为Da＜0.001)，边界层内假定流速分布关系式的选取对计算结果影响很小。

随着Da的增大，可以看出在边界层的邻近区域内，2种模型与分析解存在的差异也变得明显，但是抛物线模型显然比线性模型所得的速度分布结果有一个更好的近似，说明了在非达西流区，边界层内速度分布采用抛物线模型得到的结果精度较高。值得注意的是抛物线模型在本质上也更符合实际速度的分布形式，因为边界层厚度处不可能出现速度的突变。

图2 抛物线、线性模型与分析解的比较(n=1，M=1，F'=0)Fig.2 The comparison of the parabolic and linear velocity distribution models with the analysis solution for the case(n=1，M=1，F'=0)

3 计算结果分析

3.1 达西数对流动边界层厚度的影响

图3描述了在粘性比M=1及综合惯性参数F'=100的条件下，边界层厚度δ在不同幂律指数n下随达西数Da的变化情况。

图3 达西数对边界层厚度的影响(M=1，F'=100)Fig.3 The effect of the Darcy number on the boundary layer thickness for the case(M=1，F'=100)

从图3可以看出，随着达西数Da的减小，边界层厚度δ变薄，说明了边界粘性效应被限制在贴近壁面处的一薄层内。随着幂律指数n的增大，边界层厚度δ变厚，这一点不难理解，因为幂律型非牛顿流体在无多孔介质的通道内流动时，剪切变稠流体(n=1.5)比剪切变稀流体(n=0.5)的速度剖面更像抛物线。此外，从图3上还可以看出采用抛物线模型所得到的边界层厚度要比线性模型厚一些。

3.2 无量纲轴向流速分布的主要影响因素

3.2.1 达西数的影响

图4描述了在粘性比M=1及综合惯性参数F'=100的条件下，采用抛物线模型所得的无量纲轴向速度分布随达西数Da的变化情况，同时考虑幂律指数n的影响。从图4可知Da的变化对剪切变稠流体(n=1.5)的影响比剪切变稀流体(n=0.5)大，即随着Da的减小，剪切变稠流体的流核区域变化较明显，速度剖面变得平坦，壁面处边界层流动特征更加显著。这是因为多孔介质的固体基质对流体流动的阻挡作用对剪切变稠流体的影响更明显。

图4 达西数对无量纲轴向流速分布的影响(M=1，F'=100)Fig.4 The effect of the Darcy number on the dimensionless axial velocity distribution for the case(M=1，F'=100)

3.2.2 综合惯性参数的影响

图5描述了在粘性比M=1及达西数Da=0.01时，采用抛物线模型所得的无量纲轴向速度分布随F'数的变化情况，同时考虑幂律指数n的影响。从图5可知，综合惯性参数F'数的变化对剪切变稀流体(n=0.5)的影响比剪切变稠流体(n=1.5)大，即随着F'数的增大，剪切变稀流体的边界层更薄，边界层内速度梯度更大，速度剖面也变得更平坦，使得流核区域变化较明显，壁面处边界层流动特征更显著。

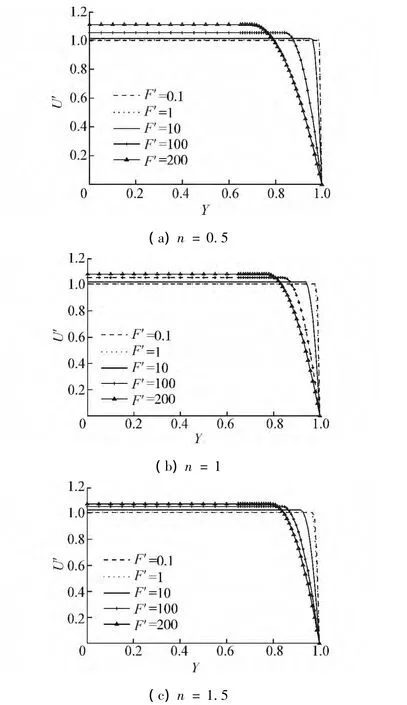
图5 综合惯性参数对无量纲轴向流速分布的影响(M=1，Da=0.01)Fig.5 The effect of the integrated inertial parameter on the dimensionless axial velocity distribution for the case(M=1，Da=0.01)

3.2.3 粘性比的影响

图6描述了在综合惯性参数F'=100及达西数Da=0.01时，采用抛物线模型所得的无量纲流核速度分布随粘性比M和幂律指数n的变化情况。由图6可知，随着M的增大，流核速度U'略微增大，但变化很小;此外，随着幂律指数n的增大，流核速度有所增加，但增加量也不大，综上可以认为无量纲粘性比对幂律型非牛顿的流核速度的影响较小，即对无量纲轴向流速分布的影响可以忽略。

图6 粘性比对无量纲轴向流速分布的影响(F'=100，Da=0.01)Fig.6 The effect of the viscosity ratio on the dimensionless axial velocity distribution for the case(F'=100，Da=0.01)

3.3 无量纲轴向压力降的主要影响因素

3.3.1 达西数和综合惯性指数的影响

图7是在M=1，φ =0.5时，幂律流体在多孔介质中流动无量纲轴向压力降随着达西数Da和综合惯性参数F'的变化关系，同时考虑了幂律指数n的影响。从图7可知，在F'数较小时，流体流动阻力趋近于Darcy流模型(F'=0)所预测出的轴向压力降方程为常数的情况;随着F'的增大，流体流动从Darcy流转变成Forchheimer惯性流，压力降迅速上升;在惯性效应较强时，压力降随综合惯性参数F'成线性增长。同时可以看出，多孔介质的特性和流体的流变特性对压力降有着较大的影响，即随着渗透率的减小(Da为0.01～0.000 1)和幂律指数n的增大，压力降也是显著增大的。

图7 达西数和综合惯性指数对无量纲轴向压力降的影响(M=1，φ =0.5)Fig.7 The effect of the Darcy number and integrated inertial parameter on the dimensionless pressure drop for the case(M=1，φ =0.5)

3.3.2 孔隙率和粘性比对无量纲轴向压力降的影响

图8是在F'=100，Da=0.01时，幂律流体在多孔介质中流动无量纲轴向压力降随着孔隙率φ和粘性比M的变化关系，同时考虑了幂律指数n的影响。从图上可知，在φ较小时，流体流动阻力很大，随着φ的增大，压力降迅速降低，但减小变缓，特别是剪切变稀流体(n=0.5)，随着φ的增大，压力降变化不明显。还可看出随着M数的增大压力降也是逐渐下降的，其中剪切变稠流体(n=1.5)较其他2种流体随着φ的增大，压力降降低更为明显。

图8 孔隙率和粘性比对无量纲轴向压力降的影响(F'=100，Da=0.01)Fig.8 The effect of the porosity and viscosity ratio on the dimensionless pressure drop for the case(F'=100，Da=0.01)

4 结论

1)推导出动量主控方程及相应边界条件的无量纲表达式，结合假定的边界层内速度分布经验关系式，得出边界层厚度显式表达式及无量纲的轴向流速和压力降的计算表达式。

2)在Da较小时，抛物线和线性2种模型所对应的速度分布结果与分析解吻合度较好，边界层内假定流速分布关系式的选取对计算结果影响很小。随着Da的增大，抛物线模型比线性模型所得的速度分布结果有一个更好的近似，边界层内速度分布采用抛物线模型得到的结果精度较高。

3)流动边界层随着达西数Da的减小而变薄，随着幂律指数n的增大而变厚;达西数Da的变化对剪切变稠流体的影响较大，而综合惯性指数F'的变化对剪切变稀流体的影响较大;无量纲粘性比M对幂律型非牛顿的流速分布的影响较小。

4)在Da较小时，流体流动阻力很大，随着Da的增大，压力降先迅速降低，但之后降低减缓;随着F'及幂律指数n的增大，流动压力降迅速上升;随着孔隙率φ和粘性比M数的增大，压力降逐渐降低。

［1］HARRIS S D，INGHAM D B，POP I.Mixed convection boundary-layer flow near the stagnation point on a vertical surface in a porous medium:Brinkman model with slip［J］.Transport in Porous Media，2009，77:267-285.

［2］CHEN H T，CHEN C K.Natural convection of a non-Newtonian fluid about a horizontal cylinder and sphere in a porous medium［J］.International Communications in Heat and Mass Transfer，1988，15:605-614.

［3］SHENOY A V.Darcy-Forchheimer natural，forced and mixed convection heat transfer in non-Newtonian power-law fluid-saturated porous media［J］.Transport in Porous Media，1993，11(3):219-241.

［4］CHENG C Y.Soret and Dufour effects on free convection boundary layers of non-Newtonian power law fluids with yield stress in porous media over a vertical plate with variable wall heat and mass fluxes［J］.International Communications in Heat and Mass Transfer，2011，38:615-619.

［5］PANTOKRATORAS A，MAGYARI E.Forced convection flow of power-law fluids over a flat plate embedded in a Darcy-Brinkman porous medium［J］.Transport in Porous Media，2010，85(1):143-155.

［6］HADIM H.Non-Darcy natural convection of a non-Newtonian fluid in a porous cavity［J］.International Communications in Heat and Mass Transfer，2006，33(10):1179-1189.

［7］CHEN G M，TSO C P.Effects of viscous dissipation on forced convective heat transfer in a channel embedded in a power-law fluid saturated porous medium［J］.International Communications in Heat and Mass Transfer，2011，38(1):57-62.

［8］EL-AMIN M F，SALAMA A，et al.A conditionally stable scheme for a transient flow of a non-newtonian fluid Saturating a porous medium［J］.Procedia Computer Science，2012，9:651-660.

［9］NAKAYAMA A，SHENOY A V.Non-Darcy forced convective heat transfer in achannel embedded in a non-Newtonian inelastic fluid-saturated porous medium［J］.Can J Chem Eng，1993，71:168-173.

［10］NIELD D A，KUZNETSOV A V.Thermally developing forced convection in a channel occupied by a porous medium saturated by a non-Newtonian fluid［J］.International Journal of Heat and Mass Transfer，2005，48(6):1214-1218.

［11］CHEN G，HADIM H A.Forced convection of a power-law fluid in a porous channel—integral solutions［J］.Journal of Porous Media，1999，2(1):59-70.

［12］THAYALAN N，HUNG Y M.Momentum integral method for forced convection in thermal nonequilibrium power-law fluid-saturated porous media［J］.Chemical Engineering Communications，2013，200(2):269-288.