船用复合材料连接结构稳定性分析方法

于福临，姚熊亮，郭君，王耀辉

(哈尔滨工程大学船舶工程学院，黑龙江哈尔滨150001)

复合材料具有可设计性强的特点，以其无法比拟的优势在航空航天、船舶工程、建筑工程、兵器工业等领域得到了应用［1］。夹层复合材料在舰船隐身设计中得到了广泛应用［2］，采用隐身设计的舰船结构除满足隐身设计要求外，还需要满足基本的强度、刚度、稳定性甚至是抗爆性能要求［3］。复合层梁的稳定性计算是结构分析的重要组成部分［4］。船舶桅杆复合材料结构设计中，为保证结构的强度，在结构的端部进行了结构的加强，厚度及材料配置与中间位置不同，使得材料性能存在长度方向上的截面的变化。对于变截面复合材料结构稳定性问题的研究主要集中在复合材料刚度计算方法和失稳临界载荷的计算［5］，但相关试验较少。针对船用复合材料连接结构在试验中出现的失稳模式，采用了传递矩阵方法对稳定性计算方法进行分析，并开展了数值仿真和模型试验，对计算方法的精度进行了验证。

1 连接结构失稳问题

1.1 模型

图1表示本文采用的船用复合层梁结构横剖面形式。表面由弹性模量较大的玻璃钢组成;芯材由密度低、弹性模量较小的泡沫组成。

船舶桅杆受力复杂，特别是复合层板结构应用到船体上时，在受到重力和风载荷、惯性力等载荷作用时，桅杆与钢质船体甲板的连接部位容易发生失稳，连接结构的稳定性会影响到桅杆整体性能，应予以重点考核。

图1 复合材料剖面图Fig.1 Sandwich composite profile

1.2 稳定性破坏模式

为了研究复合层梁结构的稳定性问题，本文开展了层梁模型稳定性试验，图2表示稳定性试验图。试验中，通过MTS系统对试验样件施加轴向载荷，至试件产生破坏停止，测量得到轴向失稳载荷。

在试验中观察到了不同的失稳模式，图3和图4给出了船用复合层梁结构整体和局部失稳试验图。

图2 稳定性试验布置图Fig.2 Stability experimental set-up

图3 复合层梁整体失稳模式图Fig.3 Mode of composite laminates overall instability

图4 复合层梁局部失稳模式图Fig.4 Mode of composite laminates local instability

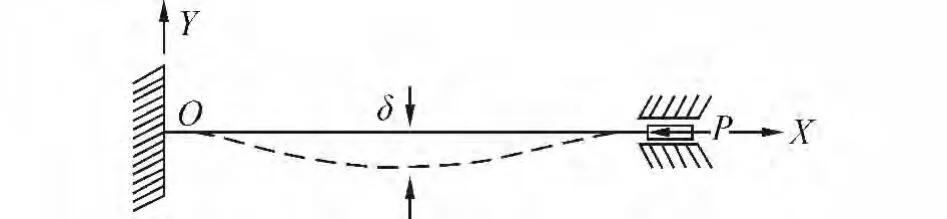
图5 力学模型Fig.5 Mechanical model

图5给出了船用复合材料连接结构稳定性分析力学模型。通过试验发现了复合层梁结构的稳定性破坏模式，但是没有适用于船用复合材料连接结构的稳定性计算方法，本文基于试验中发现的问题，开展了稳定性计算方法研究，提出了基于刚度等效和传递矩阵方法的稳定性计算方法。

2 等效刚度计算

2.1 等效弯曲刚度计算

假设在外载作用下，复合材料的各夹层应变相等，各层都为匀质材料。等效弯曲刚度采用下式进行计算［8］:

等效弯曲刚度表示为

式中:i表示夹层，n表示层数，Ei表示第i层材料的弹性模量，Ii表示第i层材料相对于中和轴的惯性矩。

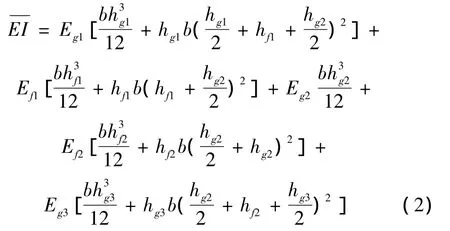
式中:hg1、hg2、hg3为各玻璃钢夹层厚度，其中hg1=hg2;hf1、hf2为泡沫芯材厚度，其中hf1=hf2。

2.2 等效剪切刚度计算

针对船用复合层梁结构，等效剪切刚度设为，其中为船用复合材料的等效剪切模量［9-10］。

等效剪切刚度可用下式计算:

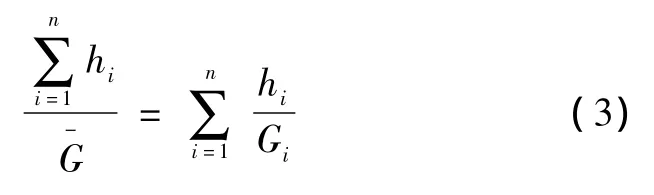
式中:i表示夹层，n表示层数，hi表示第i层材料的厚度，Gi表示第i层材料的剪切刚度。

船用复合层梁的夹层结构形式导致了横剖面应力分布不均匀，应用能量法修正复合层梁截面的剪切应力。复合层梁结构如图1，其中hg1=hg2=hg3=h，hf1=hf2=h*，剪切应变能如下式:

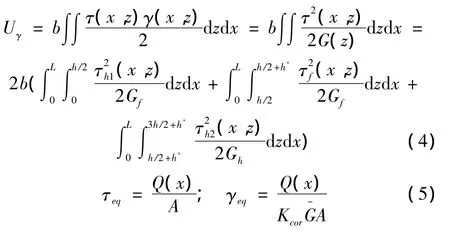
式中:τeq表示等效剪切应力，γeq表示等效剪切应变，Kcor表示修正系数，A表示截面积，Q(x)表示剪力。

则剪切应变能Uγ为

对于矩形截面剪应力有

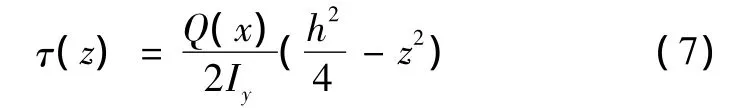
根据弹性模量的不同，重构剪应力分布［6］，对船用复合层梁结构剪应力进行计算并带入式(4)可得

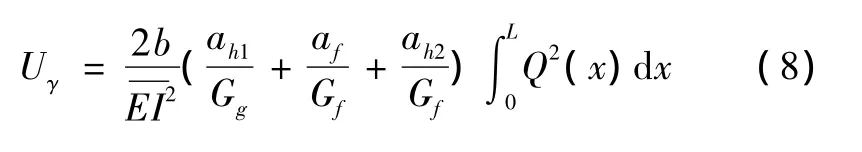
其中

由式(13)和式(14)可得剪切修正系数的表达式为

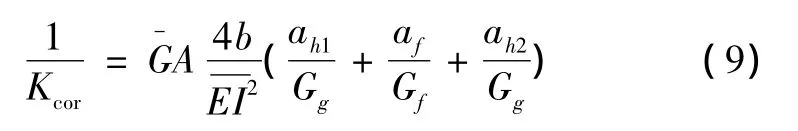
式(9)中，当h=0时或h*=0，Kcor=5/6，说明剪切修正方法是正确的［7］。本文采用的船用复合层梁结构的剪切修正系数为:Kcor=1。

3 基于传递矩阵法的复合层梁稳定性计算方法

基于Timoshenko梁理论，应用传递矩阵法，对复合层梁结构的稳定性进行求解。对于存在功能梯度的复合层梁的屈曲载荷计算中，采用无长度无质量的转动弹簧模型对刚度变化进行等效分析［11-12］。

截面上任一点位移:

正应变、剪应变为

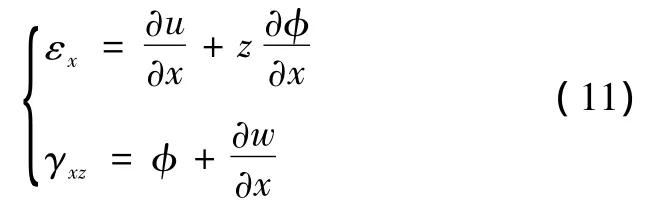
轴向力T、弯矩M、剪力Q分别为

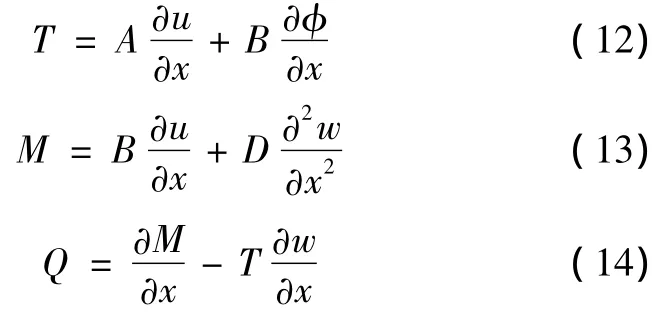
一阶剪切模型控制方程:

由式(15)可得

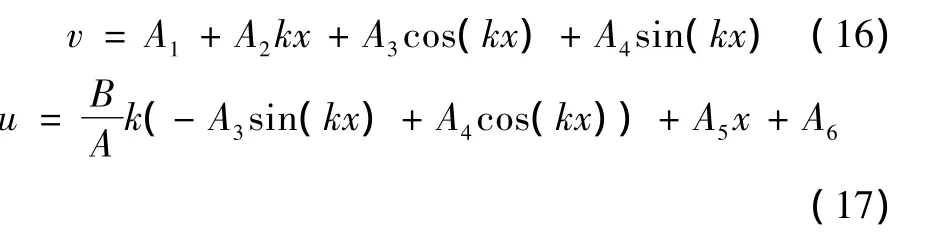
将上式代入式(12)～(14)中得

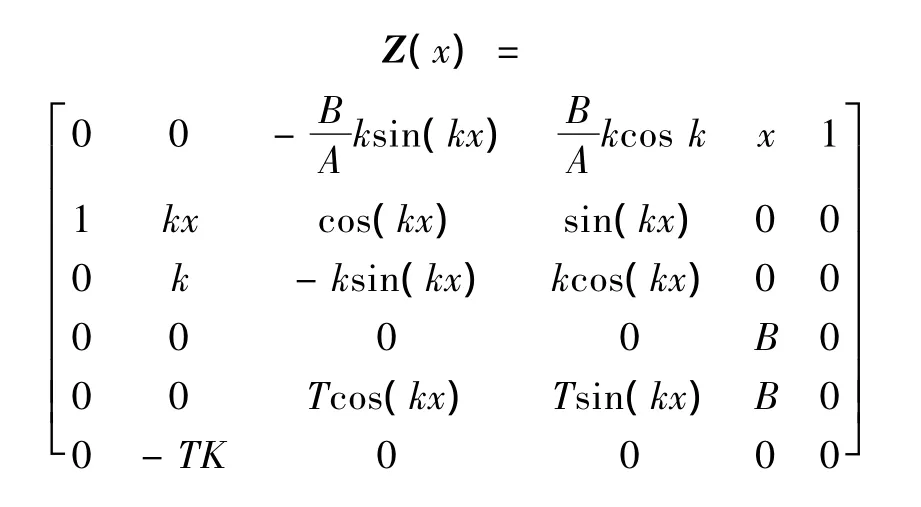
将复合层梁离散成n个分段，对于第i个分段，左端面位置为xi1，右端面为xi2。

可以得到传递矩阵:

对于变截面的复合层梁，认为不同离散分段之间位移、轴向力和弯矩连续，而转角存在间断［12］。

式中:k*表示刚度系数，φi+1为i+1段的转角，φi为第i段的转角。

不同分段相邻截面之间的变量关系为

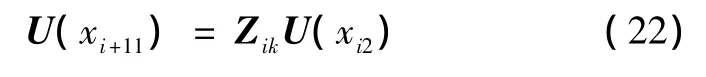
式中:

将式(19)代入式(22)可得

可以得到求解复合层梁结构稳定性的传递矩阵方程为

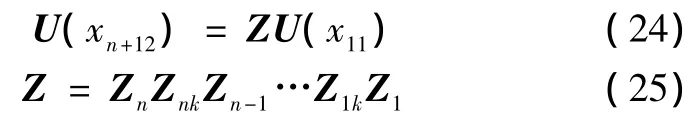
对于一端固支，一端自由的复合层梁，根据边界条件可得特征值计算式为

对于特征值的求解，可以得到一端固支、一端自由的复合层梁的临界载荷值Pcr。

相对于能量法等理论求解方法，传递矩阵方法易于编程，程序化程度高，对于处理功能梯度材料具有更好的通用性，而且计算效率更高。

4 稳定性计算分析

4.1 计算结果与数值计算结果对比

对计算结果进行无量纲化处理，屈曲载荷为crfem，Pcr为FEM和TMM计算得到的屈曲载荷，Pcrfem为FEM得到的屈曲载荷。

TMM表示传递矩阵方法，FEM表示有限元方法，从表1与有限元方法的计算结果对比可以看出，传递矩阵方法精度较高。

表1 计算结果比较Table 1 Comparison between TMM and FEM values

4.2 理论计算结果与试验结果对比

对计算结果进行无量纲化处理，屈曲载荷为crtmm，Pcr为试验和TMM得到的屈曲载荷，Pcrttmm为TMM得到的屈曲载荷。

根据1.2节中试验，对三组试验试件进行加载试验，传递矩阵法计算值与试验值比较见表2。考虑样件的离散性，对试验值取平均，将传递矩阵法计算结果与试验值进行对比，平均误差为10.74%，可以看出传递矩阵方法计算精度较高，误差产生的原因可能是本文提出的方法对挠曲线的描述与实际并不完全一致，并且复合材料试件存在一定的离散性，导致计算结果与试验产生了一定的误差。

本文提出的稳定性分析方法可以对整体失稳模式进行计算分析，局部分层失稳是由于面内剪力和层间剪力引起的，对于复合层梁局部失稳还无法进行分析，还需对方法进一步改进。

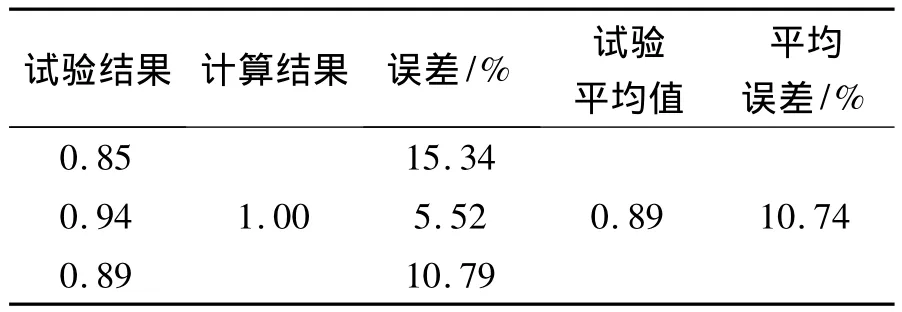
表2 传递矩阵方法计算值与试验值结果比较Table 2 Comparison between TMM and experimental values

5 结论

本文对船用复合材料与钢质船体结构连接部位的失稳进行分析，基于传递矩阵方法，提出了连接部位复合层梁结构的稳定性理论计算方法。

1)开展了复合材料连接结构失稳破坏模式试验，发现了整体失稳和局部失稳的失稳模式。

2)根据船用复合层梁的结构形式，对其进行了等效弯曲刚度计算和等效剪切刚度计算，计算并验证了剪切修正系数。

3)采用传递矩阵方法对复合层梁结构的稳定性进行了分析，并与试验结果进行了对比，计算方法精度较高，对上层建筑与钢质船体结构连接结构的设计和制造提供了工程设计参考。

［1］刘敬喜，谭安全，李天匀，等.复合材料层合圆柱壳中振动功率流特性［J］.哈尔滨工程大学学报，2012，33(3):269-274.LIU Jingxi，TAN Anquan，LI Tianyun，et al.Characteristics of the vibration power flow in a laminated composite cylindrical shell［J］.Journal of Harbin Engineering University，2012，33(3):269-274.

［2］MOURITZ A P，GELLERT E，BURCHILL P，et al.Review of advanced composite structures for naval ships and submarines［J］.Composite Structure，2011，53:21-41.

［3］HELLER S R.The use of composite materials in naval ships［M］.Oxford:Pergamon Press，1967:69-111.

［4］王颖坚.复合材料层合板的稳定性分析［J］.北京大学学报:自然科学版，1989，1(7):75-89.WANG Yingjian.Stability analysis of composite laminates［J］.Acta Scientiarum Naturalium Universitatis Pekinensis，1989，1(7):75-89.

［5］RAHAI A R，KAZEMI S.Buckling analysis of non-prismatic columns based on modified vibration modes［J］.Communications in Nonlinear Science and Numerical Simulation，2008，13:1721-1735.

［6］ATTARD M M.Global bucking experiment on sandwich columns with soft shear cores［J］.Electronic Journal of Structural Engineering，2011，11(1):21-31.

［7］JENSEN C.Defects in FRP panels and their influence on compressive strength［D］.Lyngby:Technical University of Denmark，2006:90-95.

［8］SURESH S，MORTENSEN A.功能梯度材料基础制备及热机械行为［M］.李守新，译.北京:国防工业出版社，2000:130-150.

［9］Huang H，Kardomateas A G.Buckling and initial post buckling behavior of sandwich beams including transverse shear［J］.AIAA Journal，2002，40(11):2331-2335.

［10］王耀辉.船舶桅杆复合层板结构稳定性计算方法研究［D］.哈尔滨:哈尔滨工程大学，2013:71-72.WANG Yaohui.Research on the calculation method of composite laminate structure stability for ship mast［D］.Harbin:Harbin Engineering University，2013:71-72.

［11］WANG Q，QUSK S T.Repair of cracked column under axially compressive load via piezoelectric patch［J］.Computers＆ Structures，2005，83(15):1355-1363.

［12］魏东，刘应华.含裂纹功能梯度 Euler-Bernoulli梁和Timoshenko梁的屈曲载荷计算与分析［J］.复合材料学报，2010(4):124-130.WEI Dong，LIU Yinghua.Buckling of functionally traded Euler-Bernoulli and Timoshenko beams with edge cracks［J］.Acra Material Composite Sinica，2010(4):124-130.