基于单位弧长增量插补法的参数曲线电火花线切割插补方法研究

陈　昊，陈　默，奚学程，赵万生

（上海交通大学机械与动力工程学院/机械系统与振动国家重点实验室，上海200240）

基于单位弧长增量插补法的参数曲线电火花线切割插补方法研究

陈昊，陈默，奚学程，赵万生

（上海交通大学机械与动力工程学院/机械系统与振动国家重点实验室，上海200240）

对电火花线切割中基于单位弧长增量法的参数曲线插补方法进行了研究。在该方法中，各坐标轴被看作弧长参数的函数。在每个插补周期中，插补参考点沿着曲线前进一个单位弧长，并将所产生的各个进给轴的增量分别送至其累加器。某个轴的累加器每溢出一次，该进给轴输出一个增量脉冲。从参数曲线的参数方程结构出发，通过使用单位弧长增量插补法，可实现渐开线、摆线、阿基米德螺线、抛物线等参数曲线的直接插补。通过对上下异形面中较短的曲线进行再参数化，将弧长参数统一，实现了对上下异形面的四轴联动直接插补。

参数曲线；单位弧长增量插补法；插补算法

电火花线切割加工在模具制造领域有着至关重要的作用，也更多地被运用于直接加工零件中［1］。在一些典型零件（如冲压模具、飞行器模型、汽车模具等）的轮廓表达上常采用参数曲线的方式［2］。参数曲线可采用数控机床进行加工，而大部分数控机床在处理参数曲线的插补问题时采用传统的数据采样法（SDM）［3］，其原理是将这些曲线分成很多的小曲线段，然后用小曲线段的弦线替代小曲线段，相当于用大量的小直线段代替一条曲线。这种处理方式会产生一个弓高误差，并会造成曲线切线方向的速度不连续。同时，电火花线切割特有的针对上下异形面的变锥度加工功能也在工件形状不断复杂化的情况下越来越重要。其难点主要在于如何协同规划上下两个平面曲线的插补，在保证一定加工精度的条件下稳定地进行电火花线切割加工。

面对上述问题，国内外学者进行了一些相关的研究。但由于受SDM自身原理的限制，如果想要保证较高的加工精度和较均匀的进给速度，则需CAM系统生成大量的数控加工代码，在SDM的任何方法中，随着采样间隔的增大，必然会增大误差。另一种避免大量加工代码的方法就是在插补过程中利用SDM实时地对曲线进行插补，生成小的线段［4］。近期的主要研究集中在基于SDM减少速度波动和减小轮廓误差方面，并未对新的方法进行探索，如：文献［5］对这一过程增加了前瞻速度的规划来减少速度波动，但需大量的存储空间。而现有的部分以采用脉冲增量法（如逐点比较法、数字积分法、最小偏差法等）为基础的局限性在于：对于圆弧的插补需进行过象限的判别；沿曲线的插补进给速度不均匀，从而导致对上下异形面插补的精确等比例控制过程变得困难和复杂。

因此，文献［6］在基于数字积分法的思想上，提出了单位弧长增量插补法，并将其运用于线切割上下异形面的插补中；同时，对非圆参数曲线的插补进行了相关研究，实现了单位弧长增量插补法在非圆参数曲线上的运用。该方法能使插补一条曲线的过程中保持切线方向上的速度恒定，且只需一条插补指令。本文主要介绍基于单位弧长增量插补法的参数曲线加工方法在电火花线切割上的运用。

1　参数曲线的单位弧长增量插补法原理

由于电火花线切割加工需同时考虑正反向的插补，故在其应用中，脉冲增量插补法比数据采样插补法更普遍。单位弧长增量插补法就属于脉冲增量插补法的范畴，可适用于n维空间。为便于讨论，先从n=2维空间开始讨论。

一条曲线的参数方程可表示为其累积弧长的函数：

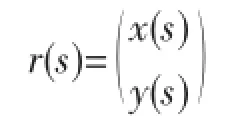
为便于对算法进行统一描述，以x1代替x、x2代替y来表示曲线坐标。在单位弧长增量插补法的每个周期中，插补点沿着参数曲线前进1个机床脉冲当量（BLU，Basic Length Unit），可用s表示弧长参数，每个进给轴的增量可用它们的m阶泰勒展开式来表示：

m一般可根据参数曲线的类型进行选择。经验证，在多数情况下，m=1或m=2时即可满足精度要求。

为便于实现算法的编程，不同阶的泰勒展开可分开表示：

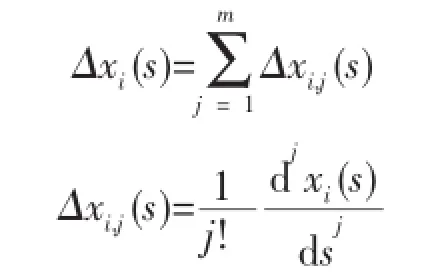
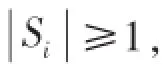
例如：在一个插补周期中，选取m=2的情况，各个轴的累加器会先根据泰勒展开式进行更新：

Si的值会被保留到下一插补周期。

图1是一个周期中的插补过程。每一个曲线都被同等地看做一条“广义上的直线”，插补的过程就像是一个点沿着“广义上的直线”在前进。当点前进1个BLU时，累加器计算的过程实质上是在找距离该点最近的网格上的交叉点。

图1　广义单位弧长增量插补法示意

单位弧长增量插补法的终点判别方法是根据所需插补曲线的总长度进行的，在插补的一开始，插补参数曲线的总长度由软件模型给出。

对于许多非圆参数曲线来说，可通过其参数方程计算得到：

用微分形式可表示为：

微分形式可通过式（3）和弧长参数s联系起来：

由此可见，在插补过程中，从参数曲线方程的结构出发，将参数曲线的微分形式与弧长参数建立联系，可得到泰勒展开式的运算结果，进而实现参数曲线的插补。通过该原理可实现渐开线、阿基米德螺线和摆线的直接插补，其插补的计算机仿真结果显示，通过采用单位弧长增量插补法得到的曲线与理想曲线基本重合（图2）。

图2　插补图形仿真

对于一些非圆参数曲线来说，参数方程中不包含参数t，故其处理方法会有所不同。抛物线是一种轴对称曲线，一个开口向上的抛物线的参数方程可表示为：

式中：p为抛物线的焦距。其参数方程能与弧长参数通过式（5）进行联系：

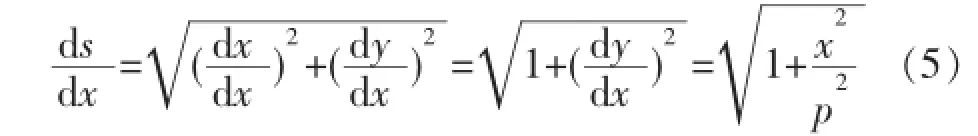
从而得到：

由此可见，尽管参数方程的类型有所不同，但同样可采用单位弧长增量插补法对参数曲线进行插补，并可看出该方法能在不进行线性近似的情况下，通过一条指令直接对曲线插补。在插补过程中，每个周期沿切线方向增加1 BLU的距离，所以只需保证插补周期相等，就能得到恒定的进给速度。如果在插补过程中，按需求合理规划插补周期，就能实现进给速度的控制。

对于上下异形面零件，在处理上、下平面加工路径曲线同时插补的问题上，主要是解决弧长参数的统一化。以（x1，x2）表示下平面曲线的坐标（X，Y）、（x3，x4）表示上平面曲线的坐标（U，V），则上、下平面曲线的弧长参数表达式为：

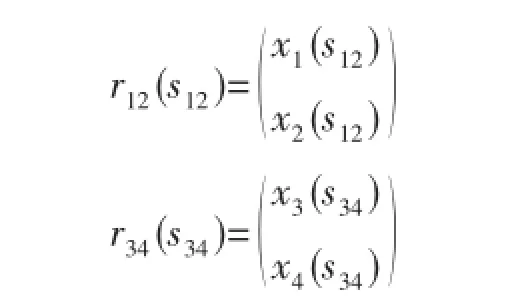
为了同时开始插补，并同时结束插补，两条曲线必须保证弧长上的线性比例关系：

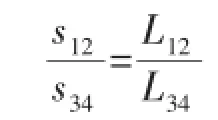
选取两个弧长中较长的一个作为广义弧长参数，设为L，并对上、下平面曲线做参数变换，可得：

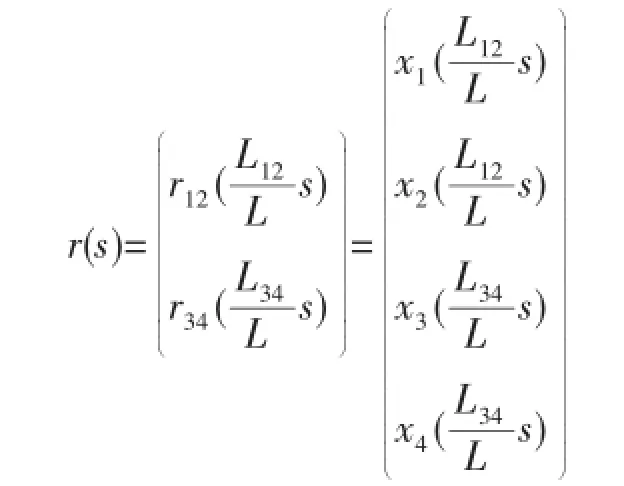
通过简单的线性变化，可在单位弧长增量插补法的基础上，将两条曲线统一为一条曲线，有效地一步插补上下异形面的两条曲线。

2　仿真实验

以渐开线插补为例，选取渐开线中心点（0，0），1 BLU选取为高精度机床常用的0.1 μm，取0～π/2这一段进行仿真，工件形状见图3。数据采样法的G代码采用UG NX 7.0生成，最大允许误差为CAM所允许的最大弓高误差，实际插补的误差会因插补网格与小线段之间存在精插补误差而更大。

图3　渐开线工件模型

利用泰勒展开至一阶，渐开线的参数方程为：

选取R为10 mm，数据采样法选取的最大弓高误差分别为1 μm（10 BLUs）和0.3 μm（3 BLUs），其平均误差由于是由CAM生成，故并未计算。实验结果见表1。可看出，单位弧长增量插补法的精度已达到一个很高的水平。在加工一个基圆直径为10 mm的渐开线时，其最大误差仅为0.4 μm，误差绝对值平均后更是＜0.3 μm。如果想用数据采样法得到同等精度的结果，就需几百条G代码，这就是数据采样法进行了线性近似所造成的结果。

表1　仿真数据结果

此外，若将尺度再放大10倍，基圆直径调整为100 mm，可得最大误差为5.382 588 μm、平均误差为3.577 758 μm，最大误差和平均误差分别只增加了26.8%和32.0%。由此可见，单位弧长增量插补法对于尺度并不是特别敏感。

本课题组曾以经典的“天圆地方”形状工件为例，进行了仿真分析和加工实验（图4）［7］。工件一共只需4条指令便可加工而成，每条指令同步插补四分之一圆和一条线段的直纹面。同时，本方法在插补上下异形面时并不仅限于圆弧和直线，对于其他参数曲线也能统一化处理。

图4　单位弧长增量插补法插补“天圆地方”工件

3　结论

本文介绍了单位弧长增量插补法的基本原理及其在参数曲线插补上的运用，还介绍了渐开线、阿基米德螺线、摆线和抛物线等非圆参数曲线的插补原理，并进一步介绍了采用单位弧长增量插补法处理四轴联动上下异形面的方法。通过仿真验证了单位弧长增量插补法的灵活性，其优势在于：

（1）能一步直接插补非圆参数曲线，如渐开线、阿基米德螺线、摆线和抛物线等；而数据采样法需对曲线进行线性近似，并将其处理成大量小线段。

（2）避免了采用小直线段逼近原始曲线所带来的弦高误差，可得到很好的插补精度；而数据采样法在保证精度的前提下需大量的指令，造成了速度损失。

（3）只需一条指令便可插补一条曲线，简化了CAM过程，使数据采样法所需的精插补和粗插补两步简化为一步。

（4）可在上下异形面的处理上自动保持上下异形面间的线性等比例速度插补关系。

（5）可保持插补过程中切线方向上的匀速，并通过对插补周期的速度规划，实现进给速度的策略控制；而数据采样法需进行前瞻的速度规划来减少速度波动。

由单位弧长增量插补法的原理可见，该方法不但可用于电火花线切割加工，也可用于通用CNC机床和带旋转轴的多轴联动机床。

［1］ Yang M Y，Park J H.A study on an open architecture CNC system with a NURBS interpolator for WEDM［J］. The International Journal of Advanced Manufacturing Technology，2002，19（9）：664-668.

［2］ Yeh S S，Hsu P L.Adaptive-feedrate interpolation for parametric curves with a confined chord error［J］.Computer-Aided Design，2002，34（3）：229-237.

［3］ Suh S，Kang S，Chung D.Theory and Design of CNC Systems［M］.London：Springer，2008.

［4］ Jeong S Y，Choi Y J，Park P.Parametric interpolation using sampled data［J］.Computer Aided Design，2006，38：39-47.

［5］ Dong Haitao，Chen Bing，Chen Youping，et al.An accurate NURBS curve interpolation algorithm with short spline interpolation capacity［J］.The International Journal of Advanced Manufacturing Technology，2012，63（9-12）：1257-1270.

［6］ 陈默，陈昊，赵万生.电火花线切割机床四轴联动单位弧长增量插补法［C］//第15届全国特种加工学术会议论文集（上）.南京，2013：259-265.

［7］ Zhao Wansheng，Chen Mo，Chen Hao.A novel trajectory interpolation algorithm for WEDM-unit generalized arc length increment method［J］.Procedia CIRP，2013，6：256-261.

Research on Parametric Curve Interpolation for WEDM Based on Unit Arc Increment Method

Chen Hao，Chen Mo，Xi Xuecheng，Zhao Wansheng
（School of Mechanical Engineering，Shanghai Jiao Tong University/State Key Laboratory of Mechanical System and Vibration，Shanghai 200240，China）

A parametric curve interpolation algorithm for WEDM which is based on unit arc length increment method is proposed.Each coordinate axes are treated as the functions of arc length.In each interpolation period，the interpolation reference point moves 1 unit arc length along the curve and the corresponding increments of each axis are accumulated.Once the accumulator of an axis exceeds，it will move 1 basic length unit.The interpolations of involute，cycloid，Archimedes spiral，parabola are achieved by using this interpolation method which starts from parametric curve interpolation structure. The ruled surfaces which are described by two curves in the upper and lower planes of a workpiece can be directly interpolated by taking re-parameterization of the shorter curve to unify the arc length parameter.

parametric curve；unit arc length increment method；interpolation algorithm

TG661

A

1009－279X（2015）04－0025-04

2015-03-31

国家自然科学基金资助项目（51175337）；国家科技重大专项（2014ZX04001061）；机械系统与振动国家重点实验室项目（MSVMS201111）

陈昊，男，1989年生，博士研究生。