基于遗传/模拟退火算法考虑压降的换热网络优化改造

吴敏，肖武，贺高红

（大连理工大学精细化工国家重点实验室膜科学与技术研究开发中心，辽宁 大连 116024）

在过去的四十年里，换热网络综合一直是过程系统工程重要的研究领域之一，而且已经取得了许多研究成果。很多研究成果都已经可直接应用于实际工厂并实现工艺物流间的能量回收最大化、公用工程用量和换热面积的最小化。Björk和 Nordman[1]认为相当多的学术研究都集中于新工厂换热网络的集成，但是忽略了现存换热网络通过改造往往会获得更大的节能潜力。由于新建工业项目逐渐减少且工业生产的利润空间越来越小，通过改造现存工厂的换热网络来实现节省操作费用的目的是刺激换热网络改造研究不断发展的契机。换热网络的结构是否最优，往往与能源价格、换热器的经济参数直接相关，且国内外的过程工业现有的换热网络大多都是几十年前设计的，当时的经济条件以及制造工艺与现在差异较大、操作条件也发生了很大的变化。据估计，全球范围内有70%～80%的换热网络需要改造[2]。

1984年，Linnhoff和Vredeveld[3]首先提出了换热网络改造的概念。随后Westerberg[4]以及Briones[5]等对换热网络改造问题进行了系统的研究，认为换热网络改造的难度要远远大于换热网络的基础设计。在换热网络的改造过程中，不仅要考虑原有换热器的再次利用，还需要考虑新换热单元的匹配。

换热网络改造的文献主要分两种：第一，基于热力学原理的夹点改造法[6]；第二，基于数学规划法的纯数学优化改造法[7]。

基于夹点技术的换热网络改造方法最早由Tjoe和Linnhoff[6]提出，主要的改造方式是通过增加现有换热面积来减少公用工程的消耗，但是没有考虑换热设备的重新匹配。基于数学规划法的换热网络改造策略最早由Ciric和Floudas[7]提出，采用的是一种分解改造策略：第一步，以最小年总费用为目标，基于转运模型的MILP优化流股的匹配；第二步，建立一个NLP模型来优化第一步所提出的匹配方案，得出最后的改造的换热结构。但是，这种方法的缺陷在于MILP数学模型无法准确地计算换热面积，而且大量的整数变量使得无法运用于工业规模的问题。随后Ciric[8]以及Yee[9]等首先基于超结构建立了MINLP数学模型用于解决换热网络改造，但是仍然沿用了等温混合的假设；Zhu等[10]将夹点法与数学规划法结合到一起，并提出了一种网络夹点的观点，网络夹点的定义是因违背了最小传热温差约束而引起传热瓶颈的换热器。Bagajewicz等[11]对一个原油预热系统进行改造，分别运用夹点分析法和数学规划法对该系统进行研究，最后得出了结论：分三步（目标阶段，设计阶段，调优阶段）进行的换热网络改造结果不论是在经济性还是可行性上都不如基于转运模型的数学规划法。Pan等[12]通过对换热器的详细设计实现了换热网络的改造，且实现了更大的能量回收。Sreepathi等[13]研究了多种现有换热器的重排策略来研究换热网络改造，并将其中一种最优策略应用到一个多目标优化问题。

Bjork等[14]对比了非等温混合和等混混合方式的换热网络超结构，将这两种模型应用于同一个算例，最终的年总费用大约会有10%左右的差别，证明数学模型中如果有过多的不合理假设将会导致较大的差异。文献[15-18]以非等温混合分级超结构为基础，对换热网络同步综合和优化改造进行了广泛的研究。

本文所提出的换热网络改造数学模型就是在非等温混合超结构的基础上建立的，同时考虑了原有换热设备的重新配置、现存换热器面积的增加、新换热设备的购置、新增动力设备。由于GA/SA（遗传/模拟退火）算法可有效避免局部最优解且解决NLP数学问题的性能较好，最后用GA/SA算法求解所提出的数学模型。

1 数学模型

换热网络的优化改造往往需要对现有换热设备进行重新配置来增大热回收能力，但是如果重新配置之后现有的换热面积依然无法达到所设定的目标回收量，那么就需要通过对现有的换热器增加管束来增大换热面积或者新增换热设备来弥补。传热面积的增加使所形成的压力降肯定会超出现有泵所能提供的压头，此时就需要购置大功率的动力设备，然而这些设备往往是很昂贵的。如果购置泵的费用大于所节省公用工程等的费用，将会得出不合理的改造方案，所以在换热网络的改造中同时优化压降是很有必要的。

换热网络的优化改造需要主要解决的问题如下所述。

（1）现存的换热单元热负荷重新分配，以及参与改造的工艺物流新匹配结构的变化。

（2）判断某一匹配是否选用原有的换热器，或者使用其他匹配位置的换热器，或者使用新增的换热器。

（3）计算新增换热单元的面积。

（4）计算原有换热器中需要新增加的面积。

（5）换热网络结构发生变化，重新匹配原有设备的费用。

（6）改造后的换热网络压力降增大，原有动力设备提供压头不足，需要新增动力设备。

以上6项任务之间彼此并不独立，内部存在相互关联性。例如，确定各换热单元的面积必须先确定换热网络的整体结构，未确定每一匹配的传热面积之前不能确定出换热器的匹配分布。改造的费用主要包含以下两个方面：新增换热器和换热面积增加的费用，新增动力设备的费用。考虑压降的换热网络分级超结构如图1所示，对于该模型的具体描述可参考文献[1]。

1.1 约束条件

（1）每条流股的热平衡约束

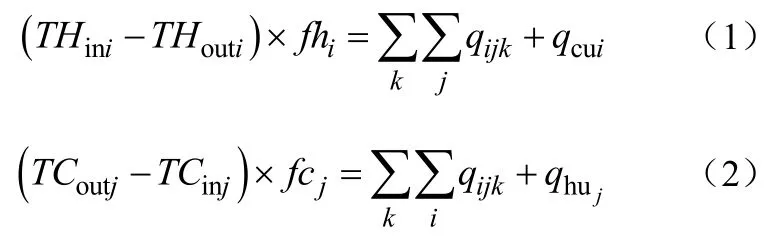
（2）每个换热器的热平衡约束

（3）第k级各分流流股的质量、能量衡算 热流股：

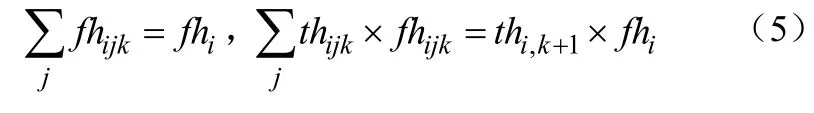
冷流股：

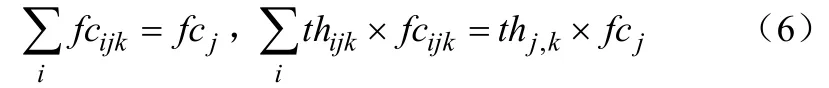
（4）各物流的入口温度

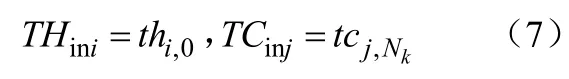
（5）可行性温度约束

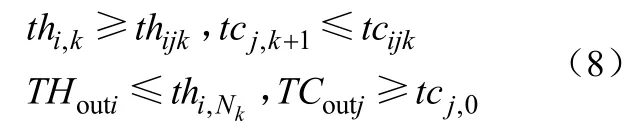
（6）冷热公用工程负荷

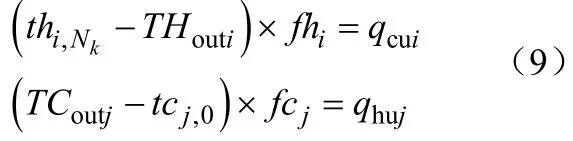
（7）最小传热温差约束

对换热器：

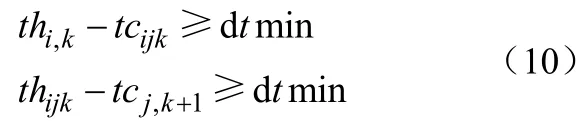
对热公用工程：

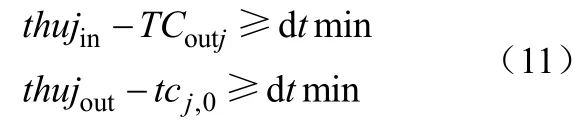
对冷公用工程：

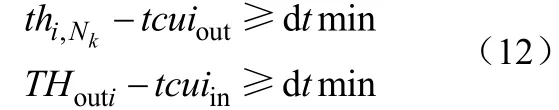
式中，thujin与thujout分别表示热公用工程的进出口温度，tcuiin与tcuiout分别表示冷公用工程的进出口温度，dtmin表示允许的最小传热温差。

图1 考虑压降超结构简图

（8）压降约束

（9）新增动力约束

（10）其他约束

以下表示对于现有换热器的新增面积和新增换热器的约束条件

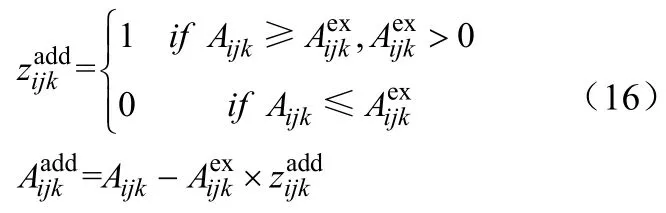
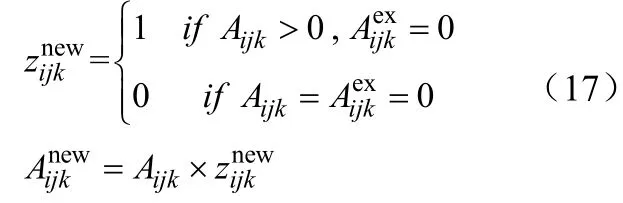
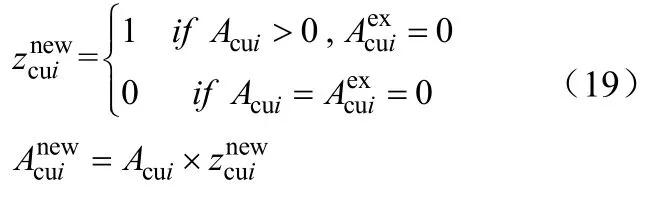
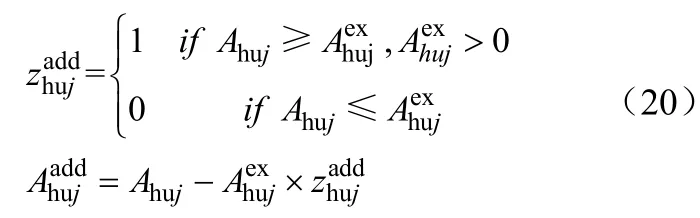
1.2 目标函数

Mincost表示换热网络最小的改造费用，目标函数包括三个部分：Cutility表示改造后换热网络公用工程费用，Carea表示改造所需的换热面积投资费用，Cp/c表示改造后需要增加的动力费用。

2 GA/SA算法求解思路

遗传算法（GA）[19]和模拟退火算法（SA）[20]是目前解决全局优化比较有用的方法。遗传/模拟退火算法的基本思路是以遗传算法为基础，在对初始种群进行遗传算子处理之前先使用模拟退火算法处理。对于求解考虑压降的换热网络，遗传/模拟退火算法的搜索计算步骤可参考文献[21]。

在遗传/模拟退火算法中增加如下求解思路，实现换热网络的同步优化改造。

第一步：对现有换热网络的结构进行分析，确定每个换热器在换热网络中的位置以及每个换热器的换热面积，即确定每个换热器进行换热匹配的两股物流的编号和所在的级数。

第二步：将现有的换热器面积Aex和现有的压降值ΔPex引入到遗传/模拟退火算法中，在遗传/模拟退火算法处理换热网络同步综合问题的同时将以上两个因素纳入了考虑，每经过一次搜索都对求得的面积和压降进行更新，如式（14）～式（21）所示，然后反馈到目标函数中。

3 实例求解

Panjeshahi等[22]对这个算例进行了研究，工艺物流数据如表1所示，相应的费用计算参数和计算公式如表2所示，物性参数如表3所示，现存的换热网络结构如图2所示。

改造后的换热网络结构如图3所示，对于每个现存换热器的新增换热面积如表4所示。总共需要新增10642.4m2的换热面积，其中E3换热器需要通 过重新配置管线来改变换热的先后顺序。改造前后压降对比如表5所示，其中流股H4不需要新增动

力设备。

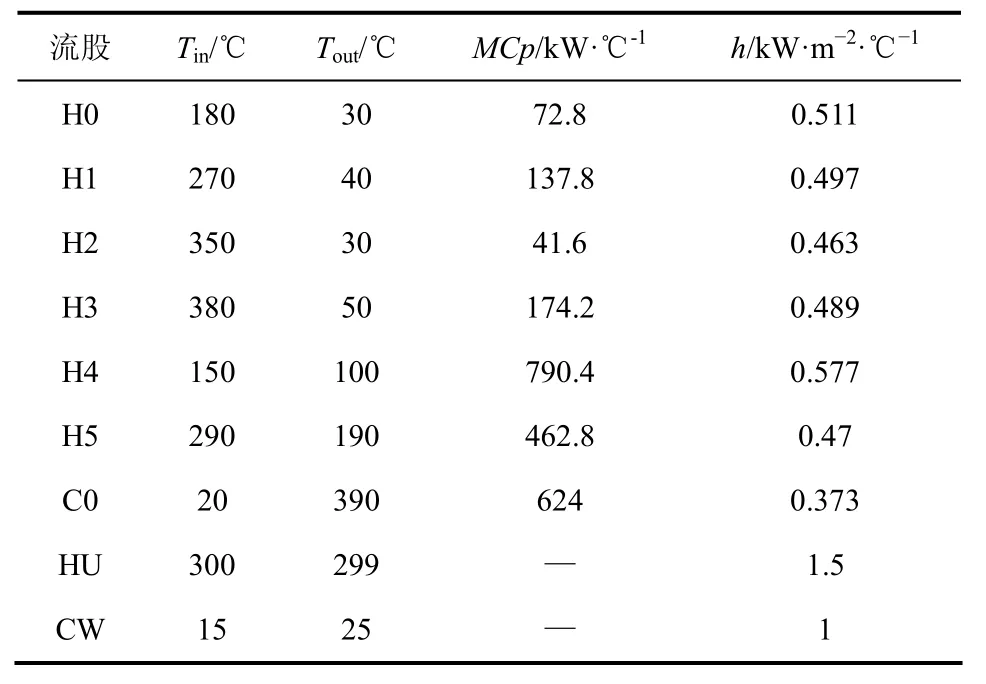
表1 流股数据

表2 费用数据

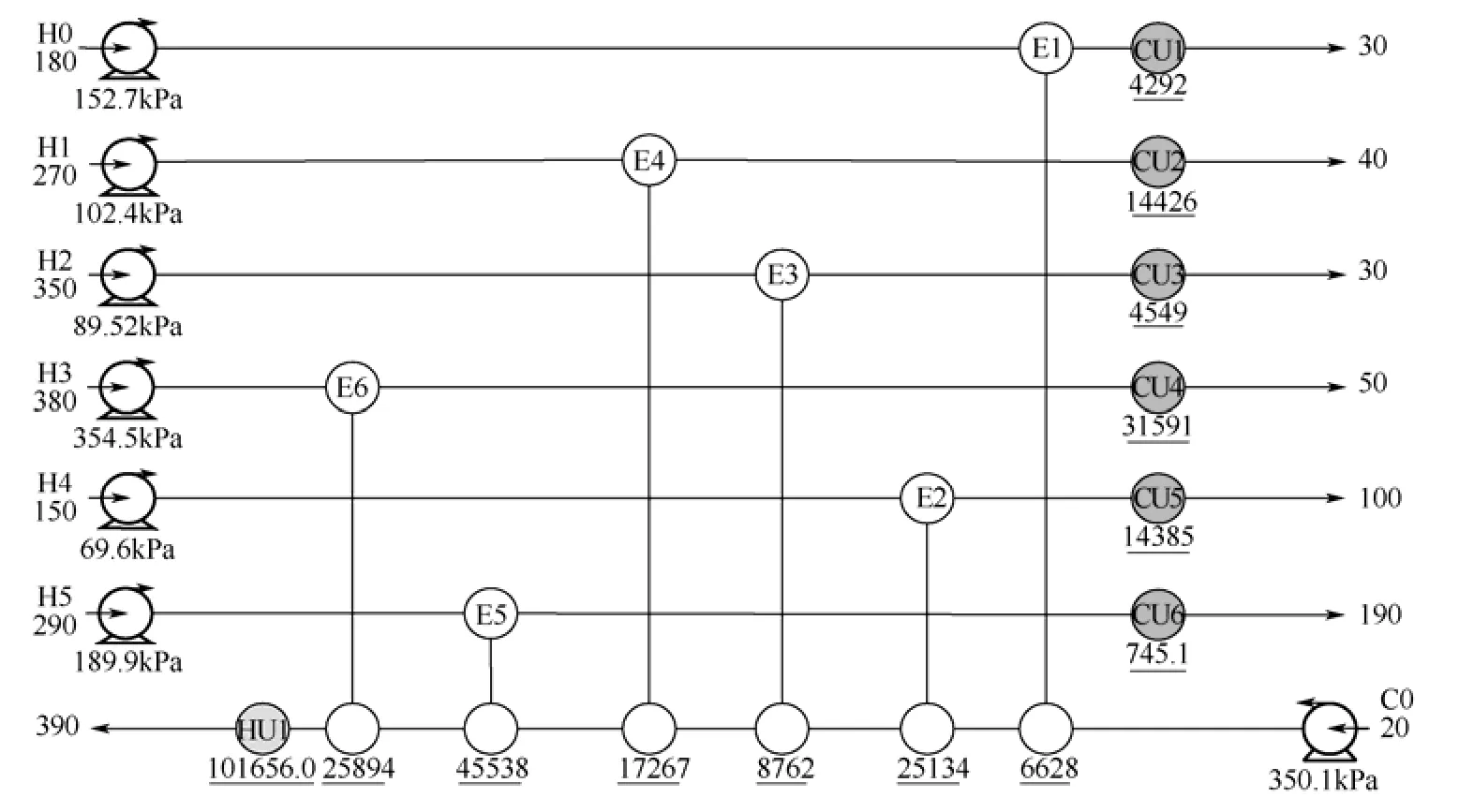
图2 初始换热网络

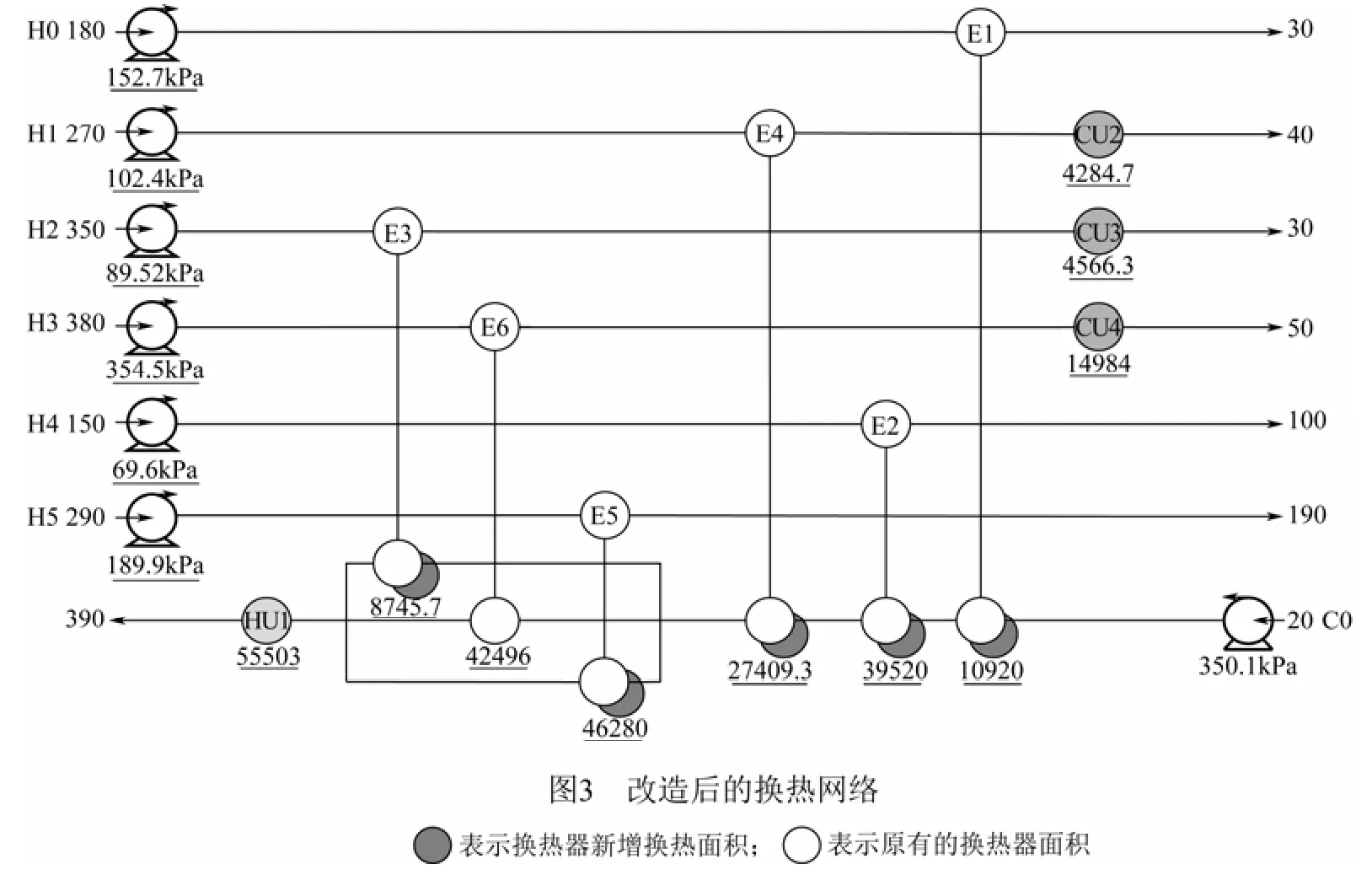
表3 物性参数

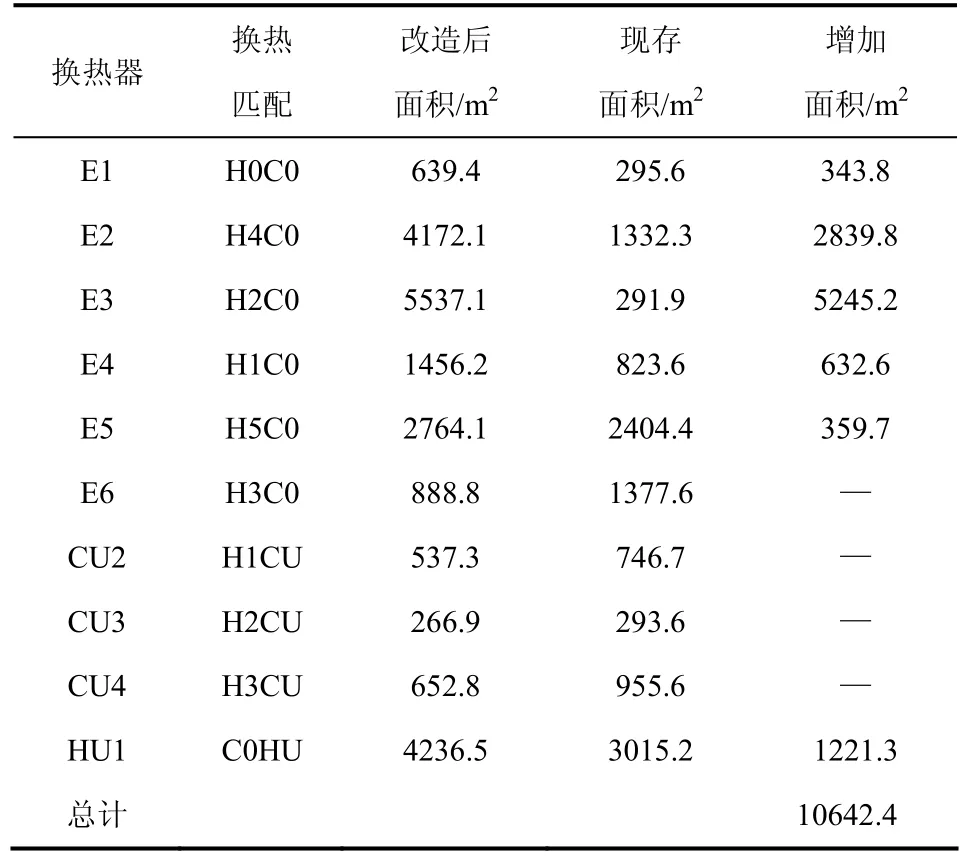
表4 新增换热面积

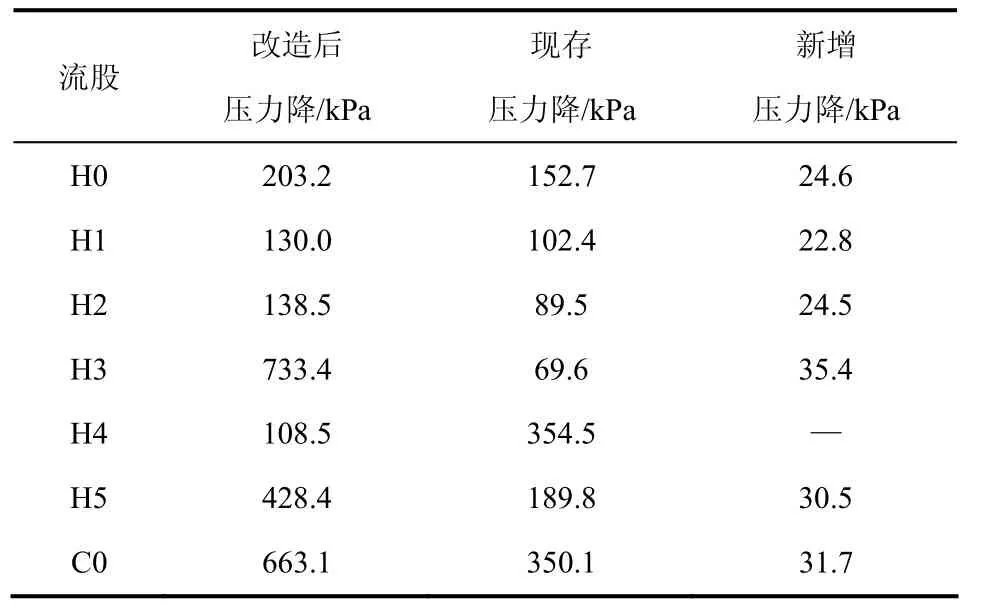
表5 新增压降

和文献计算结果的对比如表6所示。相比于文献[22]，本文所得到的改造方案需要新增换热面积为10642.4m2，面积投资和动力设备投资增加了0.79×106$；但是公用工程用量获得了较大的节省，分别减少了24.9MW的热公用工程和24.9MW的冷 公用工程，即公用工程的年度费用减少了1.92×106$/a。相比于文献[23]，本文所得到的改造方案需要新增换热面积较小，新增面积减少了21063.1m2，面积投资和动力设备投资减少了3.24×106$；但是公用工程用量节省较少，分别少节省了13.0MW的热公用工程和13.0MW的冷公用工程，即公用工程的年度费用增加了1.0×106$/a。而且，相比于文献[22-23]，本文所得到的改造方案需要增加的设备投资费的静态回收期（增加的投资费用/节省的公用工程费用）仅为0.53年。

表6 换热网络改造结果比较

4 结 论

本文对非等温混合分级超结构模型进行了改进，结合换热网络改造的相关因素，在超结构模型中综合考虑了新增换热器、现存换热器需要增加面积、现有换热器位置重新配置以及新增泵的费用等因素。所提出的考虑压降的换热网络优化改造数学模型，以最小的改造费用为目标函数，可同步优化改造换热网络，充分权衡新增面积投资、泵的投资费用以及改造后的公用工程的费用。

经过改造后的换热网络与文献[22]的结果相比，本文所得到的改造方案的面积投资和动力设备投资增加了0.79×106$，但是效果是每年的公用工程的费用多节省1.92×106$/a。与文献[23]的结果对比，本文所得到的改造方案的面积投资和动力设备投资减少了3.24×106$，但是公用工程的年度费用增加了1.0×106$/a。本文所提出改造方案增加设备费用的静态投资回收期为0.53年，小于文献数值，说明本文所提出的数学模型在优化改造换热网络的研究中，实现了用较小投资回收较多的能量，证明本文所提出的换热网络优化改造数学模型能提出更合理的改造方案。

符 号 说 明

[1] Björk K M，Nordman R. Solving large-scale retrofit heat exchanger network synthesis problems with mathematical optimization methods[J].Chemical Engineering and Processing：Process Intensification，2005，44（8）：869-876.

[2] 刘新文，罗行，马虎根. 换热网络改造可行性研究[J]. 节能，2013，32（3）：12-15.

[3] Linnhoff B，Vredeveld R. Pinch technology has come of age[J].Chemical Engineering Progress，1984，80（7）：33-40.

[4] Westerberg A W. Synthesis in engineering design[J].Computers & Chemical Engineering，1989，13（4）：365-376.

[5] Briones V，Kokossis A. New approach for the optimal retrofit of heat exchanger networks[J].Computers & Chemical Engineering，1996，20：43-48.

[6] Tjoe T N，Linnhoff B. Using pinch technology for process retrofit[J].Chemical Engineering，1986，93（8）：47-60.

[7] Ciric A R，Floudas C A. A retrofit approach for heat exchanger networks[J].Computers & Chemical Engineering，1989，13（6）：703-715.

[8] Ciric A R，Floudas C A. A mixed integer nonlinear programming model for retrofitting heat-exchanger networks[J].Industrial & Engineering Chemistry Research，1990，29（2）：239-251.

[9] Yee T F，Grossmann I E. A screening and optimization approach for the retrofit of heat-exchanger networks[J].Industrial & Engineering Chemistry Research，1991，30（1）：146-162.

[10] Zhu X X，Asante N D K. Diagnosis and optimization approach for heat exchanger network retrofit[J].AIChE Journal，1999，45（7）：1488-1503.

[11] Bagajewicz M，Valtinson G，Nguyen Thanh D Q. Retrofit of crude units preheating trains：Mathematical programming versus pinch technology[J].Industrial & Engineering Chemistry Research，2013，52（42）：14913-14926.

[12] Pan M，Smith R，Bulatov I. A novel optimization approach of improving energy recovery in retrofitting heat exchanger network with exchanger details[J].Energy，2013，57：188-200.

[13] Sreepathi B K，Rangaiah G P. Improved heat exchanger network retrofitting using exchanger reassignment strategies and multi-objective optimization[J].Energy，2014，67：584-594.

[14] Björk K M，Westerlund T. Global optimization of heat exchanger network synthesis problems with and without the isothermal mixing assumption[J].Computers & Chemical Engineering，2002，26（11）：1581-1593.

[15] 魏关锋. 用遗传/模拟退火算法进行具有多流股换热器的换热网络综合[D]. 大连：大连理工大学，2003.

[16] 霍兆义. 基于分级超结构的换热网络同步综合与改造方法研究[D]. 大连：大连理工大学，2013.

[17] 赵亮. 考虑多因素的换热网络优化改造方法研究[D]. 大连：大连理工大学，2013.

[18] Liu X，Luo X，Ma H. Studies on the retrofit of heat exchanger network based on the hybrid genetic algorithm[J].Applied Thermal Engineering，2014，62（2）：785-790.

[19] Gosselin L，Tye-Gingras M，Mathieu-Potvin F. Review of utilization of genetic algorithms in heat transfer problems[J].International Journal of Heat and Mass Transfer，2009，52（9）：2169-2188.

[20] Wei G，Yao P，Luo X，et al. Study on multi-stream heat exchanger network synthesis with parallel genetic/simulated annealing algorithm[J].Chinese Journal of Chemical Engineering，2004，12（1）：66-77.

[21] 吴敏，肖武，贺高红. 综合考虑泵的设备及运行费用的换热网络优化[J]. 化工进展，2014，33（3）：599-604.

[22] Panjeshahi M H，Tahouni N. Pressure drop optimisation in debottlenecking of heat exchanger networks[J].Energy，2008，33（6）：942-951.