基于吉布斯耗散理论的生物量收率模拟计算

戚玉，孙巍

（北京化工大学化学工程学院，膜分离过程与技术北京市重点实验室，北京 100029）

热力学在化学中占有重要地位，它可以帮助人们判断反应是否发生，以及在何种情况下发生。因而热力学分析在化学、化工和化工工艺开发过程中都处于中心地位。

在生物工艺技术中，热力学分析极少得到应 用[1]。人们都在期待，热力学分析能够预测一个给定的微生物生长过程或者新陈代谢反应是否可以发生，或者在什么条件下可以发生。基于热力学分析，可以粗略地估计微生物培养技术的关键参数，因此，可以在实验之前对微生物培养过程做经济可行性分析。当第一步实施过后，热力学分析结果将被当作参考基准，如果实验结果远不及计算结果，那么这揭示着在微生物培养过程中还有充足的空间可以提升[2]。在生物化工开发过程中，这些工作的意义不可估量。生物量收率是构成任何生物技术过程或者涉及微生物培养的实验过程的一个关键参数[3]。因为它决定了最终生物量或者细胞浓度，必须强制进行优化，以得到合理的生产率。然而，对于不同的微生物生长系统，生物量收率变化范围高达两个数量级。国外一些研究人员已经试图将一些生长过程变量（YAPT，Yave，吉布斯效率，焓效率等）用于预测生物量收率，但效果不是很理想[4]。

本文作者试图证明可以从热力学的角度来分析和预测生物量收率的变化。在基于von Stockar等的研究的基础上，本文作者在基于吉布斯耗散理论构建的生物量收率模型的基础上，尝试着将生物热力学应用到微生物生长和新陈代谢中，用碳源的一些参数，比如碳链长度及还原度等，作为估算吉布斯耗散函数的变量，探索吉布斯耗散函数和生物量收率之间的关系，以及其在实际应用中的深度及广度。

1 吉布斯耗散函数

微生物在适宜的环境条件下，不断地吸收营养物质，并按照自己的代谢方式进行代谢活动，如果同化作用大于异化作用，则细胞质的量不断增加，体积得以加大，于是表现为生长。简单地说，微生物生长就是微生物细胞组分与结构在量方面的增加，且细胞数目也有所增加[5]。同经典热力学类似，在微生物生长过程中，也存在着驱动力。而吉布斯耗散函数则同生物量收率密切相关，首先对吉布斯耗散函数进行描述。

微生物生长过程是自发的，显然这是一个高度不可逆过程，这必然伴随着熵增。与生长反应相比较，这从表面上看来似乎是矛盾的。直观地看，通过生长反应，一系列非常简单的小分子合成了高度有序的物质，这一过程的熵是减少的[6]。

将一个生长的微生物细胞视作一个开放系统并进行熵平衡分析[7-8]，如图1，物理量关系见式（1）。

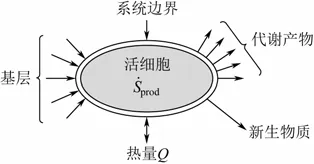
图1 微生物细胞生长过程

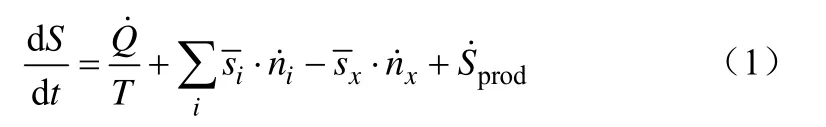
由于细胞内持续不断的熵增prodS˙ ，并且不断地有代谢物质进入细胞内，造成了熵在细胞内不断积累，这就会导致细胞死亡或者细胞组织破坏瓦解。细胞可通过向环境排出多余的熵来避免上述局面，即使得为零，细胞生长得以维系[9]。

为了表示生化反应过程中的吉布斯能变GΔ ，可以将生化反应写成宏观反应方程。以化能营养型生长过程为例，生化反应式如式（2）。

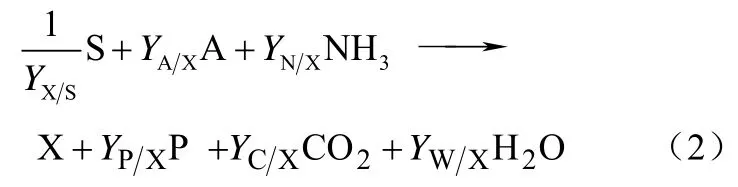
其中S、A、X和P分别表示碳源，电子受体或供体，新产生的生物量以及分解产生的废弃物。YX/S表示基于碳源的生物量收率，Yi/X表示A、NH3、P、CO2和H2O相对于X的收率。所有的Y系数都可以视作生化反应的化学计量数。对于上述反应，假设细胞处于稳定态，得到式（3）。

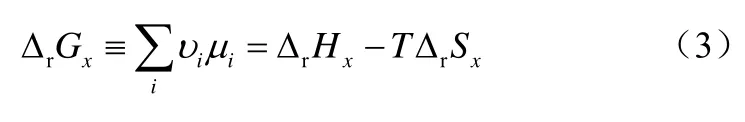
从式（3）可知，吉布斯耗散函数ΔrGx由焓和熵两部分组成，这同微生物细胞同周围环境进行的热交换及代谢物质交换的情况是一致的，所以在构建吉布斯耗散函数及生物量收率之间的关系时，可以从焓和熵的角度进行考虑和分析。

2 吉布斯耗散函数和生物量收率之间的关系

2.1 热力学模型

吉布斯耗散函数ΔrGx和生物量收率YX/S之间的关系可以通过将宏观化学反应拆分成分解代谢反应和合成代谢反应来进行描述。合成代谢反应在合成生物质的同时产生了高吉布斯能的产物，因此相当于增加了生物反应器的吉布斯能。合成代谢反应因此受到同生长过程相反的驱动力，并且是消耗能量的。合成代谢反应所消耗的能量则是由耦合的分解代谢反应来提供。分解代谢反应带来了巨大的吉布斯能耗以及释放出大量能量。折合的净吉布斯耗散函数ΔrGx显然取决于合成代谢及分解代谢的化学计量数之间的数学关系，并且可以视作微生物生长过程的驱动力。而这种数学关系可以看作合成代谢过程强加于分解代谢过程之上的一种负荷，并可以通过生物量收率YX/S来表达。

在低效率的生长体系，合成代谢反应的负荷作用很小，消耗单位碳源和能量底物仅能产生少量生物量。生物量收率可能会很小，由合成代谢反应带来的负荷几乎没有作用于分解代谢反应，这使得总的ΔrGx会是一个绝对值很大的负值。与之相对应的情况下，在高效率的生长体系中，这种负荷作用很大，并且会抵消分解代谢反应产生的ΔG，使得全过程ΔrGx是一个绝对值较小的负值。这种情况下，消耗单位底物所能产出的生物量就比较多，即生物量收率YX/S的值则会变大。极限条件下，假设这个负荷达到了一定数值，使得合成代谢反应及分解代谢反应达到平衡及ΔrGx等于零。这种情况可视作热力学第二定律下的极限最高生物量收率YX/S；而热力学平衡态下，反应速率无限慢。

在微生物生长系统中，可以预见，存在以下两种极限情况：低负荷作用，大驱动力，新陈代谢剧烈，但很少的生物量及低的YX/S；低生长速率，最高的YX/S，生长过程无限慢。所以实际的微生物生长过程中，ΔrGx和YX/S是介于以上两种极限情况之间的。

在实际生产过程中，水分、温度、酸度、含氧量等环境因素都是要精确控制的，在本文讨论的过程中，对以上环境因素都做了假设处理，假设以上因素都控制在微生物生长的最适条件下。例如，在淀粉质原料发酵酒精时，最适温度为30～32℃，最适合pH值为4.8～5，并且在好氧代谢情况下，可获得较高的细胞产量[10-11]。

为了从数学表达式上表示出吉布斯耗散函数ΔrGx和生物量收率YX/S的关系，可以把宏观反应方程划分成分解代谢和合成代谢两个部分，如式（4）、式（5）。

分解代谢部分

合成代谢部分

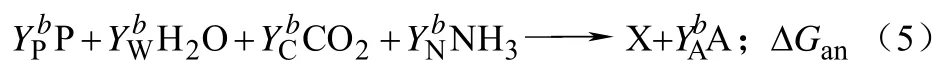
按照这种划分方式，假定碳源S首先完全被分解代谢，之后分解代谢的产物才被用于生物量的合成代谢过程。虽然这种假定是不符合实际的，但是在这种假设情况下，却可以得到简单的化学计量关系；而有了这些简单的计量关系，通过确定分解代谢反应，可以估算得到分解代谢反应的ΔG。而合成代谢反应由于其过程的高度复杂性，所以其实际反应的化学计量数不可估量。尽管对合成代谢反应进行了高度简化，只要将以上俩式合起来使用，那么计算结果就比较准确。

通过式（4）、式（5），可以得到ΔrGx和YX/S之间的定量数学关系，如式（6）。

由于生命系统是远离平衡状态的，浓度修正项就显得不是那么重要，所以可以使用标准吉布斯焓来参与计算。

2.2 微生物生长数据分析

下面从几个不同生长过程来说明吉布斯耗散函数和生物量收率之间的关系。

图2表示了吉布斯耗散函数和生物量收率之间的关系，使用的是葡萄糖基质上的耗氧生长实验数据[12]。实心符号是数据，实心符号是数 据。和YX/S数据通过生物反应量热计测得；数据由生化反应中物质的燃烧焓计算得来，下同。粗线是根据式（6）得到的吉布斯耗散函数和生物量收率YX/S的函数关系；相应的细线则是随着生物量收率YX/S的函数关系。这两条线如此接近表明，接近于零，即葡萄糖基质上的耗氧生长过程几乎就是焓驱动的，不可逆过程产生的熵基本上是以热的形式输出到外界环境中的。

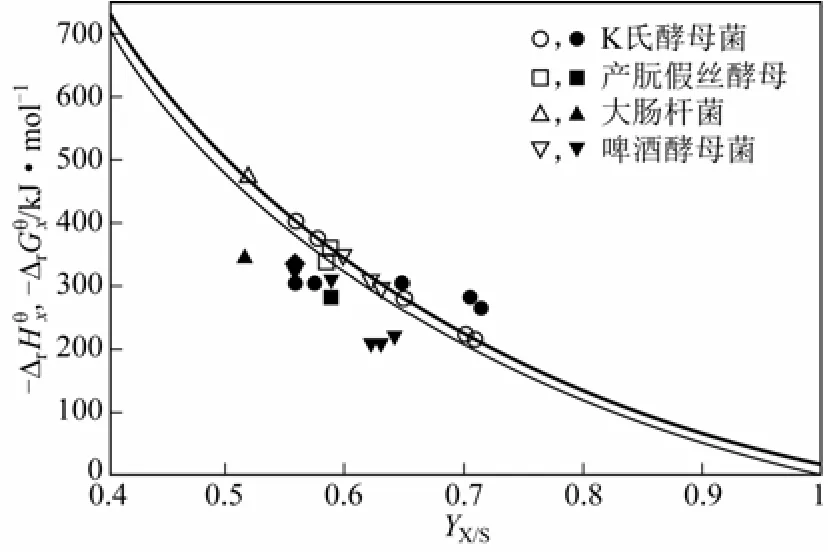
图2 葡萄糖基质上的有氧呼吸

由图2可见，对于不同菌种，不同生长条件及速率，生物量收率和反应焓变化范围很窄；虽然生物量收率较大，但和最大理论收率还是有很大差距。这同上文中提到的两种极端情况是一致的。吉布斯耗散函数大致由-250kJ/mol变化 到-500kJ/mol，测得的大致也在这个范围内 变化。

图3同图2类似，以马克斯克鲁维酵母和啤酒酵母菌的厌氧发酵为例[14]。实心符号是空心符号是数据。分解代谢反应产生了乙醇，反应方程如式（7）。

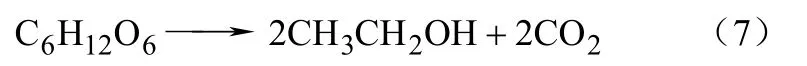
图3 葡萄糖基质上的厌氧发酵[13]

对比图2、图3可以看出，葡萄糖培养基上的吉布斯耗散函数的数量级没发生变化，但是在厌氧生长过程中，生物量收率较耗氧生长过程来说较低。由图中数据可以说明，为了维持生长所需吉布斯耗散函数，而造成了这种较低的生物量收率。

巴氏甲烷八叠球菌，是一种产甲烷菌，它可以进行代谢反应并释放甲烷[15]，反应式如式（8）。

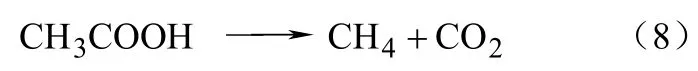
在这个过程中，产出的物质甲烷和二氧化碳的化学能比原料乙酸的化学能高得多，这就需要从环境中吸收热量来补充原料和产物之间的能量差值。同样的，的数值依然没有发生太大波动，在-500 kJ/mol左右。

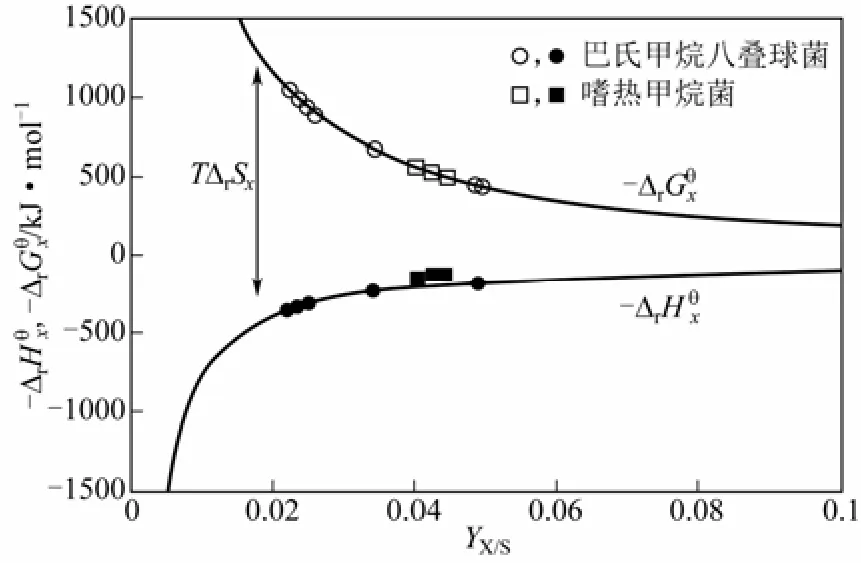
图4 甲烷菌产甲烷过程[13]

图5 焓驱动和熵驱动生长过程[13]

3 生物量收率预测

基于上文内容，将式（6）变化得到生物量收率表达式，如式（9）。

由这个式子就能计算并预测YX/S。首先可以从反应方程式（4）和式（5）来估算及，这就要求方程中的组分S、A、P已经准确定义，且化学计量数已经确定或者可以从已知条件中估算。以方程式（4）和式（5）为例，在组分A、P确定的情况下，方程中的未知数分别剩余3到4个，通过电子守恒及碳氧氮元素守恒即可求得。方程参数求得即可通过计算得到和数据，此处不再赘述。 当和 数据得出时，关键参数吉布斯耗散函数 Δ的估算至关重要。通过已经公开发表的数据分析，对于有氧呼吸生长过程来说，吉布斯耗散函数与电子受体A本身无关，和碳源的碳原子个数C及生化反应过程中的还原度γs有关。通过数据回归得到回归经验关联式如式（1）。

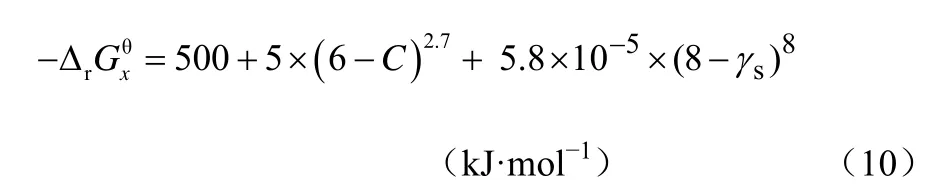
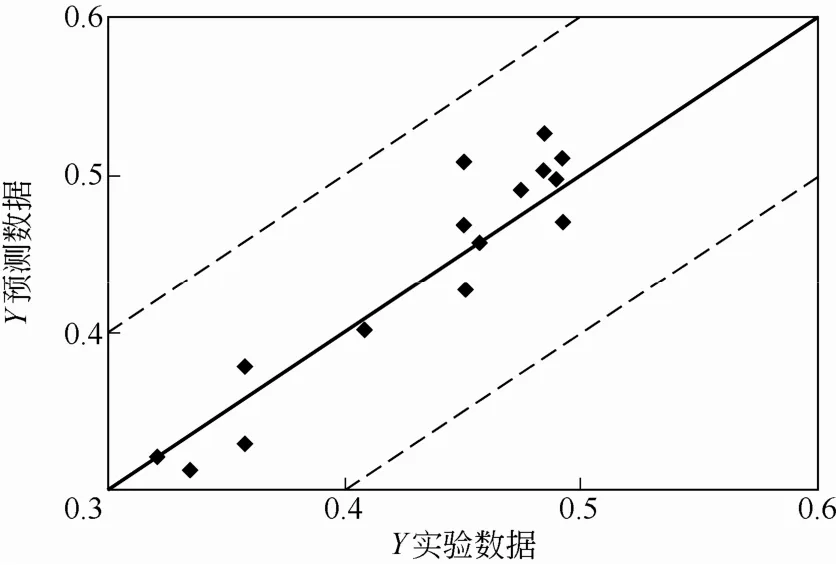
图6 预测数据和实验数据

图6中上下两条线表示±0.1偏差线，可以见到预测数据的误差大致在11%以内。这是由于在构建预测模型时只考虑了碳源的碳原子个数C及生化反应过程中的还原度γs两个参数，模型的构建还需要考虑更多参数。

4 结 论

符 号 说 明

[1] Angenent L T，Karim K，Al-Dahhan M H，et al. Production of bioenergy and biochemicals from industrial and agricultural wastewater[J].Trends in Biotechnology，2004，22（9）：477-485.

[2] Zainetdinov R I. Dynamics of informational entropy associated with self-organisation process in open system[J].Chaos，Solitons & Fractals，1999，10（9）：1425-1435.

[3] Molinuevo-Salces B，Larsen S U，Ahring B K，et al. Biogas production from catch crops：Evaluation of biomass yield and methane potential of catch crops in organic crop rotations[J].Biomass and Bioenergy，2013，59：285-292.

[4] Heijnen J J，Van Dijken J P. In search of a thermodynamic description of biomass yields for the chemotrophic growth of microorganisms[J].Biotechnology and Bioengineering，1992，39（8）：833-858.

[5] Lucia U. Thermodynamic paths and stochastic order in open systems[J].Physica A：Statistical Mechanics and its Applications，2013，392（18）：3912-3919.

[6] Marín D，Martín M，Sabater B. Entropy decrease associated to solute compartmentalization in the cell[J].Biosystems，2009，98（1）：31-36.

[7] Yu M B. Influence of environment and entropy production of a nonequilibrium open system[J].Physics Letters A，2008，372（15）：2572-2577.

[8] 蒋爱华，梅炽，时章明. 泛火用分析方法及其应用[J]. 中南大学学报：自然科学版，2011，42（2）：528.

[9] Lucia U. Irreversibility in biophysical and biochemical engineering[J].Physica A：Statistical Mechanics and its Applications，2012，391（23）：5997-6007.

[10] 岳国君. 现代酒精工艺学[M]. 北京：化学工业出版社，2011.

[11] 程坷伟，许时婴，王璋. 采用无机陶瓷膜超滤甘薯淀粉生产废液中的糖蛋白的工艺研究[J]. 食品与发酵工业，2005，30（12）：88-91.

[12] Somashekar D，Venkateshwaran G，Sambaiah K，et al. Effect of culture conditions on lipid and gamma-linolenic acid production by mucoraceous fungi[J].Process Biochemistry，2003，38（12）：1719-1724.

[13] Von Stockar U，Liu J S. Does microbial life always feed on negative entropy? Thermodynamic analysis of microbial growth[J].Biochimica et Biophysica Acta：(BBA)-Bioenergetics，1999，1412（3）：191-211.

[14] Liu J S，Marison I W，Von Stockar U. Anaerobic calorimetry of the growth of Lactobacillus helveticus using a highly sensitive Bio-RCl[J].Journal of Thermal Analysis and Calorimetry，1999，56（3）：1191-1195.

[15] 佘晨兴，仝川. 自然湿地土壤产甲烷菌和甲烷氧化菌多样性的分子检测[J]. 生态学报，2011，31（14）：4126-4135.

[16] Annila A，Salthe S. Physical foundations of evolutionary theory[J].Journal of Non-Equilibrium Thermodynamics，2010，35（3）：301-321.