空化射流流场数值模拟的研究进展

林兴华，张敏革，秦青，党明岩

（1沈阳理工大学环境与化学工程学院，辽宁 沈阳 110159；2天津科技大学机械工程学院，天津 300222）

空化是指在液流系统中局部压力小于饱和蒸汽压时产生空化气泡的现象，而空化射流是卷入了这种空化气泡的一种连续射流。空化气泡在射流流动过程中会进一步生长，直到遇到阻滞时引起破裂，并在溃灭时能够产生瞬间的高温高压，对构件表面具有巨大的腐蚀作用。虽然单独的空泡溃灭产生的破坏强度较小，但持续的射流冲击会使此现象得以扩大，在航海和水利设施等领域造成了严重的影响。但如果将其应用到工业切割、石油钻井、化工清洗、废水处理等行业中[1-2]，空化射流又以其效率高、耗能少、无污染等巨大优势取得了不可忽视的贡献。因此，对空化射流的进一步研究深受广大研究人员的青睐。现在的实验研究主要集中在驱动压力、温度、喷头结构和构件材料等因素对空化射流的影 响[3-5]，但是由于实验研究无法清楚地观察到流场的内部情况，使得空化射流的流场结构及空化气泡的动力学性能仍存在盲区[6]。

计算流体力学（CFD）是一种以计算机计算为基础，对流体的传质传热等现象进行分析的研究方法。随着近代计算机技术的发展，通过数值模拟来研究空化射流成为一种新的分析手段，对于研究流场结构等微观问题而言，CFD也是唯一可靠的求解方法。但由于空化射流中伴随着介质密度的剧烈变化和复杂的湍流两相区，使得在空化射流的数值模拟过程中，对空化模型、湍流模型、两相流模型以及数值计算方法的选择仍需要继续探索，以便建立更加高效准确的数值模拟方法来再现空化射流的物理本质。

本文通过对模拟过程中的数值模型、数值计算方法和流场特性研究进行综合论述，阐述了不同模型和计算方法的优缺点及其研究进展，对其存在的问题进行了分析，并对以后的研究方向进行了展望。

1 空化射流数值模型

1.1 空化模型

空化射流的计算模型是在流体遵守质量守恒、动量守恒和能量守恒等物理守恒定律的基础上，通过求解N-S方程及Rayleigh-Plesset方程进行的。这种研究始于19世纪下半叶，但由于存在过多的假设使得结果与实际情况存在较大偏差，因此现代的研究便在此基础上尽量减少前提假设，发展更加符合实际的空化模型。这些研究可根据气液两相之间是否存在明显界面而分为两类：界面跟踪法和均质平衡流模型。

1.1.1 界面跟踪法

与普通射流相比，空化射流所含的空化气泡在刚性壁面附近或在压力梯度的作用下会发生破裂，而空泡溃灭时会产生微射流和巨大的冲击波，因此研究空泡的破裂方式及特性，能够更加具体地了解空化射流的作用机理。界面跟踪法的特点是假设两相之间存在明显的界面，可以清晰地再现空化气泡在溃灭时的形态特性，同时假设空泡内的压强保持为汽化压强，并且气体是连续的，因此不用考虑空泡内的流动情况，只考虑液相中的控制方程即可。它的基本原理是将守恒定律应用到气液两相的界面，通过迭代计算确定新界面的位置和新界面上的物化特性。

根据这一原理，发展出了许多数值计算方法，其中边界元法是该类计算方法的代表，在实际应用中也是最为广泛。Reichardt等[7]最早利用分布面源的方法，解决了由于空泡尾流压力回复导致的数值不稳定的问题；此后许多研究人员[8-9]利用边界元法对空化射流中黏性和非黏性流体产生的空化现象提出了非线性的分析方法，并对三维模型中的非定常空化射流的预测方法进行了改进，很大程度上解决了由于界面跟踪法只考虑液相，很少能给出控制附着空泡的机制，使得一般的边界元法在解决非定常流动的问题时存在的困难。此外，Bal等[10-11]还通过边界元迭代法对空化气泡溃灭时的表面性质进行了研究，并对水翼在有限深度水域中的空化现象以及水的波动对其影响作了深入的分析，对边界元法在空化射流的数值模拟的应用上起到了推动作用；Akira Sou等[12]利用欧拉-拉格朗日气泡跟踪法深入研究了柴油机喷液射流中的空化现象，对空泡溃灭时的形态特性进行了很好的再现，对空化区域的长度和厚度进行了定量预测。

但是对于空化射流的数值模拟而言，由于同时存在可压缩区域和不可压缩区域，使得数值模拟中最大的困难在于完整地描述空化射流中流体密度的剧烈变化，而界面跟踪法无法很好地适应这种剧烈的相变化，也因此限制了这类模型的应用，目前常被用于一些可以将空化气泡视为纯气体全封闭气泡的简单问题中。

1.1.2 均质平衡流模型

均质平衡流模型是假设气液两相之间没有明显的界面，将流体视为一种同时存在两相的混合物，通过流体的密度场和体积分数的变化来描述空间中两相的分布。在空化射流当中，空化气泡是随机分布在射流当中，随流体介质一起流动并生长，并且空泡内的压强也会在流动过程随温度、流速等因素一起变化，因此对于研究空化射流的整体特性而言，均质平衡流模型的原理更加趋近空化射流的实质，在这类方法中单流体模型和双流体模型是两个主体代表。

双流体模型是假设气液两相在流场中呈现均匀分布，并且每一相都由各自的状态方程进行控制，因此气体和液体的运动状态是分别进行计算的。通常将质量、动量和能量作为变量，通过求解Rayleigh-Plesset方程，如式（1），对气泡的体积变化进行计算，这种模型可以清楚地表达空化射流的物理特性，因此许多学者利用这种方法对空化射流的机理及特性做了大量研究。例如，Battistoni等[13]以柴油机的喷射射流为研究对象，利用双流体模型对流体介质分别为柴油和大豆油时产生的空化现象作了对比分析；Vijayakumar等[14]在此基础上基于双流体模型，对流体介质分别为二乙酯、二乙醚和生物柴油时产生的空化现象作了研究分析，得到了流体性能对喷射空化射流产生的影响；王国玉等[15]基于液相和气相的状态方程，推导出了混合介质的密度在一般曲线坐标系下的控制方程及有关的计算公式，并在管道水锤的空化流动试验中进行了验证。这些研究表明，在片状空化的模拟中双流体模型的模拟准确度很高，但是由于双流体模型中没有统一的数值模型来联系气液两相，从而忽略了两相间的输运和对流现象，使其在空泡闭合区中无法很好地捕捉空泡流动的特性，因此这种空化模型目前仅被用在空化现象不明显的射流模拟中。

Rayleigh-Plesset方程：

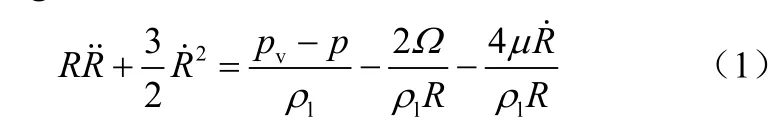
式中，R为空泡半径；R˙为空泡增长速度；R˙˙为空泡增长加速度；Pv为水的饱和蒸汽压；P为液体压力；Ω为表面张力；ρl为液体密度。

单流体模型是建立在混合物各相体积分数或质量分数上的传输方程，与双流体模型不同，这种空化模型忽略了两相之间的速度滑移，将射流中的流体作为一种均匀的混合物，其物理性质由气相的体积分率所决定，所以这种“假单相”流体的密度不再是某个定值，而是介于气相和液相密度之间的某个区间，并且对射流中蒸发和冷凝现象发生的条件进行了合理假设，由此使得两相之间的输运和对流现象得以体现[16]。利用这种原理，开发出了多种适合空化射流的单流体模型，如Merkle模型、Kunz模型、Zawart模型等。其中Singhal等[17]在Kubota模型基础上考虑了非凝结气体和气泡的相对运动、表面张力等因素对空化射流的影响，建立了蒸汽质量分数输运方程，用于复杂的空化流的计算；Saito等[18]在Merkle模型的基础上，将输运方程的相变源项中加入了饱和蒸汽温度的条件，对该模型进行了修正；Owis 和Nayfeh[19]考虑液体的压缩性，引入 Peng-Robinson 状态方程来分别计算液体和蒸汽单相的密度，对Kunz模型进行了优化。但是在这些模型中，大多是将气相的体积分数作为变量，通过求解Rayleigh-Plesset方程来确定“假单相”的物理性质，对于气泡的表面张力则是通过子网格模型进行处理，这些处理手段和模拟技术都需要大量的经验系数来封闭控制方程，因此为了简化计算，假设空泡之间不存在相互作用力[20-22]，所以这种模型依旧无法完全再现空化射流中热力学或动力学的非平衡特性。但是与其他模型相比，这种模型更加接近空化射流的真实情况，并且对气泡簇运动的处理简洁方便，准确性和适应性都处于一个合理的水平，使之成为目前应用最为广泛的空化模型。

1.2 湍流模型

在空化射流的研究中，选取合适的湍流模型对于准确预测空化射流特性具有重大意义。现有的湍流模型大致可以分为三类：直接数值模拟（DNS）、大涡模拟（LES）和雷诺平均数值模拟（RANS）。

RANS模型是在求解过程中只注重流场参数的平均信息，使得计算精度和计算成本都处于较合理的水平，是现在应用最为广泛的一种模型。在这种模型中，以19世纪后期Boussinesq提出的k-ε两方程湍流模型最为代表性，许多学者在对柴油机各种类型的喷嘴等物理模型产生的空化射流进行数值模拟研究时，利用这种模型对其湍流动能和湍流黏度进行描述[23-24]，所得模拟结果都能很好地与实验结果相吻合，证明了这种湍流模型在空化射流模拟中的适用性。但研究结果同时表明，不同形式的k-ε模型在不同的物理模型产生的空化射流中的模拟效果也略有差异。钱忠东等[25]对比分析了3种k-ε模型在空化射流中的模拟效果，发现Standardk-ε模型对空化数不敏感，但精度不高；RNGk-ε模型计算精度较高，对空化数不敏感；Realizablek-ε模型对空化数敏感，精度与RNGk-ε相差不大。卢义玉 等[26]应用标准k-ε模型、RNGk-ε模型和Realizablek-ε模型对缩放型喷嘴产生的空化射流流场分别进行了数值模拟分析，发现RNGk-ε模型的模拟结果最接近实验中所得的湍流流场。刘思孝[27]在模拟低压自激脉冲空化射流内部流场时，发现由于流场内存在高强度的涡环和低雷诺数区，使得标准k-ω模型和SSTk-ω模型更加适合。

DNS方法是通过直接求解N-S方程来预测流场内所有参数的全部信息，因此无需引入任何湍流模型，对湍流本质的描述更加精准。但这种方法需要非常紧密的网格（网格数达109～1012）和非常小的时间步长（10～100μs以下），使得这种方法只能对非常简单的湍流进行模拟[28]。LES方法是一种介于DNS和RANS之间的模拟方法，它是利用滤波函数对N-S方程进行预处理，仅对大尺度脉动进行直接模拟，对小尺度的则进行假设，在湍流发展过程中能够对一些细节进行更加细致的模拟，使得计算精度高于RANS方法，在近十年的时间内得到巨大发展，现已广泛应用到各种空化射流的数值模拟中[29-31]，但是其计算量虽然比DNS小了很多，却依然对计算机的内存等条件要求很高，使其目前在工程上的应用范围远远不如RANS方法[32]。相信随着计算机硬件技术的发展与普及，这种方法在应用范围上也会更广。

1.3 多相流模型

在空化射流的流场中因同时存在气液两相，所以在进行数值分析时要根据所研究对象选取合适的多相流模型。现在广泛使用的模型有：VOF模型、混合模型和欧拉模型。

VOF模型是通过求解单独的动量方程和体积分数方程来模拟两相界面上的瞬间动态。Chen等[33]利用VOF模型对空化射流冲击到钢铁表面时的瞬间进行模拟，证实了空化气泡对钢铁腐蚀的主要原因在于气泡溃灭时产生的冲击波；张晓东[34]运用VOF模型对竖井旋流式泄洪洞产生的空化现象进行了三维数值模拟，得到了螺旋空化射流的流态、流速、压强、消能率等各项水力参数，很好地再现了试验结果。这种方法将空化射流中的气相和液相分离开，对于研究空化射流的整体特性时不太适合。

混合模型考虑了界面传递特性及两相间的扩散和脉动作用，主要用于模拟不同速度的多相流和具有强烈耦合的各向同性多相流。欧拉模型则是将每一相都看作为充满整个流场的连续介质，主要用于可作连续介质进行研究的多相混合物的数值模拟中。这两种模型也是目前研究空化射流时最常用的多相流模型，因为混合模型比欧拉模型少解一部分方程，因此计算时间更快，在计算稳定性方面，复杂的欧拉模型也会稍逊一筹，但是欧拉模型的计算精度要高于混合模型。总体而言，混合模型主要用于研究空化发生的位置和强度等问题，而欧拉模型则主要用于需要对流场内两相分布情况进行细节描述之时。Li等[35]利用混合模型对挡板喷嘴中的空化射流产生的位置进行了实验和模拟研究，发现低雷诺数射流中空化气泡产生的位置主要位于喷嘴出口的尖角处和挡板的边缘处，在高雷诺数射流中，片状空化气泡主要随分散流发生在挡板的弯曲表面上，云状气泡主要随喷射流出现。Postrioti Lucio等[36]在对柴油机注射系统中的空化现象进行实验和数值研究时，采用欧拉混合模型对喷口处的流速和湍流强度等参数进行模拟计算，得出的结果与实验完全吻合。

2 数值计算方法

空化射流是一种非常复杂的流动体系，这个体系包含了流体形态的剧烈变化、空化气泡的爆炸及冲击波的影响等多种现象，因此对空化射流的模拟计算方法也提出了更高的要求。目前常用的两种计算方法为拉格朗日计算方法和欧拉计算方法，这两种方法对于模拟空化射流而言各具优势，又存在各自的不足。其中，拉格朗日计算方法可以使网格结构随着流体形态或构件材料形状的变化而产生适应性的变形，从而实现了空化射流在模拟中对流体形态变换特性的计算，但是这种方法的计算网格在剧烈的空化区域等极端复杂的情况下会发生严重的扭曲或纠结现象，对计算结果的准确性造成负面影响；欧拉计算方法中的计算网格在空间中是固定的，消除了在剧烈空化等区域的失真问题，但是由于相对较短的计算时间步长，导致气液两相交界面上的对流问题容易出现计算错误。

为此，许多学者为寻找一种适合于模拟空化射流的计算方法做了大量努力[37-39]，Xie等[40]提出了一种简化的虚拟流体模型来模拟空化射流中气泡的爆炸现象，用另一个等熵单流体空化模型来描述和捕捉非定常的空化射流形态，在模拟淹没空化射流冲击自由壁面中得到较好的结果。Wang等[41]综合了拉格朗日计算方法和欧拉计算方法的优点，提出了一种混合计算方法，对剧烈变化的空化区域通过欧拉模型进行计算，对于相对固定的刚性壁面等位置通过拉格朗日网格进行计算，提高了空化射流的模拟精度。

但是由于空化射流同时存在不可压缩的液相区域和可压缩的气相区域，并且这两个区域存在随时进行转换的可能，即存在不确定的过渡区域，使得计算方法需要满足这两种截然相反情况的同时，还要适应过渡区域中剧烈的相变化，因此这种计算方法比普通的计算方法要有更大的适应能力，同时上述的解决案例中也仅是在解决个别问题中适用，对于空化射流模拟的通用计算方法目前还没找到。通常所应用的不可压缩流体的方法都需要通过相应的方程对压力进行修正，例如SIMPLE和PISO等计算方法，但这些方法在应用时，由于需要考虑在空化区域内速度的变化和气相的可压缩性，使得在气液交界面上出现计算错误。另一方面，常用的可压缩求解方法是通过状态方程对压力进行计算，但这种方法在低流速的情况下会导致计算结果很难收敛，这时需要对流体进行预处理[42]，使流速更接近于对流速度，以此来解决计算结果难收敛的问题，但这种预处理又会使误差相对增大。

可见，目前对于空化射流的数值模拟还没有形成一种完全合适的计算方法，具体来讲就是缺少一种能够同时计算液相和气相的通用计算方法。相信随着以后研究的深入，通过对有限体积法、有限元法等方法进行不断改进和融合，使相应的数值计算方法趋于完善，将会对空化射流流场分析起到推动作用。

3 空化射流流场特性的数值分析

在CFD技术应用到空化射流的研究之前，对空化射流流场特性的认识主要依靠实验手段来进行，但由于实验手段的局限性，使得人们对于空化射流复杂的内部流场结构及其影响因素的认识存在盲区，这也限制了对空化射流的有效应用。随着商用CFD软件的开发与普及，以及对空化射流数值模型的逐步优化，最终实现了空化射流内部流场结构的可视化，大大增进了人们对空化机理及空化流场特性的认识[43-45]。

Echouchene等[46]基于Fluent商用软件，利用Singhal空化模型对柴油机喷嘴中的空化射流流场特性进行了模拟研究，尤其针对喷嘴壁面的粗糙度对空化流场的影响进行了细致分析，如图1，其中Ks为壁面凸起的高度，Z为喷嘴结构的轴向距离，原点位于缩口处，D2为缩口处的直径。从图1中可以看出，在Z＜0的区域，射流中只有液相一种流体，但是当射流到达缩口处时，流体形态会发生急剧的变化，使得射流当中同时存在气相和液相两种流体，即产生空化现象；在注射压力较低时，壁面的粗糙度对空化区域的长度具有明显的影响，粗糙度越高，空化区域越短；在注射压力较高时，壁面的粗糙度对空化现象的影响很小。

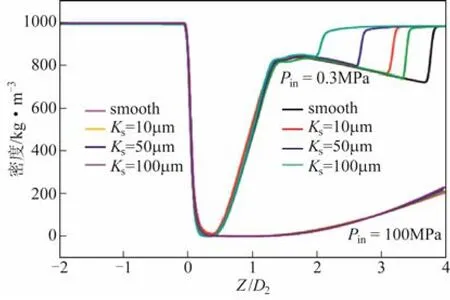
图1 壁面处射流密度随粗糙度的变化曲线[46]

邓松圣等[47]选用k-ε湍流模型和SMPLEC算 法，通过数值模拟的方法研究了角形喷嘴结构对空化流场的影响。研究结果表明，喷嘴结构中的扩散角对空化流场结构的影响较大，如图2所示，随着θ的增大，负压越来越不明显，在30°时空化效果最好。扩散段和圆柱段的长度对喷嘴内流场结构的影响较小，但也存在一定的最佳范围，其中扩散段长度如果过小会影响空化气泡的数量，过大则会使喷嘴的出口速度过小，影响空化气泡的发展，而圆柱段长度在4mm左右时最有利于气泡的发展。

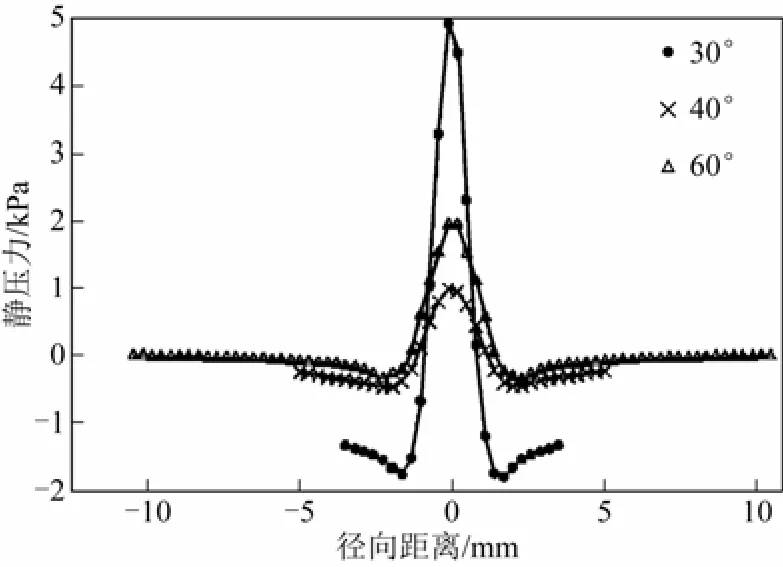
图2 不同θ值扩散段中截面压力分布曲线[47]

He等[48]以柴油机阀封闭喷头为物理模型，对喷嘴中的空化射流特性做了数值模拟研究，对比分析了注射压力分别为12MPa和100MPa时，喷孔入口处的曲率半径对空化射流流场特性的影响，其变化曲线分别如图3(a)、(b)所示，其中r表示入口处的曲率半径，Cd为流量系数，K为空化数，其表达式分别如式（2）、式（3）。

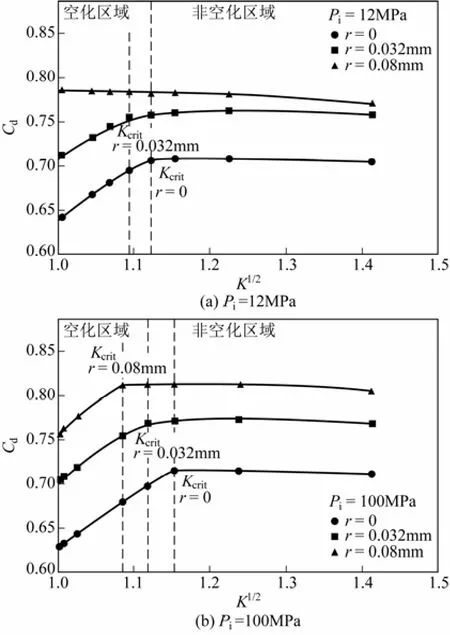
图3 不同曲率半径下流量系数随空化数的变化曲线[48]

式中，m˙为实际质量流率A为喷孔的横截面 积；ρl为液相密度；pi为注射压力；po为喷孔的出口压力；pv为气体饱和蒸汽压。

由图3可以看出，当注射压力较大时，空化现象对射流的流率具有明显的影响，并且存在一个临界空化数Kcrit。当K＜Kcrit时，流量系数Cd与空化数K之间存在一种正线性关系；当K＞Kcrit时，射流中就只有液相一种形式，此时空化数K主要由雷诺数所决定的，基本保持不变；随着喷口入口处曲率半径的增大，流量系数Cd明显增大，而临界空化数K则相对减小，所以空化现象越不容易发生；当注射压力较小时，随着曲率半径r的增大，临界空化数Kcrit逐渐消失，这就说明如果曲率半径无限大，或是注射压力足够低，喷头内的射流将不会再产生空化现象。

Salvador等[49]通过双流体空化模型，对流体性质与空化射流流场特性之间的关系做了数值模拟研究，对比分析了普通柴油和生物柴油对空化射流产生和发展的影响，其中两种燃料的物理性质如表1。在注射压力为80MPa、围压分别为17MPa和18MPa时，空化射流中的气体含率分布云图如图4所示。由此可以看出，普通柴油所产生的空化区域要大于生物柴油，说明流体的密度和黏度越大，对射流中的空化现象越能够起到抑制作用。

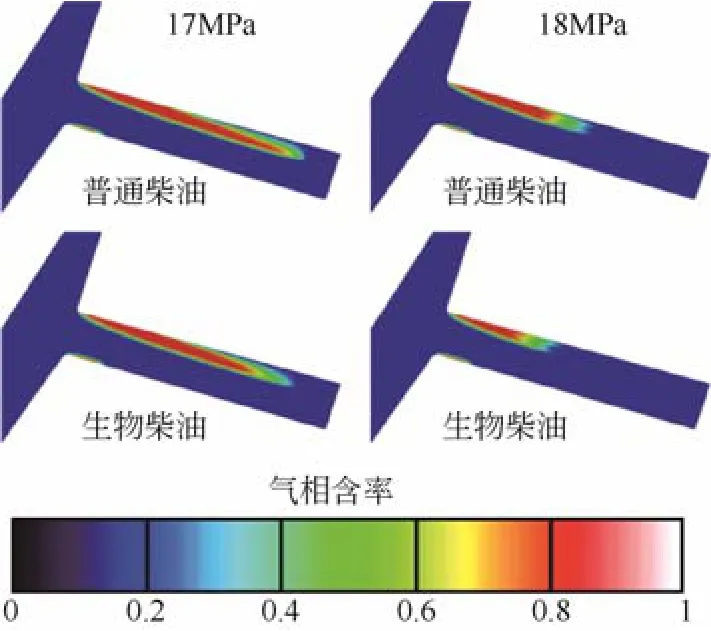
图4 两种燃料空化射流中气体含率分布云图[49]

表1 两种燃料的物理性质

Wang等[50]对注射压力波动与空化射流流场特性之间的关系做了数值模拟研究，模拟过程中入口压力设置为正弦波动压力，其控制方程如式（4）。

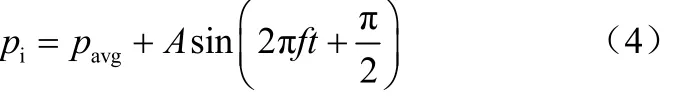
式中，pi为瞬时注射压力；pavg为平均压力，110MPa；A为振幅；f为频率；t为模拟时间。

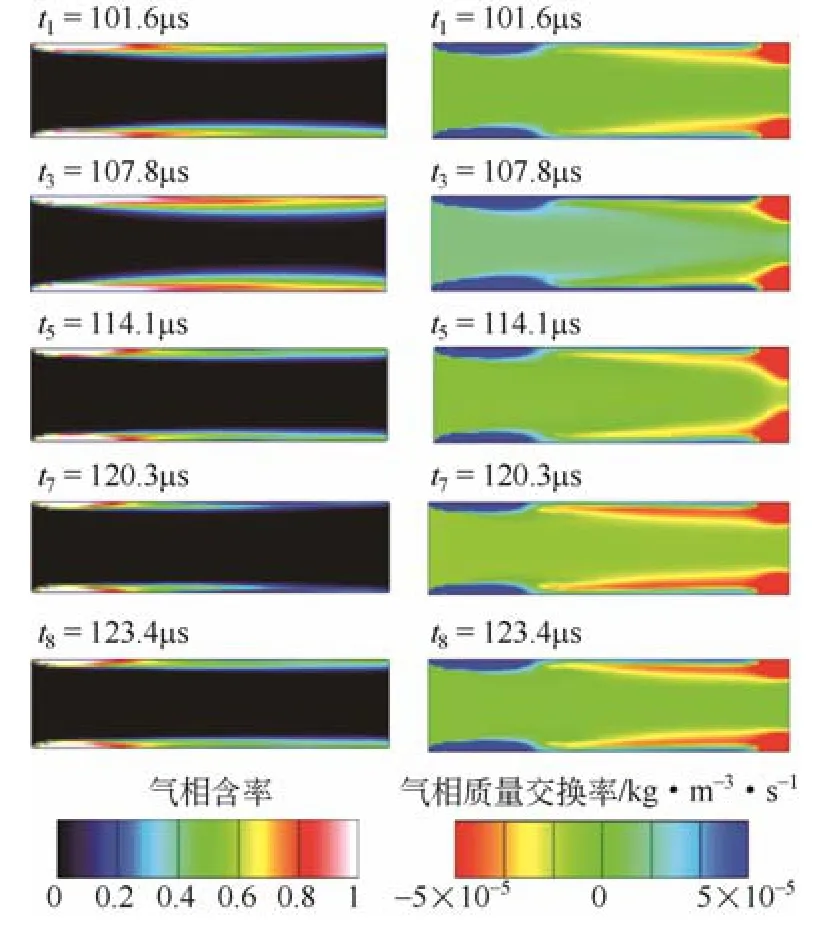
图5 空化射流流场随入口压力波动变化云图[50]

选用频率f为40kHz、振幅A为11MPa的波动压力，通过空化射流流场内的气相含率和气相质量交换率来描述流场特性随时间的变化，如图5所 示，其中气相质量交换率为负值时，代表空化气泡的溃灭，为正值时代表空化气泡得以发展。由图5可以看出入口压力的波动情况对喷孔入口处的空化现象没有明显影响，但是对于空泡尾流区域的影响很明显。这是由于在入口处存在大尺度的涡流，使得该处具有足够大的液相张力来维持空泡的生长，因此入口压力的波动对该处的空化现象影响不大，但是在尾流区域由于射流中的漩涡变弱，使其与空化气泡之间的作用力相对扩大，从而使空化现象对入口压力的波动情况更加敏感；同时可以看出随着注射压力的波动，空化射流流场内的空化区域也呈现周期性的变化，并且通过进一步分析得知，空化区域的变化规律与注射压力的时间导数dpi/dt之间呈现密切的负相关关系，因此可以将dpi/dt作为预测空化射流流场变化特性的一个重要参数。

Mohammad等[51]则通过数值模拟的方法研究了柴油机内因空化现象对柴油喷雾的影响，数值分析中以入口侧的曲率半径R与收缩段直径D的比值作为描述空化现象的变量，并以此分析空化对喷雾特性的影响。研究结果表明，当R/D=1时，开始出现空化现象，并对喷雾的喷射深度具有很大的影响；当R/D=0时喷射深度达到最大，随着R/D的增大，喷射深度逐渐减小，并且造成空化气泡溃灭速度减小；同时发现在喷雾开始阶段，数值计算结果与实验结果相差较大，如图6。这是由于在喷雾开始阶段，空化气泡没有充分的溃灭，并且产生的液滴处于不稳定的状态，因此在初始阶段液滴的尺寸是一个变量，随着喷雾的继续进行，空化气泡溃灭频率减小，液滴的尺寸和索特尔平均直径也趋于一个定值，这与实验结果是相吻合的。

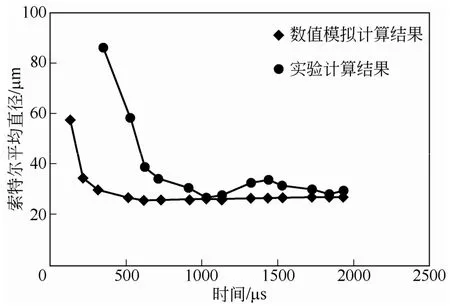
图6 索特尔平均直径随时间变化曲线（R/D=0）[51]

综上所述可知，目前运用数值模拟的方法来研究空化流场已经日渐成熟，也取得了相当大的成果，使复杂的空化流场开始变得生动形象。但是对 空化流场研究的最终目的是为了更好地利用这种能量，而目前对空化气泡在构件表面破灭时产生的冲击波的分布特性，以及空化现象对射流冲击力的具体影响还主要依靠实验研究[52-54]。数值模拟在此方面的研究依然很少，目前的研究成果大多只是宏观上的定性描述，很少给出定量的表达，因此在以后的研究中，尝试通过数值模拟的方法来定量分析空化射流在构件表面的冲击力的大小及分布特性，会为以后更好地应用空化射流提供更为有利的依据。

4 问题与展望

空化气泡的存在使空化射流成为一种复杂的非定常现象，而对于空化射流作用力的应用主要是希望空化气泡能够在特定的区域溃灭，从而使其产生的冲击力得以控制，所以研究空化气泡在生成、发展和溃灭过程中的相互作用是有效应用空化射流的前提，而研究空化射流在构件表面的冲击腐蚀性能的大小、分布及影响因素则是主要目标。

目前研究空化射流中气泡之间的相互作用，常用的有两种方法：一种是宏观地观察气泡簇的运动状态，通过研究两相流界面处的作用力来估算气泡簇内部中的相互作用；另一种方法是通过跟踪观察某个气泡表面的运动，来研究单一气泡的微观运动状态[55]。但是这两种研究方法存在以下几点问题：第一，空化气泡内部的压力不仅仅依赖于周围液体的压力，还与气泡的运动状态有关，但是在计算过程中为了减小计算的难度和时间，通常将气泡内的压力近似于外部液体的压力，因此在空化区域内压力冲击波的传递存在计算误差，空化气泡溃灭时产生的冲击力也因此与实际情况不符；第二，由于气泡产生的震动频率很大，使得这种复杂的流动体系在模拟过程中存在时间过长的问题；第三，空化气泡运动状态的模拟计算通常是由Rayleigh-Plesset方程进行控制的，但这需要对空化气泡周围液体压力和气泡内部压力进行预先的设定，而这需要大量的经验系数来封闭控制方程，由此对射流中空泡的运动状态的模拟容易造成失真；第四，空化射流数值模拟研究方法中的界面跟踪法对于了解空化气泡的物理结构及产生的作用力拥有很好的帮助，同时均质平衡流模拟方法可以很方便地估算冷凝和气化等过程中存在的传质与传热。但是这些研究都是集中于微观方面的研究，对于解决估算工程上存在的实际问题仍存在很大的难度。此外，由于在模拟过程中没有一个特别适合的物理量来真实描述空化射流到达构件表面后冲击力及冲击波产生的影响，使得对于空化射流冲击腐蚀性能大小和分布特性的模拟研究目前还很少，虽然有人曾尝试通过构件表面处压力的波动或流体的动压来表征冲击性能的影响[56-57]，但是这些方法仅是对射流中部分作用力作出了描述，对空化射流本身所具有的综合冲击腐蚀性能依然无法清楚的表达。

因此，对于以后的空化射流数值模拟研究而言，重点应在于以下几点：首先，可以尝试将界面跟踪方法与连续性模型所拥有的各自优点结合起来，找出一种新的空化模型来更加准确地再现空化射流的物理过程；其次，综合空化射流的特点，发展联系间接算法与直接算法的通用算法，也是以后研究空化射流数值模拟的一项重大任务；最后，结合空化射流冲击性能的实验研究结果，分析得出影响其冲击力大小和分布特性的各项因素及表达式，从而找出一套适合数值模拟研究的表征方法，实现对空化射流冲击性能进行定量预测的目的。

5 结 语

通过对空化射流流场数值模拟中的数值模型、数值计算方法和空化流场特性的研究进展进行综合论述，提出了目前研究中所存在的问题，从而为以后的研究探索提供了思路。由于空化射流复杂的两相湍流混合区和强烈的密度变化等因素，使得对其进行数值模拟提出了巨大挑战，通过根据所研究的内容，选取合理的模拟模型和模拟方法，将有助于最大程度上还原空化射流的物理特性，随着计算机技术的发展和模拟方法的改进，以后对空化流场的模拟研究将取得更大的进步。

[1] Soyama H，Takakuwa O. Enhancing the aggressive strength of a cavitating jet and its practical application[J].Journal of Fluid Science and Technology，2011，6（4）：510-521.

[2] Axinte D A，Karpuschewski B，Kong M C，et al. High energy fluid jet machining （HEFJet-Mach）：From scientific and technological advances to niche industrial applications[J].CIRP Annals- Manufacturing Technology，2014，63：751-771.

[3] Liu Xiumei，Long Zheng，He Jie，et al. Temperature effect on the impact of a liquid-jet against a rigid boundary[J].Optik，2013，124：1542-1546.

[4] 尹久红. 低压空化射流冲洗技术研究[D]. 成都：西南交通大学，2013.

[5] Jean-Pierre F，Michel R，Ayat K，et al. Material and velocity effects on cavitation erosion pitting[J].Wear，2012，274-275：248-259.

[6] Peng G Y，Shimizu Seiji. Progress in numerical simulation of cavitating water jets[J].Journal of Hydrodynamics，2013，25（4）：502-509.

[7] Reichardt H，Munzner H. Rotationally symmetric source-sink bodies with predominantly constant pressure distribution[J].Arm. Res. Est. Trans.，1975，1：1-7.

[8] Celik Arıkan Y，et al. Prediction of cavitation on two- and three-dimensional hydrofoils by an iterative BEM[C]//Proceedings of the 8th International Symposium on Cavitation，2012：696-702.

[9] Fahri Celik，Yasemin A O，Sakir Bal. Numerical simulation of flow around two- and three-dimensional partially cavitating hydrofoils[J].Ocean Engineering，2014，78：22-34.

[10] Bal S. Prediction of wave pattern and wave resistance of surface piercing bodies by a boundary element method[J].Numerical Methods in Fluids，2008，56 （3）：305-329.

[11] Bal S. The effect of finite depth on 2-D and 3-D cavitating hydrofoils[J].Journal of Marine Science and Technology，2011，16 （2）：129-142.

[12] Akira Sou，Barıs Bicer，Akio Tomiyama. Numerical simulation of incipient cavitation flow in a nozzle of fuel injector[J].Computers & Fluids，2014，103：42-48.

[13] Battistoni M，Grimaldi C N. Numerical analysis of injector flow and spray characteristics from diesel injectors using fossil and biodiesel fuels[J].Applied Energy，2012，97：656-666.

[14] Vijayakumar T，Thundil K R R，Nanthagopal K. Effect of the injection pressure on the internal flow characteristics for diethyl and dimethyl ether and diesel fuel injectors[J].Thermal Science，2011，15（4）：1123-1130.

[15] 王国玉，方韬，曹树良，等. 非定常黏性空化流动模型及其数值计算[J]. 工程热物理学报，2004，25：783-789.

[16] Tseng Chien-Chou，Wang Li-Jie. Investigations of empirical coefficients of cavitation and turbulence model through steady and unsteady turbulent cavitating flows[J].Computers & Fluids，2014，103：262-274.

[17] Singhal A K，Athavale M M，Li H Y，et al. Mathematical basis and validation of the full cavitation model[J].Journal of Fluid Engineering，2002，124：617-624.

[18] Saito Y，Nakamori I，Ikohagi T. Numerical analysis of unsteady vaporous cavitating flow around hydrofoil[C]//Fifth International Symposium on Cavitation，Osaka，Japan，2003.

[19] Owis F M，Nayfeh A H. Computation of the compressible multiphase flow over the cavitating high-speed torpedo[J].Journal of Fluid Engineering，2003，125（5）：459-468.

[20] Morgut M，Nobile E，Biluš I. Comparison of mass transfer models for the numerical prediction of sheet cavitation around a hydrofoil[J].International Journal of Multiphase Flow，2011，37（6）：620-626.

[21] Karim M M，Ahmmed M S. Numerical study of periodic cavitating flow around NACA0012 hydrofoil[J].Ocean Engineering，2012，55（1）：81-87.

[22] Vallier A，Nilsson H，Revstedt J. Mass transfer cavitation model with variable density of nuclei[C]//7th International Conference on Multiphase Flow，Tampa，USA，2010.

[23] Federico Brusiani，Stefania Falfari，Piero Pelloni. Influence of the diesel injector hole geometry on the flow conditions emerging from the nozzle[J].Energy Procedia，2014，45：749-758.

[24] Molina S，Salvador F J，Carreres M，et al. A computational investigation on the influence of the use of elliptical orifices on the inner nozzle flow and cavitation development in diesel injector nozzles[J].Energy Conversion and Management，2014，79：114-127.

[25] 钱忠东，黄社华. 四种湍流模型对空化流动模拟的比较[J]. 水科学进展，2006，17（2）：203-208.

[26] 卢义玉，王晓川，康勇，等. 缩放型喷嘴产生的空化射流流场数值模拟[J]. 中国石油大学学报：自然科学版，2009，3（6）：57-60.

[27] 刘思孝. 低压自激脉冲空化射流喷嘴内部流场的研究[D]. 济南：山东大学，2013.

[28] Asen P O，Kreiss G，Rempfer D. Direct numerical simulations of localized disturbances in pipe Poiseuille flow[J].Computers & Fluids，2010，39（6）：926-935.

[29] Martinez L，Benkenida A，Cuenot B. A model for the injection boundary conditions in the context of 3D simulation of diesel spray：Methodology and validation[J].Fuel，2010，89：219-228.

[30] Chesnel J，Reveillon J，Menard T，et al. Large eddy simulation of liquid jet atomization[J].Atomization Sprays，2012，21，711-736.

[31] Navarro-Martinez S. Large eddy simulation of spray atomization with a probability density function method[J].International Journal of Multiphase Flow，2014，63：11-22.

[32] Jiang X，Siamas G A，Jagus K，et al. Physical modelling and advanced simulations of gas-liquid two-phase jet flows in atomization and sprays[J].Progress in Energy and Combustion Science，2010，36：131-167.

[33] Chen Haosheng，Li Jiang，Chen Darong，et al. Damages on steel surface at the incubation stage of the vibration cavitation erosion in water[J].Wear，2008，265：692-698.

[34] 张晓东. 泄洪洞高速水流三维数值模拟[D]. 南京：中国水利水电科学研究院水力学所，2004.

[35] Li Songjing，Aung Nay Zar，Zhang Shengzhuo，et al. Experimental and numerical investigation of cavitation phenomenon in flapper-nozzle pilot stage of an electrohydraulic servo-valve[J].Computers & Fluids，2013，88：590-598.

[36] Postrioti Lucio，Malaguti Simone，Bo Si Maurizio，et al. Experimental and numerical characterization of a direct solenoid actuation injector for diesel engine applications[J].Fuel，2014，118：316-328.

[37] Man Z A，Yang W，Yao X. Numerical simulation of underwater contact explosion[J].Applied Ocean Research，2012，34：10-20.

[38] Miller S T，Jasak H，Boger D A，et al. A pressure-based，compressible，two-phase flow finite volume method for underwater explosions[J].Computers & Fluids，2013，87：132-143.

[39] Wu Z D，Sun L，Zong Z. Computational investigation of the mitigation of an underwater explosion[J].Acta Mechanica，2013，224（12）：3159-3175.

[40] Xie W F，Liu T G，Khoo B C. The simulation of cavitating flows induced by underwater shock and free surface interaction[J].Applied Numerical Mathematics，2007，57（5）：734-745.

[41] Wang Gaohui，Zhang Sherong，Yu Mao，et al. Investigation of the shock wave propagation characteristics and cavitation effects of underwater explosion near boundaries[J].Applied Ocean Research，2014，46：40-53.

[42] Kunz R F，Boger D A，Stinebring D R，et al. A preconditioned Navier-Stokes method for two-phase flows with application to cavitation prediction[J].Computers and Fluids，2000，29（8）：849-875.

[43] Lauer E，Hu X Y，Hickel S，et al. Numerical modelling and investigation of symmetric and asymmetric cavitation bubble dynamics[J].Computer & Fluids，2012，69：1-19.

[44] Sang J A，Oh J K. Numerical investigation of cavitating flows for marine propulsors using an unstructured mesh technique[J].International Journal of Heat and Fluid Flow，2013，43：259-267.

[45] Wang Yue，Qiu Lu，Reitz Rolf D，et al. Simulating cavitating liquid jets using a compressible and equilibrium two-phase flow solver[J].International Journal of Multiphase Flow，2014，63：52-67.

[46] Echouchene F，Belmabrouk H，Le Penven L，et al. Numerical simulation of wall roughness effects in cavitating flow[J].International Journal of Heat and Fluid Flow，2011，32：1068-1075.

[47] 邓松圣，沈银华，李赵杰，等. 空化射流喷嘴流场的数值模拟[J]. 后勤工程学院学报，2008，24（2）：42-46.

[48] He Zhixia，Zhong Wenjun，Wang Qian，et al. Effect of nozzle geometrical and dynamic factors on cavitating and turbulent flow in a diesel multi-hole injector nozzle[J].International Journal of Thermal Sciences，2013，70：132-143.

[49] Salvador F J，Martínez-López J，Romero J V，et al. Influence of biofuels on the internal flow in diesel injector nozzles[J].Mathematical and Computer Modeling，2011，54：1699-1705.

[50] Wang Xiang，Su Wanhua. Numerical investigation on relationship between injection pressure fluctuations and unsteady cavitation processes inside high-pressure diesel nozzle holes[J].Fuel，2010，89：2252-2259.

[51] Mohammad T S T，Soran P，Morteza G. Numerical study on the effect of the cavitation phenomenon on the characteristics of fuel spray[J].Mathematical and Computer Modeling，2012，56：105-117.

[52] Takakuwa O，Soyama H. The effect of scanning pitch of nozzle for a cavitating jet during overlapping peening treatment[J].Surface and Coatings Technology，2012，206：4756-4762.

[53] Soyama H. Effect of nozzle geometry on a standard cavitation erosion test using a cavitating jet[J].Wear，2013，297：895-902.

[54] Tzanakis I，Eskin D G，Georgoulas A，et al. Incubation pit analysis and calculation of the hydrodynamic impact pressure from the implosion of an acoustic cavitation bubble[J].Ultrasonics Sonochemistry，2014，21：866-878.

[55] Dabiri S，Sirignano W A，Joseph D D. Interaction between a cavitation bubble and shear flow[J].Journal of Fluid Mechanics，2010，651：93-116.

[56] Hsu Ching-Yu，Liang Cho-Chung，Teng Tso-Liang，et al. A numerical study on high-speed water jet impact[J].Ocean Engineering，2013，72：98-106.

[57] Guha Anirban，Barron Ronald M，Balachandar Ram. An experimental and numerical study of water jet cleaning process[J].Journal of Materials Processing Technology，2011，211：610-618.