定量结构-性质关系在化合物溶解度预测中的研究进展
2015-08-19孙飞飞雷乐成朱京科
孙飞飞,雷乐成,朱京科
(浙江大学化学工程与生物工程学院,生物质化工教育部重点试验室,浙江 杭州310027)
溶解度是化合物的一种基本性质,由化合物的分子结构所决定,在化工过程、药物和环境中化学物质迁移等研究方面都具有重要作用,因此建立快捷、可靠、普适的溶解度预测方法引起了人们极大兴趣。自20世纪70年代后,研究者们相继提出各种理论模型预测溶解度。1975年,Amidon等[1]基于分子表面积法建立理论模型,用于预测158个有机化合物的溶解度。之后,研究者们又相继提出了基团贡献法[2]、分子连接性指数法[3]以及人工神经网络法[4]等方法。此类方法均可归结为定量结构-性质构效关系(QSPR)方法,即根据化合物的分子结构参数(分子描述符)与某一性质(如溶解度)之间的定量关系建立预测模型。进行溶解度的QSPR研究主要包括两大步骤:①分子描述符的计算与优化;②模型的建立与评价。分子描述符通常根据所解决的问题从化合物的一系列理化参数中筛选,针对化合物溶解度的预测问题,研究者们相继提出了3类分子描述符:①组成描述符;②试验参数;③理论计算描述符。而相关的建模方法主要有:①线性建模法;②非线性建模法;③线性与非线性联合建模法。本文基于文献报道的溶解度预测方法的研究进展,分别评述了三类分子描述符所具有的特点,并介绍了三类最常用的建模方法,最后归纳总结溶解度预测方法所面临的挑战,并展望其未来发展趋势。
1 分子描述符
分子描述符是指分子在某一方面性质的度量,既可以是分子的物理化学性质,也可以是根据分子结构通过各种算法计算的数值指标[5-6]。这些性质可分为宏观与微观两类:前者包括化合物沸点、熔点、折光率和脂水分配系数(Kow)等,后者涉及分子尺寸形貌、偶极矩、分子能量、键能及氢键等。
1.1 组成描述符
此类描述符主要是基于基团贡献法计算得到的描述符,主要有:分子中各类原子、片段、指纹和化学键的相对或绝对数目、分子量、不同类型的环数等。在总结前人的基础上,Klopman等[7]提出了一套较为全面的包括118个官能团的描述符体系,包括52个常见的基本组成参数以及66个通过CASE法找出的额外组成参数,并应用于1168个化合物的溶解度预测[决定系数(R2)=0.95,标准偏差(SD)=0.50],证明了这组描述符能够较好地表达化合物分子结构。基团组成描述符计算简单,且无需借助其他理论计算方法,因而成为溶解度预测研究中最常使用的一类描述符。但基团贡献法不能反映化合物整体分子结构信息。
1.2 试验参数
试验参数指由试验测定的一类参数,与溶解度相关的经验描述符主要是化合物分子的集合性质,如Kow、熔沸点和折射率等。而Kow是化合物在水和辛醇中溶解能力的反映,与溶解度存在最直接的关系。如2001年,Jain和Yalkowsky[8]首次提出只包含Kow和熔点(Tm)两个参数的GSE方程(general solubilityequation)预测580个化合物溶解度,其预测结果的平均绝对误差值(AUE)达到0.42,具有很好的预测效果。然而,这类参数通常需要试验测定,相比与测定溶解度并未简化。
1.3 理论计算描述符
理论计算描述符指一类无需借助于试验测定,只需根据分子的结构信息就能计算得到的参数。随着计算机技术的发展,Dragon、MOE、Cerius2等软件包可计算得到近5000个涵盖化合物分子的电子结构(如分子轨道、键能及电荷分布等)与空间结构(分子拓扑结构、几何构象等)各类理化参数,原则上均可作为分子描述符。理论计算描述符对化合物结构描述全面,物化意义明确,理论性较强。
由软件计算得到的此类描述符数量众多,若全部用于建模将导致计算量大且模型不稳定,因此利用理论计算描述符建模必须先进行变量筛选。目前,常见的变量筛选方法主要有逐步回归法(SRM)、遗传算法(GA)以及替换法(RM)等[9]。目前在QSPR研究中,SRM是使用最多的一种变量筛选方法,Jiao等[10]利用SRM筛选出11个描述符建立模型,成功预测了23个二英类物质溶解度值[R2=0.9753,均方根误差(RMSE)=0.041]。尽管该方法简单易于实现,但该方法并不适用于大量的分子描述符量筛选。1992年Leardi等[11]提出用于变量筛选的GA法,之后GA在解决溶解度预测问题上得到了广泛应用。如Yin等[12]利用GA挑选出3个理论计算描述符(范德华面积,羧基中碳氧原子上电荷之和,溶质溶剂最高最低能级差),建立了71个含硫芳香酯溶解度的QSPR模型[R2=0.92,预测残差平方和(PRESS)=13.18]。与逐步回归法相比,GA适用范围更广。2008年Duchowicz等[13]首次提出了RM法,并成功运用该方法从Dragon计算的1497个分子描述符筛选出3个(X1sol、MLOGP、RDF060u)建立了预测145个药物溶解度的QSPR模型(R2=0.76,RMSE=1.2)。与GA相比,基于两种方法建立的模型精度相当,但RM法计算量较小。
对比三类分子描述符可知,从参数获得难易角度,组成描述符计算量小,最易获得,而试验参数需通过试验测定,涉及多种复杂测试方法,工作量大。理论计算描述符参数众多,需要对参数进行优化,计算量较组成描述符更大;从参数准确性角度,试验参数直接由试验测定,而组成描述符和理论计算描述符均通过分子结构信息计算得到,因此试验参数的准确性明显优于另两种描述符;从参数全面性角度考虑,理论计算描述符包含各类理化参数,对化合物结构的描述更全面细致,理论性更强。而试验参数需通过试验测定,对不易获得的化合物,无法得到相应试验参数。组成描述符通常伴有成分缺失问题,因而不能很好地表达化合物整体分子结构信息。由此可见,描述分子结构的三类描述符各有其优缺点,在溶解度的QSPR研究中,应根据具体情况选择描述符。
2 建模方法
目前在溶解度的QSPR研究中,已发展了各种建模方法,一般可分为线性和非线性模型,或是线性和非线性方法的组合。可用各种统计软件来实现建 模,如SPSS[14],SAS[15],Matlab[16]和STATISTICA[17]等。
2.1 线性方法
常见溶解度预测的线性方法有偏最小二乘法(PLS)、主成分回归(PCR)以及多元线性回归法(MLR)等。PLS法是通过同时考虑分子描述符X与溶解度Y并折衷各自空间内的因子,从而建立能够同时描述两者的模型,尤其适合溶解度样本较少的情况。潘善飞等[18]采用PLS法对84个有机物在离子液体中的溶解度进行QSPR研究(R2=0.98,SD=0.17),获得了很好的预测效果。PCR法是通过主成分分析法(PCA)从计算得到的大量分子描述符中选取对溶解度影响最大的几个主成分以建立相应的QSPR模型。
MLR法是建立多个分子描述符X与溶解度Y之间的关系,并为进一步了解影响化合物溶解度的本质因素提供有用信息,因此MLR法是使用最广泛的建立溶解度预测模型的方法[6]。王振东等[19]基于分子连接性指数建立了MLR模型,对卤代烷、环烷烃、烷基苯和卤代苯等有机污染物的溶解度进行预测,结果表明该模型具有良好的预测能力(R2=0.99)。Hewitt等[20]建立了基于理论计算描述符MLR模型,并对139个化合物进行了溶解度预测(R2=0.74,均方根误差RMSE=0.95),其预测结果表明:对于溶解度预测,MLR法要优于其他更复杂的建模方法。2001年,Yalkowsky等[8]建立了基于经验描述符Kow和Tm的MLR模型,如式(1)。

式(1)(即GSE方程)预测溶解度时需要试验值Kow和Tm,实际应用中具有局限性。近年来,一些研究者对GSE方程作了改进,提出用其他变量来替换Tm,即EGSE方程[21-22]。尽管近年EGSE方程不断改进,但仍未完全避免使用试验值,尤其对于较难获得的化合物,因得不到Kow值而不能预测相应的溶解度。
采用线性方法建立溶解度预测模型,过程较为简单,但比较适用于处理简单体系、样本量少的情况,且体系干扰严重时,易导致模型失真。
2.2 非线性方法
化合物溶解度与分子结构之间关系复杂,采用线性法建立的QSPR模型往往过于简单,模型的预测精度通常不及非线性方法建立的模型。Wang等[6]总结了近年来建立的溶解度预测模型,发现非线性方法的预测精度通常优于线性方法。近年来计算机技术的不断成熟使得基于“机器学习”的非线性建模方法得以飞速发展,目前常用的非线性建模方法主要有人工神经网络(ANN)、支持向量机(SVM)以及高斯过程(GP)等。
ANN是由数目众多、功能相对简单的神经元相互连接而成的复杂非线性系统,在溶解度预测领域,其地位仅次于MLR[6]。由于其吸取了生物神经网络的许多特点,因而具有较强的非线性映射能力、容错性、自学习和自适应能力。此外还兼有动态、处理模糊信息和不连续数值等特点[23]。人工神经网络的种类繁多,其中在溶解度预测领域,前馈神经网络(FFNN)使用最为广泛,其基本结构如图1所示[24]。网络的输入层接收外部信号,其神经元个数对应于输入参数的个数;一个神经元的输出层对应化合物溶解度;隐含层个数则根据具体情况优化得到。Farhad等[25]建立了基于基团组成描述符的ANN模型,成功预测了室温下3585个有机化合物在水溶液中的溶解度(R2=0.86,RMSE=0.4)。Piliszek等[26]以GA优化后的理论计算描述符,建立了预测209个偶氮苯溶解度的ANN模型(R2>0.9,RMSE<0.6)。
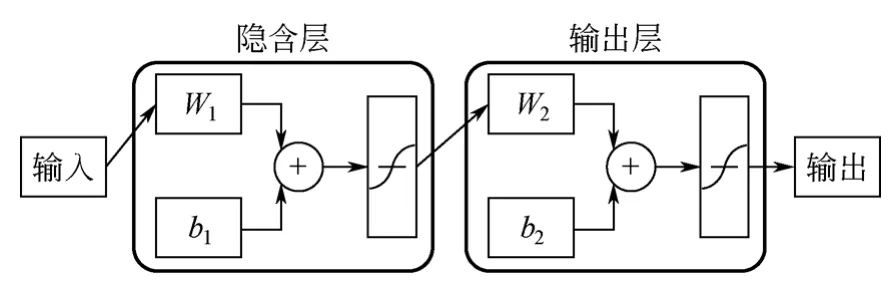
图1 关联预测化合物溶解度的FFNN结构
近年来,SVM作为一种由机器学习算法发展的新算法在关于溶解度QSPR研究领域引起人们广泛的关注。兰州大学刘满仓教授课题组[27]基于理论计算描述符,运用SVM方法建立了溶解度预测模型,成功预测了217个烃类化合物在饱和盐水中的溶解度(R2=0.987,RMSE=0.192),同时还阐明了与烃类化合物溶解度相关的结构特征以及验证了SVM方法的灵活性。此外,GP作为一种新近提出的QSPR研究方法,目前也被用来构建溶解度预测模型。如Rostami等[28]成功运用GP建立了关于原油中沥青的溶解度预测模型(RMSE=0.37),并通过比较表明该模型预测精度优于之前的模型。
与线性建模方法相比,非线性方法建立溶解度预测模型具有一定优势,其适用范围广,预测精度高,具有容错性、自适性等优点,但该方法也存在不足之处:第一,非线性方法建模类似于“黑箱”操作,无法像线性建模法一样得到明确的输入输出关系;第二,若样本量过少,易造成过拟合;第三,结果重复性不如线性方法。
2.3 线性与非线性方法联用
在QSPR研究中,尽管使用线性或非线性建模法建立的溶解度预测模型已达到较好的预测精度,但近年发展的线性与非线性结合方法具有更好的建模结果。使用较多的是先利用线性法筛选出分子描述符的最优子集,然后以该最优子集为输入变量建立非线性模型。GA-MLR和ANN联用建模是一种典型的方式,其中GA-MLR主要用于筛选最优子集表达化合物分子结构,而ANN则以该最优子集为输入参数,样本溶解度值为输出变量建立QSPR模型。如Gharagheizi等[29]利用GA-MLR从Dragon软件计算的1259个分子描述符中筛选出5个分子描述符表达溶剂分子结构,以此为基础构建的ANN模型成功预测了富勒烯在128种不同溶剂中的溶解度(R2=0.943,RMSE=0.071)。PLS和PCR等线性建模方法也被用来筛选分子描述符,与非线性建模方法联用建模。如Liu等[30]利用主成分分析法找出与溶解度最相关的主成分,并以此作为ANN模型的输入,达到了很好的预测效果(R2=0.90,RMSE=0.68)。
此外,Hansen等[31]则基于HH方程[32](Henderson-Hasselbalchequation)提出了线性和非线性组合方法预测有机化合物在不同pH值水溶液中的溶解度。针对4548个有机化合物,该方法首先分别建立分子结构与本征溶解度及与化合物酸解离系数pKa的非线性QSPR模型(RMSE分别为0.7和0.71),然后根据线性的HH方程预测不同pH值水溶液中化合物的溶解度。经已知27个化合物不同pH值的溶解度数据验证,预测精度RMSE达到0.79。
线性和非线性组合方法更适合复杂问题,能处理前两类方法无法直接使用的体系。具有拟合能力强的明显优势,但是由于同时采用两类方法,一般模型拥有相对较多的参数,更易过拟合,尤其在两类方法的偏差存在叠加效应时,容易产生较大的预测误差。
3 溶解度预测模型的发展
随着QSPR研究溶解度的不断深入,相应建立的溶解度预测模型也发生变化。2004年之后,研究者们普遍倾向于研究大量化合物在室温、纯水中的溶解度。如Wang等[33]建立了以基团组成描述符为输入的溶解度预测模型,很好地预测了3664个化合物的水溶液中的溶解度(AUE=0.631,RMSE=0.850),并将该模型用于预测Huuskonen报道的溶解度值[34],也达到了较好的预测效果(AUE=0.54,RMSE=0.72)。而近两三年来,研究者们逐渐开始考虑化合物在pH值、温度、溶剂等外在条件参数改变时的溶解度值(即表观溶解度)。如Valenzuela等[35]研究了30个化合物在超临界CO2中的溶解度并建立了相应的QSPR模型(R2>0.91)。
尽管目前已经报道过的一些溶解度预测模型具有不错的预测精度,但是关于溶解度的QSPR研究,依旧任重而道远。Hewitt等[20]通过32个已知溶解度的化合物对自己建立的MLR、ANN等溶解度预测模型以及其他一些商业来源的预测模型进行评估,这些模型的RMSE值在0.82~1.56,且模型的平均预测误差达到1.1(lgS)。说明目前进行溶解度预测仍旧面临巨大挑战。总结报道的溶解度预测模型不难看出,关于室温水溶液中溶解度的QSPR研究日趋成熟,而由于化合物表观溶解度很难获得,因此目前关于化合物的表观溶解度值及其变化情况的QSPR研究较少,且涉及的化合物种类单一。
4 展望
随着近年来计算机技术的飞速发展,研究者们依托编程及软件开发提出大量用于预测化合物溶解度的模型,这些模型的建立除了对化合物溶解度的预测具有指导性意义外,同时对了解化合物分子结构与溶解度之间的关系也提供了一定参考。目前,关于溶解度的QSPR研究仍存在不足,如何提高溶解度预测模型的预测精确是未来仍需解决的问题。此外,研究者们将更关注不同pH值、温度、溶剂等条件下化合物分子结构与溶解度的构效关系。为此,在未来的溶解度预测模型建立过程中,从数据采集、描述符计算和筛选、模型方法的选择及建立,到模型的验证每一个建模步骤都需要采取恰当的措施加以改进,以提高最终建立模型的预测可靠性。
[1]Amidon G,Yalkowsky S,Anik S,etal.Solubility of nonelectrolytes in polar solvents.V.Estimation of the solubility of aliphatic monofunctional compounds in water using amolecular surface area approach[J].TheJournalofPhysicalChemistry,1975,79(21):2239-2246.
[2]van Krevelen D W.Properties of Polymers:Their Estimation and Correlation w ith Chem ical Structure[M].Amsterdam:Elsevier Scientific Publ.,1976.
[3]Bicerano J.Prediction of Polymer Properties[M].New York:Marcel Dekker,1993.
[4]Ebube N K,Owusu-Ababio G,Adeyeye CM.Preformulation studies and characterization of the physicochem ical properties of amorphous polymers using artificial neural networks[J].InternationalJournalof Pharmaceutics,2000,196(1):27-35.
[5]任伟,孔德信.定量构效关系研究中分子描述符的相关性[J].计算机与应用化学,2009(11):1455-1458.
[6]Wang J,Hou T.Recentadvances on aqueous solubility prediction[J].CombinatorialChemistry&HighThroughputScreening,2011,14(5):328-338.
[7]Klopman G,Zhu H.Estimation of the aqueous solubility of organic molecules by the group contribution approach[J].Journalof ChemicalInformationandComputerSciences,2001,41(2):439-445.
[8]Jain N,Yalkowsky SH.Estimation of the aqueous solubilityⅠ:Application to organic nonelectrolytes[J].JournalofPharmaceutical Sciences,2001,90(2):234-252.
[9]Jouyban A,Shayanfar A,Ghafourian T,etal.Solubility prediction of pharmaceuticals in dioxane+waterm ixtures at various temperatures:Effects of different descriptors and feature selection methods[J].JournalofMolecularLiquids,2014,195:125-131.
[10]Jiao L,LiH.QSPR studieson theaqueous solubility of PCDD/Fsby using artificial neural network combined w ith stepw ise regression[J].ChemometricsandIntelligentLaboratorySystems,2010,103(2):90-95.
[11]LeardiR,Boggia R,Terrile M.Genetic algorithms as a strategy for feature selection[J].JournalofChemometrics,1992,6(5):267-281.
[12]Yin C,Liu X,GuoW,etal.Prediction and application in QSPR of aqueous solubility of sulfur-containing aromatic esters using GA-based MLRwith quantum descriptors[J].WaterResearch,2002,36(12):2975-2982.
[13]Duchow icz PR,TaleviA,Bruno-Blanch LE,etal.New QSPR study for the prediction of aqueous solubility of drug-like compounds[J].Bioorganic&MedicinalChemistry,2008,16(17):7944-7955.
[14]Norušis Marija J.SPSS Inc.SPSS Professional Statistics 6.1[M].Prentice Hall,1994.
[15]SASVisualAnalytics6.1:User’sGuide[M].Sas Institute,2012.
[16]GuideM U.TheMathworks[M].Inc.,Natick,MA,1998.
[17]StatSoftH.Statistica 6[M].Springer,2002.
[18]潘善飞,胡桂香,吕杨,等.离子液体中有机物溶解度的QSPR模型分析[J].物理化学学报,2010,26(9):2494-2502.
[19]王振东,杨锋,周培疆.分子连接性指数对部分有机污染物溶解度及疏水参数的预测[J].环境化学,2003,22(4):380-384.
[20]Hew itt M,Cronin M T,Enoch S J,et al.In silico prediction of aqueous solubility:The solubility challenge[J].JournalofChemical InformationandModeling,2009,49(11):2572-2587.
[21]Hughes LD,Palmer D S,Nigsch F,etal.Why are some properties more difficult to predict than others?A study of QSPR models of solubility,melting point,and Log P[J].JournalofChemical InformationandModeling,2008,48(1):220-232.
[22]Zhou D,Alelyunas Y,Liu R.Scores of extended connectivity fingerprintas descriptors in QSPR study ofmelting pointand aqueous solubility[J].JournalofChemicalInformationandModeling,2008,48(5):981-987.
[23]王洪元,史国栋.人工神经网络技术及其应用[M].北京:中国石化出版社,2002.
[24]Mehrpooya M,MohammadiA H,Richon D.Extension of an artificial neural network algorithm for estimating sulfur content of sour gases at elevated temperatures and pressures[J].Industrial&Engineering ChemistryResearch,2009,49(1):439-442.
[25]Gharagheizi F,Eslam imanesh A,Mohammadi A H,et al.Representation/prediction of solubilities of pure compounds in water using artificial neural network——Group contribution method[J].JournalofChemical&EngineeringData,2011,56(4):720-726.
[26]Wilczyńska Piliszek A J,Piliszek S,Falandysz J.QSAR and ANN for the estimation of water solubility of 209 polychlorinated trans-azobenzenes[J].JournalofEnvironmentalScienceandHealth,PartA,2012,47(2):155-166.
[27]马卫平.线性和非线性方法在QSAR/QSPR研究中的应用[D].兰州:兰州大学,2007.
[28]Rostam i H,Khaksar Manshad A.Prediction of asphaltene precipitation in live and tank crude oil using gaussian process regression[J].PetroleumScienceandTechnology,2013,31(9):913-922.
[29]Gharagheizi F,Alamdari R F.A molecular‐based model for prediction of solubility of C60 fullerene in various solvents[J].Fullerenes,Nanotubes,andCarbonNonstructures,2008,16(1):40-57.
[30]Liu Y,Sun X,Ouyang A.Nondestructivemeasurement of soluble solid content of navel orange fruit by visible-NIR spectrometric technique w ith PLSR and PCA-BPNN[J].LWT-FoodScienceand Technology,2010,43(4):602-607.
[31]Hansen N T,Kouskoumvekaki I,Jørgensen FS,etal.Prediction of pH-dependent aqueous solubility of druglikemolecules[J].Journalof ChemicalInformationandModeling,2006,46(6):2601-2609.
[32]Hasselbalch K.Calculation of blood pH based on the free and bound carbonic acid,and oxygen binding of blood as function of pH[J].Die Biochem.Z,1916,78:112-144.
[33]Wang J,Hou T,Xu X.Aqueous solubility prediction based on weighted atom type counts and solvent accessible surface areas[J].JournalofChemicalInformationandModeling,2009,49(3):571-581.
[34]Huuskonen J,Rantanen J,Livingstone D.Prediction of aqueous solubility for a diverse set of organic compounds based on atom-type electrotopological state indices[J].EuropeanJournalofMedicinal Chemistry,2000,35(12):1081-1088.
[35]Valenzuela LM,Reveco A,del Valle JM.Modelling solubility in supercritical carbon dioxide using quantitative structure-property relationships[J].TheJournalofSupercriticalFluids,2014,94(10):113-122.
