种群分布式并行遗传算法解化工多目标优化问题

潘欣，刘海燕，廖安，鄢烈祥，史彬

（武汉理工大学化学化工与生命科学学院，湖北 武汉430070）

化工行业中的优化问题经常需同时考虑产量、耗量费用、污染排放等[1]多个目标，而这多个目标间往往相互矛盾，一个目标的改善有可能会引起另一个或者另几个目标的性能降低，也就是要同时使多个目标一起达到最优值是不可能的。这时就需对各个目标进行协调，找到一个使各个目标都尽可能达到最优的解的集合以供决策者选择。非支配解集（Pareto解集）经常被用来解决这类多目标问题，其特点是集合中的每个解都至少存在一个目标优于其他所有的解，这样一个多目标优化问题就被转化为一个非支配解集的求解问题。进化算法（evolutionaryalgorithm，EA）作为一类启发式搜索算法，已被成功应用于多目标优化领域，它通过维持代与代之间由潜在解组成的种群来实现全局搜索，能有效提高非支配解的搜索效率[2]。

第一代多目标进化算法始于20世纪90年代初，以MOGA（multi-objectivegeneticalgorithm）[3]和NSGA（non-dominatedsortinggeneticalgorithm）[4]等为代表，其特点是采用了基于Pareto等级的个体选择方法和基于适应度共享机制的种群多样性保持策略。与第一代进化算法相比，以Zitzler等[5]提出的SPEA（strengthParetoevolutionaryalgorithm）和Knowles等[6]提出的PAES（Paretoarchived evolutionstrategy）等为代表的第二代进化算法[7]引入了精英保留机制，避免了优秀解在下一代进化过程中被破坏。目前，第二代进化算法已被普遍应用于各行各业的优化中，其中以Deb等[8]学者通过对非支配排序遗传算法进行改进提出的NSGA-Ⅱ最具代表性。NSGA-Ⅱ算法降低了非劣排序遗传算法的复杂性，具有运行速度快，解集的收敛性好等优点，是目前最流行的多目标优化算法之一。

近年，有国内外学者将PAES、NSGA、SPEA等进化算法应用到化工领域解决各类问题，这其中以其与流程模拟软件相结合的优化研究较多[9-11]。以AspenPlus软件为例，因其具有完备的物性数据库和强大的模型分析工具，可以对工况数据进行较准确的模拟。然而，当需要模拟的流程较为复杂或者含有循环流股时，模拟耗时较长且不易收敛，流程模拟软件与进化算法相结合优化的计算效率不高。为了解决这一问题，本文引入了一种多目标并行计算方法PDPGA，对遗传算法的子代种群进行分组，利用局域网的多台子节点计算机同时调用AspenPlus软件对子种群进行模拟计算，降低串行优化的耗时以达到降低总体模拟时间，提高优化效率的目的。

1 种群分布式并行遗传算法

1.1 遗传算法的并行化

遗传算法最初由美国Michigan大学J.Holland教授于1975年首先提出，是一种通过模拟自然进化过程搜索最优解的方法。但随着科学技术的发展，问题的规模不断扩大和复杂度难度增加，对遗传算法求解质量和运行速度都提出了更高的要求，经典串行遗传算法的搜索时间会被成倍地延长。很多学者都致力于提高遗传算法的搜索效率，一个重要的研究方向就是遗传算法的并行化[12-13]。目前主要有4种并行化模型：主从式模型、粗粒度模型、细粒度模型和混合模型。相比于后3种复杂的并行化模型，主从式模型[14]不改变遗传算法的基本结构特点，只有一个群体而且全部都在统一的环境中进化，只将适应度评价部分并行化执行，是一种直接的并行化方案，对于适应度计算过程耗时长的优化过程尤其适用。本文提出的PDPGA算法采用的就是主从式模型。

1.2 PDPGA优化策略

PDPGA算法是一种基于种群的分布式并行遗传算法，该方法以NSGA-II算法为框架，采用主从节点分布的策略。主节点的负责初始化种群，对父代进行选择、交叉和变异产生子代，并对子代种群进行分组和结果回收。子节点的作用是接收主节点分配子代种群，计算其目标值，并返回给主节点。

PDPGA算法具体步骤如下所述。

（1）主节点初始化种群P0，对其进行非支配排序得到其Pareto最优解集Pt0。同时建立一个外部保留种群Pt，将Pt0保存至外部保留种群Pt中。

（2）主节点对P0进行选择、交叉和变异，产生子代种群Pc（不计算其目标值）。对产生的子代种群进行分组，即Pc={Pc1，Pc2，…，Pcn}，其中n为局域网中的计算机台数。

（3）将Pc1，Pc2，…，Pcn分别发送给n台局域网的子节点计算机，各节点机计算其接收到种群的目标值（f1，f2，…，fn），计算完成后将目标值返回主节点。

（4）主节点收集子节点返回的目标值，合并Pc1和f1、Pc2和f2，…，Pcn和fn，并将合并后的n个子种群在进行合并，得到完整的子代种群P1。

（5）对P1进行非支配排序得到第一代进化的Pareto最优解集Pt1，将Pt1保存至外部保留种群Pt。在对外部保留种群Pt进行非支配排序删除其中的支配解，用得到的Pareto最优解集更新Pt。

（6）对P1重复步骤（2）、（3）和（4）的操作得到P2，对P2进行步骤（5）的操作得到Pt2和新的Pt，如此循环直到满足循环迭代的终止进化代数为止。最终所得的外部保留种群的Pareto最优解集Pt即为所求的多目标优化结果。

2 PDPGA与流程模拟软件结合优化

将模拟软件与遗传算法相结合优化时，可将模拟软件看成一个“黑箱”，用于计算相应参数下对应的目标值，属于适应度评价的计算部分，对其进行并行化求解符合主从式模型的应用特点。图1所示为PDPGA与AspenPlus软件结合优化的计算框图。与NSGA-II算法主要差别在于PDPGA算法对每次父代进行遗传、交叉和变异产生的子代进行了分组，分组后的子种群交由局域网的其他子节点计算机计算。各子节点计算机接收计算任务后，同时调用AspenPlus软件进行模拟计算，计算完成后将子节点的模拟结果收集反馈给主节点，主节点进行非支配排序及精英保留操作后进行下一代的进化。PDPGA通过将大量的模拟任务分配给不同的节点计算机同时计算，有效降低模拟过程在整个优化过程中的耗时，提高了优化效率。

应用PDPGA与AspenPlus结合进行优化时，数据通信主要发生在每一代的主节点将种群分配给子节点和子节点调用AspenPlus计算后将结果反馈给主节点这两部分。为降低局域网数据通信时间开销在整个优化过程中的耗时比例，在进化代数一定的情况下，应适当加大种群规模。考虑到变量的个数和遗传算法的特性，种群规模在60～200较好，每个子节点计算机分配到的子种群数控制在30～60为宜。

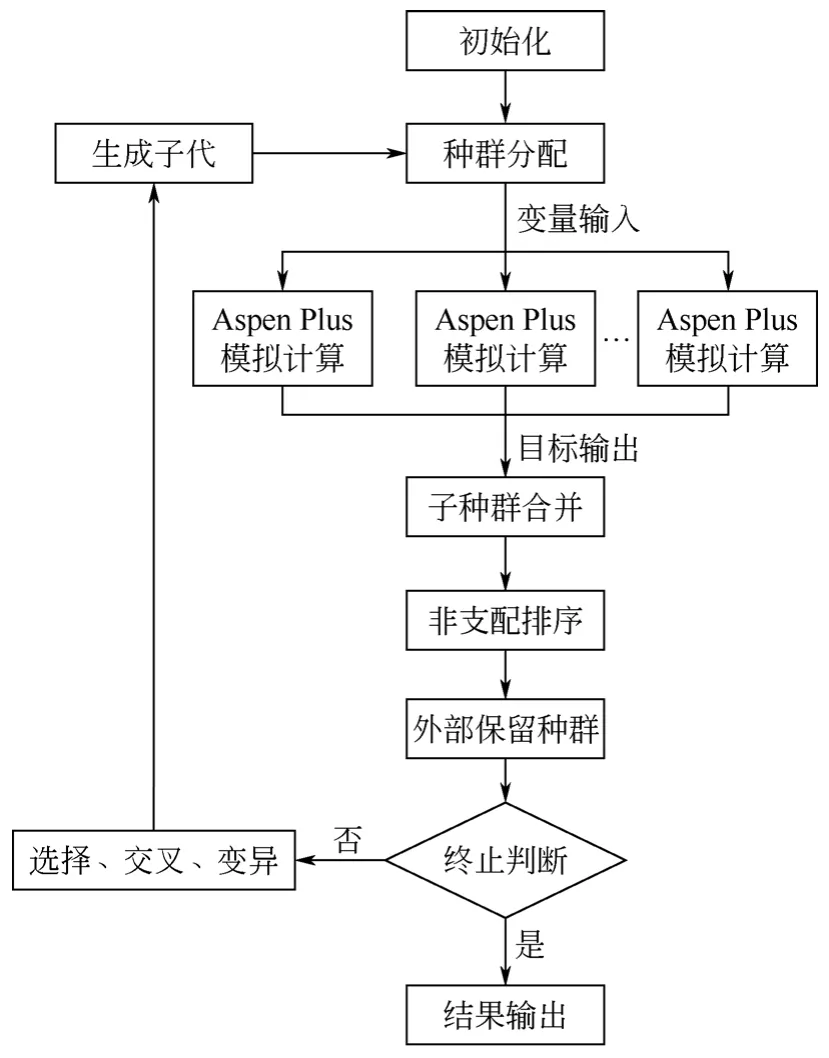
图1 PDPGA与AspenPlus结合计算框图

3 PDPGA优化氯乙烯精制两目标问题

氯乙烯（VCM）是一种应用于高分子化工的重要的单体，其聚合物聚氯乙烯（PVC）是日常生活中应用最广的一种塑料材料。目前，工业上生产氯乙烯的主要方法[15]有电石法和二氯乙烷裂解法，无论哪种方法生产的VCM都含有二氯乙烷、氯化氢、水等杂质，需要经过精馏过程将杂质除去，常用的方法是通过双塔精馏（低沸塔和高沸塔）分别除去杂质中的低沸物和高沸物组分以得到纯净的VCM单体[16]。

3.1 氯乙烯精制过程模拟

本文选择的氯乙烯精制工艺包括二氯乙烷（EDC）裂解生成粗VCM，以及粗VCM双塔精馏除去N2、C2H2和HCl等物质。本文首先模拟EDC裂解过程，然后选用文献[17]的工艺来模拟VCM精馏过程，整个过程的AspenPlus流程如图2。其中，裂解炉A1中的EDC的裂解率为55%，粗VCM精馏模拟的相关参数可参考文献[17]。模拟得到的低沸塔和高沸塔的能耗见表1，进料量及主要流股的模拟结果见表2。

表1 低沸塔和高沸塔能耗

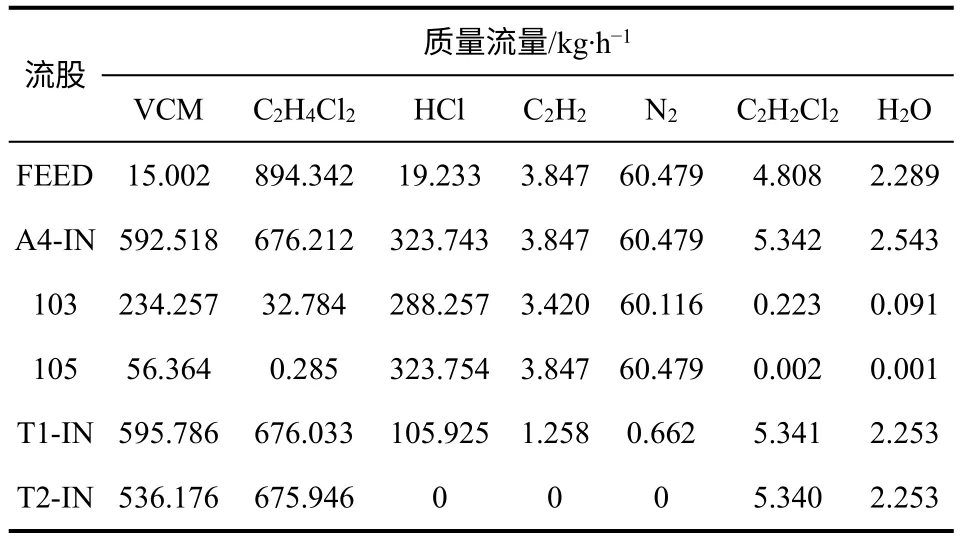
表2 模拟结果

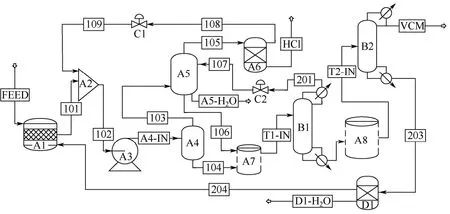
图2 氯乙烯精制过程模拟

3.2 氯乙烯精制优化过程数学模型建立

氯乙烯精制过程双目标优化的数学模型为式（1）。

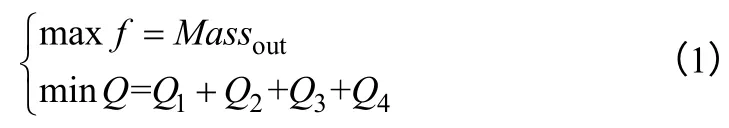
式中，f和Q为氯乙烯精制过程优化的双目标：①氯乙烯采出量最大化；②过程总能耗最小化。Massout表示高沸塔顶氯乙烯的质量采出量，kg/h；Q1、Q2、Q3、Q4分别为低沸塔和高沸塔的冷凝器和再沸器的能耗，Gcal/h。

变量范围与约束条件为：

式中，Φ表示氯乙烯精制过程满足的约束方程组，由AspenPlus模块来描述；优化变量有6个，其中x1、x2和x3分别表示低沸塔B1的馏出率、质量回流比和塔压，x4、x5和x6分别表示高沸塔B2的馏出率、质量回流比和塔压。模型的约束条件为：①氯乙烯产品质量分数x7达到要求；②模拟的结果中低沸塔和高沸塔模块的冷凝器及再沸器热负荷x8～x11不超过150Mcal/h。

3.3 优化结果比较和分析

分别应用NSGA-II和PDPGA与AspenPlus结合对上述过程优化，两种优化算法的种群规模均设为70，进化代数也为70。其中NSGA-II优化使用单台计算机串行计算，而PDPGA优化使用1个主节点计算机和2个从节点计算机并行计算（运行计算机CPU均为Corei5-34703.2GHz）。图3和图4分别为PDPGA和NSGA-II算法求得的氯乙烯采出量和系统总能耗双目标Pareto前沿。从图中可以看出，随着低沸塔和高沸塔的总能耗从0.2Gcal/h增加到0.25Gcal/h，氯乙烯的采出量会逐渐增加到530kg/h。进一步增加低沸塔和高沸塔的热负荷，氯乙烯的采出量将不再变化。

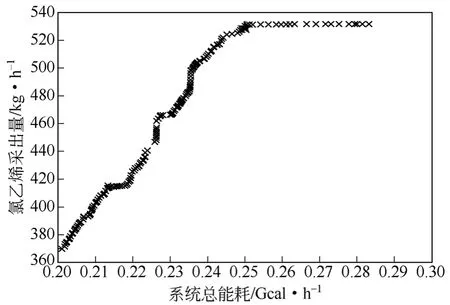
图3 PDPGA优化的Pareto解集

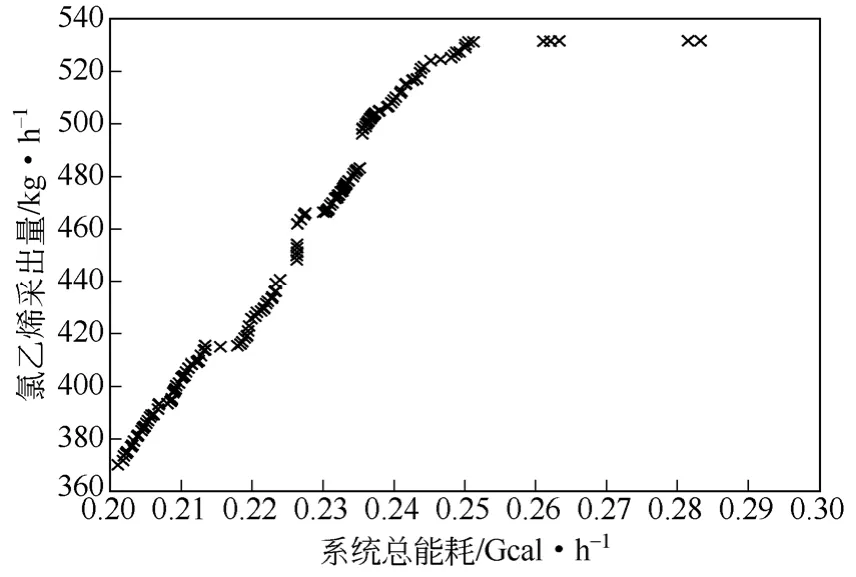
图4 NSGA-II优化的Pareto解集

图3中，“★”点为优化后选取的操作点，将其对应的优化变量和优化目标的取值与3.1节中模拟值的对比列于表3和表4。从表3中可以看出，通过适当降低低沸塔和高沸塔塔压，优化后的低沸塔馏出率和质量回流比均降低了30%左右，这就使得低沸塔的热负荷大幅下降；高沸塔的质量回流比大幅下降，有效较低了高沸塔的热负荷，同时提高馏出率有利于提高VCM的产量。

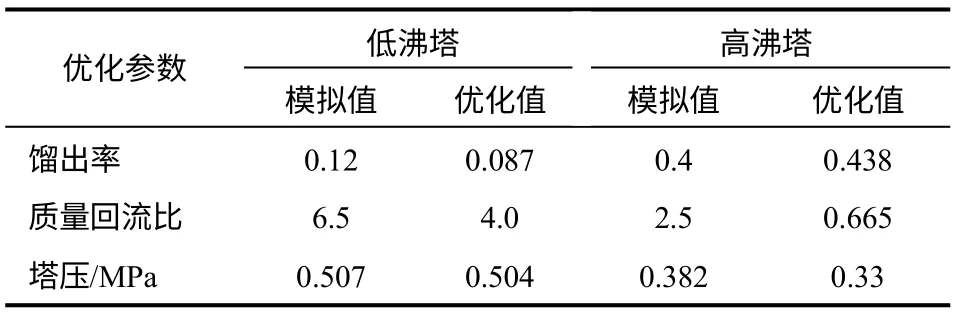
表3 优化变量的模拟值与优化值对比

表4 优化目标的模拟值与优化值对比

比较PDPGA和NSGA-Ⅱ二者的最优解集Pareto前沿可知，应用PDPGA优化所得的Pareto前沿分布的比应用NSGA-Ⅱ得到的Pareto前沿均匀。分布均匀的Pareto前沿有利于准确地反映多目标问题的各个子目标之间的制约关系，在实际工业应用中可以给决策者提供更多可供选择的操作点。表5给出了两种算法的优化性能比较，从表中可以看出，使用双节点计算机的PDPGA并行计算比单节点的NSGA-Ⅱ计算需多使用2台计算机，但优化时间节省近40%。而实验室和工厂中往往都有闲置计算机未使用，利用PDPGA算法优化能在不增加购买高速计算机成本的同时，通过有效利用闲置的计算机资源来降低计算所需时间。

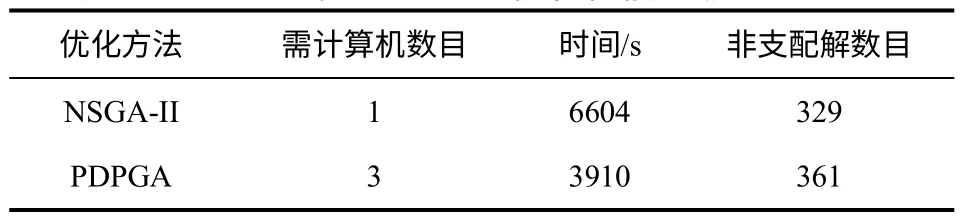
表5 PDPGA和NSGA-Ⅱ优化性能比较

4 结论

本文针对AspenPlus等流程模拟软件与遗传算法结合优化耗时较长的问题，提出了一种种群分布式并行遗传算法PDPGA。算法通过多台计算机并行计算，能有效降低流程模拟在整个优化过程中的时间消耗。将PDPGA应用于氯乙烯精制过程多目标优化的实例求解，并与传统NSGA-II算法直接进行优化相比较表明，使用基于种群分布式的并行遗传算法可以在更短的时间内，获得分布均匀且质量更好的Pareto解集。

[1]赵博，袁希钢，罗祎青.考虑环境影响的间歇过程多目标最优化设计[J].化工进展，2007，26（2）：113-118.

[2]公茂果，焦李成，杨咚咚，等.进化多目标优化算法研究[J].软件学报，2009，20（2）：271-289.

[3]Fonseca C M，Flem ing P J.Genetic algorithms formulti-objective optimization：Formulation discussion and generalization[J].ICGA，1993，93：416-423.

[4]Srinivas N，Deb K.Mutiobjective optim ization using non-dom inated sorting in genetic algorithms[J].EvolutionaryComputation，1994，2（3）：221-248.

[5]Zitzler E，Thiele L.Multi-objective evolutionary algorithms：A comparative case study and the strength Pareto approach[J].EvolutionaryComputation，1999，3（4）：257-271.

[6]Know les JD，Corne DW.Approximating the non-dominated front using the Pareto achived evolution strategy[J].Evolutionary Computation，2000，8（2）：149-172.

[7]Konak A，CoitDW，Sm ith A E.Multi-objective optim ization using genetic algorithms：A tutorial[J].ReliabilityEngineering&System Safety，2006，91（9）：992-1007.

[8]Deb K，Pratap A，Agarwal S，etal.A fastand elitistmultiobjective genetic algorithm：NSGA-II[J].EvolutionaryComputation，2002，6（2）：182-197.

[9]俞辉，王超，李丽娟，等.基于非支配排序遗传算法的乙苯脱氢工艺条件优化[J].化工学报，2012，63（9）：2771-2776.

[10]林子雄，鄢烈祥，李骁淳，等.基于流程模拟器和列队竞争算法的精馏操作优化[J].化工进展，2013，32（1）：54-58.

[11]Wang D，Feng X.Simulation andmulti-objective optim ization of an integrated process for hydrogen production from refinery off-gas[J].InternationalJournalofHydrogenEnergy，2013，38（29）：12968-12976.

[12]Luque G，Alba E.Natural Language Tagging w ith Parallel Genetic Algorithms[M].Berlin Heidelberg：Springer，2011：75-89.

[13]卢海，鄢烈祥，史彬，等.并行多家族遗传算法解多目标优化问题[J].化工学报，2013，64（12）：3985-3990.

[14]谢克家，刘昕，王成良，等.多核计算环境下改进的主从式并行遗传算法[J].微计算机信息，2011，27（3）：164-166.

[15]陈静，侯春阳，金炜阳，等.乙炔法生产氯乙烯工业反应技术研究进展[J].化工进展，2010，29（9）：1603-1608.

[16]张军.氯乙烯生产工艺中操作参数优化研究[D].上海：华东理工大学，2013.

[17]李群生，于颖，郭增昌.氯乙烯精馏工艺流程的模拟计算及技术改造[J].石油化工，2012（7）：820-824.