基于CART-LSSVM的球磨机料位软测量方法研究*

张　兴，李　伟，阎高伟*，庞宇松

（1.太原理工大学信息工程学院，太原030024 2.荷兰代尔夫特理工大学机械海运与材料工程学院，荷兰）

基于CART-LSSVM的球磨机料位软测量方法研究*

张兴1，李伟1，阎高伟1*，庞宇松2

（1.太原理工大学信息工程学院，太原030024 2.荷兰代尔夫特理工大学机械海运与材料工程学院，荷兰）

球磨机是用于电力、磨矿和冶金等行业的高能耗设备，准确测量其滚筒料位能够提高运行效率和安全性能。针对其滚筒内料位难以实时检测，球磨机的轴承振动信号中存在较多的冗余特征，提出了一种基于分类回归树和最小二乘支持向量机的软测量方法，首先用Welch法获得振动信号的功率谱密度，并分割得到基本特征，然后建立分类回归树模型，根据最优树模型的分支节点进行特征选择，最后利用最小二乘支持向量机实现特征变量与料位间的非线性映射。通过实验结果的对比分析，验证了该模型的有效性和实用性，以及良好的预测精度。

球磨机料位；软测量；特征选择；分类回归树；最小二乘支持向量机；振动信号

EEACC:7230doi:10.3969/j.issn.1004-1699.2015.09.016

滚筒式球磨机是一种用于磨矿及制粉工业等过程的主要设备，其工作过程是涉及破碎力学、机械振动与噪声学等多个学科的复杂过程，筒体振动信号存在冗余性和互补性［1］，且由于其封闭旋转运行的工作特性，球磨机料位参数与筒体振动信号的映射关系难以直接有效建立，因此经常会发生空磨、饱磨、堵磨等现象，从而影响生产效率或带来安全问题。因此需要准确可靠检测料位，使球磨机运行在最佳状态。

近年来，科研技术人员针对该问题提出了很多解决方法，其中以软测量方法为主要代表，其模型的基本结构为特征降维方法结合机器学习方法。文献［2］采用主成分分析［3］方法（Principal Component Analysis，PCA）提取振动功率谱特征，再采用支持向量机（Support Vector Machines，SVM）建立料位和频谱特征之间的关系模型。文献［4］采用主成分分析（Principle Component Analysis，PCA）方法进行振动信号的特征提取，然后采用偏最小二乘回归方法（Partial Least Square Regression，PLSR）建立料位软测量模型。文献［5］采用偏最小二乘法（Partial Least Square，PLS）进行振动信号的特征提取，然后采用极限学习机（Extreme Learning Machine，ELM）建立料位软测量模型。以上三种方法利用振动信号，均可以实现球磨机料位的软测量，但是存在降维后特征的维数难以有效准确确定的问题，通常需要反复试验确定一个较好的特征作为模型下一阶段输入。文献［6］采用自适应遗传算法—偏最小二乘法（Adaptive Genetic Algorithm-Partial Least Squares，AGA-PLS）选择频谱特征，然后融合时域电流信号，基于PLS算法建立融合时频数据特征的球磨机料位软测量模型，其特征选择过程结合了自适应遗传算法（AGA），时间复杂度有所上升。

为此，本文结合分类回归树和最小二乘支持向量机，并将该方法用于基于球磨机轴承振动信号的料位软测量建模。实验结果表明，该方法避免了复杂的特征提取及维数选择过程，具有较好的测量精度及稳定性，为软测量建模中数据的降维提供了一种新思路。

分类回归树［7］（Classification and Regression Tree，CART）为一种基于统计分析的非参数识别技术，具有多元参数、非参数统计等优点，利用其较高的分类正确率［8］，CART能自动进行特征选择，有效降低变量维数。这种特征选择的方法有以下几个优点:①能简单高效地处理高维特征；②为一个非参数过程，不依赖于特定的函数形式；③树的分支节点上的变量或者变量的组合是以最小的错分率获得的比较显著的特征［9］。CART的这些特性使其能够快速准确的提取有效特征，解决了样本特征维数高、难以抽取的问题，是一种嵌入到学习算法中的特征选择方法。支持向量机（SVM）是由Vapnik［10］最初在统计学习理论的基础上建立起来的一种机器学习方法。它是近年来发展起来的一种人工智能技术，SVM较好的解决了小样本、非线性、高维数、局部极小点等实际问题，具有很强的泛化能力［11］。最小二乘支持向量机（LSSVM）是标准支持向量机的一种扩展，是支持向量机在二次损失函数下的一种形式［12］，它与支持向量机的主要区别在于采用了等式约束，并将求解优化问题转成求解线性方程，避免了求解耗时的受约束二次规划QP问题，求解速度相对加快。

1　理论与算法

1.1分类回归树

分类回归树（Classification and Regression Tree，CART）采用二分递归法，利用训练样本构造一棵结构简洁的二叉树，是一种有监督的学习算法，将当前训练样本集分为两个子样本集，使得生成的决策树的每个非叶子结点都有两个分支。具体构建分类回归树Tmax的过程如图1所示。

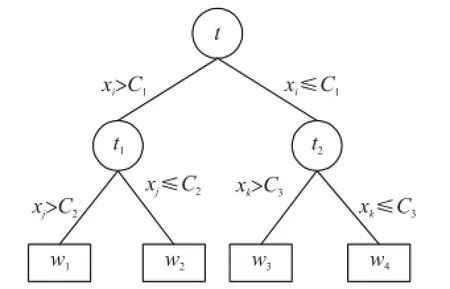
图1　CART树模型简图

所有的数据样本R=｛（Xi，yi）|i=1，2，…，l｝都属于树根节点t，寻找第一个拆分规则S1（即选择整棵树根节点的分支条件）时，首先从变量Xi的第一维x1开始扫描，计算并记录样本数据中该变量的每一个取值作为拆分阈值时节点的不纯度函数下降值Δi（S11，x1），接着扫描变量第二维x2，同样计算并记录该变量的各个不纯度函数下降值Δi（S12，x2），直至扫描完变量最后一维xn，计算并记录所有的拆分阈值对应的不纯度下降值。最后找出不纯度函数下降值最大的拆分规则S1*，满足:

Δi（S1*，xj） =max Δi（S1j，xj） （j=1，2，...，n）（1）

然后找到该拆分规则对应的拆分变量xi和拆分阈值C1，将其定义为树根节点的拆分变量和拆分阈值。此时，已经将整个样本数据集分到两个子树t1和t2上，其中

t1= ｛X∈R : xi≤C1｝ ， t2= ｛X∈R : xi＞C1｝（2）

对于每一个子树，重复以上寻找树根节点拆分规则的扫描过程，寻找每个子树所属子树的根节点的拆分规则。整棵树的建立过程就是一个寻找更小子树根节点的拆分规则的过程。当节点满足以下三种条件之一，即被视作叶节点停止拆分。

①节点很小:分支后的叶节点的样本数小于给定值Nmin（一般取默认值Nmin=10）；

②纯节点:分支后的叶节点中的样本为同一类；

③空属性向量集:无属性向量用作分支选择。

停止拆分后，根据节点ti中来自每个类的样本比例，可以对每个子叶节点wi（i=1，2，…，n）指定类别标签yi，即本文中的料位。此时就完成了分类回归树Tmax的构建。树完全生长过程中会出现过度拟合现象，在得到最大分类回归树的基础上，采用最小代价—复杂性剪枝算法对生成的树进行剪枝。经过剪枝之后，得到最优分类回归树。

最后选择出所有分支节点上的拆分变量，得到模型选择出来的有效特征为Xcart

Xcart= xi（t）⋃xj（t1）⋃…⋃xm（tn）（3）

xi（t）表示在节点t选择出来的第i维变量。

本文的不纯度采用基尼不纯度（Gini Impurity），表示一个随机选中的样本在子集中被分错的可能性。当一个节点中所有样本都是一个类时，基尼不纯度为零。假设i的可能取值为｛1，2，…，m｝，令fi是样本被赋予i的概率，则基尼不纯度可通过如下公式计算:

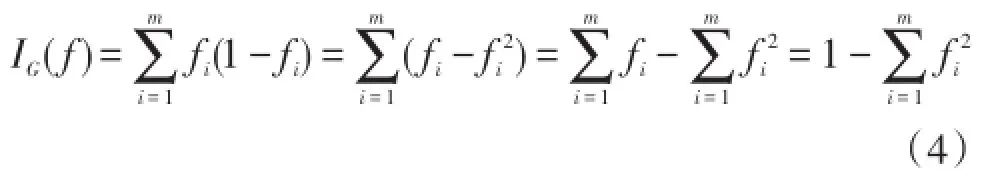
1.2最小二乘支持向量机

SVM是由Vapnik提出的一种用于解决分类与函数逼近问题的机器学习方法，与神经网络的经验风险最小化相比具有更好的泛化能力。LSSVM是在标准SVM上的一种扩展，其需要预先确定的参数也比标准SVM算法少。

设训练样本集为D=｛（xi，yi）|i=1，2，…，l｝，在原始空间中的优化问题可以描述为

约束条件为

yi=wTΦ（xi）+b+ei（6）

式中:xi为输入变量，yi为输出变量，w为权值，b为阈值，γ为正则化参数，ei为误差，优化问题的拉格朗日形式为

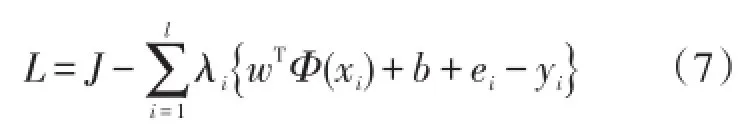
式中:λi为拉格朗日系数，优化问题转化为解线性方程

优化问题的决策函数为

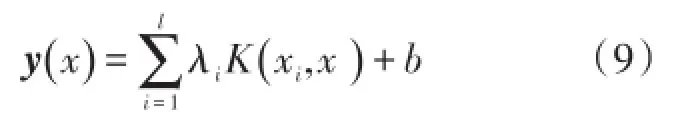
在选定核函数之后，LSSVM需要进一步确定其超参数:正则化参数γ和核参数σ，目前还没有确定γ和σ的统一方法。本文采用耦合模拟退火法（Coupled Simulated Annealing，CSA）与单纯形法（Simplex Method，SM）相结合的方法优化LSSVM的超参数，其主要优化过程分为两步，首先，参数初始化:对于每个超参数，利用耦合模拟退火法（CSA）计算合适的初始值，其搜索范围为［exp（-10），exp （10）］。其次，参数寻优:根据得到的初始值，应用单纯形法进一步对超参数进行优化。

2　建模及实验过程

2.1 基于CART-LSSVM软测量建模

软测量技术主要依据对可测易测过程变量（称为辅助变量）与难以直接检测的待测变量（称为主导变量）的数学关系认识，采用各种计算方法实现待测变量的测量或估计。本文以球磨机轴承振动信号为辅助变量，结合基于分类回归树（CART）的特征选择方法和最小二乘支持向量机（LSSVM）建立球磨机料位的软测量模型。该模型进行软测量的过程主要分为两个阶段，离线建模阶段和在线测量阶段，其流程图如图2所示。

图2　CART-LSSVM系统流程图

具体测量步骤为:①利用振动传感器采集球磨机轴承振动信号。②采用Welch法计算振动信号中时域数据的功率谱并进行频谱的分割，不同频率段的功率谱对应不同的特征［13］，需进一步进行频段的选择，即特征的选择。③根据离线建模阶段得到的CART选择特征变量Xcart，将其做为LSSVM模型输入。④将Xcart输入离线建模阶段所建立的LSSVM模型，预测得出实际料位。

2.2实验过程及数据预处理

采用小型球磨机进行试验数据的采集，振动传感器安装在远离电动机一端的轴承座上，分别采集1 L，2 L，…，20 L共20组振动信号，使用Welch法计算振动信号的功率谱密度（Power Spectrum Density，PSD），将每组PSD均分成22个样本，则样本总数为440个，并把每组的22个样本随机的分成15个训练样本与7个测试样本，因此得到的训练集有300个样本，测试集有140个样本。对PSD进行分析后发现，振动信号的能量主要集中在600 Hz～6 000 Hz之间，因此取这个区间的频谱为有效频谱。综合考虑频谱的波动范围及计算效率，以20 Hz为单位对有效频谱进行分割，并求其均值，所以单个样本的维数是270维。

然后，将训练数据（300×270）输入CART建立分类回归树模型，根据建立的最优树模型，抽取出树的所有分支节点上的拆分变量Xcart，这些变量就是CART选择出的特征对应的维度。本文中，将270维的数据输入CART后，得到最优的回归树模型，其在训练集上的RMSE为0.085 8，选择树模型中的拆分变量得到基本的26维特征，从这270维数据中抽取出这26维，将300×26的训练数据输入LSSVM建立特征变量与料位间的非线性映射。最终，采用与建模数据在同一数据空间的测试数据集（140×270）对CART-LSSVM模型进行测量效果验证。

2.3结果分析与讨论

为了证实本文所建立的球磨机料位测量模型的有效性，在实验的同时采用主成分回归分析（PCR）、主成分分析-最小二乘支持向量机（PCALSSVM）、核主成分分析-最小二乘支持向量机（KPCA-LSSVM）、最小冗余最大相关-最小二乘支持向量机（MRMR-LSSVM）和RELIEFF-最小二乘支持向量机（RELIEFF-LSSVM）5种方法作为对照。采用均方根误差（Root Mean Square Error，RMSE）、平均绝对误差（Average Absolute Error，AAE）和最大绝对误差（Maximal Absolute Error，MAE）作为模型性能评价指标，其中RMSE为主要的评价指标。

式中:yi为第i个样本的真实值，y^i为第i个样本的估计值，N为测试集的样本个数。实验中，LSSVM算法的实现采用J.A.K.Suykens等人开发的LS-SVM-lab1.8Toolbox工具箱。

最小冗余最大相关（Min-Redundancy Max-Relevance，MRMR）是一种经典的基于互信息（Mutual Information，MI）进行特征选择的方法，能选择出单个表示能力较好的特征，并使这些单个较好的特征之间的冗余度最小［14］。RELIEFF是一种启发式的特征选择方法，可以很好的处理有噪音、多标签及有缺失的数据［15］。

表1　不同测试方法测试误差比较

表1给出了几种不同的方法10次预测误差的均值。其中，Ncomp表示降维后所得特征的维数，这里PCR降维后所得预测精度最好的维数为28维，PCA-LSSVM为20维，KPCA-LSSVM为10维。从这几个最好的结果可以看出，PCR和PCA-LSSVM表现普通，分析其原因，主要是由于PCA是一种“线性”降维技术，只能处理线性问题，一方面主成分是原始特征的线性组合，另一方面是由于其对原始数据进行标准化处理，使协方差矩阵变成相关系数矩阵，而相关系数矩阵仅反映指标间的“线性”相关程度。经过KPCA进行非线性降维得到的特征优于PCA得到的特征，对振动信号特征的处理能力较PCA有所提高，但还是不能有效减少特征中的冗余信息，对此类特征的非线性降维难以达到理想的结果。

为了比较MRMR、RELIEFF和CART三种特征选择方法与前三种方法所建立模型的效果，将文中的六种方法均降到26维做对比试验，不同测试方法的最优预测曲线如图3所示，其横坐标表示每个料位下7个测试样本组成的测试样本集，纵坐标表示球磨机的实际料位，单位为升。结合表1可以看出，利用CART得到的特征建模效果较好，该方法有效降低了特征中的冗余信息，自动对特征变量进行选择，并快速将特征降低到较小的维数，为非线性降维的一种有效方法，优于传统的特征选择方法MRMR 和RELIEFF。分析其原因，CART利用基尼系数逐步找出所含信息最大的属性，并递归的建立树模型，能选择出特征中最具区分度的属性作为树的分支，这种机制有效的减少了特征中的冗余信息。从图中可以看出，CART-LSSVM模型的预测精度RMSE= 0.538 5，优于其他对比方法，该方法能较好的跟踪球磨机料位，达到了比较理想的预测精度。

通过对比分析可以发现，CART可以自动将特征变量快速降低到一个较小的维数，避免了特征提取方法的维数选择过程，同时优于传统的特征选择方法，其选择出的特征具有一定的稳定性，可有效的应用于球磨机料位的软测量建模。

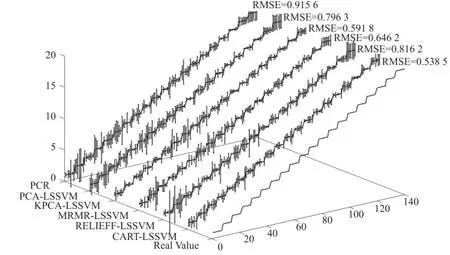
图3　不同方法最优测试结果

3　结论

针对球磨机振动信号中存在较多的冗余特征，本文从选择球磨机轴承振动信号中的有效特征出发，采用分类回归树（CART）建立树模型，选择树干上的频域特征变量，根据得到的特征建立最小二乘支持向量回归模型来进行球磨机料位的软测量。对比试验预测结果表明，该方法具有的优势有:①降维过程中维数的确定不需要人为参与，避免了传统的特征提取及特征选择过程中繁琐的维数调整过程；②具有良好的预测精度，且建模过程简单，易于在实际中操作，算法复杂度不高。

同时该模型有以下待改进的部分，本文中的分类回归树，其拆分规则都只考虑了单个变量，有些情况下需要考虑多变量组合的拆分规则，因此，基于该特征选择方法的软测量建模为需要进一步研究的课题。

［1］ 汤健，柴天佑，丛秋梅，等.基于EMD和选择性集成学习算法的磨机负荷参数软测量［J］.自动化学报，2014，40（9）:1853-1866.

［2］ Tang Jian，Zhao Lijie，Yu Wen，et al.Soft Sensor Modeling of Ball Mill Load via Principal Component Analysis and Support Vector Machines［J］.Lecture Notes in Electrical Engineering，2010（67）: 803-810.

［3］ 付华，王馨蕊，王志军，等.基于PCA和PSO-ELM的煤与瓦斯突出软测量研究［J］.传感技术学报，2014，12:1710-1715.

［4］ 汤健，郑秀萍，赵立杰，等.基于频域特征提取与信息融合的磨机负荷软测量［J］.仪器仪表学报，2010，31（10）:2161-2167.

［5］ Tang Jian，Wang Dianhui，Chai Tianyou.Predicting Mill Load Using Partial Least Squares and Extreme Learning Machines［J］.Soft Computing，2012，16（9）:1585-1594.

［6］ 汤健，柴天佑，赵立杰，等.融合时/频信息的磨矿过程磨机负荷软测量［J］.控制理论与应用，2012，29（5）:564-570.

［7］ Loh W Y.Classification and Regression Trees［J］.Wiley Interdisciplinary Reviews:Data Mining and Knowledge Discovery，2011，1 （1）:14-23.

［8］ Bittencourt H R，Clarke R T.Feature Selection by Using Classification and Regression Trees（CART）［J］.The International Archives of the Photogrammetry，Remote Sensing and Spatial Information Sciences，2004:66-70.

［9］ Gomez-Chova L，Calpe J，Soria E，et al.CART-Based Feature Selection of Hyperspectral Images for Crop Cover Classification［C］// IEEE International Conference on Image Processing，2003，3（2）: 589-592.

［10］Vapnik V N.The Nature of Statistical Learning Theory［J］.Neural Networks IEEE Transactions，1995，10（5）:988-999.

［11］赛吉尔呼，戴盛芳，董爱华，等.基于SVM和RBFN的汽车主动降噪系统传感器故障诊断［J］.传感技术学报，2014，27（4）: 512-517.

［12］Suykens J A K，Vandewalle J.Least Squares Support Vector Machine Classifiers［J］.Neural Processing Letters，1999，9（3）:293-300.

［13］汤健，赵立杰，岳恒，等.湿式球磨机筒体振动信号分析及负荷软测量［J］.东北大学学报:自然科学版，2010，31（11）:1521-1524.

［14］Peng H，Long F，Ding C.Feature Selection Based on Mutual Information Criteria of Max-Dependency，Max-Relevance，and Min-Redundancy［J］.Pattern Analysis&Machine Intelligence IEEE Transactions，2005，27（8）:1226-1238.

［15］Kononenko I，Šimec E，Robnik-Šikonja M.Overcoming the Myopia of Inductive Learning Algorithms with Relieff［J］.Applied Intelligence，1997，7（1）:39-55.

张兴（1990-），男，硕士研究生，研究方向为机器学习，智能信息处理，zhangxing0265@link.tyut.edu.cn；

阎高伟（1970-），男，博士，教授，主要研究方向为智能信息处理和多传感器信息融合，yangaowei@tyut.edu.cn。

Soft Sensor for Ball Mill Fill Level Based on CART-LSSVM Model*

ZHANGXing1，LI Wei1，YAN Gaowei1*，PANG Yusong2
（1.College of Information Engineering，Taiyuan University of Technology，Taiyuan 030024，China；2.College of Mechanical，Maritime and Materials Engineering，Delft University of Technology，Delft，Holland）

Ball mill is a high energy consumption equipment used in electricity，grinding and metallurgical industries.Accurate measurement of its fill level（FL）can improve operational efficiency and safety performance.However，The real-time measurement of FL is difficult to realize，and the components of bearing vibration of ball mill are complex and redundant.Aiming at these problems，a new soft sensor approach of FL based on Classification and Regression Tree（CART）and Least Squares Support Vector Machine（LSSVM）is proposed.Firstly，the Power Spectrum density（PSD）of bearing vibration is obtained by welch method，essential features are achieved by partition subsequently.Secondly，these features are adopted to build CART，and branch nodes of the best model is selected as features.Finally，the LSSVM are used to implement the non-linear mapping between features and FL.The comparative experiments verifies that this model is feasible and practical with high prediction accuracy.

ball mill fill level；soft sensor；feature selection；classification and regression tree；least squares support vector machine；vibration signal

TP29

A

1004-1699（2015）09-1361-06

项目来源:国家自然科学基金项目（61450011）；山西省自然科学基金（2015011052）

2015-05-07修改日期:2015-06-24