生成树的计数
2015-08-17郑艺容
郑艺容,周 雪
(1.厦门理工学院应用数学学院,福建 厦门 361024;2.福州大学离散数学中心,福建 福州 350003 )
生成树的计数
郑艺容1,2,周雪2
(1.厦门理工学院应用数学学院,福建 厦门 361024;2.福州大学离散数学中心,福建 福州 350003 )
从组合数学的角度研究生成树的计数.先利用容斥原理,得到3个组合恒等式,再从组合数学的角度出发,并利用数学归纳法给出了Cayley’s公式的又一简便证明.该计数方法将图的计数问题与组合数学中的经典问题联系起来,更好地揭示了生成树计数的本质.
Cayley’s公式;生成树;容斥原理;数学归纳法
计算图的不同生成树的个数是图的计数问题中的一个重要研究课题.1857年,Cayley[1]在研究给定碳原子数n的饱和碳氢化合物(CnH2n+2)的同分异构体的数目时,提出“树”的概念, 即不含圈的连通图.如果连通图G的一个子图T是一棵树,且包含G的所有顶点,则该子图T称为G的生成树(SpanningTree).设G是一个图,t(G)表示G中不同生成树的个数.Cayley于1889年给出计算n阶完全图的不同生成树个数的公式,即著名的Cayley’s公式.
定理1[2](Cayley’s公式)n阶完全图的不同生成树的个数
Cayley’s公式有很多不同的证明方法,参见文献[2-5].本文又给出Cayley’s公式的又一简单证明.
1 预备知识
首先介绍一些基本概念和结论.容斥原理是组合数学中一个非常重要的定理,其内容如下:
定理2[6 ](容斥原理)设A是有限集,Ai⊆A(i=1,2,…,n,n≥2),则
设N={1,2,…,n},M={1,2,…,m},A表示N上所有p维数组构成的集合, 其中p 定理3设n,m,p∈N+,p 又A=A1∪A2∪…∪Am,根据容斥原理、对称性及引理1可得: 特别地,当p=n-2时可得以下推论: 证明由上述定义可知:T1∩T2∩…∩Tk那么表示顶点1,2,…,k(1≤k≤n)均为树叶的n阶生成树构成的集合,这样的任意一棵树可经过下述两个步骤得到. (i)由顶点k+1,k+2,…,n导出的子图T是一棵树,易知恰好有tn-k个这样的T; 证明T表示所有n阶生成树构成的集合,Ti(i=1,2,…n)表示所有n阶生成树中顶点i为树叶的生成树构成的集合,由于每棵非平凡树至少有两片树叶,故T=T1∪T2∪…∪Tn,由容斥原理、对称性及引理2可知: 以下给出Cayley’s 公式的另一证明. 定理4所有不同n阶生成树的个数tn=nn-2( Cayley’s 公式) 证明用数学归纳法 (i)易知t1=t2=1,t3=3 结论显然成立. (ⅱ)假设定理对小于n的正整数都成立. (ⅲ)以下证明对n结论成立.根据引理3 注3第1,第2,第3个等号成立分别根据 引理3,归纳假设第2步, 推论1. Cayley’s 公式是图计数中的经典公式,已有很多不同的证明方法,本文利用由容斥原理得到的组合恒等式并借助数学归纳法给出Cayley’s 公式的又一简单证明.接下来可进一步研究Cayley’s 公式的不同证明方法,特别是能将图的其它经典问题与图的计数问题联系起来证明Cayley’s 公式,更好地揭示图论中的一些本质联系. [1]CAYLEY A.On the theory of the analytical forms called trees[J].Philophical Magazine,1857,13(4):172-176. [2]CAYLEY A.A theorem on trees[J].Quart J Math,1989,23:376-378. [3]SHOR P W.A new proof of Cayley’s formula for counting labeled trees[J].J Combin Theory:Series A,1995,71:154-158. [4]ARIANNEJAD M,EMAMI M.A new proof of Cayley’s formula for counting labeled spanning trees[J].Electronic Notes in Discr Math,2014,45:99-102. [5]GODSIL C,ROYLE G.Algebraic graph theory[M].New York:Springer-Verlag,2001. [6]曹汝成.组合数学[M].广州:华南理工大学出版社,2000. 2 (1.SchoolofAppliedMathematics,XiamenUniversityofTechnology,Xiamen361024,China;2.CenterforDiscreteMathematics,FuzhouUniversity,Fuzhou350003,China) (责任编辑晓军) Counting Spanning Trees ZHENG Yi-rong1,2, ZHOU Xue Inthispaper,weexploredthepossibilityofcountingspanningtreeinacombinatorialapproach.Wegotthreecombinatorialidentifiesapplyingtheinclusion-exclusionprinciple.Basedontheseidentifiesandmathematicsinduction,wegaveaneasyprooffortheCayley’sformulausingacombinatorialargument.Theapproachcombinestheproblemofgraphicalenumerationwithclassicalproblemsincombinatorialmathematicsandrevealstheessenceoftheproblemofcountingspanningtreeswithbettereffect. Cayley’sformula;spanningtrees;inclusion-exclusion;induction 2014-09-24 2015-02-02 国家自然科学基金项目(NSFC11301440 );福建省教育厅科技项目(JB13155);厦门理工学院科研基金项目(XKJJ201106) 郑艺容 (1979- ),男,讲师,硕士,研究方向为组合图论.E-mail:yrzheng@xmut.edu.cn O157A 1673-4432(2015)01-0095-03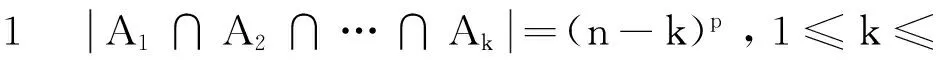

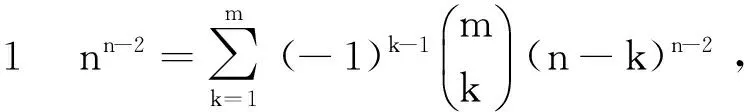
2 生成树计数公式的再证明


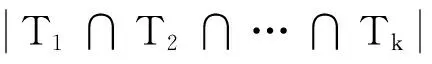
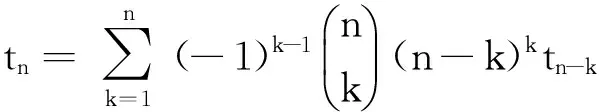
3 小结
