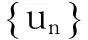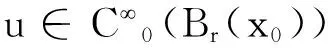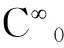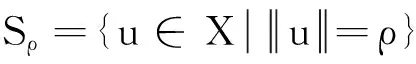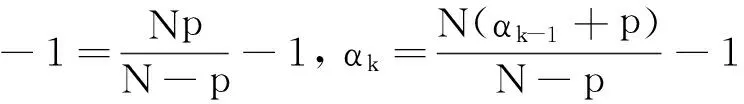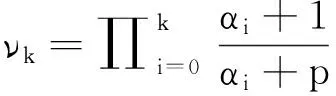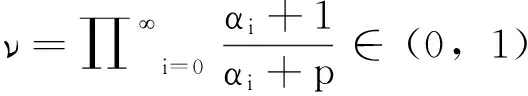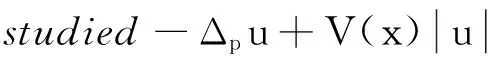一类p-Laplace方程的无穷多解

周　正

(厦门理工学院应用数学学院，福建 厦门 361024)

一类p-Laplace方程的无穷多解

周正

(厦门理工学院应用数学学院，福建 厦门 361024)

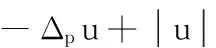
p-Laplace方程；Clark定理；变分方法；无穷多解

Clark定理[1]首先被D.C.Clark提出，它是研究临界点理论的一个重要工具，经常被用于研究带有对称性的次线性微分方程.H.P.Heinz随后给出了另一种形式的Clark定理：

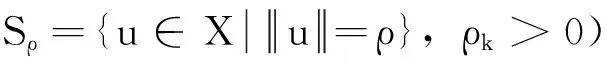
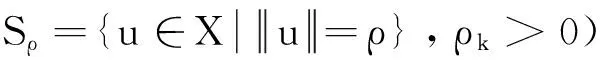
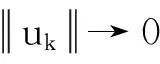
文献[3]利用定理2，考虑了如下p-Laplace方程：

(1)

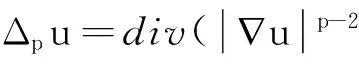
定理3假设方程(1)满足如下条件：

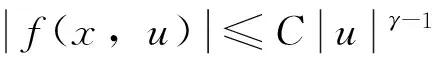
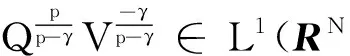
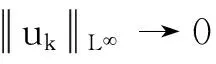
在文献[4-6]中也有类似p(x)-Laplace方程，其(PS)条件往往由类似Ambroseti-Rabinowitz条件保证，而文献[3]中的V满足的条件对紧性有重要影响.注意到：若定理3中的条件(a2)中的M为一常数，比如M=1∉L1(RN)，结论还成立吗？作者因此考虑p>1时一类最特殊情形，即Q(x)=V(x)=1时对应的方程：

(2)

本文通过对f进行某些限制，采用类似文献[3]的方法，我们得到了如下结果：

定理4假设方程(2)满足如下条件：

(*) 存在正数δ>0,1≤γ0使得f∈C(RN×[-δ,δ],R),f关于u为奇函数,且

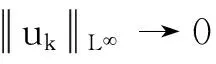
1　证明过程

首先定义方程(2)的解：

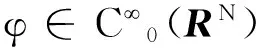
下面分3步来证明定理4.

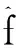
(3)

它是如下泛函对应的Euler方程

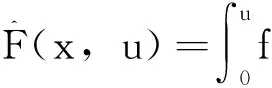
容易证明Φ∈C1(X,R),Φ为偶泛函,且Φ(0)=0.对于u∈X, 利用f的性质，有

注意到1≤γ

(4)

首先证明I2→0.

(5)

即

(6)

(7)

结合Sobolev不等式有

(8)

由(8)迭代得：

(9)

(10)

[1]CLARK D C.A variant of the Lusternik-Schnirelman theory[J].Indiana Univ Math J，1972，22:65-74.

[2]HEINZ H P.Free Lusternik-Schnirelman theory and the bifurcation diagrams of certain singular nonlinear systems[J].J Diff Eqn,66(1987),263-300.

[3]LIU Z,WANG Z Q.On Clark’s theorem and its applications to partially sublinear problems[J].Ann I H Poincar C AN,2014,108:18-213.

[4]ZHIKOV V V.Averaging of functionals of the calculus of variations and elasticity theory[J].Izv Akad Nauk SSSR Ser Mat,1986,50(4):675-710.

[5]ACERBI E,MINGIONE G.Regularity results for stationary electro-rheological fluids[J].Arch Ration Mech Anal,2002,164(3):213-259.

[6]LIU Z,WANG Z Q.Schrödinger equations with concave and convex nonlin-earities[J].Zangew Math Phys,2005,56:609-629.

(责任编辑晓军)

Infinitely Many Solutions to a p-Laplace Equation

ZHOU Zheng

(CollageofAppliedMathematics,XiamenUniversityofTechnology,Ximaen361024,China)

p-Laplaceequation;Clarktheorem;variationalmethod;infinitelymanysolutions

2014-11-02

2015-01-21

福建省教育厅科技项目(JA11240)

周正(1980-)，男，讲师，博士，研究方向为偏微分方程.E-mail:zhouzhengslx@163.com

O175.29

A

1673-4432(2015)01-0091-04