基于最小化界外密度的SVDD参数优化算法
2015-08-17王靖程张彦斌任志文
王靖程,曹 晖,张彦斌,任志文
(1.西安热工研究院有限公司,陕西西安710043;2.西安交通大学电气工程学院,陕西西安710049)
基于最小化界外密度的SVDD参数优化算法
王靖程1,曹 晖2,张彦斌2,任志文1
(1.西安热工研究院有限公司,陕西西安710043;2.西安交通大学电气工程学院,陕西西安710049)
支持向量数据描述(support vector data description,SVDD)是一种具有单类数据描述能力的数据分类算法,因具有结构风险最小化的特性而受到广泛关注。SVDD的参数优化是影响其分类效果的关键问题,本文通过引入样本点的密度信息,提出了以界外密度最小化为目标的参数优化函数,避免了漏检率的计算问题,可充分利用训练数据的分布信息,提高数据描述能力,降低错分率。仿真实验和UCI标准数据库的对比验证表明,优化后的SVDD算法能够有效降低漏检率和错分率,提高算法性能。
支持向量数据描述;参数优化;密度
0 引 言
支持向量数据描述(support vector data description,SVDD)算法是由Tax和Duin于1999年提出的一种单分类算法[1]。SVDD期望获得最小化包含样本数据的超球体,用以区分正常数据和异常数据。由于异常数据采集困难,单分类算法在故障诊断、图像处理、异常检测、医学信号处理等多个领域有大量研究,具有广阔的应用前景[2-4]。
众多学者针对SVDD的性能优化提出了多种思路:文献[5]提出通过核主成分分析(principal component analysis,PCA)将训练数据映射为单位方差的对称球形分布,再训练SVDD模型提升算法性能;文献[6]仿照支持向量机参数优化方法,通过加入或构造异常样本数据,计算最小错分率获取最优参数;文献[7]提出通过最近邻算法增加支持向量数目,从而改善边界形状的算法;文献[8]考虑了样本点的密度信息,提出了一种基于相对密度指数加权的新距离测度,提高算法性能;文献[9]考虑到样本协方差矩阵的信息,提出利用马氏距离替代欧式距离的方法;文献[10]又进一步提出在马氏距离的基础上,加入模糊C均值聚类思想度量样本点距离关系,改进SVDD性能;文献[11]提出采用超椭球体替代超球体,以增强SVDD对不同数据分布的适应能力。上述方法通过对训练数据的处理或距离量度的改进,提高了SVDD的分类准确率,但是对于算法中参数的选取缺少研究,算法性能难以达到最优。
SVDD中一般采用高斯核函数以满足不同数据分布下的边界曲线要求,因此SVDD中有两个调节参数:惩罚参数C与核参数σ,边界曲线的形状同时受到两个参数的影响。Tax等人对参数影响进行了分析,提出通过支持向量的数目近似估计虚警率,并假设惩罚参数C的影响较小,通过迭代方法优化核参数σ,按照支持向量数目百分比接近设定虚警率的目标,得到参数的最优值[1]。进一步研究表明,采用高斯核函数的SVDD算法与单类支持向量机等价,参数C的取值范围可设为C≤(N和ν分别为样本数和虚警率),然后通过迭代方法寻找支持向量数百分比最接近设定虚警率的σ值[12]。由于单分类问题缺乏其他类样本数据,无法利用交叉检验最小化错分率的方法优化参数,Tax又提出了一种基于模型复杂度的优化方法,通过调整参数σ控制模型复杂度的增加,从而避免边界曲线过拟合[13]。鉴于单类支持向量机的虚警率可通过ν值设定,而采用高斯核函数的SVDD又与单类支持向量机等价,因此一些文献采用C=确定参数C。文献[14]提出在设定的虚警率下,用支持向量百分比替代实际虚警率的期望值,寻找支持向量数最小的σ值。文献[15]指出,核函数的作用是将训练数据映射到高维空间,成为超球形分布后再构造包含目标数据的超球体,通过选取合适的核参数将使得高维空间中的数据分布更接近超球形,从而取得更好的分类效果。文献[16]提出利用Bootstrap方法,通过最小化超球体半径与支持向量百分比之和优化核参数。上述方法均基于C=假设,从核参数优化的角度考虑了参数选取问题。但在SVDD算法中,训练数据的虚警率根据支持向量的百分比确定,惩罚参数C与核参数σ都对支持向量数目有着重要影响,固定参数C的取值缩小了参数寻优的范围,无法保证算法性能最优。
文献[17]采用模拟退火算法优化SVDD参数。文献[18]从理论上证明了SVDD受参数影响导致超球体半径的不唯一性,并指出了半径的优化区间。文献[19]详细描述了参数C和σ分别改变时边界形状和支持向量数的变化趋势。文献[20]提出,为了获取参数的最优值,需通过交叉检验搜索不同参数对下的错分率,从而选择出最优参数对。文献[21]研究了SVDD与核密度估计的关系,指出SVDD中无界支持向量是为了保证鲁棒性而拒绝的假设异常样本点,因此应尽量位于低密度区以使边界曲线紧密包围高密度区样本点。
本文首先对SVDD参数调整的影响进行了分析,定义相对密度指数代表样本点聚集程度,提出了以界外密度最小化为目标的参数优化函数,避免了漏检率的计算问题,并通过仿真实验和UCI数据库对比验证了不同参数优化方法的效果。
1 SVDD参数影响分析
由SVDD公式可知,SVDD的边界形状完全由αi>0的支持向量确定,因此本文首先分析参数调节对支持向量及边界形状的影响,然后提出一种新的参数优化方法。
惩罚参数C能够控制支持向量数目,从而影响算法错分率,在不考虑核函数的情况下,当C=时,所有样本点
都成为支持向量,模型严重过拟合,无法接受任何新的数据样本。随着参数C的增加,更多样本被超球体包围,支持向量数目逐渐减少,直至C=,达到设定的样本拒绝率。继续增大参数C,会使得支持向量数目持续减少至构成超球体的最小数目,C=1时,所有训练样本点都在超球体内,模型严重欠拟合。因此C的取值范围是

引入高斯核函数K后,核参数σ能够改变映射到高维空间后的样本点之间的距离,从而影响超球体的半径和原始空间的边界形状。当σ非常小时,K(xi,xj)≈0,所有样本点都成为支持向量。随着参数σ的增加,边界形状变得越来越平坦,支持向量数目逐渐减少。由文献[12]可知,当取C′=2C/σ2时可以近似获得与未加入核函数时相同的SVDD表达式。可以看出,新参数C′同时受到σ的影响,因此加入核参数后,参数C取值范围也会受到σ的影响。
为了直观描述参数对边界形状的影响,本文利用100个二维Banana数据样本对SVDD模型进行训练,参照支持向量机中的参数优化过程,参数C和σ的变化范围分别为2-5~25和20~210,预设的样本拒绝率为10%。图1显示了不同参数组合下SVDD的边界形状,其中同一行的子图像具有相同的C值,而同一列的具有相同的σ值。从图1可以看出,随着σ的增加,边界曲线明显平坦,模型复杂度降低,包围的样本空间范围更大。而随着C值的增加,更多的样本点被包围在了边界曲线内,支持向量的数目明显减少。
4.3.1 选择健薯,提早育苗。选用健康种薯,剔除病、杂、退薯块,确保品种纯度。日平均气温稳定在7~8 ℃开始育苗。在薯苗发芽出土阶段,床土温度控制在32~35 ℃;齐苗后夜催日炼,采苗前5~7 d进行炼苗,苗高20 cm以上时,及时采苗。

图1 不同参数下的SVDD边界形状
图2描述了不同参数组合下支持向量数目的等高线图,支持向量的数目被标在了图中的等高线上。由图可见,对于确定的支持向量数,存在C和σ的最低界限值。因此对于设定的样本拒绝率存在一个调节区间,在该区间内C和σ共同作用影响支持向量的实际数目,超过该区间后,C或σ到达最低界限值,支持向量数受参数极值影响无法达到设定的数目。从图2中还可以看出,在满足预设虚警率的前提下,可通过网格搜索找到多组满足要求的参数对,在仅有单类数据的情况下如何确定寻找最优参数组的目标函数成为优化的关键问题。一些研究中将参数C按照期望的虚警率固定后,只调节参数σ,此种方法缩小了参数的调整范围,只能达到局部最优。
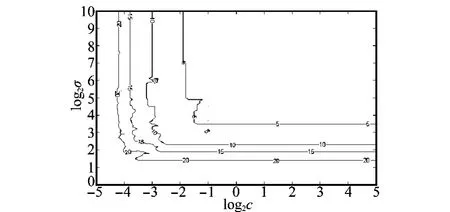
图2 支持向量数的等高线图
图3和图4分别展示了参数C和σ对SVDD模型超球体半径的影响。从图3中可以看出,在确定的σ值下,参数C仅在数值较小时对超球体半径产生影响,达到σ值对应的最小支持向量数后,半径不再发生明显变化,此时σ对超球体半径的控制作用较为明显,参数C的调整几乎无法改变边界形状。当参数C确定时,σ的增加使得超球体半径明显减小,而且超球体半径的大小几乎不因C值变化而改变。由图1结论可知,随着σ的增大边界形状明显趋于平坦,映射到高维空间的数据间距会随之降低,造成超球体半径的减小,但同时原始空间中的边界曲线变得松弛,对目标数据的包围曲线趋向于球形,无法随数据分布的变化而贴切描述,会导致虚警率升高。因此参数优化时应尽量考虑σ值较小的参数组合,从而获得紧凑的边界形状。
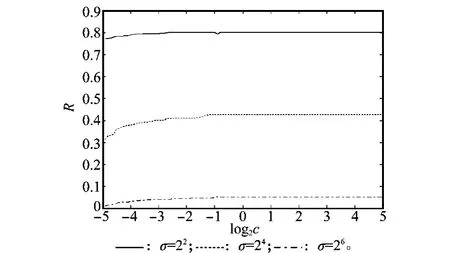
图3 参数C对超球体半径的影响

图4 参数σ对超球体半径的影响
2 SVDD参数优化
综合上述分析,为了在预设的虚警率下选择边界描述紧凑的SVDD参数组,提高SVDD算法性能,需充分利用样本分布信息。本文通过估计样本点分布密度,提出了最小化界外密度的参数优化算法,寻找平均密度最小的无界支持向量,将非支持向量样本点信息纳入寻优过程,使得参数选择中优先考虑将密度较大的样本点包围在超球体内,获得包含大多数高密度样本点的紧凑边界。
本文首先定义相对密度指数,用以代表样本点的聚集程度,由于该指数仅仅用来表示样本点密度的相对大小,因此采取高斯函数获取平滑的密度估计,按如下形式计算:
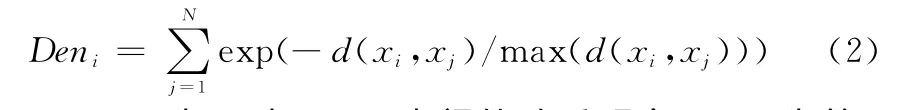
式中,d(xi,xj)为xi与xj两点间的欧氏距离;Deni为第i个样本点的相对密度指数,该指数是点xi与其他所有点的相对密度估计之和。从式(2)可以看出,样本点xi与周围样本点距离越近,Deni数值越高,表示xi所处位置相对其他样本点的密度越高。由于通过支持向量数估计的虚警率并不连续,具有跳跃性,在支持向量数无法满足预设的虚警率时,本文定义了容许值ε=max(1,0.1νN),ν和N分别为预设虚警率和样本数,则优化参数的目标函数为
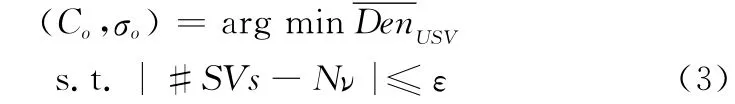
步骤1 采集训练样本,设定样本拒绝率ν;
步骤3 按照网格搜索法,计算当前参数组合下的SVDD模型,并由式估算虚警率;
步骤4 若虚警率满足式(3)中的条件,则进入下一步计算,否则执行步骤6;
步骤5 记录无界支持向量的平均相对密度指数和当前的参数组合,继续下一步;
步骤6 按照设定步长改变参数值,返回步骤3继续运算,若参数搜索完毕,则结束搜索过程;
步骤7 根据所得结果分析步长是否合适,若需调整步长则返回步骤2;
步骤8 在满足式(3)条件的参数组合里,选择平均相对密度指数最小的一组参数组合为最优参数组,若有多对参数组合的平均相对密度指数是相同的最小值,则选取σ最小的一组为最优参数组。
3 仿真实验及结果分析
为了验证参数优化方法的有效性,本文分别利用人工数据集和UCI数据库进行了对比验证。人工数据集采用二维Banana型分布数据,通过不同算法选择最优参数,比较了在同一样本拒绝率下不同优化方法得到的SVDD模型边界形状。UCI数据作为机器学习领域算法测试的标准平台,常被用来比较不同优化算法的虚警率和漏检率,本文选择UCI数据库中的Iris、Wine、Sonar和Breast Cancer Wisconsin数据集进行测试,将一类数据作为目标数据,其他类数据作为异常数据,采用10次独立循环的10折交叉检验算法计算分类效果。本文采用的SVDD参数优化对比算法分别是:利用确定参数C值,再通过搜索σ寻找最接近ν时的σ值,获得最优参数的方法(OS-VDD);利用网格搜索计算参数C和σ不同组合下的计算虚警率,因此3个SVDD模型的支持向量数近似相同,分别为12、10和10,3种方法得到的优化参数组分别为OSVDD(C=0.1,σ=6.498 0)、CSVDD(C=0.287 2,σ=4.287 1)、DSVDD(C=0.176 8,σ=5.278 0)。由图可见,OSVDD方法因参数C值较小,需增大σ值才能使支持向量数接近预设的虚警率,但σ值过大造成边界曲线平坦,形状趋向于球形边界,使得Banana型数据中间凹陷部分也被SVDD边界包围,增大了将其他类数据识别为同类数据的可能性。CSVDD方法明显加强了描述边界的紧凑性,边界曲线随训练样本的分布变化而改变,在中间凹陷部分有效贴近数据,获得了接近香蕉形状的边界曲线,但左侧边界值,将最接近ν时的参数组挑选出来,选择σ最小的参数优化方法(CSVDD);以及本文提出的最小化界外密度方法(DSVDD)。
将OSVDD、CSVDD、DSVDD 3种方法分别应用于具有100个样本的二维Banana型分布数据上,设定ν=0.1,所得边界形状如图5所示。由于3种参数优化方法都按照曲线所包围面积较大。DSVDD方法加入了样本点密度信息,避免了选取中间凹陷部分密度较大的点作为支持向量,使得边界曲线没有过分向中间凹陷,保持了两端边界的适度描述,与其他两种方法相比,DSVDD的边界形状最为贴近香蕉型分布,各部分描述恰当,按DSVDD优化所得的参数组是网格搜索中较为合适的一组。
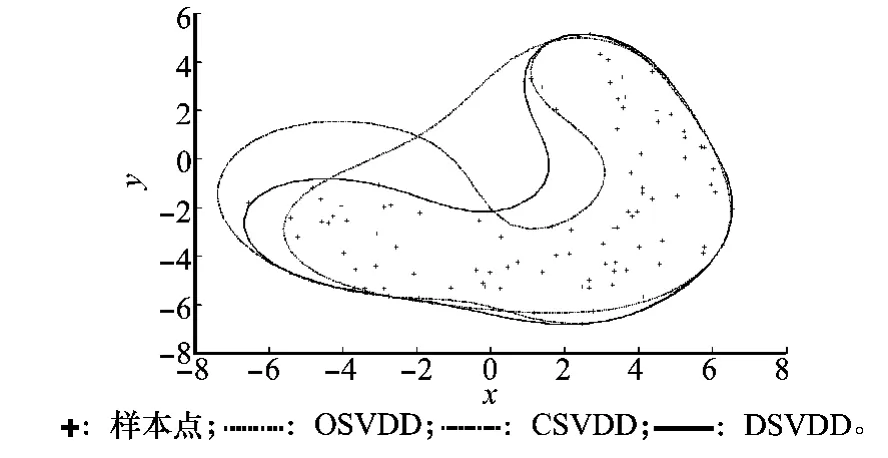
图5 不同参数优化方法对边界形状的影响
为了进一步验证参数优化方法对SVDD模型边界及分类效果的影响,本文选择了4组UCI数据检验3种参数优化方法的错分率(错分样本占总样本数的比例)、虚警率(目标样本被拒绝的比例)及漏检率(非目标样本被接受的比例)。4组UCI数据样本的信息可见表1。
将3种参数优化方法应用于UCI数据,所有训练模型均采用10%的样本拒绝率,将数据中的一类作为目标类,其余作为非目标类,仅用目标类数据训练SVDD所得结果如表2所示。表中结果为10次独立循环结果的平均值,括号内的数据则是10次独立循环结果的标准差,每次独立循环内都要进行10折交叉检验,其均值作为一次独立循环的最终值。
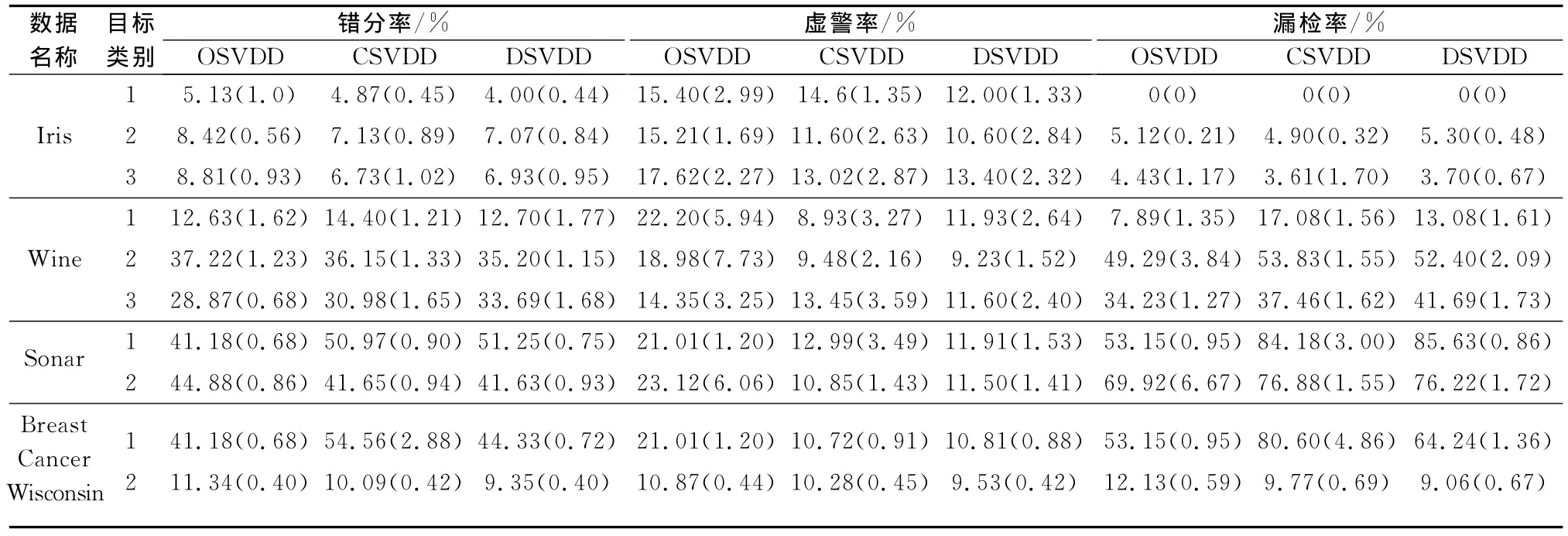
表2 不同优化方法下的UCI数据检验结果
从表2可见,Iris数据中OSVDD的错分率较高,尽管在训练时OSVDD选择了最接近样本拒绝率的σ值,但参数C的固定限制了优化区间,使得另外两种参数优化方法均取得了优于OSVDD的分类效果。从虚警率和漏检率上可以更清楚地发现,OSVDD的C值无法调整使得虚警率较高,从而造成了其较差的分类效果。CSVDD降低了虚警率,DSVDD则更进一步压缩边界包围中样本聚集密度较低的区域,使得模型边界优先包围高密度区域,从而能够更好地发挥SVDD数据描述能力,在保持漏检率基本相同的情况下,DSVDD比CSVDD进一步降低了虚警率。Wine数据中,3种方法的错分率相差较小,但OSVDD的C值固定使得训练时样本拒绝率高于预设值,从而造成虚警率过高和漏检率下降,CSVDD和DSVDD的虚警率都在预设值附近,所以漏检率和错分率反而有所增加。但SVDD训练时需首先保证虚警率满足要求,在此基础上尽量降低漏检率和错分率,因此OSVDD的结果并不是最优的。DSVDD在第1类和第2类目标样本中,都有效降低了漏检率,使得错分率低于CSVDD,但在第3类目标样本中略高于CSVDD,表明此时的优化空间有限,原始空间中其他类样本与目标样本较为贴近,使得边界曲线的调整对漏检率影响较大。Sonar数据中的第1类目标数据和Wine数据情况类似,都是虚警率过高而漏检率较低,使得错分率下降。从第2类目标数据中可以看出,CSVDD和DSVDD的网格搜索扩大了参数优化区间,能够在满足样本拒绝率要求的前提下,尽量降低错分率。但数据维数较高,目标类数据和其他类数据比较贴近,也使得DSVDD的描述效果与CSVDD近似相同。在Breast Cancer Wisconsin的第1类目标数据中,OSVDD由于较高的虚警率而使得错分率较低,CSVDD获得了满足要求的虚警率,但参数组并不合适使得漏检率较高,DSVDD优化调整了参数组,在与CSVDD近似的虚警率时,获得了较低的漏检率,使得分类性能提高。在Breast Cancer Wisconsin的第2类目标数据中,CSVDD和DSVDD均能进一步优化参数组合,调整边界形状,从而获得了比OSVDD更低的漏检率和错分率。
4组数据的仿真结果表明,本文所提的基于最小化界外密度的参数优化算法能够挖掘样本数据信息,在预设虚警率下获得较低的漏检率和错分率,有效提高SVDD分类性能。
4 结 论
本文针对SVDD参数优化问题进行了研究,深入分析SVDD参数变化对模型边界的影响,在此基础上提出相对密度指数代表样本点的聚集程度,按照模型边界曲线尽量包围高密度区样本点的原则,提出最小化界外密度函数进行参数寻优,并通过仿真实验对比不同参数优化方法对SVDD分类结果的影响。结果表明,本文提出的参数优化方法能够有效降低SVDD的漏检率和错分率,提高SVDD模型的可靠性。
[1]Tax D M J,Duin R P W.Support vector domain description[J].Pattern Recognition Letters,1999,20(11/13):1191-1199.
[2]Xie Y X,Chen X G,Yu X M,et al.Fast SVDD-based Outlier detection approach in wireless sensor networks[J].Chinese Journal of Scientific Instrument,2011,32(1):46-51.(谢迎新,陈祥光,余向明,等.基于快速SVDD的无线传感器网络Outlier检测[J].仪器仪表学报,2011,32(1):46-51.)
[3]Shin J H,Lee B,Park K S.Detection of abnormal living patterns for elderly living alone using support vector data description[J].IEEE Trans.on Information Technology in Biomedicine,2011,15(3):438-448.
[4]Xie L,Liu X Q,Zhang J M,et al.Non-Gaussian process monitoring based on NGPP-SVDD[J].Acta Automatic Sinica,2009,35(1):107-112.(谢磊,刘雪芹,张建明,等.基于NGPPSVDD的非高斯过程监控及其应用研究[J].自动化学报,2009,35(1):107-112.)
[5]Tax D M J,Juszczak P.Kernel whitening for one-class classification[J].International Journal of Pattern Recognition and Artificial Intelligence,2003,17(3):333-347.
[6]Tao X M,Liu F R,Zhou T X.A novel approach to intrusion detection based on support vector data description[C]∥Proc.of the Industrial Electronics Society,2004:2016-2021.
[7]Guo S M,Chen L C,Tsai J S H.A boundary method for outlier detection based on support vector domain description[J].Pattern Recognition,2009,42(1):77-83.
[8]Lee K,Kim D W,Lee D,et al.Improving support vector data description using local density degree[J].Pattern Recognition,2005,38(10):1768-1771.
[9]Wei X K,Huang G B,Li Y H.Mahalanobis ellipsoidal learning machine for one class classification[C]∥Proc.of the 6th International Conference on Machine Learning and Cybernetics,2007:3528-3533.
[10]Zhang Y,Xie F D,Huang D,et al.Support vector classifier based on fuzzy c-means and Mahalanobis distance[J].Journal of Intelligent Information Systems,2010,35(2):333-345.
[11]GhasemiGol M,Monsefi R,Yazdi H S.Intrusion detection by new data description method[C]∥Proc.of the UKSim/AMSS First International Conference on Intelligent Systems,2010:1-55.
[12]Tax D M J,Duin R P W.Support vector data description[J].Machine Learning,2004,54(1):45-66.
[13]Tax D M J,Muller K R.A consistency-based model selection for one-class classification[C]∥Proc.of the 17th International Conference on Pattern Recognition,2004:363-366.
[14]Banerjee A,Burlina P,Diehl C.A support vector method for anomaly detection in hyperspectral imagery[J].IEEE Trans.on Geoscience and Remote Sensing,2006,44(8):2282-2291.
[15]Zhao F,Zhang J Y,Liu J.An optimizing kernel algorithm for improving the performance of support vector domain description[J].Acta Automatic Sinica,2008,34(9):1122-1127.(赵峰,张军英,刘敬.一种改善支撑向量域描述性能的核优化算法[J].自动化学报,2008,34(9):1122-1127.)
[16]Brereton R G,Lloyd G R.Support vector machines for classification and regression[J].Analyst,2010,135(2):230-267.
[17]Xing H J,Zhao H X.Feature extraction and parameter selection of SVDD using simulated annealing approach[J].Computer Science,2013,40(1):302-305.(邢红杰,赵浩鑫.基于模拟退火的SVDD特征提取和参数选择[J].计算机科学,2013,40(1):302-305.)
[18]Wang X M,Chung F L,Wang S T.Theoretical analysis for solution of support vector data description[J].Neural Networks,2011,24(4):360-369.
[19]Brereton R G.One-class classifiers[J].Journal of Chemometrics,2011,25(5):225-246.
[20]Wang C K,Ting Y,Liu Y H,et al.A novel approach to generate artificial outliers for support vector data description[C]∥Proc.of the IEEE International Symposium on Industrial Electronics,2009:2168-2173.[21]Chen B,Li B,Feng A,et al.Essential relationship between domain-based one-class classifiers and density estimation[J].Transactions of Nanjing University of Aeronautics &Astronautics,2008,25(4):275-281.
E-mail:wangjingcheng@tpri.com.cn
曹 晖(1978-),男,副教授,博士,主要研究方向为工业智能控制、数据挖掘技术。
E-mail:huicao@mail.xjtu.edu.cn
张彦斌(1952-),男,教授,主要研究方向为工业智能控制、信息融合。
E-mail:ybzhang@mail.xjtu.edu.cn
任志文(1962-),男,教授级高级工程师,主要研究方向为工业自动化。
E-mail:renzhiwen@tpri.com.cn
Parameter optimization algorithm of SVDD based on minimizing the density outside
WANG Jing-cheng1,CAO Hui2,ZHANG Yan-bin2,REN Zhi-wen1
(1.Xi’an Thermal Power Research Institute Limited Liability Company,Xi’an 710043,China;2.School of Electrical Engineering,Xi’an Jiaotong University,Xi’an 710049,China)
Support vector data description(SVDD)is a data classification algorithm of one-class data description,which has the minimum structure risk and attracts much attention recently.The SVDD performance of classification results is determined by the parameter optimization.As the sample point density is defined,a parameter optimization function based on minimizing the density outside is proposed.The proposed algorithm can avoid the calculation of miss detection rate during the optimization,and make full use of sample data distribution information to improve the SVDD performance.Compared with the UCI database,the simulation results confirm that the parameter optimization algorithm can reduce the miss detection rate and miss classification rate effectively.
support vector data description(SVDD);parameter optimization;density
TP 391
A
10.3969/j.issn.1001-506X.2015.06.33
王靖程(1982-),男,工程师,博士,主要研究方向为模式识别。
1001-506X(2015)06-1446-06
2014-06-13;
2014-10-22;网络优先出版日期:2014-11-20。
网络优先出版地址:http://www.cnki.net/kcms/detail/11.2422.TN.20141120.1831.005.html
国家自然科学基金(61375055);新世纪优秀人才支持计划(NCET-12-0447);陕西省自然科学基金(2014JQ8365);华能集团科技项目(HNKJ13-H20-04)资助课题
