盾构隧道等效弯曲刚度的简化计算

黄艳香,张孟喜,李 磊

(上海大学土木工程系,上海 200072)

盾构隧道等效弯曲刚度的简化计算

黄艳香,张孟喜,李 磊

(上海大学土木工程系,上海 200072)

在传统刚度有效率研究的基础上,采用弹性力学的变刚度梁计算方法进行了隧道位移和变形的计算,由此得到了简化的纵向刚度有效率计算表达式.实例分析表明：随着螺栓个数的增加和半径的增大,隧道纵向刚度有效率和纵向等效刚度均增大;但是随着螺栓个数的增加,纵向刚度有效率表现为同方向、近线性关系;同时随着螺栓半径的增大,纵向刚度有效率表现为同方向、近抛物线关系;而随着管片厚度和管片混凝土模量的增大,纵向刚度有效率降低.在此基础上考虑由管片刚度改变引起的应力集中,研究了埋深对刚度有效率的影响,结果表明,随着埋深的增加刚度有效率呈线性降低,即隧道纵向等效抗弯刚度减小.研究结果对盾构隧道设计具有一定的指导意义.

刚度有效率;变刚度;应力集中;等效弯曲刚度

近年来,我国的经济发展迅速且人口持续增长,对于城市交通设施建设的需求不断增加,合理利用城市地上和地下空间成为解决这一需求和促进环境保护的最佳选择.目前,许多城市进行了地铁建设,盾构法也逐渐成为地铁隧道施工中一种最常用的方法,使得地铁轨道交通迅速成为我国减小交通压力的主要手段.同时,由于盾构隧道是由管片体通过管片间相互连接而成的,并非一个整体,故在施工和使用的过程中产生许多问题,其中纵向性能的分析是研究的主要方面之一[1].因此,研究盾构隧道的纵向力学性能及其行为分析具有重要意义[2].

在研究的初始阶段,许多学者都认为隧道连接处的刚度越大越好,可是在实践中发现,刚性连接会引发诸如连接处刚度过大导致管片刚度突变处易开裂等问题,因此研究转向了柔性接头.目前来说,修正惯用法是常用的计算方法之一[3],认为隧道接头部分弯曲刚度的降低等同于环整体刚度的降低,并考虑管片多接缝造成的管片刚度降低和管片接头拼装的影响,引进刚度有效率和管片弯矩传递系数进行设计计算.但是由于实际情况的差异,刚度有效率的取值一直是比较盲目的.在试验方面,黄宏伟等[4]基于二环盾构隧道相似结构模型加载试验,发现隧道加载时变形和荷载存在明显的线弹性关系,且隧道刚度有效率为常数,符合修正惯用设计法的理论基础.在理论方面,Lee等[5]采用弹性铰模型,得到了隧道由圆形变为椭圆形之后的水平和竖向刚度之比,由此得到横向等效刚度,并在此基础上给出了隧道横向抗弯刚度的有效率取值范围为0.1～0.6的结论.钟小春等[6]采用梁弹簧模型和修正法分别计算了衬砌环的最大水平位移,并以其作为判断准则,得到刚度有效率的数值,同时算出刚度有效率的取值范围为0.4～0.8.文献[4]对隧道通常采用的接头形式、构造及适应性进行归类,进而对不同接头形式的力学性能进行了分析,得到了不同接头形式对隧道刚度的影响.但目前的研究还较少涉及由通错缝拼装引起的刚度有效率的不同,定量表示也较少[6-7].

目前,已有很多针对盾构隧道刚度有效率的影响因素的研究,一般认为主要因素有：管片种类、尺寸、形状、管片接头的结构特性、管片环相互之间的接头方式及其结构特性、荷载等[8-10].本研究采用弹性理论,通过变刚度梁的变形计算,进行了盾构隧道纵向位移和变形的计算,从而得到简化的纵向刚度有效率的数值计算方法.并且主要考虑环缝连接处螺栓数量、螺栓半径、管片环厚度和混凝土模量对纵向刚度有效率的影响.

1 计算模型

1.1 盾构隧道计算模型

在实际工程中,由于通缝拼装施工简便,且拼装紧密,因此以通缝隧道居多.本研究主要对通缝盾构隧道进行刚度有效率的计算.目前,常用的盾构隧道受力分析方法有荷载结构模型法和地层结构模型法,其中荷载结构法是计算隧道衬砌在荷载作用下产生的内力和变形,计算较为简单,工作量较小;底层结构法是将衬砌与地层看作连续的整体来进行受力分析,计算较为复杂和繁琐.本研究运用荷载结构法,将围岩力简化为均布荷载,即将实际存在较多接缝的隧道等效为均质隧道(见图1),并在此基础上进行了隧道的变形和内力分析.

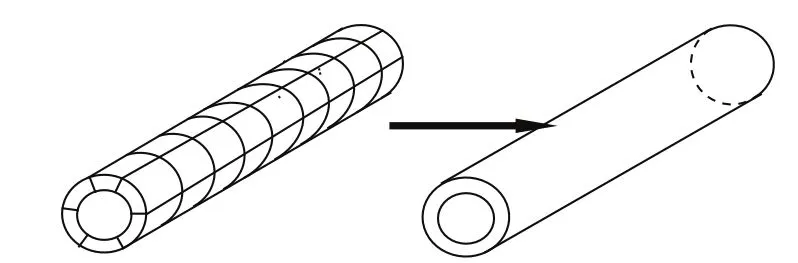
图1 盾构隧道纵向简化模型Fig.1 Longitudinal simpli fi ed model of shield tunnel

根据以上分析,建立如图2所示的计算模型,取由n个管片连接而成的一段隧道,简化成均匀的变刚度梁,两端铰支,即约束隧道两端水平和竖向位移,环缝处用螺栓连接.

图2 盾构隧道受力分析Fig.2 Stress analysis of shield tunnel

1.2 盾构隧道刚度有效率的计算

盾构隧道纵向刚度有效率的一般概念如下：在进行分析计算的过程中,首先将实际存在较多接缝的隧道等效为均质隧道,之后考虑接缝的存在对均质隧道整体刚度的影响,需要将管片刚度折减,刚度有效率为η,(EI)eq=ηEI,其中EI为均匀混凝土管片的刚度.在相同荷载作用下,当实际隧道和等效后均质隧道的转角相等时,则认为二者的刚度相同,此时即可得到隧道刚度有效率η.

计算中采用的基本假定如下.

(1)连接螺栓会对管片产生明显的铰接作用,因此在本计算模型中采用管片环两端简支,将上部土压力简化为均布荷载(见图2).

(2)考虑纵向环缝的影响范围,将管片环纵向依据刚度不同分为三部分：接头处影响宽度为lb(即图2中的阴影宽度),接头作用范围外管片的作用长度为l-2lb.

(3)环缝影响范围内外的隧道截面形状均为圆环.

(4)接头刚度和混凝土管片刚度分别用D1和D0来表示.D1=E1I为接头处混凝土与螺栓的等效刚度,其中E1为环缝处的等效模量;D0=E0I,其中E0为管片混凝土模量.

(5)通过材料力学分析计算环缝处接头刚度,可由变形协调、力平衡条件及弯矩平衡条件得到.简单计算过程如下：随着弯矩的增大,隧道横截面中性轴上移、管片挠曲、接头端面分离,并开始形成局部受压区和局部受拉张开区.受拉张开区衬垫不再承受外荷载,螺栓出露并和受压区衬垫共同作用以抵抗外加荷载.计算过程中由于轴力和剪力作用较小,故忽略轴力和剪力.图3为管片环纵向受弯变形受力分析,其中θ为纵向环缝影响范围内管片环的转角.图4为环缝接头处的受力及变形协调分析,由此计算求解θ,图中a,b分别为管片环横截面的半长轴与半短轴,φ为中性轴位置,ds为管片环上任意微分单元,dα为ds的对应圆心角,x(或x′)为ds与中性轴的距离,δj为环缝影响范围内的最大变形量,Eb为螺栓弹性模量,E0为混凝土的弹性模量,t为管片厚度[11-12].

图3 管片受力分析Fig.3 Stress analysis of segments

图4 环缝接头处的应力应变分析Fig.4 Stress and strain analysis of segments joints

经过计算可得

式中,

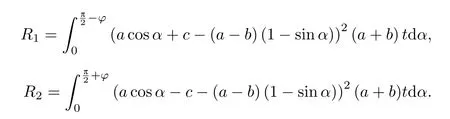
盾构隧道纵向刚度有效率是对隧道本身性质的反映,可以取其中一个环缝连接处进行分析.分析计算时,在外荷载作用下,梁产生弯曲变形,由以上分析可知,取出部分只考虑弯矩作用,单节管片纵向受力分析如图5所示.

由材料力学分析可知,小变形梁挠度曲线的常用计算式为

式中,x为梁上任一点位置,y(x)为梁上任一点的挠度,M(x)为任一点的弯矩,D(x)为变刚度梁任一点处的刚度.

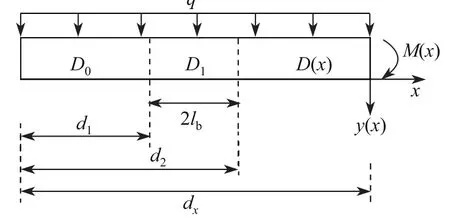
图5 单节管片纵向受力分析Fig.5 Stress analysis of a single segment

刚度的计算利用H(x)函数[13](即Heaviside函数,当x≥0时,H(x)=1;否则H(x)=0),即任意非均质材料变刚度梁的抗弯刚度D(x)=E(x)I(x)均可表示成阶梯刚度.若将梁划分为n+1段,则任意截面的刚度倒数为

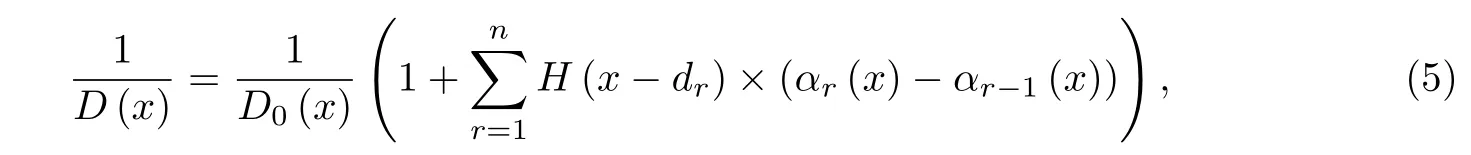
式中,Dr(x)为第r段导数连续的刚度函数,αr(x)=D0(x)/Dr(x)为初始刚度与第r段刚度之比.将式(5)代入(4)中可得

由此可得任意变刚度梁变形积分形式的通式为

式中,y0为梁边界初始位移,θ0为梁边界初始转角,yq(x)为均布荷载作用下产生的位移.

由以上分析可知,梁上任一点的弯矩为

将式(8)代入(7)中可得

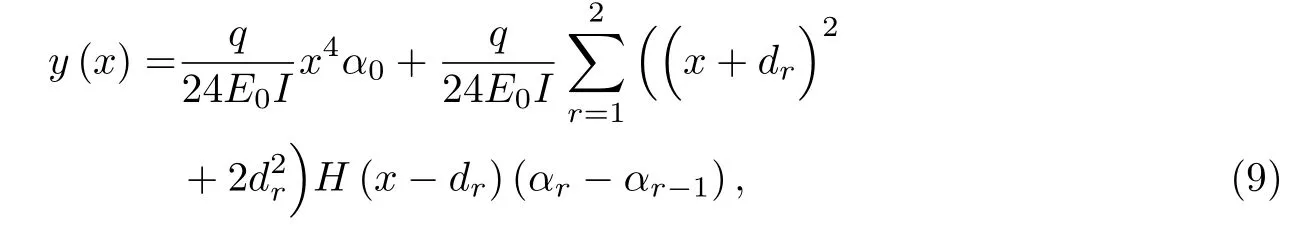
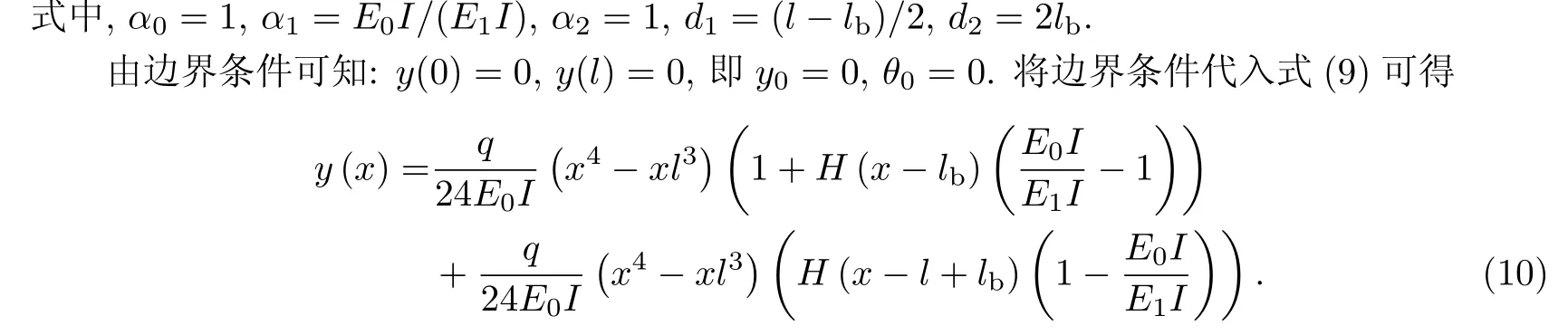
由此可计算出在土压力近似为均布荷载的条件下,管片的转角为

而相同条件下混凝土管片的转角为

由以上结果可以计算得到刚度有效率的表达式为

即利用刚度比值来表示刚度有效率η.将式(3)代入(13)中可得

即纵向刚度有效率的拟合计算公式.

2 实例分析

接头抗弯刚度反映的是管片接头抵抗外荷载作用下的变形能力,与接缝材料特性和管片结构尺寸密切相关.现假定隧道管片设计及材料参数如表1所示,通过第1节推导的理论计算方法进行分析计算,可求得不同变量下的隧道纵向刚度有效率和纵向等效刚度.

表1 管片设计及材料参数Table 1 Design and material parameters of segments

2.1 螺栓个数和半径对η的影响分析

隧道结构的管片环管片厚度为0.35 m,不考虑螺栓预紧力.下面将在隧道结构基本特征的基础上进行影响因素分析,只考虑变化单个因素.

在实际工程中,通缝隧道管片环一般由6个管片组成,1个是封顶块,另外5个是标准块,其中每个标准块纵向用3个螺栓连接,封顶块用1个螺栓连接,则纵向环之间的连接螺栓个数一般为16个.在此分别取螺栓个数为10,15,20,25,研究在不同螺栓个数情况下,纵向刚度有效率和纵向等效刚度的变化规律(见表2和图6).

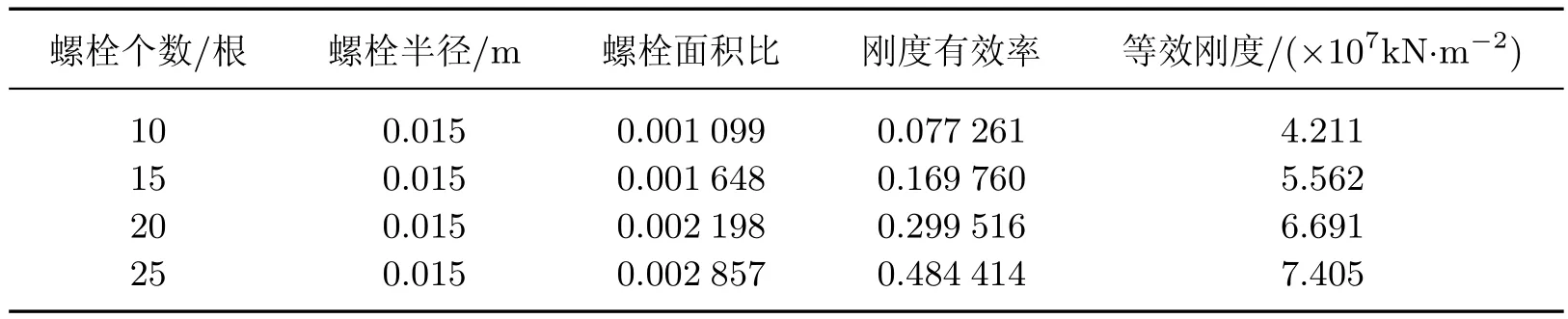
表2 不同螺栓个数条件下的纵向刚度有效率Table 2 Longitudinal rigidity ratios under di ff erent amounts of bolts

由于影响盾构隧道刚度有效率和纵向等效刚度的因素有材料尺寸和材料性质等,故除了连接件螺栓的个数,螺栓半径也会影响η的大小.在实际工程中,常用的螺栓半径有0.014和0.016 m,因此选用表2中半径为0.015 m的螺栓进行计算.表3为当螺栓个数为16,半径分别为0.010,0.015,0.020,0.025,0.030 m时的隧道纵向刚度有效率和纵向等效刚度.纵向刚度有效率的规律如图6和7所示.

图6 不同螺栓数量条件下的纵向刚度有效率Fig.6 Longitudinal rigidity ratios under di ff erent amounts of bolts

表3 不同螺栓半径条件下的纵向刚度有效率Table 3 Longitudinal rigidity ratios under di ff erent bolts radius

图7 不同螺栓半径条件下的纵向刚度有效率Fig.7 Longitudinal rigidity ratios under di ff erent bolts radius

从图6可以看出,刚度有效率与螺栓个数呈线性关系,增幅为0.023 1,可见增加螺栓个数是提高隧道纵向刚度有效率的有效方法,也能有效降低环缝张开量.

图7为不同螺栓半径条件下螺栓面积与隧道刚度有效率的关系.由图7和表3可以看出,螺栓半径的改变会引起螺栓面积比以幂函数增长,而螺栓个数与螺栓面积比则是线性关系,因此螺栓半径的改变对于隧道纵向刚度有效率的影响较大.由此可知,不管是增加螺栓个数还是增大螺栓半径,都相当于增大了接缝的刚度,能有效减小接缝的张开量.盾构隧道中纵向接缝的变形是隧道纵向的主要变形,因此增大任一项都可以增大隧道的纵向刚度.

2.2 管片厚度和模量对η的影响分析

通过以上分析可知,螺栓个数和半径对于盾构隧道纵向刚度有效率的影响比较明显.同时,管片尺寸和材料性质对于盾构隧道纵向刚度有效率的影响相对较小.由分析结果可知,盾构隧道纵向刚度有效率随管片厚度的增加而减小,厚度每增加0.05 m,隧道纵向刚度有效率减小2%左右,比螺栓个数和半径的影响要小(见图8).由此可见,从受力分析角度来看,管片厚度可以适当减薄,但是从实际安全考虑,管片又不宜过薄,因此现有的管片选择是比较合理的.已有研究也表明,与其他东亚国家相比,我国的管片厚度相对较薄;而与西欧国家相比,我国的管片厚度偏厚[14].

图8 纵向刚度有效率随管片厚度的变化Fig.8 Longitudinal rigidity ratios under di ff erent segment thickness

管片混凝土弹性模量对纵向刚度有效率的影响最小,纵向刚度有效率随管片弹性模量的增大而减小,且每增加一个强度等级,纵向刚度有效率降低约0.2%(见图9).虽然刚度有效率降低了,但是由于混凝土强度的增强,所以纵向等效刚度增大,而且增加幅度与混凝土强度成正比,增加比例约与刚度有效率降低的比例相近(见图10),但相对来说影响较小.但是,随着管片弹性模量的增大,隧道纵向等效刚度增大,且几乎是线性增长.可以看到,当混凝土的弹性模量为3.45×104MPa时,有一个微小的反弯点,因此在该点上下的弹性模量最合适,过大或过小都会使增加比例下降.

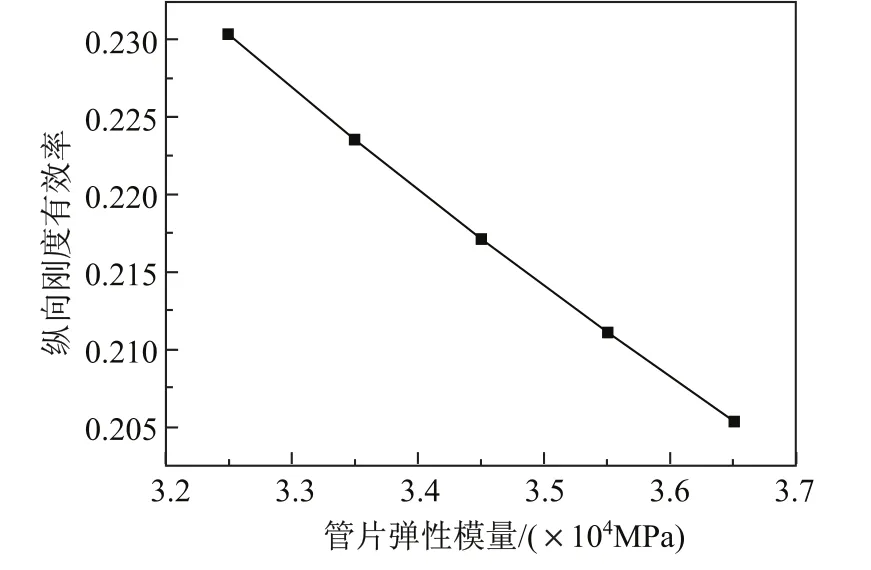
图9 纵向刚度有效率随管片弹性模量的变化Fig.9 Longitudinal rigidity ratios under di ff erent segment modulus of elasticity

2.3 其他因素的影响分析

E1I为环缝接头影响范围内的等效刚度,所以在接头影响范围内外的接触处会有刚度的突变,由应力集中的产生原因可知,在接头影响范围外的管片内会产生应力集中的现象.由变形协调条件可知,应力集中系数与管片刚度和隧道等效刚度的比值相关.经计算得到应力集中系数为α=E1I/(E0I),此时管片的最大应力为σmax=αM/WZ,其中WZ为隧道横截面的弯曲截面系数.由管片的失效情况可知,埋深和环缝处的连接都会影响刚度有效率.等效刚度有效率的计算表达式为η=σmax×WZ/(2M).可知,隧道纵向刚度有效率与埋深成反比,即随着埋深的增加,弯矩增大.在相同连接件情况下,刚度有效率降低,则等效弯曲刚度减小.

2.4 与现有理论的比较

本研究假定管片环为均质环,不考虑环间螺栓的轴向作用和剪切作用,建立了理论计算结构模型;考虑结构的对称性,施加了对称的均布荷载约束,用第1节中的推导公式计算了隧道纵向弯曲刚度与管片环接缝相关的影响因素,其中螺栓个数和半径对η的影响较大,而管片的厚度和管片材料性质对η的影响较小.并且得到如下结论：随着纵向螺栓个数的增加,纵向弯曲刚度呈线性增长,这与钟小春等[6]的结论相似.

本研究得到通缝拼装隧道横向刚度有效率η与各隧道参数的关系如下：接头刚度比增大, η增大;接头数增加,η减小.这个结论与Lee等[5]的研究结果相同.

叶飞等[11]在考虑横向性能的基础上,进行了盾构隧道的纵向等效刚度分析,直接应用考虑横向刚度有效率的修正惯用计算模型——η-ξ法,即管片环横向抗弯刚度的有效性是通过引入横向弯曲刚度有效率来实现的,而横向刚度有效率的取值与变形后隧道的水平直径和竖直直径的变化关系密切,其表达式为η=1/(1+ΔD1/D),其中D为隧道直径,ΔD1为变形后隧道直径的改变量.在进行理论分析之后,采用螺栓个数为16、螺栓半径为0.015 m的模型进行实例分析.在文献[11]中,当横向刚度有效率为0.7时,得到的纵向抗弯刚度理论值为6.614 kN/m2,数值模拟值为6.410 kN/m2,与本研究计算出的纵向刚度有效率理论值极其相似.

本研究还进行了荷载的分析,发现隧道加载时变形与荷载存在明显的线弹性关系,验证了隧道刚度有效率为常数,符合修正管用设计法的理论基础,与黄宏伟等[4]进行的二环均质、通缝拼装、错缝拼装盾构隧道相似结构模型的受压荷载试验所得到的结论类似.

图10 纵向等效刚度随管片弹性模量的变化Fig.10 Longitudinal equivalent rigidity under di ff erent segment modulus of elasticity

3 结论

(1)通过变刚度梁的变形计算进行了纵向刚度有效率的简化推导,并得出纵向刚度有效率和接头刚度及管片环刚度的相关表达式.计算得出的刚度有效率与传统的理论计算值相吻合,并与试验结果相近.

(2)与目前常用的纵向刚度有效率表达式相比,本研究得到的表达式更加简捷,并且考虑了影响纵向刚度有效率的主要因素,忽略了次要因素,可作为设计中的初步依据.

(3)实例分析表明,随着螺栓个数的增加和半径的增大,隧道纵向刚度有效率和纵向等效刚度均增大.但随着螺栓个数的增加,纵向刚度有效率表现为同方向、近线性关系;而随着螺栓半径的增大,纵向刚度有效率表现为同方向、近抛物线关系.所以,在设计施工过程中,若需要增大刚度,可优先选择增大螺栓半径的方法,以提高效率.

(4)分析了管片环厚度和弹性模量对盾构隧道纵向刚度有效率的影响,可以看出管片环厚度和弹性模量的增大都会导致刚度有效率的降低,但是随着管片环模量的增大,纵向等效刚度会增大.

(5)分析了由于刚度突变引起的应力集中对刚度有效率的影响,即在相同连接螺栓的情况下,随着埋深的增加,应力集中的影响越大,刚度有效率减小.因此,在设计埋深较大的隧道时,可以采用刚度较大的连接件.

由于在计算纵向刚度有效率时,主要考虑刚度突变的因素,对于其他因素的分析较少,所以本研究中的拟合条件并不多,只能为设计施工提供一个简要的指导依据,具体还要根据现场实际情况进行分析.

[1]黄茂松,张治国,王卫东,等.软土盾构隧道施工的环境土工效应[J].湖南大学学报：自然科学版, 2008,35(11)：81-87.

[2]CHEHADE F H,SHAHROUR I.Numerical analysis of the interaction between twin-tunnels：in fl uence of the relative position and construction procedure[J].Tunneling and Underground Space Technology,2008,23(2)：210-214.

[3]田敬学,张庆贺.盾构法隧道的纵向刚度计算方法[J].中国市政工程,2001(3)：35-37.

[4]黄宏伟,徐凌,严佳梁,等.盾构隧道横向刚度有效率研究[J].岩土工程学报,2006,28(1)：11-18.

[5]LEE K M,GE X W.The equivalence of a jointed shield-driven tunnel lining to a continuous ring structure[J].Journal of Canadian Geotechnical Engineering,2001,38(3)：461-483.

[6]钟小春,张金荣,秦建设,等.盾构隧道纵向等效弯曲刚度的简化计算模型及影响因素分析[J].岩土力学,2011,32(1)：132-136.

[7]郑永来,韩文星,童琪华,等.软土地铁隧道纵向不均匀沉降导致的管片接头环缝开裂研究[J].岩石力学与工程学报,2005,24(24)：4552-4558.

[8]韦凯,宫全美,周顺华,等.隧道长期不均匀沉降预测的蚁群算法[J].同济大学学报：自然科学版, 2009,37(8)：993-998.

[9]KOYAMA Y.Present status and technology of shield tunneling method in Japan[J].Tunneling and Underground Space Technology,2003,18(2)：145-149.

[10]张治国,黄茂松,王卫东.层状地基中隧道开挖对临近既有隧道的影响分析[J].岩土工程学报,2009, 31(4)：600-608.

[11]叶飞,何川,朱合华,等.考虑横向性能的盾构隧道纵向等效刚度分析[J].岩土工程学报,2011, 33(12)：1870-1876.

[12]张文杰,徐旭,张孟喜,等.广义的盾构隧道纵向等效连续化模型研究[J].岩石力学与工程学报, 2009,28(S2)：3938-3944.

[13]朱先奎.任意变刚度梁变形的通用方程[J].力学与实践,1993,15(3)：58-60.

[14]严佳梁.盾构隧道管片接头性态研究[D].上海：同济大学,2006.

本文彩色版可登陆本刊网站查询：http：//www.journal.shu.edu.cn

Simpli fi ed calculation of shield tunnel’s equivalent bending rigidity

HUANG Yan-xiang,ZHANG Meng-xi,LI Lei
(Department of Civil Engineering,Shanghai University,Shanghai 200072,China)

Based on the studies of conventional longitudinal equivalent rigidity ratio, the tunnel’s displacement and deformation are calculated using a variable rigidity beam elasticity calculation method.A simpli fi ed expression of the tunnel’s longitudinal equivalent rigidity ratio is obtained.The analysis shows that the longitudinal equivalent rigidity ratio is linearly proportional to the number of bolts.At the same time,the longitudinal equivalent rigidity ratio nearly parabolically increases with the increasing of the bolt radius. However,with the increase of segment ring thickness and the segment modulus of elasticity, the longitudinal equivalent rigidity ratio is reducing.Because of the stress concentration caused by the tunnel’s rigidity change,the tunnel longitudinal equivalent bending rigidity and e ff ectiveness of the rigidity reduce with the increasing of depth.The proposed model is more widely applicable and is of reference value for longitudinal stability design of shield tunnels.

rigidity ratio;rigidity mutation;stress concentration;equivalent bending rigidity

U 451

A

1007-2861(2015)01-0106-11

10.3969/j.issn.1007-2861.2014.01.036

2013-12-18

国家自然科学基金资助项目(41172238)

张孟喜(1963—),男,教授,博士生导师,博士,研究方向为新型土工加筋技术及环境岩土工程. E-mail：mxzhang@shu.edu.cn