砖墙基础托换的钢梁-砖砌体Timoshenko组合梁模型分析

项潇潇,吴郦威,杨 骁

(上海大学土木工程系,上海 200072)

砖墙基础托换的钢梁-砖砌体Timoshenko组合梁模型分析

项潇潇,吴郦威,杨 骁

(上海大学土木工程系,上海 200072)

将钢夹梁和钢梁间的砖砌体等效为组合梁,基于Timoshenko弹性梁理论,建立了钢梁-砖砌体组合梁弯曲变形的控制方程,给出了钢梁-砖砌体组合梁弯曲变形的解析解.在此基础上,考虑砖砌体墙的拱效应,研究了砖砌体墙的基础托换问题,得到了不同型号工字钢夹梁的钢梁-砖砌体组合梁最大挠度和最大应力,以及基础单段托换的最大长度.研究结果表明：钢梁-砖砌体组合梁挠度和应力随着工字钢型号编号的增加而减小,但钢梁承担的荷载以及锚栓承担的压力不变.同时,Timoshenko模型的组合梁挠度大于Euler模型的组合梁挠度,但两种模型的应力及紧箍压力相同.因此,Euler组合梁模型可用于基础托换设计中的强度分析,而刚度分析建议采用Timoshenko组合梁模型.

砖砌体;基础托换;组合梁;拱效应;托换长度

我国现存的早期砌体结构大部分已进入修复加固期,并且宫殿、寺庙等古砌体结构亦急需进行加固与修复.因此,砌体结构的加固修复理论和技术研究具有现实意义,且已成为当今结构工程领域广受关注的问题[1].目前,相比于砖柱加固和梁加固的理论研究及工程实践[2-6],针对钢梁砖砌体组合体系[7-8]的研究还相对滞后.在托梁拆墙或基础托换方面,童敏等[9]和赵考重等[10]分别利用钢梁-砌体组合梁和钢梁-混凝土组合梁对某办公楼进行了拆墙改造和拆墙托换,实践发现钢-砌体/混凝土组合梁托换法具有减轻结构自重、增加空间净高等优点.同时,敬登虎等[11]试验研究了钢板-砖砌体组合梁的静力性能,探究了钢板厚度、灌注材料等对截面应变分布和承载力的影响;并将钢板-砖砌体组合梁成功应用于某砖混建筑的拆墙托换中,现场试验验证了拆墙托换方案的可行性和可靠性[12].然而,尚未见到有关钢梁-砌体组合梁较为精确的理论分析报道.

本研究基于某历史保护砖砌体建筑外墙的基础托换问题,利用Timoshenko弹性组合梁理论,建立了钢梁-砖砌体组合梁弯曲变形的控制方程;考虑砖砌体墙的拱效应,分析了砖墙基础单段托换时,不同型号工字钢夹梁的钢梁-砖砌体组合梁最大挠度和最大应力,给出了基础单段托换的最大长度,得到了Timoshenko组合梁和Euler组合梁的结果差异,为砖砌体墙基础托换设计及工法提供理论指导.

1 基于Timoshenko梁理论的钢梁-砖砌体组合梁弯曲变形

图1为基础托换设计中的砖砌体墙,砖墙和钢梁通过沿长度方向均匀分布的钢螺栓连接,且砖墙和钢梁之间垫以木块以达到紧密连接,使钢梁、木块和砖砌体共同作用.记钢梁-砖砌体墙之间的单位长度紧箍压力为N.考虑到木材弹性模量较低,忽略木块的影响,将钢梁和钢梁间的砖墙等效为Timoshenko组合梁,而上部砖墙的重量等效为荷载q,建立如图2所示的两端固支钢梁-砖砌体组合梁力学模型.

设钢梁-砖砌体组合梁长为L,砌体砖的厚和高分别为bc和h,横截面面积与形心主惯轴的惯性矩分别为Ac和Ic,而钢梁翼缘宽和高分别为bs1和hs1,腹板厚为bs2,横截面面积与形心主惯轴的惯性矩分别为As和Is(见图1).记砖砌体的弹性模量和剪切模量分别为Ec和Gc,泊松比为νc,剪切修正系数为kc;钢梁的弹性模量和剪切模量分别为Es和Gs,泊松比为νs,剪切修正系数为ks.假定在荷载q的作用下,钢梁-砖砌体组合梁的弯曲变形满足Timoshenko梁变形假定[13],且变形过程中钢梁和砖砌体通过螺栓协同工作.

图1 砖墙和钢梁组合截面Fig.1 Composite cross-section of brick wall and steel beam

图2 均布荷载作用下两端固支钢-砖组合梁Fig.2 Clamped steel-brick composite beam subjected to a uniform load

若钢梁-砖砌体组合梁变形后的挠度为w(x),横截面转角为θ(x),则组合梁横截面上钢梁和砖砌体的正应力分别为

于是,横截面上钢梁和砖砌体的弯矩Ms和Mc分别为

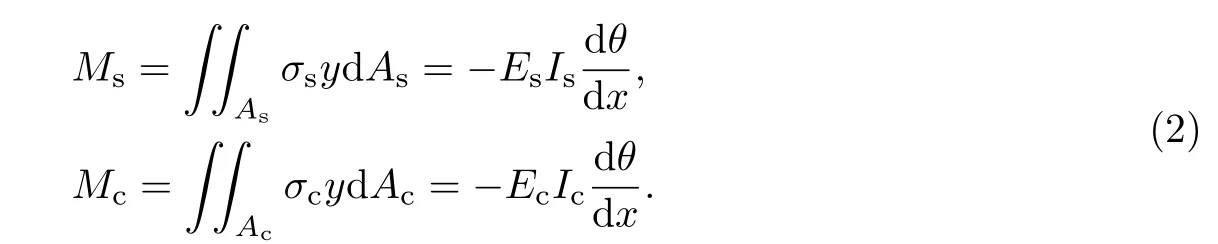
而组合梁横截面上的总弯矩为

式中,(EI)e=EcIc+2EsIs为钢梁-砖砌体组合梁的等效抗弯刚度.

记钢梁-砖砌体组合梁横截面上钢梁和砖砌体的剪力分别为Fs和Fc,则总剪力F为

记钢梁-砖砌体组合梁横截面的等效剪切刚度为(GA)e=GcAc+2GsAs,若记其等效剪切修正系数为k,则总剪力F为

在均布荷载q的作用下,钢梁-砖砌体组合梁弯曲变形的平衡方程为

于是,由方程(3),(5)和(6)可得钢梁-砖砌体Timoshenko组合梁弯曲变形的控制方程为

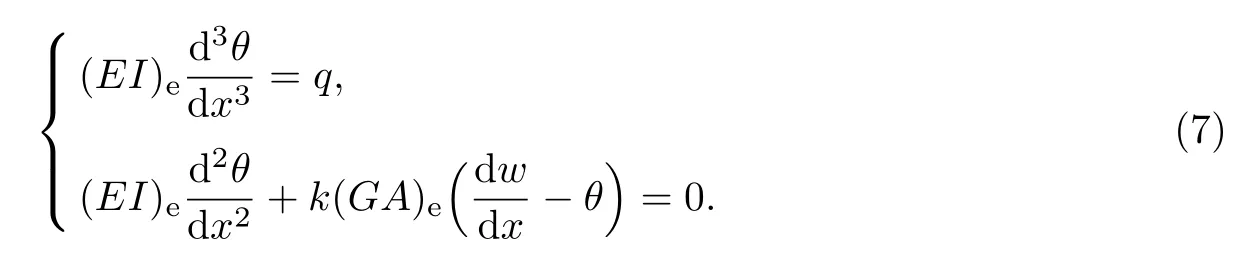
而边界条件为

显然,钢梁和砖砌体承担的荷载qs和qc分别为

不难得到边值问题(7)和(8)的解为

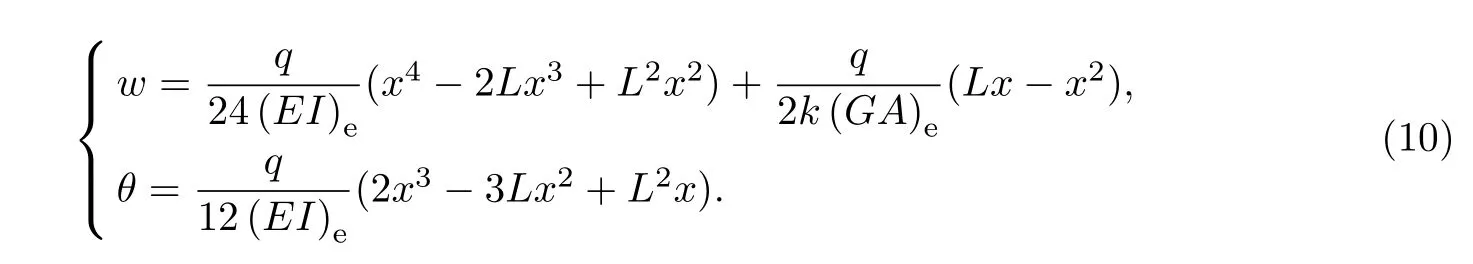
显然,当等效剪切刚度(GA)e→∞时,式(10)的结果趋于Euler组合梁的结果,即

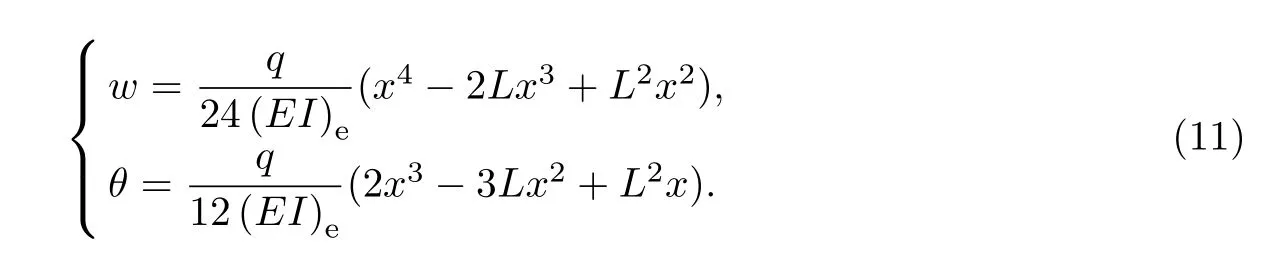
于是,由式(1)可得横截面上钢梁和砖砌体的正应力分别为

而横截面上钢梁和砖砌体的剪力分别为

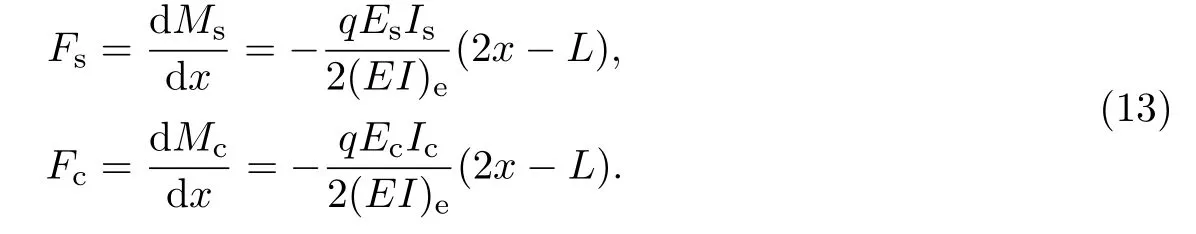
利用材料力学标准方法[13],可得钢梁-砖砌体Timoshenko组合梁横截面上钢梁和砖砌体的剪应力τs和τc分别为

由于木块与砖砌体间的摩擦系数大于木块与钢梁间的摩擦系数,因此为保证钢梁-砖砌体组合梁协同工作,设若木块和钢梁接触面的摩擦系数为µ,则钢梁-砖砌体组合梁单位长度的紧箍压力N满足

钢梁-砖砌体组合梁微元段dx的剪切应变能为

注意到

得到钢梁-砖砌体组合梁的等效剪切修正系数为

考虑砖砌体变形的拱效应,同时简化计算,根据文献[14]的规定,砖砌体计算高度：当高度大于钢-砖组合梁长L时,取砖砌体计算高度为L以考虑砖砌体变形的拱效应.考虑到本研究中的砌体建筑物砖墙高度为15 m,分析时取砖墙高度为钢梁-砖砌体组合梁长L.若砖墙容重为γc,则均布荷载q为

2 工字钢夹梁的参数分析

若采用I63c热轧普通工字钢作为砖墙基础托换的夹梁,由实验测定的该历史保护建筑砖墙以及I63c热轧普通工字钢的材料和几何参数如表1和2[15]所示,有

表1 钢梁和砖墙的材料参数Table 1 Material parameters of steel beam and brick masonry

表2 组合梁的横截面几何参数Table 2 Geometry parameters of cross section of composite beam

由文献[16]可知,砖墙形成矩形截面梁的剪切修正系数为

而工字钢截面的剪切修正系数为

式中,

于是,由式(21),(22)和(18)可得

由式(10)可得,当x=L/2时,钢梁-砖砌体组合梁的最大挠度为

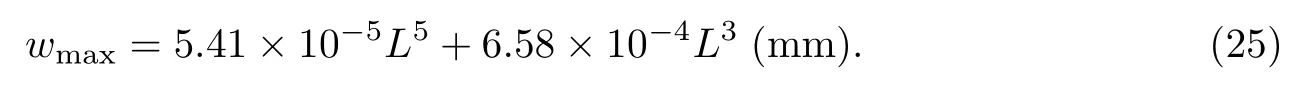
而由式(12)可得,当x=0,y=h/2时,钢梁-砖砌体组合梁中钢梁正应力σs的最大值和最小值分别为

同理,砖砌体正应力σc的最大值和最小值分别为

由于

由式(13)可得,当x=0或x=L时,Fs和Fc取最大值,从而由式(14)可得最大剪应力为

为得到该历史保护建筑砖墙基础单段托换的最大长度Lmax,记钢梁和砖砌体的许用正应力分别为[σs]和[σc],而其许用剪应力分别为[τs]和[τc],则由式(26)～(29)可得

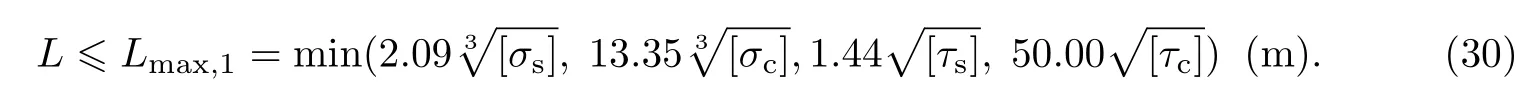
若钢梁-砖砌体组合梁的许用挠度为[w],则由式(25),要求

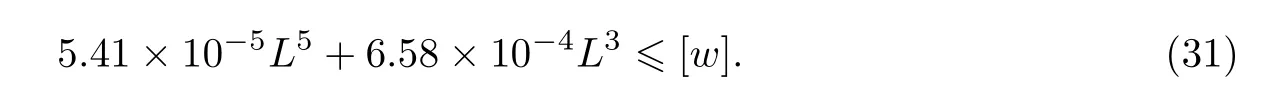
当L＞11 m时,式(31)第二项引起的误差小于9%,从工程施工角度可以忽略,从而有

由此可得

当L≤11 m时,式(31)难以得到解析解,为此附录A给出了最大挠度随组合梁长L的响应.对于给定的许用挠度[w],可由附录A确定当L≤11 m时的最大梁长Lmax,2.于是,考虑刚度和强度限制的最大托换长度Lmax为

同时,由式(9)可得qs=8.5L(kN/m).于是,由式(15)可得钢梁-砖砌体组合梁单位长度的紧箍压力应满足

类似地,根据I50a和I40a型热轧普通工字钢的材料和几何参数[15],可得到将I50a和I40a型热轧普通工字钢作为钢夹梁时,钢梁-砖砌体组合梁的最大挠度、最大正应力和剪应力与组合梁长L的关系,以及基础单段托换的最大长度Lmax,相关结果以及上述I63c型热轧普通工字钢的结果列于表3和附录A中.可见,随着工字钢型号编号的增加,钢梁-砖砌体组合梁的强度提高且刚度增大.对于给定长度L的钢梁-砖砌体组合梁,其最大挠度、最大钢梁正应力、最大砖墙正应力、最大钢梁剪应力和最大砖墙剪应力均减小,而钢梁承担的荷载以及锚栓承担的紧固压力不变.

表3 不同型号工字钢梁的钢-砖组合梁的最大挠度、最大应力、钢梁荷载及紧箍压力Table 3 Maximum de fl ections,maximum stresses,steel beam loads and con fi ning pressure of the steel-brick composite beam for di ff erent H-type steel beams

同时,可将钢梁-砖砌体组合梁等效为经典Euler组合梁进行分析.对于I63c型工字钢构成的钢梁-砖砌体组合梁,Timoshenko模型组合梁和Euler模型组合梁的挠度、应力等如表4所示.可见,Timoshenko模型的组合梁挠度大于Euler模型,相对误差为12.17/L2,即与梁长L的平方成反比,组合梁越长,二者相差越小.并且,最大钢梁正应力、最大砖墙正应力、最大钢梁剪应力、最大砖墙剪应力、钢梁承担的荷载以及锚栓承担的压力不变.因此,在基础托换设计中,对于强度控制问题,可采用简单的Euler组合梁进行分析和设计;而对于刚度控制问题,则建议采用Timoshenko组合梁进行分析和设计.

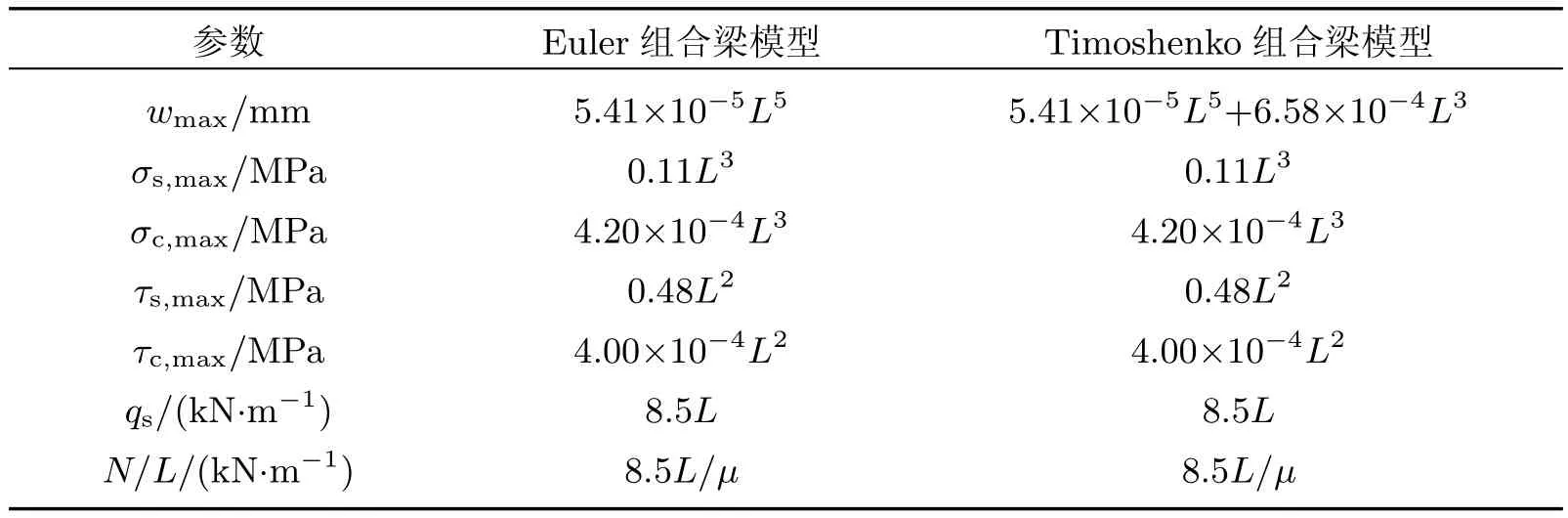
表4 I63c型工字钢梁-砖组合梁的Timoshenko模型和Euler模型的最大挠度、最大应力、钢梁荷载及紧箍压力对比Table 4 Maximum de fl ections,maximum stresses,steel beam loads and con fi ning pressure comparisons for Timoshenko model and Euler model of the I63c steel-brick composite beam

3 结论

本工作从理论上研究了采用钢夹梁进行砖墙基础托换的问题,将钢夹梁及钢梁间的砖砌体等效为Timoshenko组合梁,建立了弯曲变形控制方程,给出了基础单段托换时钢梁-砖砌体组合梁弯曲变形的解析解.具体分析了采用不同型号工字钢作为夹梁的钢梁-砖砌体组合梁最大挠度和最大应力等参数随基础单段托换长度的响应.根据强度和刚度条件,确定了基础单段托换的最大长度,并与Euler组合梁模型的相应结果进行了对比,得到如下结论.

(1)考虑拱效应时,在相同梁长情况下,随着工字钢型号编号的增加,钢梁-砖砌体组合梁最大挠度、最大钢梁正应力、最大砖墙正应力、最大钢梁剪应力和最大砖墙剪应力均减小,而钢梁承担的荷载以及锚栓承担的压力不变.

(2)在相同梁长情况下,Timoshenko模型的组合梁挠度大于Euler模型,二者的差随组合梁长的增大而减小,但两种模型的应力及锚栓承担的压力相同.

(3)在砖墙基础托换设计中,对于强度控制问题,可采用简单的Euler组合梁进行分析和设计;而对于刚度控制问题,建议采用Timoshenko组合梁进行分析和设计.

[1]张立人,卫海.建筑结构检测、鉴定与加固[M].武汉：武汉理工大学出版社,2012.

[2]欧阳煜,刘能科.外包钢加固轴心受压砖柱的受力性能分析[J].建筑结构,2006,36(11)：27-29.

[3]欧阳煜,龚勇.碳纤维布加固破损木柱偏心荷载作用下的性能试验[J].上海大学学报：自然科学版, 2012,18(2)：209-213.

[4]CORRADI M,BORRI A,GRAzINI A.Con fi nement of brick masonry columns with CFRP materials[J].Composites Science and Technology,2007,67(9)：1772-1783.

[5]ALHAYEK H,SvECOvA D.Flexural sti ff ness and strength of GFRP-reinforced timber beams[J]. Journal of Composites for Construction,2012,16(3)：245-252.

[6]卢欣,杨骁,宋少沪.纤维增强聚合物布加固木梁的非线性弯曲分析[J].上海大学学报：自然科学版,2012,18(6)：634-639.

[7]HARDY S J.Design of steel lintels supporting masonry walls[J].Engineering Structures,2000, 22(6)：597-604.

[8]MARIA E S,VAGELIs B L.Dynamic analysis of a masonry wall with reinforced concrete lintels or tie-beams[J].Engineering Structures,2012,44(11)：23-33.

[9]童敏,彭少民.钢-砌体组合结构在砖混建筑改造中的应用[J].武汉理工大学学报,2007,29(S2)：152-156.

[10]赵考重,王莉,夏风敏.钢-混组合结构在砖混建筑拆墙改造中的应用[J].建筑结构,2003,33(4)：28-35.

[11]敬登虎,曹双寅,石磊,等.钢板-砖砌体组合梁、柱静载下性能试验研究[J].土木工程学报,2010, 43(6)：48-56.

[12]敬登虎,曹双寅,郭华忠.钢板-砖砌体组合结构托换改造技术及应用[J].土木工程学报,2009,42(5)：55-60.

[13]GERE J M,TIMOsHENKO S P.Mechanics of materials[M].2nd ed.New York：Van Nostrand Reinhold,1984.

[14]中国建筑东北设计研究院有限公司.GB 50003—2011砌体结构设计规范[S].北京：中国建筑工业出版社,2011.

[15]沈祖炎,陈扬骥,陈以一.钢结构基本原理[M].北京：中国建筑工业出版社,2005.

[16]COwPER G R.The shear coefficient in Timoshenko’s beam theory[J].Journal of Applied Mechanics,1966,33(2)：335-340.

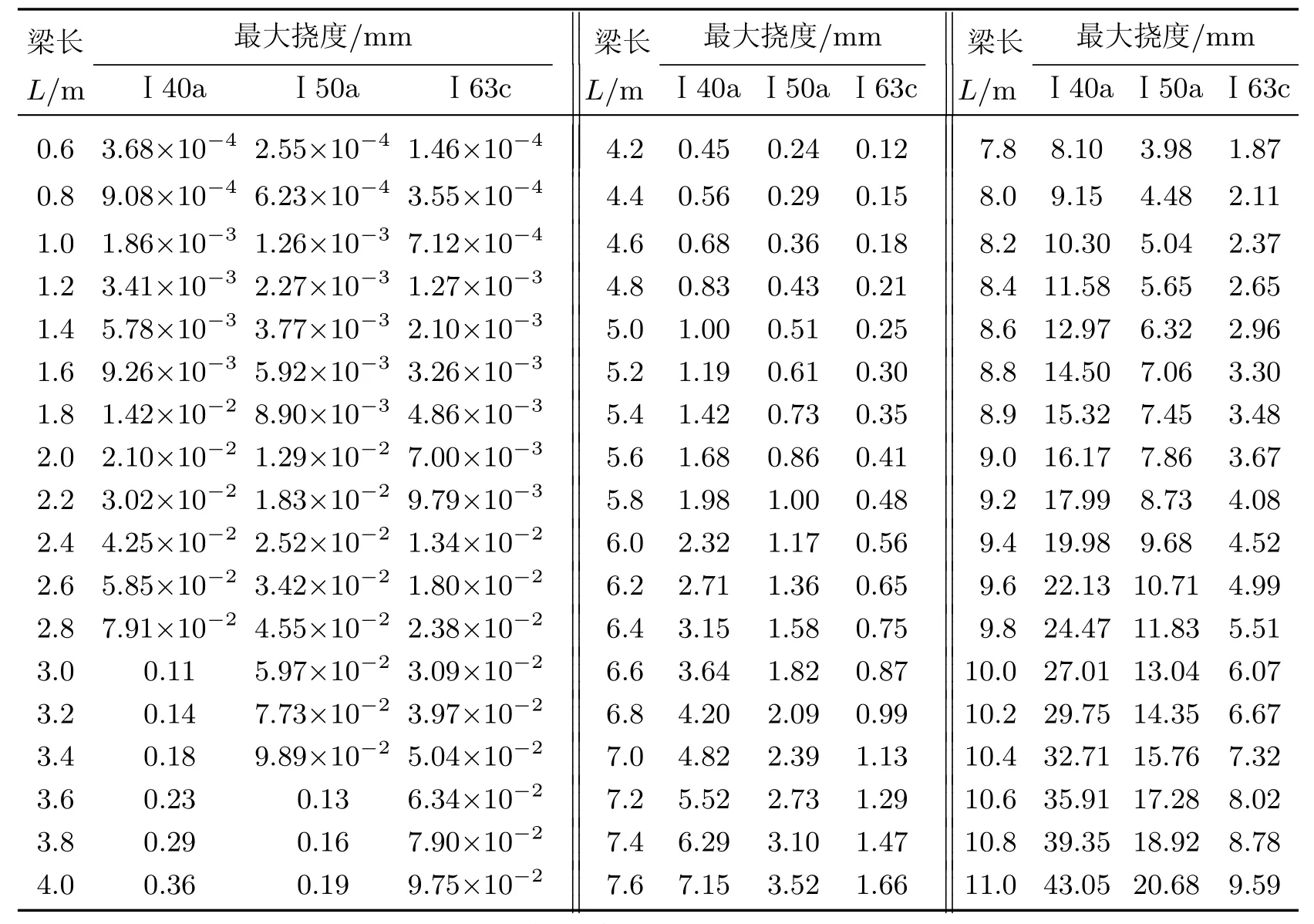
附录A 考虑拱效应时工字钢-砖砌体组合梁最大挠度梁长的响应

本文彩色版可登陆本刊网站查询：http：//www.journal.shu.edu.cn

Timoshenko composite beam model analysis of steel beam and brick masonry for foundation underpinning of masonry wall

XIANG Xiao-xiao,WU Li-wei,YANG Xiao
(Department of Civil Engineering,Shanghai University,Shanghai 200072,China)

Regarding the steel clamping beams and brick masonry between them as a composite beam and based on the Timoshenko elastic beam model,the governing equation for bending deformation of composite beam is established.The analytical solution for bending deformation of the composite beam of steel and brick masonry is presented.Considering the arch e ff ect of the brick masonry,the foundation underpinning of the brick wall of masonry structure is investigated.The maximum de fl ection and maximum stresses of the steel-brick masonry composite beam for di ff erent models of H-type steel clamping beam are obtained,and the maximum length of the foundation underpinning for single stage is given.It is shown that de fl ection and stresses of the steel-brick masonry composite beam decrease with the model number of the H-type steel beam increasing,but the load held by the steel beam and the con fi ning pressure of the steel-brick masonry composite beam are unchanged.Furthermore,the de fl ection of the Timoshenko composite beam is larger than that of the Euler composite beam,but the stresses and con fi ning pressure are the same.Therefore,in the foundation underpinning design,the model of an Euler composite beam can be used for strength analysis,and the Timoshenko composite beam model can be used for sti ff ness analysis.

brick masonry;foundation underpinning;composite beam;arch e ff ect; underpinning length

TU 362;TU 398.9

A

1007-2861(2015)01-0097-09

10.3969/j.issn.1007-2861.2014.01.011

2014-01-22

国家高技术研究发展计划(863计划)资助项目(2009AA0323032)

杨 骁(1965—),男,教授,博士生导师,博士,研究方向为土-桩结构相互作用、流固耦合作用. E-mail：xyang@shu.edu.cn