曲线的副法线曲面及其性质研究*

梁林

（楚雄师范学院数学与统计学院，云南 楚雄 675000）

曲线的副法线曲面及其性质研究*

梁林

（楚雄师范学院数学与统计学院，云南 楚雄 675000）

摘要：通过类比一般空间曲线、曲面的研究方法，讨论了三维欧氏空间中曲线的副法线曲面，给出了副法线曲面的渐近线和曲率线；再由高斯曲率、平均曲率，得到了副法线曲面上常高斯曲率曲线、极小轨迹；最后，利用高斯曲率和平均曲率之间的线性关系和平方关系，得到了副法线曲面的分类定理。

关键词：副法线曲面；高斯曲率；极小轨迹；主曲率

曲面是经典微分几何研究的主要对象，它有许多丰富的性质，而微分几何学家常致力于一些特殊曲面的研究，以期扩宽曲面的知识。文献［1］讨论了三维欧氏空间中特殊曲线的主法线曲面。根据渐近曲线的方程，具体给出主法线曲面的一族非直线的渐近曲线，再根据平均曲率、高斯曲率及主曲率函数，得到曲线的主法线曲面的极小轨迹、常高斯曲率曲线及两个主曲率函数之比为常数的曲线，还给出了曲面上测地线和腰曲线的性质.本文利用类比的研究方法，讨论了三维欧氏空间中曲线的副法线曲面，获得了副法线曲面的渐近线和曲率线、常高斯曲率曲线、极小轨迹以及副法线曲面的分类定理。由于副法线曲面属于可展曲面的范畴，因此对副法线曲面的研究可丰富可展曲面的相关内容。

1.　预备知识

相应地，曲面的第一基本形式、单位法向量、第二基本形式、高斯曲率、平均曲率和两个主曲率函数分别由（1.2）-（1.7）给出：

2.　主要结论

2.1副法线曲面的渐近曲线和曲率线

根据渐近曲线和曲率线方程得到下面定理：

其中c1为常数。

证明副法线曲面的渐近线曲线方程为

化简得

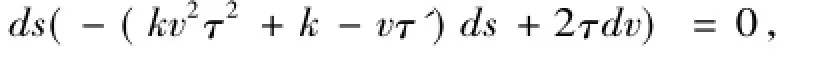
即

所以渐近线方程为

定义2.1.3［1］在三维欧氏空间中，如果两条空间曲线Γ和Γ1之间建立这样一种关系，使得在对应点上Γ的主法线和Γ1的副法线重合，则称Γ为Mannheim曲线，Γ1为Mannheim侣线，（Γ，Γ1）称为Mannheim侣线对。

引理2.1.4［1］一条空间曲线为Mannheim曲线的充分必要条件是其曲率和挠率满足k=λ（k2+τ2），其中λ为非零常数.

定理2.1.5在Mannheim曲线Γ的副法线曲面上，其一族非直线的渐近曲线方程为

定义2.1.6［1］如果曲线Γ和Γ1之间建立这样的一一对应关系，使得在对应点的主法线重合，则这两条曲线都称为Bertrand曲线，其中每一条称为另一条的侣线。

引理2.1.7［1］一条空间曲线为Bertrand曲线的充分必要条件是其曲率和挠率满足λk+uτ= 1，其中λ，τ为常数，而且λ≠0.

定理2.1.8在Bertrand曲线Γ的副法线曲面上，其一族非直线的渐近曲线方程为

证明曲线为曲纹坐标网的充要条件为L=N=0，由（1.4）得kv2τ2+k-vτ′=0，从而有

定理2. 1. 10 Mannheim 曲线的副法线曲面的曲纹坐标网是渐近网的充分必要条件是

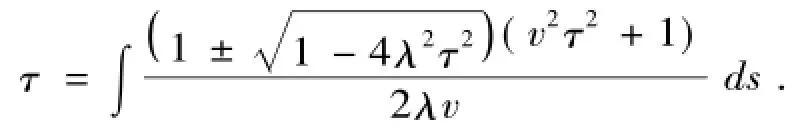
定理2.1.11Bertrand曲线的副法线曲面的曲纹坐标网是渐近网的充分必要条件是

其中，k，τ分别为曲线r→（s）的曲率和挠率。

证明副法线曲面的曲率线方程为

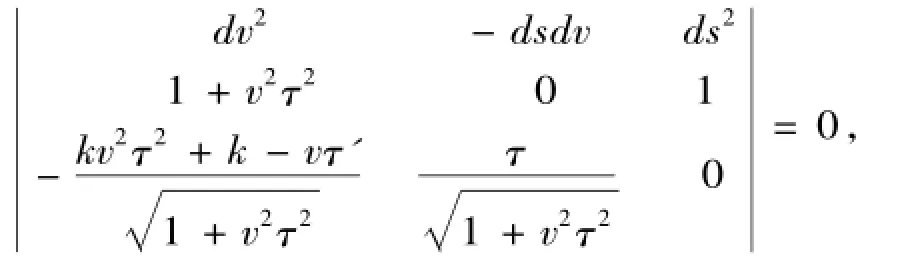
化简得

从而

推论2.1.14当λ＞0时，Mannheim曲线的副法线曲面的曲率线方程为

推论2.1.15Bertrand曲线的副法线曲面的曲率线方程为

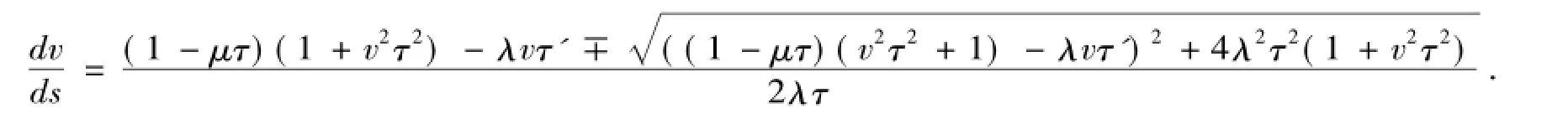
2.2副法线曲面上常高斯曲率曲线

证明设高斯曲率K=-a2，下面不妨取τ＞0，此时由（1.5）有

即

所以

从而常高斯曲率曲线为

引理2.2.3［3］一条空间曲线为一般螺线的充分必要条件是它的曲率和挠率之比为常数。

由引理2.2.3可看出推论2.2.5是定理2.2.4的直接结论。

2.3副法线曲面的极小轨迹

其中，k，τ分别为r→（s）的曲率和挠率。

证明设副法线曲面的极小轨迹为

由（1.6）式及平均曲率的定义，有

即

从而有

所以副法线曲面的极小轨迹为

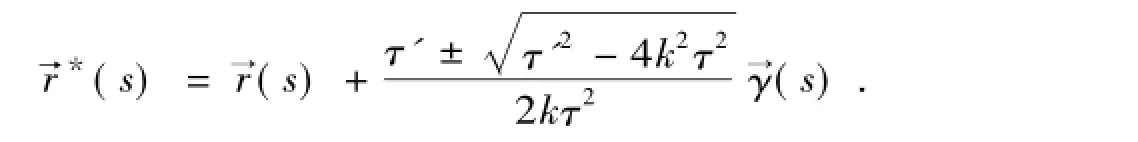
2.4 Weingarten型副法线曲面

定义2.4.1［4］若曲面S的Gauss曲率K和平均曲率H满足函数关系式f（H，K）=0，则称曲面S为Weingarten型曲面或Weingarten曲面。

定理2.4.3不存在高斯曲率为非零常数的副法线曲面。

上式是关于v的多项式，则

即c=τ=0，矛盾，定理得证。

则

所以k=0且τ=常数，从而曲面为平面。

用类似的方法，可以得到定理（2.4.5）—定理（2.4.8）.

参考文献：

［1］袁媛，刘会立.曲线的主法线曲面 ［J］.东北大学学报 （自然科学版），2007，28 （01）：145-148.

［2］梅向明，黄敬之.微分几何［M］.北京：高等教育出版社，2008.

［3］陈维桓.微分几何［M］.北京大学出版社，2006.

［4］袁媛，张金亮，李春秀，刘会立.三维Minkowski空间中的平移曲面［J］.东北大学学报，2009（02）：302-304.

（责任编辑李艳梅）

中图分类号：O186.1

文章标识码：A

文章编号：1671-7406（2015）03-0001-05

*基金项目：楚雄师范学院国家自然科学基金孵化项目。

收稿日期：2015-01-12

作者简介：梁林 （1967—），男，硕士生导师，教授，研究方向：微分几何及其应用。

Research on the Binormal Surfaces of Curves and Their Properties

LIANG Lin
（School of Mathematics&Statistics，Chuxiong Normal University，Chuxiong，675000，Yunnan Province）

Abstract：By analogy to the research methods on the general space curves and surfaces，We discussed the binormal surfaces，and get the asymptotic curves and curvature.Then，based on the Gaussian curvature and the mean curvature，the curves with constant Gaussian curvature and minimal locus are obtained. It follows that some theorems of classification of those binormal surfaces are given by virtue of the linear and square relationships between the Gaussian curvature and the mean curvature.

Key words：binormal surfaces；Gaussian curvature；minimal locus；principal curvature