Geogebra与三角函数图象变换整合案例

殷羽

摘 要 GeoGebra是一款动态数学软件，可以全面应用于中小学数学各分支和各阶段的教学。案例介绍了geogebra在高中三角函数教学中的整合应用。

关键词 geogebra 数形结合 整合 学习兴趣

中图分类号：G633.6 文献标识码：A 文章编号：1002-7661（ 2015 ）07-0001-01

函数f=sinx与g=Asin （ωx+φ）+C图象变换在Geogebra中很容易实现动态演示和学生实际操作。在学f= sinx图像和性质后，学生通过亲自体会f=sinx与g=Asin（ωx+φ）+C图象变换过程，探讨A、ω、φ、C对图像的影响，实现教师由教学向导学的角色的转变。

1.打开Geogebra，把查看菜单栏坐标轴显示出来，并设置主绘图区X辅间距为π/2，Y轴间距为1。代数定义区输入f（x）=siri（x），画出正弦函数图像，设置函数f属性。

2.分别添加动作对象工具滑杆A、ω、φ、C，点工具栏上的滑杆按钮，在偏右上角按住鼠标拉出滑杆，设置滑杆属性名称为A，间直为-5到5。依次新建出ω、φ、C滑杆。

3.添加动作对象工具中对象群组隐藏或显示按钮a.b、c、d、e五个按钮。新建按钮a：点工具栏上的对象群组隐藏或显示按钮，标签文字为“显示y=smx”、名称为a的按钮。依次新建名称为b、标签文字为“显示y=A sinx”按钮；名称为c、标签文字为“显示y=A*sin（ωx）”按钮；名称为d、标签文字为“显示v=A sin（ωx+φ）”按钮；名称为e、标签文字为“显示y=A sinωx+φ）+C”按钮；通过点选这五个按钮，可以分别显示对应函数。

4.新建高级对象工具中text1、text2、text3、text4、text5五个文本框。分别在文本框中显示A、ω、φ、C四个参数通过移动滑杆后在函数中的值。新建text5：插入text5，设置文本框属性时，在文本框中输入“A-”对象选项中A、“ω=”对象选项中ω、“φ=”对象选项中φ、“C=”对象选项中C。设置text5属性中高级选项中的显示对象的条件为e，只有在显示y=Asin（ωx+φ）+C图像时，对应的参数才显示在按钮后面。

5.在代数定义区分别输入g （x） =A*sin （x）、h（x） =A*sin（ω*x）、i（x）=A*sin（ω*x+φ）、j（x）=A*sin（ω*x+φ+C函数，绘图区显示出函数图像，更改函数图像性质，分别设置图像颜色、线样式等，使函数之间有明显的区分。并在代数区分别设置函数f、g、h、i、j，属性中高级选项中的显示对象的条件分别为a、b、c、d、e。

6.通过以上步骤作出了方便学生操作和探究的函数f=smx与g=Asin（ωx+φ）+C图象变换的GGB程序界面，可以让学生探究A、ω、φ、C四个参数对函数图像的影响，让参数“动起来”，从而使图象动起来，在变化的过程中总结规律，体现了基本的解决数学问题的思想方法。

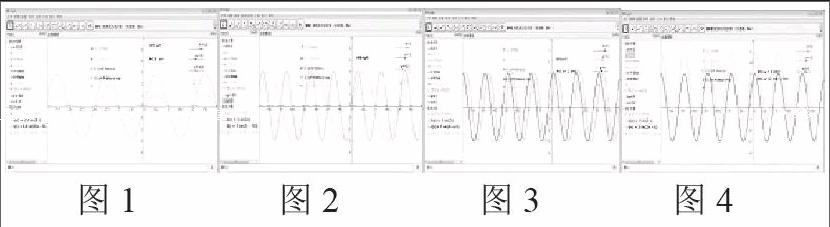
7.分成四组分别探究A、ω、φ、C四个参数对函数图像的影响。第‘组探究A对函数图像的影响：第一勾选“显示y=smx”按钮，在作图区显示y=smx正弦，第二勾选“显示y=As-mx”按钮，在作图区显示y=Asinx正弦，第三移动A滑杆，在移动滑杆时学生认真观察并作记录，如图1

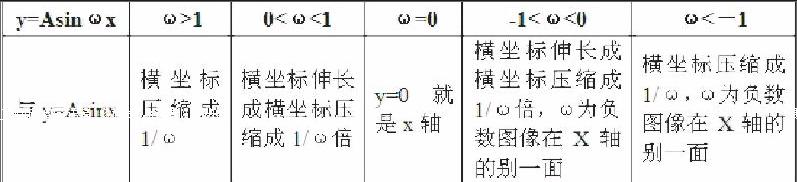
第二组探究（1）对函数图像的影响：第'匈选“显示y=Asin-x”按钮，在作图区显示y=Asinx图像，第二勾选“显示y=Asinωx”按钮，在作图区显示y=Asinωx图像，第三移动ω滑杆，在移动滑秆时学生认真观察并作记录，如图2

第三组探究φ对函数图像的影响：第一勾选“显示y=A*sin（ωx）”按钮，在作图区显示y=A*sin（ωx）图像，第二勾选“显示V=A sin（ωx+φ）”按钮，在作图区显示V=A sin（ωx+φ）图像，第三移动φ滑杆，在移动滑杆时学生认真观察并作记录。如图3

第四组探究C对函数图像的影响：第‘勾选“显示y=Asin（ωx+φ）”按钮，在作图区显示v=A sin（ωx+φ）图像，第二勾选“显示y=A sin（ωx+φ）+C”按钮，在作图区显示y=A sin（ωx+ φ）+C图像，第三移动C滑杆，在移动滑杆时学生认真观察并作记录。如图4

根据自己的教学意图，随心所欲地修改解析式的参数，并且能让图象真正“动”起来，给学生的学习创设‘个体验和理解数学的过程，使学生直观感受到数形结合是探寻数学规律的绝佳方法。达到新课程下研究性学习的目的，最终提高了教与学的双重效率。