Output Feedback Dynamic Surface Controller Design for Airbreathing Hypersonic Flight Vehicle
2015-08-09DelongHouQingWangandChaoyangDong
Delong Hou,Qing Wang,and Chaoyang Dong
Output Feedback Dynamic Surface Controller Design for Airbreathing Hypersonic Flight Vehicle
Delong Hou,Qing Wang,and Chaoyang Dong
—This paper addresses issues related to nonlinear robust output feedback controller design for a nonlinear model of airbreathing hypersonic vehicle.The control objective is to realize robust tracking of velocity and altitude in the presence of immeasurable states,uncertainties and varying fl ight conditions. A novel reduced order fuzzy observer is proposed to estimate the immeasurable states.Based on the information of observer and the measured states,a new robust output feedback controller combining dynamic surface theory and fuzzy logic system is proposed for airbreathing hypersonic vehicle.The closedloop system is proved to be semi-globally uniformly ultimately bounded(SUUB),and the tracking error can be made small enough by choosing proper gains of the controller, fi lter and observer.Simulation results from the full nonlinear vehicle model illustrate the effectiveness and good performance of the proposed control scheme.
Index Terms—Hypersonic fl ight vehicle,immeasurable states, output feedback control,model uncertainties,fuzzy logic system, dynamic surface control.
I.INTRODUCTION
AIRBREATHING hypersonic vehicles(AHVs)have been studied broadly due to the prospects of high speed transportation and affordable space access for a long time.For the purpose of fl ight safety and high accuracy,control system design has become a core problem for AHV.However,the following characteristics of AHV make this problem full of challenges[1-5].
1)There are strong couplings between propulsive and aerodynamic forces,which are caused by the integrated confi guration of the airframe and the scramjet engine.
2)The uncertainties of aerodynamic parameters[1]are derived from large-scale variations of altitude and velocity.
3)The immeasurable states exist in hypersonic condition.
In the past decades,amounts of work has been done for developing control system of hypersonic fl ight vehicle.Mainly, the control system design can be classi fi ed into two categories based on the linear and nonlinear models,respectively.For the controller design of the linearized dynamic models of hypersonic vehicles,several methods are adopted While considering the problems of different complexity,such as decentralized control[6],linear quadratic regulator(LQR)approach[7],gainscheduling method[8],etc.On the assumption that the fi ght dynamics at a certain point can be denoted by the linear combination of the model on adjacent design points,the linear parameter varying(LPV)model of hypersonic vehicle is proposed.Various methods are developed for LPV system of hypersonic vehicle[9-10].T-S fuzzy system based method is also adopted to synthesize controller for hypersonic vehicle based on linearized dynamical model[11].Linearized dynamical model for hypersonic vehicle is obtained through Jacobian linearization under certain conditions,which brings loss of dynamic characteristic to some degree.
Actually,the hypersonic fl ight vehicle is a nonlinear system,and the controllers based on nonlinear model are more accurate than the linear.The nonlinear methods include feedback linearization[12-13],sliding mode[14-15],etc.Feedback linearization requires repetitive differentiations of system nonlinear terms,which is dif fi cult to achieve in real world.Sliding mode method is easy to cause chattering of the input.At present,as a kind of convenient control design method for strict feedback nonlinear system,backstepping has received a lot of research attention for applications in hypersonic vehicle control area[16-17].
However,the methods mentioned above require full information of the states,which limits their practical applications. In fact,the angle of attack(AOA)is dif fi cult to be measured in hypersonic condition.Hypersonic aerodynamic heating decline the performance of the commonly used air-data sensors.Flush air-data sensor(FADS)is another instrument for AOA measurement,but when used in hypersonic condition,modeling of aerodynamic heating process is also a hard task,which is the fundamental problem of FADS[2].
Observer-based output feedback control is a feasible method for hypersonic vehicle[2,13,18]in the presence of immeasurable states.In[13],a sliding mode observer(SMO)is used to construct the immeasurable states.However,the observer is developed based on the exactly known parameters in the dynamic equations.When there exist parameters uncertainties, the equilibrium point of this observer is not the origin,which brings steady estimation errors.Besides,the controller is designed based on feedback linearization and sliding mode control.However,complex derivative signals of altitude and velocity are essential,but unavailable.
Reference[18]proposes a kind of robust output feedback scheme for linearized hypersonic vehicle model.The information used in the controller only includes velocity,altitude, pitch rate and normal acceleration,while the required state signals in the nominal controller are replaced by the signals from the full state observer.
Reference[2]proposes an output feedback controller combining backstepping and sliding mode observer.The stability of the closed-loop system and the convergence of the outputtracking error are veri fi ed based on the small-gain theorem. However,parameter uncertainties are not considered,and the problem of“explosion of complexity”arising from the differentiation of the intermediate virtual control exists in[2]. Besides,the small-gain theorem holds only when tracking errors are out of certain range,so the stability proof is not complete.
A number of dif fi culties still exist in output feedback controller for hypersonic vehicle system.
1)The system cannot be exactly expressed in strict feedback form.
2)Forces and moment of hypersonic vehicle are the functions of AOA and its high order terms.
3)Altitude information cannot be used as unique information to estimate AOA because its precision is much lower than the measured values of pitch angle and pitch angle rate.
4)The aerodynamic coef fi cients are uncertain to some degree.
These four dif fi culties lead to the failure of commonly used high-gain observer or K- fi lter.Reference[19]solves a class of nonlinear systems output feedback tracking problem combining the modi fi ed high-gain observer and the adaptive backstepping controller,but the uncertainties are dominated by output-dependent functions,and the immeasurable states are constructed using the fi rst state information which is also the output variable.The virtual control coef fi cients in[19] are ones,which is another advantage of output feedback controller design.Reference[20]proposes an output feedback control scheme for a class of stochastic nonlinear systems combining a kind of full-order observer and backstepping approach,in which the virtual control gains are also ones. Output feedback control for stabilization problem of nonlinear system is summarized in[21].The control schemes above are not suitable for the hypersonic vehicle model.
In this paper,the objective is to construct a nonlinear output feedback tracking controller for hypersonic vehicle.The main contributions of this paper are summarized as follows.
1)The local characteristic of thrust and pitching moment with respect to AOA in the argument range is fi rst validated. The advantage of this characteristic is discussed in Remark 1.
2)A reduced order observer is fi rst proposed to estimate the value of immeasurable AOA based on the information of pitch angle and its rate.
3)The output feedback fuzzy dynamic surface technique[22]is fi rst adopted for hypersonic vehicle control,which drives the trajectories of the velocity and altitude tracking errors into an arbitrarily small neighborhood of the origin.Fuzzy logic system method is used to compensate the effects of parameter uncertainties.
Besides these contributions,continuous hyperbolic tangent function is used in the virtual and actual control design to eliminate the effect of fuzzy estimation.Numerical simulations of various situations are presented.The maneuver is performed under several conditions to demonstrate that the control laws are valid for the entire fl ight envelope.It is shown that trajectory control is established for the closed-loop system even in the presence of uncertainties and immeasurable states in the vehicle model.
The reminder of this paper is organized as follows.The hypersonic vehicle longitudinal motion model is described in Section II.In Section III,the fl ight control system for hypersonic vehicles adopting the fuzzy reduced order observer and fuzzy dynamic surface technique is addressed.A comprehensive stability analysis is given for the closed-loop system. In Section IV,numerical simulations on the longitudinal hypersonic vehicle model are carried out to validate the proposed controller.Finally,brief concluding remarks end the paper in Section V.
II.PLANT MODEL AND PROBLEM FORMULATION
The hypersonic vehicle model considered in this study is the curve- fi tted model(CFM)given by Fiorentini[16],where the complex forces and moment are approximated in curvefi tted form.The control inputs of this model are the elevator de fl ection angle and fuel-to-air ratio.The longitudinal dynamic equations are written as■
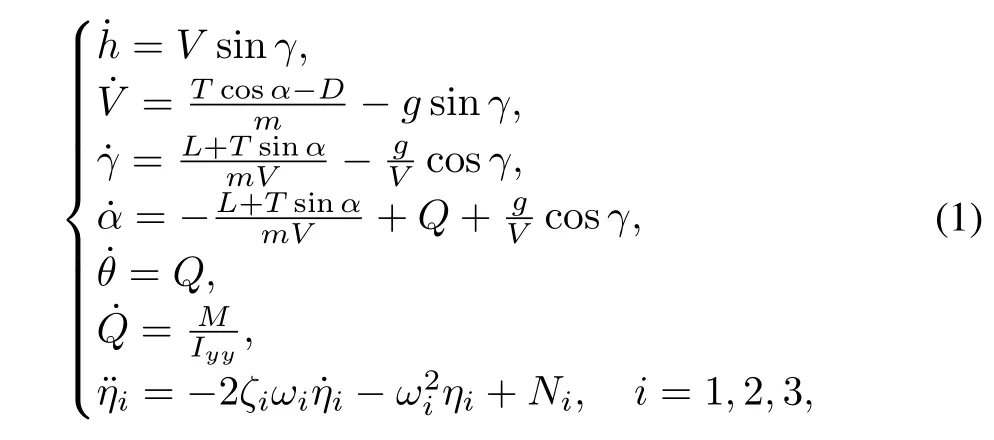
whereh,V,γ,α,θ,Qandηiare altitude,velocity, fl ight path angle(FPA),AOA,pitch angle,pitch rate and theith generalized elastic coordinate of the vehicle,respectively.T,D,L,MandNidenote thrust,drag,lift,pitching moment and theith generalized force,respectively.In the CFM,by de fi ningη=[η1η2η3]T,these forces and moment are approximated as follows:
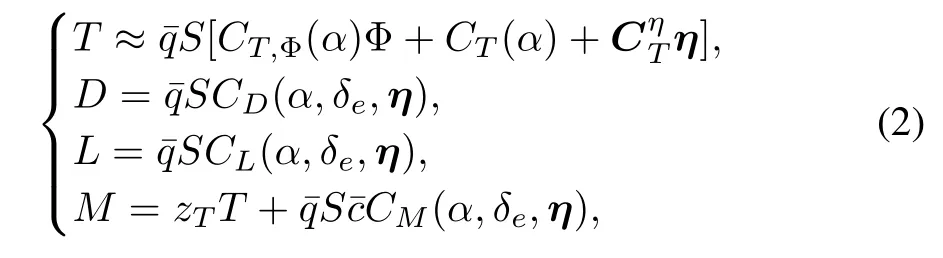

The rest of nomenclatures are revealed in Table I.The admissible ranges of states and inputs are displayed in Table II.
Remark 1.The CFM is derived from the true model (TM)in[3]by expressingT,L,D,Min the curve- fi tted form.This manner is similar to the method of Parker[23]. The CFM can depict the TM with suf fi cient accuracy.All the dominant features including the coupling between thrust and aerodynamic forces,the effect of the thrust(engine)on themoment,the fl exibility effect and the nonlinearity of force and moment are all retained in this model.Due to the lack of data for the TM,the CFM is taken as the simulation model to produce true states of AHV in this paper.The data of CFM can be found in[24].

TABLE I NOMENCLATURES OF HYPERSONIC VEHICLE

TABLE II ADMISSIBLE RANGES OF STATES,INPUTS,DYNAMIC ___________PRESSURE,AND MACH NUMBER
From equations(1)-(3),thrustTand momentMare expressed in nonlinear form.We calculateTfor different Φ andα,andMfor differentαwhile the elevator angle is the trim value,and the relationships are depicted in Figs.1 and 2.
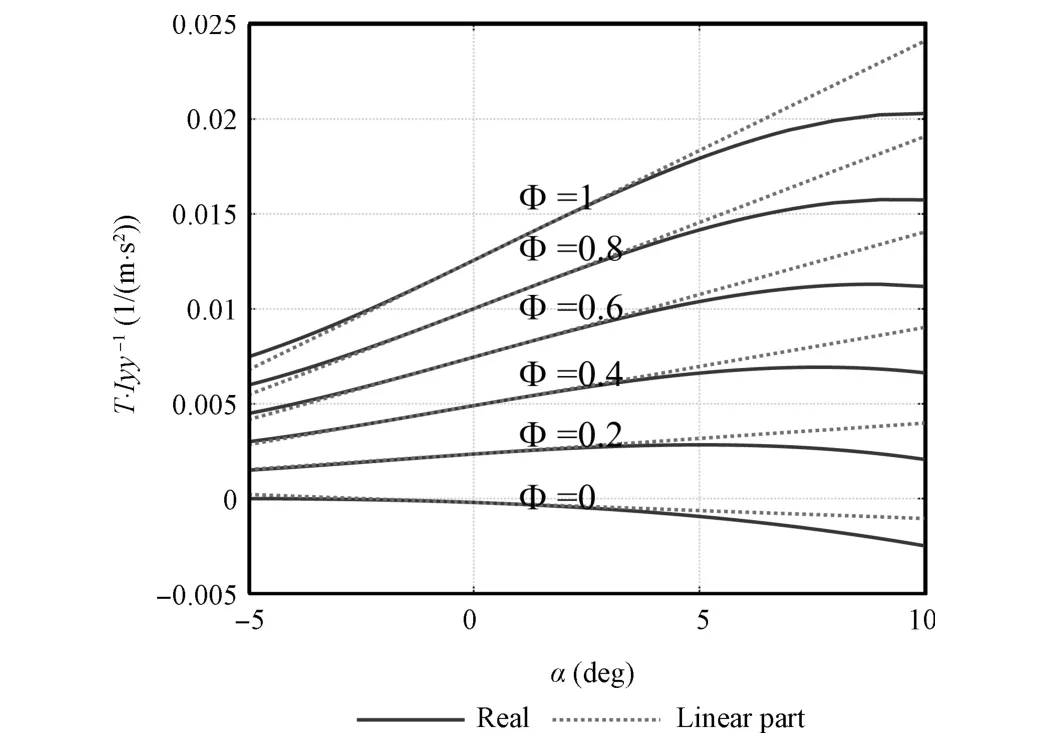
Fig.1.Tfor differentαand Φ.
It is obtained thatTandMsatisfy the locally Lipschitz condition with respect to AOA in the argument range according to Figs.1 and 2.Consequently,for the value of Φ andδein the admissible range,T(α,Φ)andM(α,δe)satisfy the Lipschitz condition with some Lipschitz constantsσTandσMas

where Ωαdenotes the argument range forαwhich is listed in Table II.
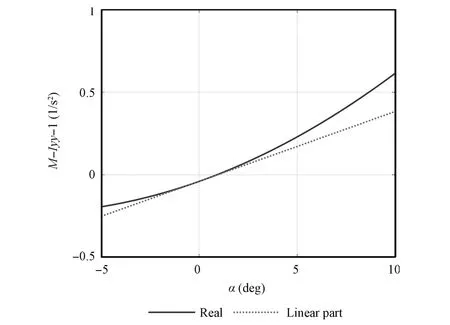
Fig.2.Mfor differentα.
According to(1),the velocity is mainly controlled by the throttle setting Φ,while the change of the altitude is governed by the elevator de fl ectionδe.Therefore,we separate the longitudinal dynamics into two subsystems,and design the velocity controller and altitude controller separately.The velocity is considered separately from the rest of dynamics, and the model is denoted as

wherefv=(α)cosα/m--gsinγ,gv(x1,x2,x3,V)=¯qSCT,Φ(α)cosα/m.
The rest of the hypersonic vehicle dynamic model constitutes the altitude tracking loop.The selected states for altitude loop are de fi ned as

The transformation of altitude is to keep all states in the same size scale.Due to the fact that cosγ≈1 ifγis small enough, the CFM of altitude loop can be transformed into
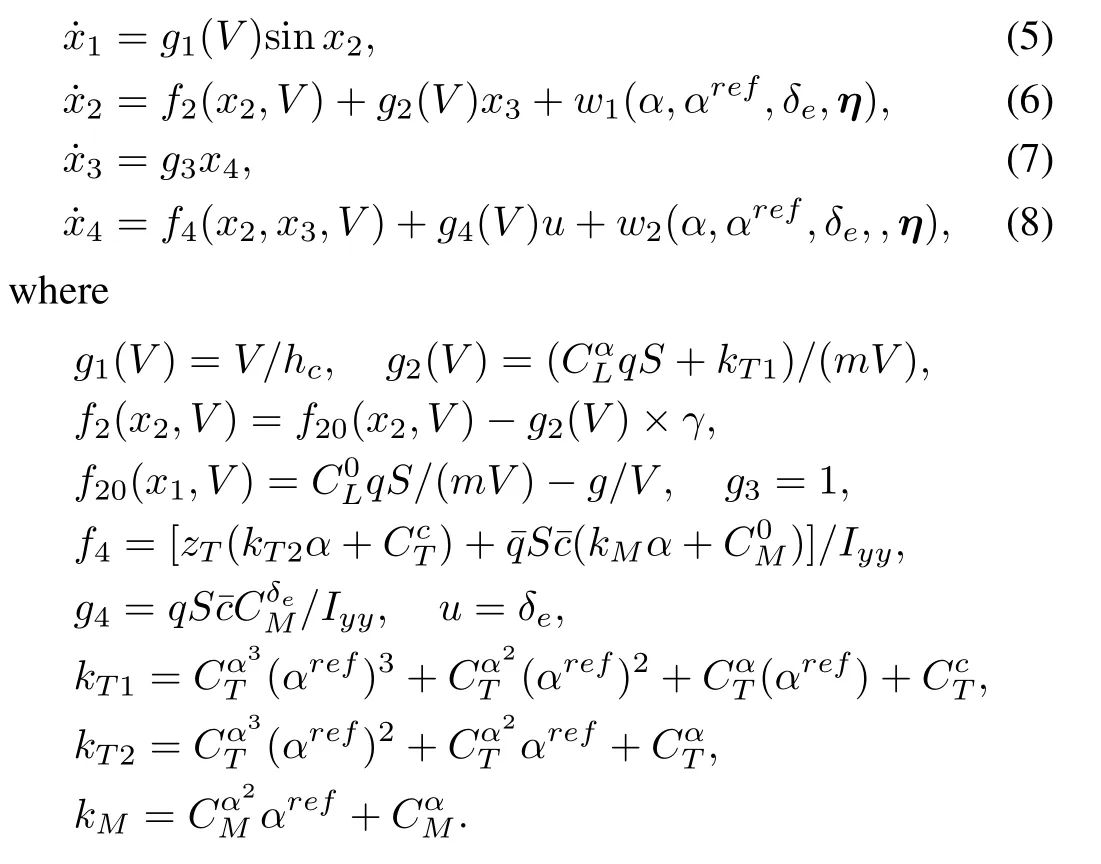
The goal of this study is to synthesize a controller using measurable state information realizing altitude and velocity tracking.
Remark 2.It can be concluded thatw1andw2are mainly constituted by three parts,namely,the difference betweenαrefandα,coef fi cient uncertainties and generalized elastic coordinates.From the locally Lipschitz characteristic ofTandM,we can obtain that the fi rst one can also be seen as coef fi cient uncertainty.
The following assumptions are made for developing the output feedback based control laws.
Assumption 1.The generalized elastic coordinate is mainly affected by AOA and is much less affected byδe.
Assumption 2.The reference signalhd(t)is a suf fi ciently smooth function oft,andhd(t),˙hd(t),¨hd(t)are bounded within a known compact set

III.OUTPUT FEEDBACK DYNAMIC SURFACE CONTROLLER
The strategy chosen here is an output feedback controller based on dynamic surface control(DSC).First a fuzzy reduced order observer is designed for altitude loop to estimate AOA. Simultaneously,the estimated value of FPA is obtained based on the value of pitch angle and estimated value of AOA.Then, the dynamic surface control is applied using the estimated value of FPA,pitch angle,pitch angle as virtual control inputs,and the estimation error of FPA and uncertainties are considered as disturbances whose behavior must be dominated.
A.Fuzzy Logic Systems and Reduced Order Observer Design for Altitude Loop
First we introduce the following useful lemma on fuzzy logic systems(FLSs).
Lemma 1[25].Letf(x)be a continuous function of vectorxde fi ned on a compact setU.Then for any constantε>0, there exists the following FLSs:

whereis the fuzzy membership function.
In the model presented in(1),γandαare two immeasurable states.Due to the relationship thatα=θ-γ,we only need to estimate one of them.We selectαas the variable to be estimated.De fi ningxb=[α,αref,δe,η]T,wi(α,αref,δe,η) (i=1,2)can be denoted asw1(xb)andw2(xb).According to Lemma 1,each unknown nonlinear uncertain functionˆwjcan be approximated by a FLS in the form of

wherey=[θ,q]Tis the measurable states vector,L=[l1,l2] is the observer gain coef fi cient matrix,and these gain coef ficients are de fi ned as

The stability of the estimation error is given by the following proposition.
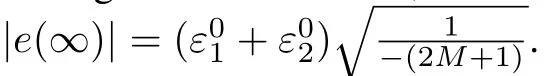
Proof.Consider the Lyapunov function candidate as

The derivative along the trajectory of(17)results in
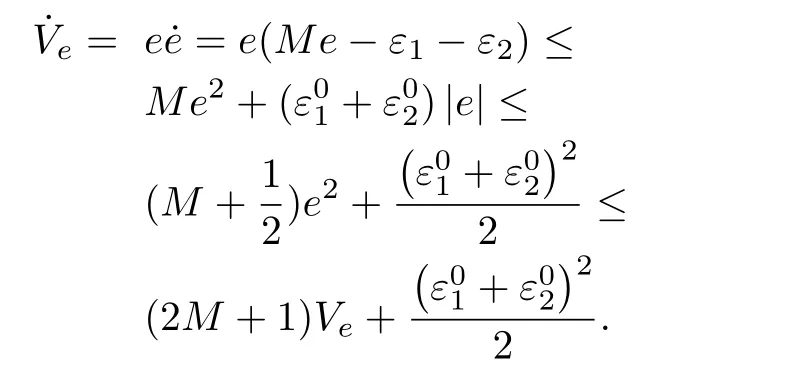
According to the differential inequality theory,there exists the following inequality by induction

B.Controller Design for Altitude Loop
In this section,an adaptive fuzzy controller and parameter adaptive laws are to be developed in the framework of the backstepping design and DSC technique so that all the signals in the closed-loop system are SUUB,and the tracking errors of altitude are as small as desired.
Step 1.De fi ne the dynamic surface error(tracking error)asz1:=x1-hd,whose time derivative while considering(5)is
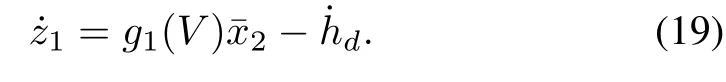
Although the precision of altitude signal is not high enough to estimate AOA,it can be taken into altitude tracking error calculation.The nominal command of virtual control variable ¯x2is designed as
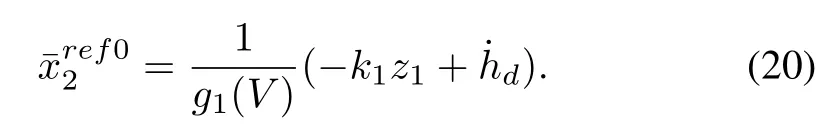
To avoid the explosion of complexity in calculating the derivative,a fi rst-order fi lter is introduced to obtain the differentiation of the virtual control input,i.e.,
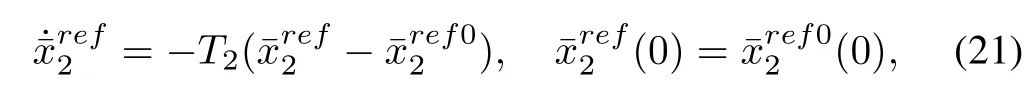
whereT2is the time constant of fi lter and should be as large as possible to promise the fast tracking.
Step 2.De fi ne the dynamic surface equation in Eq.asz2:= sinwhose dynamics can be calculated by(6),i.e.,

wherex3is the virtual control input of this step,the nominal value ofis chosen to satisfy the following equation:

Let the nominal virtual control variable value passing through the following fi rst-order fi lter:

whereT3is the time constant of fi lter.
Step 3.De fi ne dynamic surface asz3:=x3,its dynamics can be calculated from(6),i.e.,

wherex4is the virtual control variable of this step,and its nominal value is selected as

This nominal virtual control variable value will also pass through the following fi rst-order fi lter to get the derivative of the virtual control variable:

whereT4is the fi lter time constant.
Step 4.De fi ne dynamic surface asz4:=x4.From (8),the dynamics ofz4is calculated as

Select the control input to satisfy

C.Controller Design for Velocity Loop
The controller for velocity loop adopts dynamic inversion method.De fi ning tracking error aszV=V-Vd,then we can deduce the derivative ofzVas
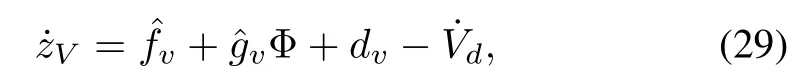
wheredvdenotes the uncertainties of velocity loop,which is induced by observer error ofα.It can be estimated from the following extended state observer[26-27]:
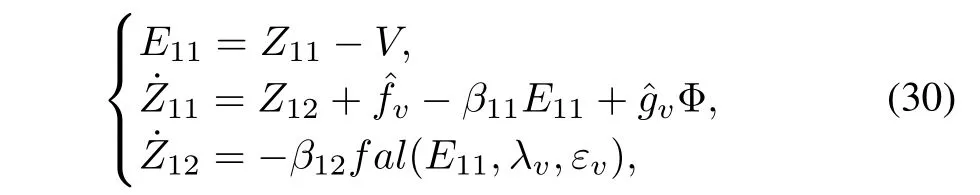
where 0<λv<1,εv>0,β11>0,β12>0 are design coef fi cients,and the functionfalis de fi ned as

Then the controller can be designed as
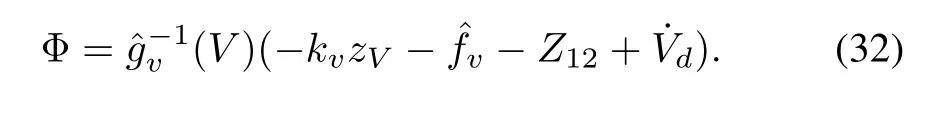
D.Stability and Performance Analysis
In this section,we will prove that by using the proposed output feedback dynamic surface control scheme,the semiglobal stability of the closed-loop system can be guaranteed.Furthermore,the tracking performance can be achieved through tuning control coef fi cients under an initialization error constraint condition.
De fi ne the error between the nominal and actual values of virtual control variable as wherekpis a constant satisfyingkp=e-(kp+1).

We conclude the stability of the closed-loop altitude subsystem in the following theorem.
Theorem 1.Given motion equations(6)~(8)for the altitude loop of hypersonic fl ight vehicle,the proposed dynamic surface controller(28),together with the FLSs estimator(16), there exist proper positive numberski,Tj(i=1,2,3,4,j=2,3,4)and a negative numberM,such that all signals of the closed-loop altitude system are uniformly bounded,and the altitude tracking errorz1converges to a residual set that can be made arbitrarily small by properly choosing some design parameters.
Proof.De fi ne the Lyapunov function candidate as
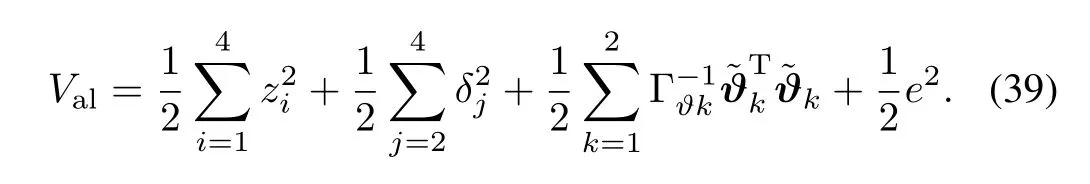
Along the trajectories(29)-(32),the derivative of the Lyapunov function candidate can be calculated as
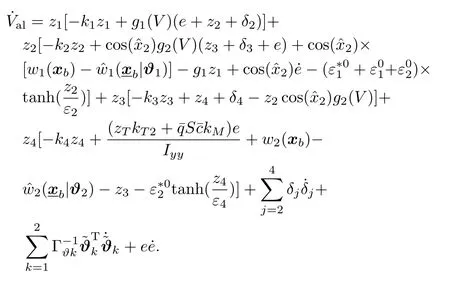
By simplifying the equation,the derivative of Lyapunov function is transformed into

According to(37),it can be deduced that


wherepis a suitable positive number.Note thatAandBare compact sets on R3and R7,which makesA×Ba compact set on R10,the continuous functionsψjin(33)forj=2,3,4, have maximums onA×B,i.e.,Mψj.Moreover,by using Young inequality,we have

whereςMis an arbitrary constant.In view of(44),(43)can be rewritten as

Let the control gain, fi lter gain and observer gain satisfy the following inequalities:

Then,(45)can be transformed to

The extended state observer can estimate the disturbancedvin fi nite time,and the estimation error=dv-Z12can be extremely small[26-27],so the tracking error dynamics can be approximated by=-kvzV,which guarantees the stability of velocity loop and convergence of velocity tracking error.
The generalized elastic coordinate system can be treated as a disturbance to the rigid-body system[29].Theorem 1 shows that the closed-loop altitude system has strong disturbance attenuation ability.Velocity loop also possesses high disturbance attenuation ability with the help of extended state observer. Thus,the boundedness of generalized elastic coordinate can guarantee the stability of rigid system.With Assumption 1,the dynamics of generalized elastic coordinate is mainly affected by AOA,so the boundedness of AOA can guarantee the stability of the structure elastic system from the system dynamics in(1).Thus,the stability of the whole system can be guaranteed by the small-gain theorem[30].
IV.SIMULATIONS
To show the performance of the controllers proposed in previous sections,simulations have been performed on the fully nonlinear vehicle model described by(1).The vehicle is desired to track the velocity and altitude references initialized atV0=2347.6m·s-1,h0=25908m,γ0=0 deg.The reference commands of velocity and altitude are generated by f i ltering step reference commands using two second-order pref i lters with natural frequencyωf=0.03rad/s and damping factorξf=0.95.Referencehd(t)is generated to let the vehicle climb 6.1km in about 180s in two steps,whereas the velocity reference is one step signal with the increase of 228.6m/s.
The simulations are accomplished in three steps,corresponding to the nominal model,uncertain model with compensation,and the comparisons with other schemes.The compensation-control involves fuzzy logic compensation and uncertainty estimation error compensation.
The parameters used in the controllers of all simulations are shown in Table III.The fi rst simulation is only for the nominal model,indicating the uncertainties are ignored,that is to say,w1=w2=0.The reference signals of virtual control variables are chosen according to equations(20),(23)and(25), and the control input is computed from(28).In this study, the constraints on states and inputs are dealt with indirectly by tuning the controller gains,including the parameters of the pre- fi lter and dynamic surface gainki(i=1,···,4). The selection of gainkishould make the inner loop respond quicker than the outer loop.The controller gains used in all simulations are shown in Table III.

TABLE III CONTROLLER PARAMETERS
Figs.3 and 4 con fi rm that the controllers provide stable tracking of the reference trajectories of altitude and velocity and exact convergence to the reference command.The fl ightpath angle reference command,as depicted in Fig.5 is well tracked.The fl ight-path angle is smaller than 1.5deg during the whole process,which validates the small angle assumption used in Section II.

Fig.3.The tracking curve of altitude command.
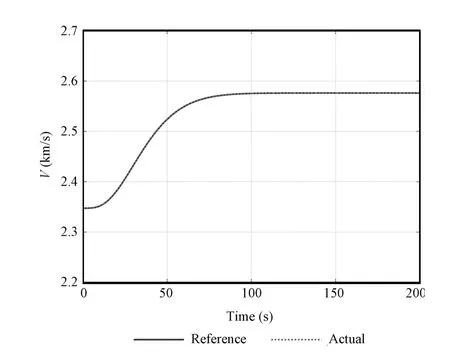
Fig.4.The tracking curve of velocity command.

Fig.5.The tracking curve of FPA.
Figs.6 and 7 show the tracking performance of the virtual control variables of pitch angle and its rate.The virtual controlcommands are smooth within their bounds,and are nicely tracked.The estimation curve of AOA is given in Fig.9,which shows the good performance of the proposed estimator.

Fig.6.The tracking curve of pitch angle.
According to the simulation results in nominal condition, it is clear that even though the exact information on AOA is immeasurable,the proposed adaptive fuzzy output feedback controller guarantees both the stability and good tracking performance of the closed-loop system.

Fig.7.The tracking curve of pitch angle rate.
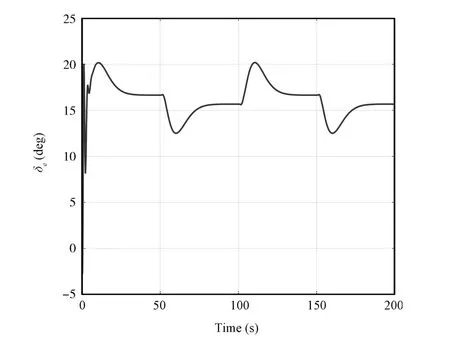
Fig.8.The curve of elevator de fl ection.
The second simulation is performed for the system with uncertainties.The references of velocity,altitude,and fl ightpath angle are the same as those in the fi rst simulation.It is assumed that the true value of some aerodynamic parameters includingare unknown and different from the nominal value within the tolerance of 5%.Additionally,the mass and moment of inertia vary by 10%of their nominal values.The simulation is conducted considering the effects of the generalized elastic coordinates.

Fig.9.The estimate in curve of AOA.
The fuzzy weighting values are computed with update laws (39)and(40).The gains of the update laws are selected asTϑ1=80,β1=0.05,Tϑ2=140,β2=0.05.Gaussian membership function is used,and the variances should be in the suitable range,corresponding to the partitioning points selected.From Remark 1,the uncertainty from the difference betweenαrefandαcan also be seen as coef fi cient uncertainty, sow1andw2can be predigested as the functions ofα,δeandη.In the FLSs,we useˆα,δeandη∗as inputs.The partitioning points are chosen as-4,-1,2,5,8deg,and-20,-15,-10,-5,0,5,10,15,20deg forˆαandδe,respectively.The partitioning points forηare selected according to the scale of each generalized elastic coordinate which can be estimated by the trim value.In this simulation,we select-1.5 to 1.5 with the interval of 0.3 forη1,-0.6 to 0.6 with the interval of 0.06 forη2and-0.12 to 0.12 with the interval of 0.03 forη3.The fuzzy membership functions forˆαare given as follows,and the fuzzy membership functions forδeandηare similar toˆα:

It can be seen that the tracking error of altitude remains very well behaved in the presence of model uncertainties. The tracking errors remain remarkably small during the entire maneuver,and vanish asymptotically.The good performance of the fuzzy compensators are demonstrated.In fact,extensive studies are performed on changing the fuzzy membership functions and weighing update gains for exact estimation of model uncertainties.
The effect ofδeon the generalized elastic coordinate is also analyzed in this simulation.It can be seen from Fig.15 thatthe effect ofδeis much smaller than that of other parts,mainly the angle of attack.

Fig.10.The tracking curve of altitude command with uncertainty.
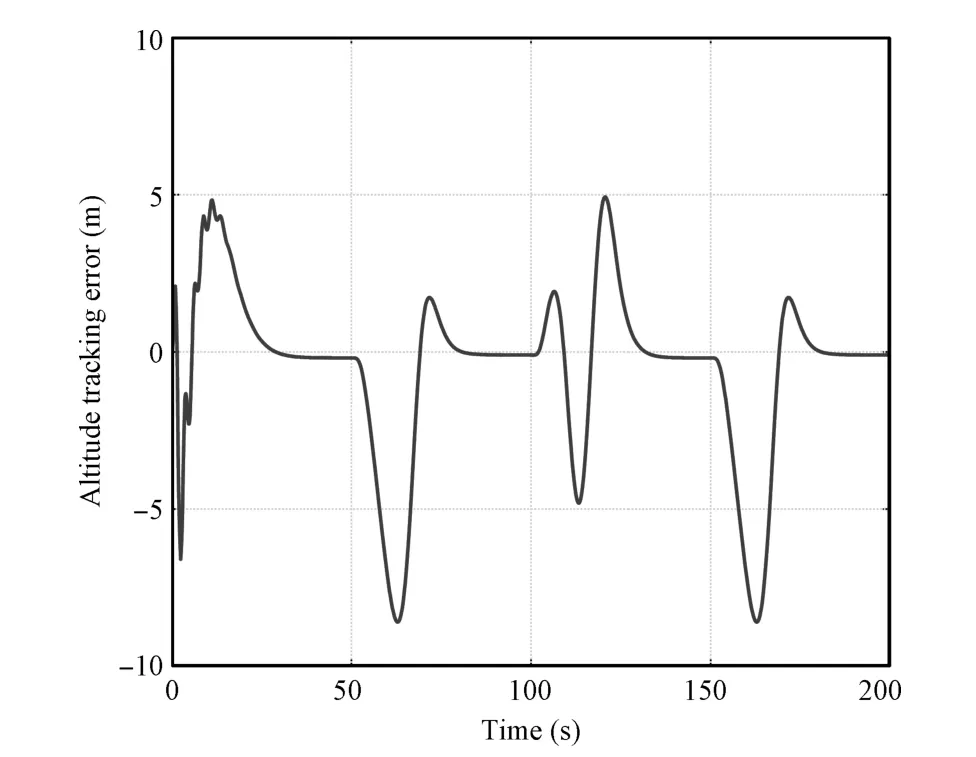
Fig.11.The tracking error of altitude.

Fig.12.The tracking curve of altitude command with uncertainty.
Reference[13]proposes a kind of sliding mode observer to estimate FPA and AOA.The observer and controller are designed separately.In this paper,we will give the off-line estimation results of SMO,and make a comparison with our proposed observer.The design parameters of SMO are selected according to the principle given in[13].The simulation is conducted in the same uncertainty condition as in the second simulation.
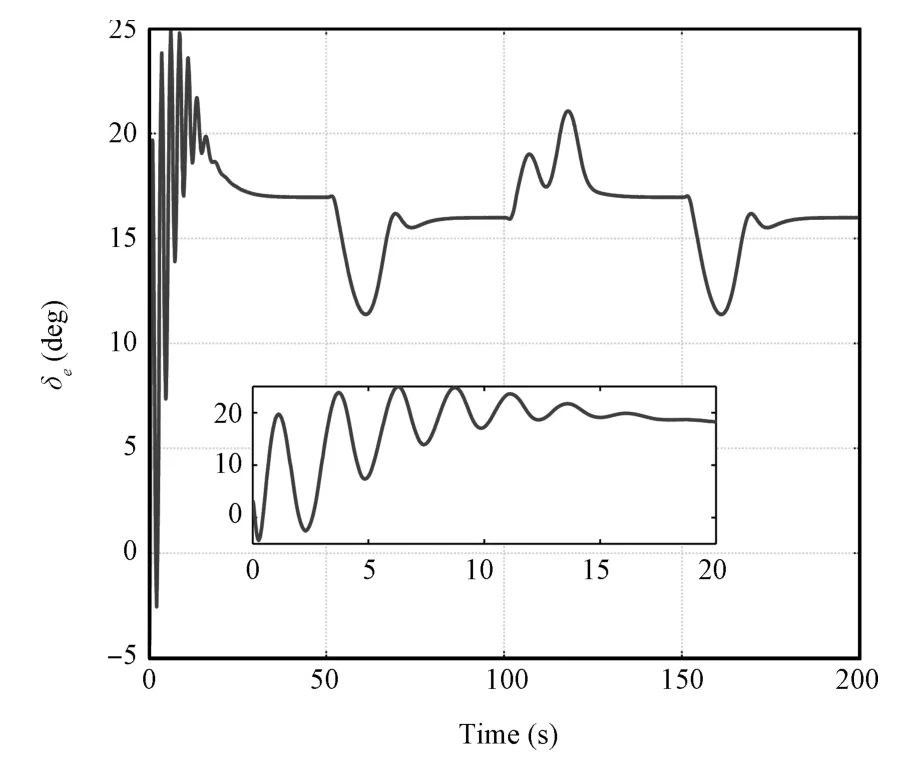
Fig.13.The tracking error of altitude.
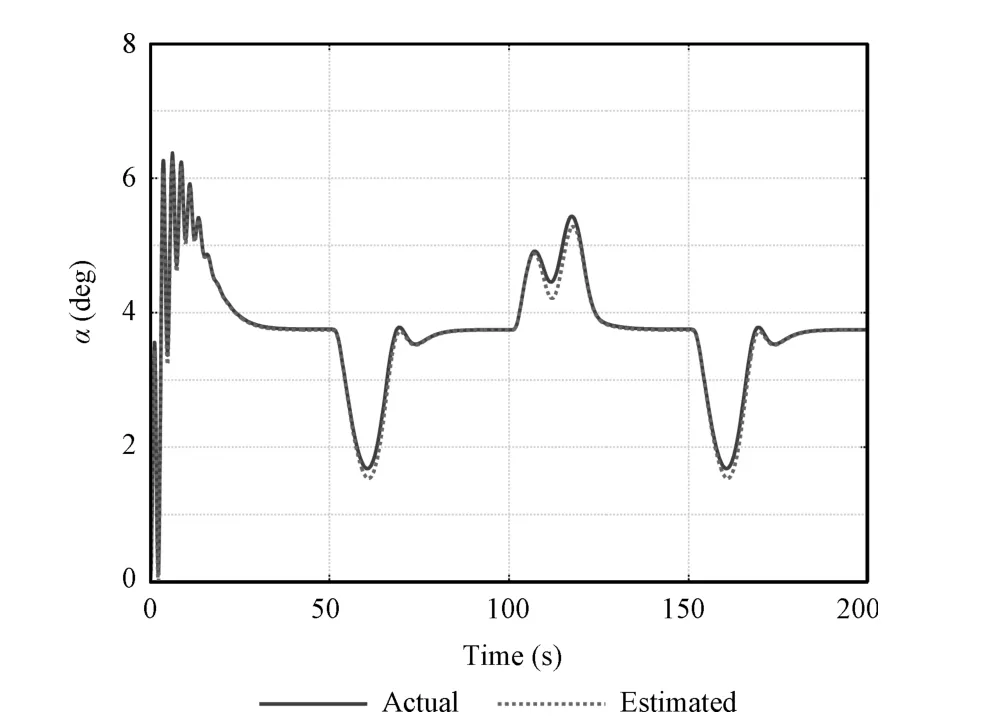
Fig.14.The estimation curve of AOA.

Fig.15.The curve of elevator de fl ection.
The simulation results are given in Figs.16~19.From Fig.17,it can be seen that the estimation error of pitch rate converges to zero quickly,but this do not ensure the convergence of AOA estimation error,which can be seen from Fig.19.The existence of uncertainty changes the origin of the observer,which make estimation value of AOA cannot converge to its true value.The estimation error of AOA affects the convergence of altitude and FPA,which can be seen from Figs.16 and 18.In the proposed method of this paper,the observer and controller are designed in associated manner. The uncertainty is estimated by FLSs whose parameters are adaptively tuned in the controller.Thus,the uncertainty is well compensated in the estimator.Besides,the stability analysis of observer can be proved in theory.

Fig.16.Altitude estimation error with SMO.
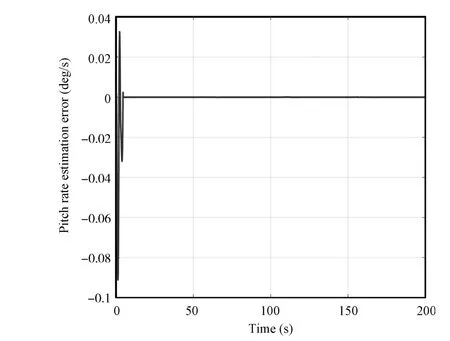
Fig.17.Pitch estimation error with SMO.
Remark 4.Comparing to state feedback based backstepping control scheme[16-17]for the hypersonic vehicle,the proposed scheme in this paper is constructed using limited state information,but achieves relatively good tracking performance of velocity and altitude.Additionally,dynamic surface technique used in this paper avoids the complexity explosion of backstepping control.
V.CONCLUSION
The usual air-data measurement system cannot work well due to hypersonic aerodynamic heating.Thus,output feedback controller is an essential issue for generic airbreathing hypersonic fl ight vehicle.A novel output feedback control scheme is developed in this paper.Estimated AOA value is acquired through a reduced order observer only using pitch angle and its rate information.The control system is constructed based on the AOA signal from observer.Dynamic surface technique is used in controller design for avoiding complexity explosion of traditional backstepping control.Fuzzy logic based compensator is used in the controller to dispose the inaccuracy and uncertainty of the model.Different from the existing output feedback controller in the literature,this scheme not only uses limited information,but also takes model uncertainty into consideration,which greatly strengthen the robustness of control system.At last,simulation results demonstrate the good performance of the proposed method.
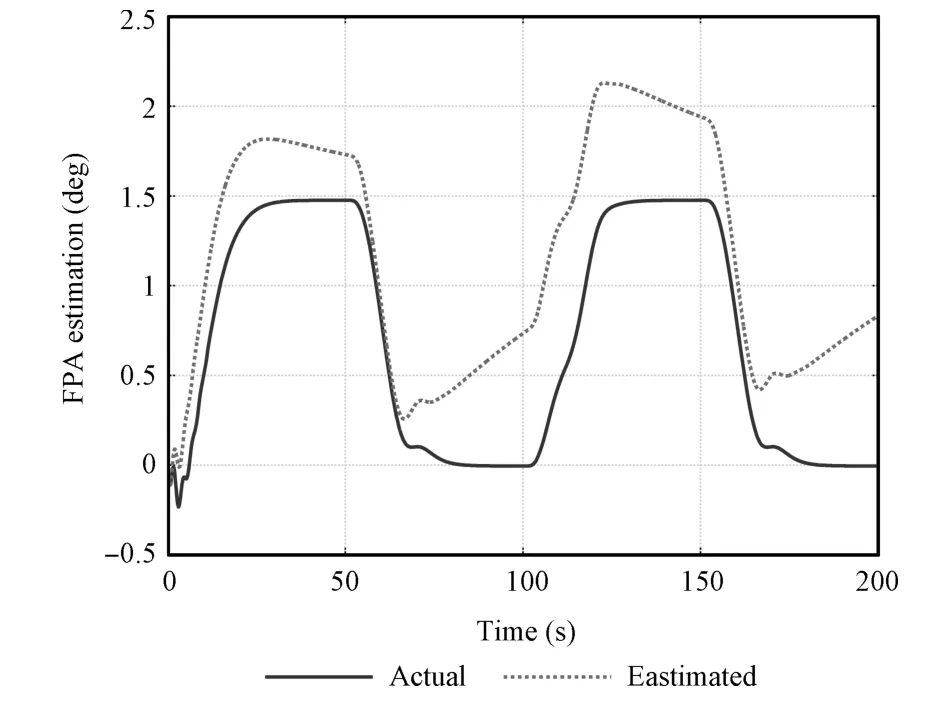
Fig.18.FPA estimation curve with SMO.
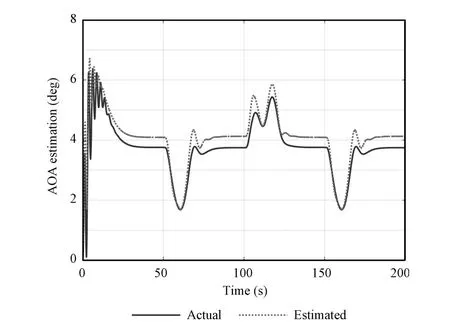
Fig.19.AOA estimation curve with SMO.
REFERENCES
[1]Chavez F R,Schmidt D K.Uncertainty modeling for multivariablecontrol robustness analysis of elastic high-speed vehicles.Journal of Guidance,Control,and Dynamics,1999,22(1):87-95
[2]Zong Q,Ji Y H,Zeng F L,Liu H L.Output feedback backstepping control for a generic hypersonic vehicle via small gain theorem.Aerospace Science and Technology,2012,23(1):409-417
[3]Bolender M A,Doman D B.Nonlinear longitudinal dynamical model of an air-breathing hypersonic vehicle.Journal of Spacecraft and Rockets, 2007,44(2):374-387
[4]Sun Chang-Yin,Mu Chao-Xu,Yu Yao.Some control problems for near space hypersonic vehicles.Acta Automatica Sinica,2013,39(11): 1901-1913(in Chinese)
[5]Bao Wei-Min.Present situation and development tendency of aerospace control techniques.Acta Automatica Sinica,2013,39(6):609-702(in Chinese)
[6]Dickeson J J,Rodriguez A A,Sridharam S,Benavides J,Soloway D. Decentralized control of an air-breathing scramjet-powered hypersonic vehicle.In:Proceedings of the 2009 AIAA Guidance,Navigation and Control Conference.Chicago,IL:AIAA,2009.AIAA-2009-6281
[7]Groves K P,Sigthorsson D O,Serrani A,Yurkovich S,Bolender M A,Doman D B.Reference command tracking for a linearized model of an air-breathing hypersonic vehicle.In:Proceedings of the 2005 AIAA Guidance,Navigation,and Control Conference.San Francisco, CA:AIAA,2005.AIAA-2005-6144
[8]Lind R,Buf fi ngton J,Sparks A.Multi-loop aeroservoelastic control of a hypersonic vehicle.In:Proceedings of the 1999 AIAA Guidance, Navigation,and Control Conference.Portland,OR:AIAA,1999.AIAA-99-4123
[9]Rick L.Linear parameter-varying modeling and control of structural dynamics with aerothermoelastic effects.Journal of Guidance,Control, and Dynamics,2002,25(4):733-739
[10]Wilcox Z D,Mackunis W,Bhat S,Lind R,Dixon W E.Lyapunov-based exponential tracking control of a hypersonic aircraft with aerothermoelastic effects.Journal of Guidance,Control,and Dynamics,2010,33(4): 1213-1224
[11]Hu X,Wu L,Hu C,Gao H.Fuzzy guaranteed cost tracking control for a fl exible air-breathing hypersonic vehicle.IET Control Theory and Applications,2012,69(4):1238-1249
[12]Wang Q,Stengel R F.Robust nonlinear control of a hypersonic aircraft.Journal of Guidance,Control,and Dynamics,2000,23(4):577-585
[13]Xu H J,Mirmirani M D,Ioannou P A.Adaptive sliding mode control design for a hypersonic.Journal of Guidance,Control,and Dynamics, 2004,27(5):829-838
[14]Hu X X,Wu L G,Hu C H,Gao H J.Adaptive sliding mode tracking control for a fl exible air-breathing hypersonic vehicle.Journal of the Franklin Institute,2012,349(2):559-577
[15]Gao G,Wang J Z.Reference command tracking control for an airbreathing hypersonic vehicle with parametric uncertainties.Journal of The Franklin Institute,2013,350(5):1155-1188
[16]Fiorentini L,Serrani A,Bolender M,Doman D B.Nonlinear robust adaptive control of fl exible air-breathing hypersonic vehicles.Journal of Guidance,Control,and Dynamics,2009,32(2):401-416
[17]Bialy B J,Klotz J,Curtis J W,Dixon W E.An adaptive backstepping controller for a hypersonic air-breathing missile.In:Proceedings of the 2012 AIAA Guidance,Navigation and Control Conference.Minneapolis,MN:AIAA,2012.AIAA-2012-4468
[18]David O S,Pete J,Andrea S.Robust linear output feedback control of an airbreathing hypersonic vehicle.Journal of Guidance,Control,and Dynamics,2008,31(4):1052-1066
[19]Zhang X,Lin Y.Adaptive output feedback tracking for a class of nonlinear systems.Automatica,2012,48(9):2372-2376
[20]Fan H J,Han L X.,Wen C Y,Xu L.Decentralized adaptive outputfeedback controller design for stochastic nonlinear interconnected systems.Automatica,2012,48(11):2866-2873
[21]Jiang Zhong-Ping,Huang Jie.Stabilization and output regulation by nonlinear feedback:a brief overview.Acta Automatica Sinica,2013, 39(9):1389-1401(in Chinese)
[22]Tong S C,Li Y M,Feng G,Li T S.Observer-based adaptive fuzzy backstepping dynamic surface control for a class of MIMO nonlinear systems.IEEE Transactions on Systems,Man,and Cybernetics-Part B: Cybernetics,2011,41(12):1124-1135
[23]Parker J T,Serrani A,Yurkovich S,Bolender M A,Doman D B.Controloriented modeling of an air-breathing hypersonic vehicle.Journal of Guidance,Control,and Dynamics,2007,30(3):856-869
[24]Fiorentini L.Nonlinear Adaptive Controller Design for Air-Breathing Hypersonic Vehicles[Ph.D.dissertation],The Ohio State University, USA,2010.
[25]Tong S C,Li Y M,Feng G,Li T S.Observer-based adaptive fuzzy backstepping dynamic surface control for a class of non-linear systems with unknown time delays.IET Control Theory and Applications,2011, 12(5):1426-1438
[26]Han J Q.From PID to active disturbance rejection control.IEEE Transactions on Industrial Electronics,2009,56(3):900-906
[27]Xia Y Q,Zhu Z,Fu M Y,Wang S.Attitude tracking of rigid spacecraft with bounded disturbances.IEEE Transactions on Industrial Electronics, 2011,58(2):647-659
[28]Chen M,Ge S S,Ren B B.Adaptive tracking control of uncertain MIMO nonlinear systems with input constraints.Automatica,2011, 47(3):452-465
[29]Sun H F,Yang Z L,Zeng J P.New tracking-control strategy for airbreathing hypersonic vehicles.Journal of Guidance,Control,and Dynamics,2013,36(3):846-859
[30]Jiang Z P,Teel A R,Praly L.Small-gain theorem for ISS systems and application.Mathematics of Control,Signals,and Systems,1994,7(2): 95-120


Qing Wang received her bachelor,master and Ph.D. degrees from Northwestern Polytechnical University in 1990,1993 and 1996,respectively.She is currently a professor at the School of Automation Science and Electrical Engineering,Beihang University. Her research interest covers guidance and control of aerospace fl ight vehicles,fault diagnosis and tolerant control,switched control and its application on fl ight control system.

Chaoyang Dong received his bachelor degree from Beihang University in 1989,master degree in fl ight dynamics from Northwestern Polytechnical University in 1992,and Ph.D.degree in guidance,navigation and control from Beihang University in 2007. He is currently a professor of at the School of Aeronautic Science and Engineering,Beihang University.His research interest covers vehicle modeling and control,simulation of aerospace vehicles and synthesis of aerospace electrical system.
u
his bachelor degree in fl ight vehicle design and engineering from Northwestern Polytechnical University in 2009.He is currently a Ph.D.candidate at the School of Automation Science and Electrical Engineering,Beihang University. His research interest covers nonlinear control theory and its application on fl ight vehicle.Corresponding of this paper.
Manuscript received October 10,2013;accepted April 15,2014.This work was supported by Natural National Science Foundation of China(61273083, 61374012).Recommended by Associate Editor Changyin Sun.
:Delong Hou,Qing Wang,Chaoyang Dong.Output feedback dynamic surface controller design for airbreathing hypersonic fl ight vehicle.IEEE/CAA Journal of Automatica Sinica,2015,2(2):186-197
Delong Hou is with the School of Automation Science and Electrical Engineering,Beihang University,Beijing 100191,China,and also with Beijing Institute of Electronic System Engineering,Beijing 100854,China (e-mail:dlh8855@163.com).
Qing Wang and Chaoyang Dong are with the School of Automation Science and Electrical Engineering,Beihang University,Beijing 100191,China(email:wangqing@buaa.edu.cn;dongchaoyang@buaa.edu.cn).
杂志排行
IEEE/CAA Journal of Automatica Sinica的其它文章
- Single Image Fog Removal Based on Local Extrema
- An Overview of Research in Distributed Attitude Coordination Control
- Operation Ef fi ciency Optimisation Modelling and Application of Model Predictive Control
- Cloud Control Systems
- Stable Estimation of Horizontal Velocity for Planetary Lander with Motion Constraints
- Production Line Capacity Planning Concerning Uncertain Demands for a Class of Manufacturing Systems with Multiple Products
