Operation Ef fi ciency Optimisation Modelling and Application of Model Predictive Control

Xiaohua Xia and Jiangfeng Zhang

Operation Ef fi ciency Optimisation Modelling and Application of Model Predictive Control

Xiaohua Xia and Jiangfeng Zhang

—The ef fi ciency of any energy system can be charaterised by the relevant ef fi ciency components in terms of performance,operation,equipment and technology(POET).The overall energy ef fi ciency of the system can be optimised by studying the POET energy ef fi ciency components.For an existing energy system,the improvement of operation ef fi ciency will usually be a quick win for energy ef fi ciency.Therefore,operation ef fi ciency improvement will be the main purpose of this paper.General procedures to establish operation ef fi ciency optimisation models are presented.Model predictive control,a popular technique in modern control theory,is applied to solve the obtained energy models.From the case studies in water pumping systems,model predictive control will have a prosperous application in more energy ef fi ciency problems.

Index Terms—Model predictive control(MPC),operation ef ficiency,energy ef fi ciency.

I.INTRODUCTION

W ITH the increasing shortage of energy supply,energy ef fi ciency improvement has been widely recognised as the quickest and most effective method to alleviate energy supply pressure.Energy ef fi ciency generally consists of many components,such as management ef fi ciency,operational ef fi ciency,carrier ef fi ciency,information and control ef fi ciency,billing ef fi ciency,maintenance ef fi ciency,conversion ef fi ciency,thermal ef fi ciency,luminous ef fi ciency,etc.In [1-3],these energy ef fi ciency components were summarised and classi fi ed as performance ef fi ciency,operation ef fi ciency, equipment ef fi ciency,and technology ef fi ciency(POET).A prominent application of this kind of POET classi fi cation is to prevent the loss of energy ef fi ciency improvement opportunities,which is shown in the energy audit practices[4].This POET classi fi cation can also be applied to general energy optimisation so that all the key aspects of energy ef fi ciency are optimised.Note the fact that proper sizing and matching of different system components,which include changing the operational schedules amongst others,for a given energy system will often save both energy and energy cost in manyscenarios,therefore this paper focuses on the operation ef ficiency optimisation.Operation ef fi ciency is often evaluated in terms of performance indicators such as energy,power, cost,etc.[1].It follows that operation ef fi ciency can usually be written as an optimisation problem with objective functions to be the minimisation of energy or power consumption,energy cost,etc.This kind of optimisation problem is formulated over a given time period,and can often be understood as an optimal control problem since the time dependent operation functions can be treated as the control input in optimal control.Thus various control techniques will be applicable to these energy problems.This paper focuses on the establishment of operation ef fi ciency optimisation models and the application of model predictive control(MPC)to solve the obtained models.

MPC is well-known for its ability to use simple models,to handle constraints,and also for its closed-loop stability and inherent robustness.Therefore,MPC has become a popular tool for many industrial problems[5-7].The MPC technique can be applied to many operation ef fi ciency optimisation problems in which the energy systems are operated over evolving time spans.In the literature,there are various case studies on operation ef fi ciency optimisation,and these studies include cases such as steel plant peak load management[8], energy management of a petrochemical plant[9],rock winder systems[10],water pumping systems[11-12],power generation economic dispatch[13],power generation maintenance[14],etc. From these studies,it turns out that the most challenging part in the MPC applications is not the MPC itself,but the energy system modelling.Also existing studies focus on particular systems only,a general description on the operation ef fi ciency optimisation modelling techniques is necessary.This paper summarises these modelling techniques and particularly formulates the general logic correlation constraints.These general modelling principles are illustrated by a few examples which include mineral processing,pumping systems and plant maintenance.

The paper is organized as follows.The next section provides a uni fi ed modelling framework for operation ef fi ciency optimisation.General steps to apply MPC principles are also summarised.Section III provides some case studies,and the last section is the conclusion.

II.OPERATION EFFICIENCY OPTIMISATION MODELLING ANDMPCAPPLICATIONS

According to[1],operation ef fi ciency is a system wide measure which is evaluated by considering the proper coordination of different system components.This coordination of system components consists of the physical,time,and human coordi-nation parts.Operation ef fi ciency has the following indicators: physical coordination indicators(sizing and matching);time coordination indicator(time control);and human coordination indicator.It is usually dif fi cult to model the human coordinations in operation ef fi ciency,therefore we will focus on the physical and time coordination indicators.

A.Optimal Control Modelling for Operation Ef fi ciency

The purpose to optimise operation ef fi ciency is usually to save energy and energy cost while at the same time to

meet certain service requirement.In the following,the objective functions of the operation ef fi ciency operation model will be chosen as both the energy and energy cost.

Assume that an energy system consists ofNcomponents, each of them can be independently controlled as on or off. Whenever thei-th component is switched on,its power consumption will be its rated powerPikW fori=1,2,···,N1, and be any value between 0 and its rated powerPikW fori=N1+1,N2+2,···,N,whereN1≤N.The fi rstN1components have only simple on/off status and include examples such as electric water heaters,electric kettles,and incandescent lights,while the lastN-N1components have variant powers and examples can be motors controlled by variable speed drives.Let the energy price at timetbe$p(t)/ kWh;then the energy consumption functionfEand energy cost functionfCover a fi xed time interval[t0,tf]are given below.

whereui(t)represents the on/off status variable and is de fi ned as follows:

The two functionsfEandfCwill be minimised.After formulating these two objective functions,the remaining part on the modelling is to fi nd proper constraints.The coordination within theNcomponents of the system can be very complicated.For illustration purposes,the following typical types of coordination relations between theseNcomponents are modelled.

1)Logic correlations

a)The statusui(ta)does not affect the status ofuj(tb).For this case,we do not need to build any mathematical constraint.

b)Ifui(ta)is in the switched on status,thenuj(tb)must be in the off status.To fi nd out a mathematical equivalent expression for this constraint,the following sign function is introduced.Let sgn(x)be 1 ifx＞0;0 ifx=0;and-1 ifx＜0.Noting the fact thatui(ta)anduj(tb)are nonnegative, then it follows that this constraint is equivalent to:

A prominent bene fi t to use sign function to obtain the above constraint is that this type of constraint covers the case wheniorjis greater thanN1,that is,it covers the case where those components with variable powers are involved.An example for this type requirement can be that a piece of equipment is powered either by the grid,or by a distributed generation system,but cannot be by the two at the same time.Then the connection status of the main grid to the equipment at timetcorresponds tou1(t),while the connecting status of the distributed generation system corresponds at timettou2(t). This constraint following two constraints are derived as:

c)Ifui(ta)is in the switched on status,thenuj(tb)must be in the on status.This constraint is equivalent to the following inequality.

An example for this case is that at a residential home,when people switched on the TV at the lounge in the evening,they must have switched on the light in the lounge fi rst.That is, when the status of the TV at timetais on,then the status of the light must already be on atta.

d)Ifui(ta)is in the switched off status,thenuj(tb)must be in the on status.This constraint is equivalent to:

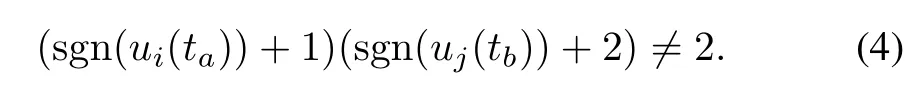
e)Ifui(ta)is in the switched off status,thenuj(tb)must be in the off status.This constraint is equivalent to:

2)Mass balance

Mass balance is a very common constraint in various energy systems.It can often be simpli fi ed as that at a given time period,the mass should be balanced at any system component. Mass balance equation can also be established for the overall system.For illustration purpose,we establish only the mass balance equation for a single system component:

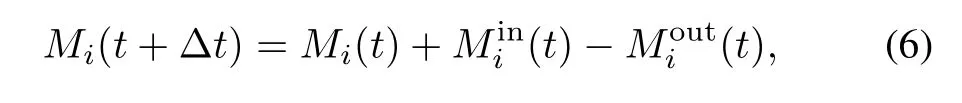
whereMi(t)andMi(t+Δt)are the masses of thei-th component at timetandt+Δt,respectively;while(oris the amount of mass entered into(or left) componentiduring the time period(t,t+Δt).The massMi(t0)at the initial timet0is often given.Theandare often determined by the on/off status of the (i-1)-th andi-th components,respectively.That is,there are functionshiandgisuch that=hi-1(ui-1(t)) and=gi(ui(t)).In many applications,thesehiandgiare often linear functions,and thus

whereai-1andbiare constants.If there is no mass losses between the(i-1)-th component and thei-th component and ignore the time taken for the mass to fl ow from component (i-1)into componenti,thenIn a water pumping system,this mass balance equation is that the watervolume changes in a reservoir equals the difference of the amount of water entering into the reservoir and the amount of water leaving the reservoir.In conveyor belt systems,the mass balance equation represents the mass changes at a stock silo equals the differences between incoming and outgoing masses to and from the stock silo.

3)Energy balance

Energy balance can be established similarly as the mass balance equation(6)either at a system component level or the overall system level.That is,the two types of energy balance equations can be brie fl y written as the following.

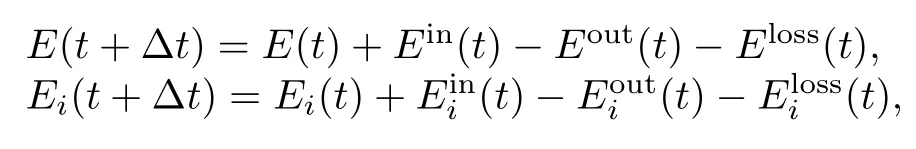
whereErefers to energy(e.g.,kinetic energy,potential energy),E(t)orEi(t)represent the energy stored in the whole system or componentiat timet,the superscripts in,out,loss represent the energy fl ows into,useful energy fl ows out from, or energy losses at the whole system or system component during the time period(t,t+Δt).is usually a function of the switching statusui(t)and/or,i.e.,there exists a functionαisuch that(t)is often a function determined by the switching statusui(t)and/or a given external demandDi(t),that is,there exists a functionβsuch that=βi(ui(t),Di(t)). The energy lossis often determined by external variables such as temperature differences,humidity,pressure, material thermal convection coef fi cients,etc.,and it is usually computable ifui(t)is given.Therefore,there exists a functionγisuch that=γi(ui(t)).Similarly,one can calculateEin(t),Eout(t)andEloss(t).

4)Process and service correlations

To meet special process or service requirements,some system components are often requested to be switched on simultaneously for a minimum time duration within a given period.This requirement is equivalent to request each of these components to be switched on for a minimum time duration at the given period.Assume that thei-th component must be switched for at least a duration of ΔTwithin the period [t1,t2].This requirement can be formulated as the following inequality:R(ui(t))dt≥ΔTThere are also other types of process and service correlations,such as the delivered electrical power from a generator must meet the end user demand,an air conditioner must deliver the expected cooling load,and the pressure of compressed air must satisfy speci fi ed ranges.The corresponding constraints need to be worked out according to speci fi c requirements.

5)Boundary constraints

There are often boundary constraints for some intermediate variables.For example,if the purpose is to save at least 10000kWh per year,and to save energy cost at least $10000/year,then the two constraints can be written asfE≥10000 andfC≥10000.Other examples include the storage capacity limit of mineral silos in a conveyor belt system,reservoir capacity limit in a pumping systems, generator minimum and maximum power output,minimum and maximum temperature limits of hot water inside a water heater,steam pressure limit of a boiler,etc.These intermediate variables can usually be written as a function of the switching statusui(t),i=1,···,N,according to relevant physical dynamic processes.Generally,the following inequality is obtained:

The above mathematical constraints provide a summary for those frequently met physical requirements in many energy systems.However,due to the complex nature of physical processes and service requirements,there will be much involved cases where none of the above derived models is directly applicable,and further analysis on the corresponding energy systems must be done.

B.MPC for Optimal Control Models

The model obtained in(1)～(8)is an optimal control model with control variablesu1(t),···,uN(t).This optimal control problem is often dif fi cult to solve since the sign function is discontinuous and the variablesu1(t),···,uN1(t)are binary integers.Therefore,this problem is discretised using the sampling oft0＜t1＜···＜tm=tf,Δt=(tm-t1)/m=ti+1-ti, 1≤i≤m,and then reformulated as follows:

whereU=(u1(t1),u2(t1),···,uN(t1),u1(t2),u2(t2),···,uN(t2),u1(tm),···,uN(tm))Tis the control variable.This discrete form is easy to be implemented in MPC approach.In the MPC approach,the optimisation horizon is movable over any consecutive time lengthmΔt=tm-t0, i.e.,it is solved over[tk,tm+k]for allk=0,1,2,···,for the corresponding optimisation problem:

withthevariableUk=(u1(tk+1),u2(tk+1),···,uN(tk+1),u1(tk+2),u2(tk+2),···,uN(tk+2),u1(tk+m),···,uN(tk+m))T.After obtaining the solution,u1(tk+1),u2(tk+1),···,uN(tk+1)are implemented over the time period [tk+1,tk+2).At the end of the time interval[tk+1,tk+2), initial values are updated according to real time changes,and the above problem(10)is resolved over the time interval [tk+1,tk+m+1]for the variableUk+1which is de fi ned in the same way;see[16]for a similar MPC algorithm.The above MPC iteration steps will be applied in the case studies in Section III.

III.CASE STUDIES

In this section,a mineral processing system is investigated to illustrate the energy modelling procedures in Section II-A. The water puri fi cation system in[11]is restudied to propose an alternative model.The general plant maintenance problem is formulated to generalise the special case of generator maintenance in[14].

Fig.1.Mineral processing system.

A.Mineral Processing System

In the mineral processing system in Fig.1,minerals are fed at the rate ofF(t)tons/hour to the 80kW conveyor belt B1.From the 200kW crusher C1,these minerals are further transported by conveyor belt B2 to a 50kW screen system. After the screen,smaller size minerals go to the 150kW conveyor belt B3,larger size ones go to the 100kW crusher C2 to be recrushed and then sent back to conveyor belt B2. Minerals from B3 are sent to a 3000 ton stock silo,where they will be further supplied to the 50kW conveyor belt B4 and from B4 to the 150kW conveyor belt B5.The plant feed demand at the end of conveyor belt B5 isD(t)tons/hour.The question for this problem is to minimise electricity cost in terms of a time-of-use electricity tariff over the time interval [t0,tN].Discretise[t0,tN]ast0＜t1＜···＜tN,t1-t0=t2-t1=···=tN-tN-1=ΔT.

The overall mineral processing energy system consists of conveyors B1,B2,B3,B4,B5;crushers C1,C2;and a screen. De fi ne the on/off switching status functions for these system components as follows.represents the on/off status of thei-th conveyor Biat thek-th time interval,withi=1,2,3,4,5;andare the on/off status of crushers C1 and C2 at thek-th time interval,respectively;andis the on/off status of the screen at timek.The values of these switching status functions can only be 0 or 1,representing“off”or“on”status. Following the steps in Section II-A,the objective function to minimise electricity cost over[t0,tN]for a given electricity tariff$pk/kWh,k=1,···,N,is written as

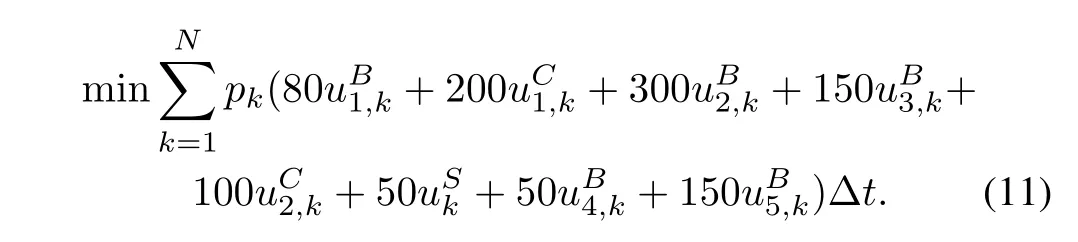
Note in the mineral process,conveyors B1,B2,B3,crushers C1,C2,and the screen have the same operation schedule,i.e., they are switched on at the same time,and switched off at the same time.Similarly,conveyors B4 and B5 must also have the same operating schedule in order to minimise energy cost. Therefore,the following equalities hold:

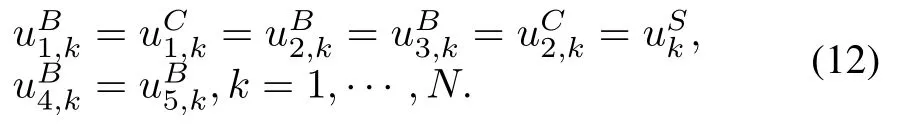
From the mass balance relations,it is reasonable to assume that all minerals fed at conveyor B1 will be fed at the same rateF(t)tons/hour to the 3000 ton stock silo;and similarly, the conveyor B4 must be fed at the rate ofD(t)tons/hour from the stock silo.Then the following mass balance relation at the stock silo can be obtained:

whereM(k)represents the mass of minerals at the stock silo at timek,the initial massM(0)is assumed to be given. Usually the stock silo has a certain capacity constraint for safety reasons,such as the stored minerals at any time must be within the range of 10 tons to 2980 tons.Then the following constraints can be obtained.

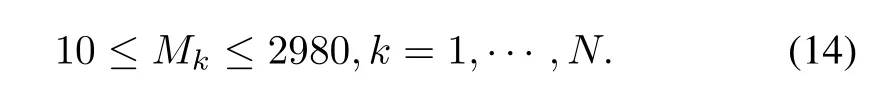
Now the optimisation problem(11)～(14)can be solved to fi nd an optimal on/off status control over the time interval [t0,tN].An MPC algorithm can be easily designed to optimise the on/off scheduling status over the time interval[tk,tN+k]. We would however leave the MPC applications in the following two subsections.

B.Water Puri fi cation System

Fig.2 is an illustration of the water pumping scheme at a water puri fi cation plant in South Africa[11].Water fl ows at the rate of 40mL/day(mega liter per day)from the puri fi cation plant into reservoir R1.The maximum capacity of R1 is 1.4mL,and it is also supplied with water from a fountain at the rate of 5mL/day.The water from R1 is pumped to both reservoir R2 and reservoir R3,with the maximum capacity of 120mL and 60mL,respectively.The water to R2 is pumpedby pumps K1,K2 and K3,each rated at 300kW with the same capacity to pump 22mL/day.Water from R1 to R3 is pumped by pumps G1,G2 and G3,each rated at 275kW with the capacity to pump 10mL/day.R2 and R3 are also supplied by a water utility called Randwater at the cost of ZAR2.98/kL, where ZAR represents the South African currency rand.R3 is also supplied by boreholes at a rate of 10mL/day with the cost of ZAR0.30/kL;water cost from R1 to R2 and R3 has the same rate ZAR1.03/kL.Pumps K3 and G3 are used as back-up pumps and usually are switched off.To simplify the model,it is assumed in[11]that pump G2 keeps running continuously,and pump K2 is chosen as the control object, and the following optimisation model is obtained.

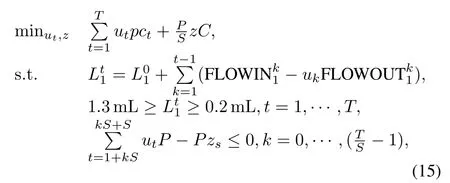
where the two parts in the objective function represent the energy charge and the maximum demand charge,respectively,is the volume of water in reservoir R1 which should always be between 0.2mL and 1.3mL for capacity limit and safety reasons,utis the on/off status of pump K2,S=2, C=ZAR66.5/kW,P=300kW,andzis an intermediate variable which helps to calculate the maximum demand.It is obvious that the constraint about water levels can be derived from the general mass balance constraint in(6).Therefore,this model is a direct application of the general principles in the previous section.Reference[11]further applies MPC to the above problem over a moving horizon of 24 hours.Percentage of savings under benchmarks with the assumptions for real valueut∈[0,1],the open loop control with binary values ofut, and MPC with binary values ofutare compared,and Fig.3 illustrates that MPC and open loop controller have almost the same amount of savings.However,if there is a positive random in fl ow disturbance,i.e.,is replaced by+ 0.2××r(m)withr(m)a random number between 0 and 1,then the open loop solution will violate the reservoir allowable capacity 1.3mL at R1 as shown in Fig.4.Therefore, MPC method will be very helpful to provide a robust solution.

The model in(15)can be further improved by incorporating more control variables and constraints.For instance,all the four pumps G1,G2,K1,K2 can be controlled simultaneously, and the customer water demand can also be considered so as to minimise the supplementary water supply which has a high cost of R2.98/kL.Then the objective function in(15)can be revised as follows.

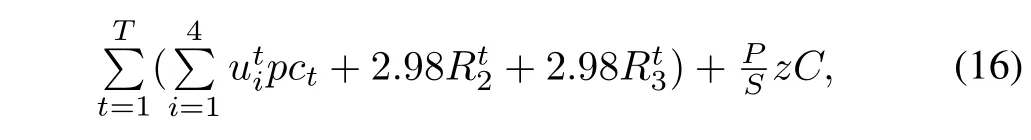
whererepresents the on/off status of the four pumps at timet,andare the amount of supplementary water supplied from the water company Randwater at timetto the reservoirs R2 and R3,respectively.Assume that customer demand at timetfrom reservoirs R2 and R3 areandrespectively.The water levels in R2 and R3 will satisfy similar constraints like those for R1 in(15).For example,the water in R2 must satisfy the following constraint.

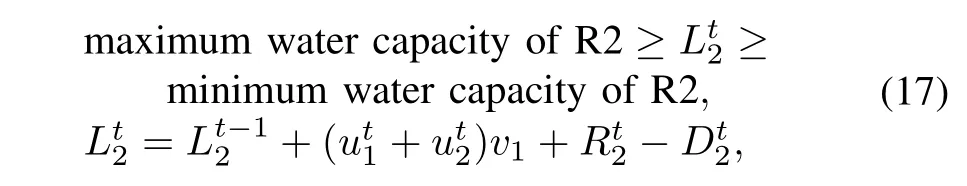
Fig.2.A water pumping system[11].

Fig.3.Comparison of the savings by open loop controller and MPC[11].

Fig.4.Reservoirlevelconstraintviolationofopenloop controllers[11].

whereandare the on/off status of the two pumps K1 and K2,respectively;v1is the amount of water which can bepumped by pump K1 per unit time,which remains the same for pump K2;is the customer water demand from reservoir R2.Note that electricity suppliers often have incentives to industrial customers who are willing to reduce evening peak load,therefore it is proposed to expect the four pumps K1, K2,G1,G2 are not switched on simultaneously at the evening peak period 18:00-20:00.This can be easily formulated as the following logic correlations:

The new model can be further applied in the MPC approach to achieve better energy savings.

C.Plant Maintenance Optimal Scheduling

Generator maintenance optimal scheduling has been studied by many authors;see references listed in[14–15].Similar maintenance scheduling problems exist in many industrial plants.Starting from the model in[14],this subsection proposes an optimisation model to characterise the general plant maintenance scheduling problem.

Assume a plant consists ofndivisions(or units)which need to be regularly maintained.Consider a fi xed time period ofmdays over which an optimal maintenance schedule needs to be found.For simplicity,assume that each division needs to undergo one and only one maintenance within themdays.

Lettrepresent time(in days),andxi,tbe the maintenance state of thei-th division on thet-th day,withxi,t=1 representing thei-th division is under maintenance on thet-th day,whilexi,t=0 has the converse meaning.De fi neyi,tto be the start up state,withyi,tequal to 1 implying that thei-th division has been fi nished maintenance at time(t-1)and is started to work normally at timet.

The objective is to minimise maintenance cost by noting the fact that each division will deliver pro fi ts at any given time, and its closing down for maintenance will cause not only the maintenance cost but also the loss of the corresponding pro fi ts. For this purpose,assume that$pi,tis the pro fi t produced by thei-th division on thet-th day if it is operating normally. Assume that the maintenance cost for divisioniis$aiper day,the starting up cost of divisioniis$bi.Then the objective function is formulated below.

Note that a division under maintenance cannot be started. Therefore the following constraint is obvious.

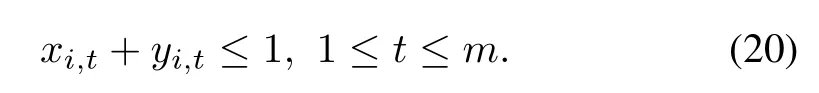
Equation(21)means that the maintenance for divisionineedskidays within themdays,while(22)implies that whenever the maintenance of divisionistarts,it will takekiconsecutive days and no interruption is allowed.

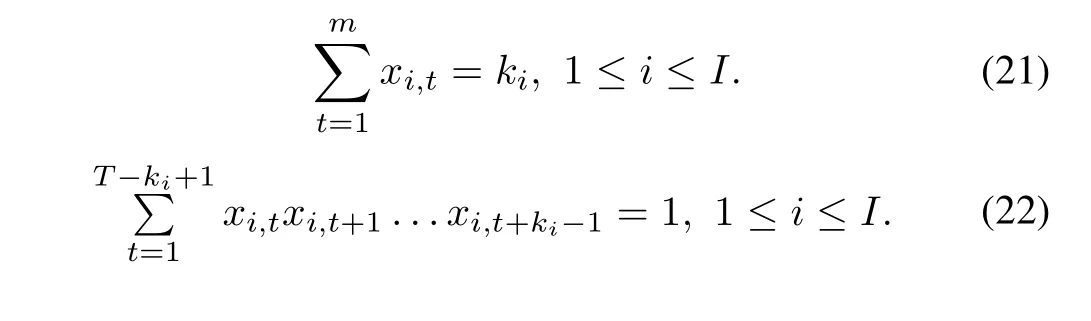
The maintenance on these divisions may be subject to certain logic correlations.For instance,the fi rst two divisions cannot be maintained together(i.e.,at least one of them must be working).This can be written as the following constraint:

Other types of logic correlation constraints can be formulated following the formulae in Section II-A.

The number of maintenance crew needed at any maintenance instant must not exceed the number of available crews:

whereis the number of crew needed for theq-th day of maintenance for thei-th division,andAtis the available number of crew at timet.

There might also be a least requirement on the daily pro fi t produced even some of the divisions are under maintenance. For example,the following inequality indicates that the minimum daily pro fi t should be at least$A.

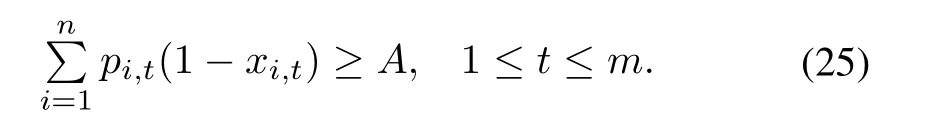
Other system requirements can be added to the above model in order to determine a practically implementable scheduling plan.

The above optimisation model is formulated over the time period fromt=1 tot=m,and it is easily changed into a time period starting from any day for the MPC applications. Dynamic market impact on the pro fi tpi,tcan be easily captured in the MPC approach,therefore,the MPC application will greatly improve the reliability of the above maintenance scheduling model.

IV.CONCLUSIONS

This paper summarises general techniques in energy system operation ef fi ciency modelling and the corresponding model predictive control approach to the obtained energy optimisation models.Examples from mineral processing and plant maintenance are used to illustrate the modelling process, case study on a water pumping system shows further the effectiveness of the model predictive control approach.

REFERENCES

[1]Xia X H,Zhang J F.Energy ef fi ciency and control systems—from a POET perspective.In:Proceedings of the 2010 Conference on Control Methodologies and Technology for Energy Ef fi ciency.Portugal:IFAC, 2010.255-260

[2]Xia X H,Zhang J F,Cass W.Energy management of commercial buildings—a case study from a POET perspective of energy ef fi ciency.Journal of Energy in Southern Africa,2012,23(1):23-31

[3]Xia X H,Zhang J F.Modeling and control of heavy-haul trains.IEEE Control Systems Magazine,2011,31(4):18-31

[4]Xia X H,Zhang J F.Energy auditing-from a POET perspective.In: Proceedings of the 2010 International Conference on Applied Energy. Singapore,2010.1200-1209

[5]Allgo¨wer F,Zheng A.Nonlinear Model Predictive Control.Berlin: Birkha¨user Verlag,2000.

[6]Garc´ıa C E,Prett D M,Morari M.Model predictive control:theory and practice—a survey.Automatica,1989,25(3):335-348

[7]Qin S J,Badgwell T A.A survey of industrial model predictive control technology.Control Engineering Practice,2003,11(7):733-764

[8]Ashok S.Peak-load management in steel plants.Applied Energy,2006, 83(5):413-424

[9]Wu T Y,Shieh S S,Jang S S,Liu C C L.Optimal energy management integration for a petrochemical plant under considerations of uncertain power supplies.IEEE Transactions on Power Systems,2005,20(3): 1431-1439

[10]Badenhorst W,Zhang J F,Xia X H.Optimal hoist scheduling of a deep level mine twin rock winder system for demand side management.Electric Power Systems Research,2011,81(5):1088-1095

[11]van Staden A J,Zhang J F,Xia X H.A model predictive control strategy for load shifting in a water pumping scheme with maximum demand charges.Applied Energy,2011,88(12):4785-4794

[12]Zhang H,Xia X H,Zhang J H.Optimal sizing and operation of pumping systems to achieve energy ef fi ciency and load shifting.Electric Power Systems Research,2012,86:41-50

[13]Xia X H,Zhang J F,Elaiw A.An application of model predictive control to the dynamic economic dispatch of power generation.Control Engineering Practice,2011,19(6):638-648

[14]Ekpenyong U E,Zhang JF,Xia X H.An improved robust model for generator maintenance scheduling.Electric Power Systems Research, 2012,92:29-36

[15]Yamayee Z A.Maintenance scheduling:description,literature survey, and interface with overall operations scheduling.IEEE Transactions on Power Apparatus and Systems,1982,101(8):2770-2779

[16]Zhang J F,Xia X H.A model predictive control approach to the periodic implementation of the solutions of the optimal dynamic resource allocation problem.Automatica,2011,47(2):358-362

Xiaohua Xia Professor in the Department of Electrical,Electronic,and Computer Engineering at the University of Pretoria,South Africa,and the director of both the Centre of New Energy Systems and the National Hub for Energy Ef fi ciency and Demandside Management.He was academically af fi liated with the University of Stuttgart,Germany,the Ecole Centrale de Nantes,France,and the National University of Singapore before joining the University of Pretoria in 1998.He is a fellow of IEEE,a member of the Academy of Science of South Africa,and a fellow of the South African Academy of Engineering.He has been an associate editor or an editorial board member forAutomatica,IEEE Transactions on Circuits and Systems II,IEEE Transactions on Automatic Control,Applied Energy,and specialist editor(control)of theSAIEE Africa Research Journal.His research interests include nonlinear control systems,and energy systems.

Jiangfeng Zhang obtained the B.Sc.and Ph.D. degrees in computing mathematics from Xi′an Jiaotong University,China in July 1995 and December 1999,respectively.From February 2000 to August 2002,he was a lecturer at the Shanghai Jiao Tong University.Then he was a postdoctoral researcher in the Chinese University of Hong Kong,Ecole Centrale de Nantes,Nanyang Technological University,University of Liverpool,and the University of Pretoria.He was a senior lecturer and then an associate professor in the Department of Electrical, Electronic,and Computer Engineering at the University of Pretoria from 2008 to 2013.He is now a senior lecturer in the Department of Electronic and Electrical Engineering,University of Strathclyde.His research interests include energy management and control theory.

t

June 26,2013;accepted August 31,2013.This work was supported by National Research Foundation of South Africa(UID85783), the National Hub for Energy Ef fi ciency and Demand Side Management and Exxaro.Recommended by Associate Editor Fei-Yue Wang.

:Xiaohua Xia,Jiangfeng Zhang.Operation ef fi ciency optimisation modelling and application of model predictive control.IEEE/CAA Journal of Automatica Sinica,2015,2(2):166-172

Xiaohua Xia is with the Department of Electrical,Electronic and Computer Engineering,University of Pretoria,Pretoria 0002,South Africa(e-mail: xxia@postino.wp.ac.za).

Jiangfeng Zhang is with the Department of Electronic and ElectricalEngineering,UniversityofStrathclyde,G11XW,UK(e-mail: jiangfeng.zhang@strath.ac.uk).