Consensus Seeking for Discrete-time Multi-agent Systems with Communication Delay

Zhenhua Wang,Juanjuan Xu,and Huanshui Zhang

Consensus Seeking for Discrete-time Multi-agent Systems with Communication Delay

Zhenhua Wang,Juanjuan Xu,and Huanshui Zhang

—This paper studies the consensus problem for discrete-time multi-agent systems of fi rst-order in the presence of constant communication delay.Provided that the agent dynamics is unstable and the network topology is undirected,effects of two kinds of communication delays on consensus are investigated. When the relative information is affected by delay,we show that the effect of delay can be alleviated by using the historical input information in the protocol design.On the other hand,if the communication delay only in fl uences the actually transmitted information,suf fi cient condition admitting any large yet bounded delay for consensus is obtained,and the delay in this case is allowed to be unknown and time-varying.Finally,simulation results are provided to demonstrate the effectiveness of the theoretical results.

Index Terms—Multi-agent systems,consensus protocol,communication delay,eigenratio.

I.INTRODUCTION

IN recent years,growing attention has been attracted in studying the consensus problem due to a broad application of multi-agent systems,including automatic control[1],distributed estimation[2]and fl ocking[3],etc.Generally speaking, consensus means that several autonomous agents reach an agreement regarding a certain quantity of interest.Currently, many results on consensus have been obtained.For the Vicsek′s model[4],where all the agents moved in the plane at the same speed but with different headings,its theoretical explanation for the consensus behavior was provided in[5]. Given a time-varying interconnection topology,[6]investigated a group of autonomous agents tracking an active leader by constructing a neighbor-based state-estimation rule.The necessary and suf fi cient condition on consensus for general discrete-time linear systems was given in[7].

Delay effect on the convergence of consensus is an important issue to be considered.Naturally,the communication delay appearing in the network hinders the information being transmitted from one agent to another[8].So far,many researchers have studied the effect of communication delay on agents′consensus behavior.It was shown in[9]that singleintegrator agents subjected to constant communication delay can achieve consensus if and only if the delay is bounded by a maximum.Given a directed and dynamically changingtopology,[10]investigated the effect of communication delay that only affected the actually transmitted information on consensus.Reference[11]provided a necessary and suf fi cient condition to guarantee quasi-consensus and consensus with the distributed delay in the control input.Assuming that the agent dynamics is at most polynomially unstable,consensus for high-order linear multi-agent systems with delays in both the communication and input was studied in[12].To the best of our knowledge,the relevant results in the context of discrete-time agents are rare since delay effects signi fi cantly complicate the problem.For the scalar agent dynamics that is critically unstable,[13]considered the consensus of multiagent systems with communication delay.Reference[14] studied the existence of maximum delay margin of input delay for the general scalar discrete-time agents to achieve consensus.Under the assumption that neighbors′measured output information can be received by agents,consensus problem of the network with communication delay was studied in[15].A constrained consensus problem requiring every agent to lie in a closed convex set was addressed in[16] over the network with communication delay.Provided that all eigenvalues of the system matrix were in the closed unit disc,[17]investigated the consensus of high-order multi-agent systems in the network with constant communication delay.

In this paper,we investigate the in fl uences of two kinds of communication delays on consensus for unstable discretetime multi-agent systems.If the delay only affects the relative information that is transmitted,the methods used in[13] and[17]are unavailable due to the system is unstable.The technique in[14]cannot work when the delay is much large. On the other hand,in case that the communication delay only in fl uences the actually transmitted information,the frequencydomain approach used in[13]is helpless to the time-varying delay.

The main contribution of this paper are twofold.First,for any large yet bounded communication delay that affects the relative state information,consensus condition is given under the assumption that the network topology is exactly known. Second,if the delay only in fl uences the actually transmitted information,a suf fi cient condition related to agent dynamics and network topology is shown for any large yet bounded delay to achieve consensus,and especially the delay in this case is allowed to be unknown and time-varying.

The remainder of this paper is organized as follows.In Section II,some preliminaries of the algebraic graph theory are presented.The consensus problem to be studied is formulated in Section III.In Section IV,consensus analysis of multiagent networks with two kinds of communication delays are respectively presented in detail.Following that,Section V provides two simulation examples.Finally,conclusions are reported in Section VI.

The following notations will be used throughout this paper. Symbols R and Z+respectively denote the sets of real numbers and positive integers.For any positive integerN∈Z+, letN:={1,2,···,N}andINbe an identity matrix with dimensionN×N.Notation diag{a1,a2,···,aN}denotes a diagonal matrix.Given that 1Nis anNdimensional vector with all ones andis the Euclidean norm.For a scalarr＞0,letCrrepresent the Banach space of continuous-time scalar functions mapping the interval{-r,-r+1,···,0}into R.

II.PRELIMINARIES

In this section,a brief introduction to the algebraic graph theory is provided.

LetG=(V,E,A)be a weighted undirected network of orderN,whereV={1,2,···,N}is the set of nodes;E=V×Vis the set of edges andA=[aij]∈RN×Nis the weighted adjacency matrix with symmetric nonnegative elements.Assumeaij＞0 if and only if(i,j)∈E, i.e.,information can be exchanged between nodesiandj. Moreover,supposeaii=0 for alli∈V.An undirected graphGis connected if there exists a path between any pair of distinct nodesiandj(j∈N).The degree of nodeiis de fi ned asdi:=and we introduce anN×Ndiagonal matrixD=diag{d1,···,dN}as the degree matrix ofG. Then the Laplacian matrix ofGis de fi ned asLG:=D-A. Obviously,matrixLGis symmetric and 1Nis its eigenvector corresponding to eigenvalue 0.IfGis connected,all the eigenvalues ofLGare positive except one 0 eigenvalue and can be written as 0=λ1＜λ2≤···≤λN.In addition, the eigenratiois an important factor[7,18],and a larger eigenratio corresponds to a better synchronizability of the underlying communication graph.If every node can directly communicate with other nodes in the network,i.e.,(i,j)∈Efor,then the graph is called complete.Especially,the eigenratio=1 in the complete case.

III.PROBLEM STATEMENT

In this paper,assume all the agents considered have the following dynamics

wherexi(k)∈R andui(k)∈R are the state and control input of agenti,respectively.The coef fi cients satisfya∈R,b∈R andb/=0.In addition,assumexi(0)are known initial values.

Regarding the aboveNagents as nodes in a network,the information fl ow between two agents can be regarded as a path between the nodes.Thus,the interconnection topology in multi-agent systems can be conveniently captured by an undirected graphG=(V,E,A)withV={1,2,···,N}andA=[aij]∈RN×N.

Note that the communication delay is common in network control.Letd∈Z+denote the delay during the information communication.Making use of the relative state information, the commonly used protocol[9,17]is described as

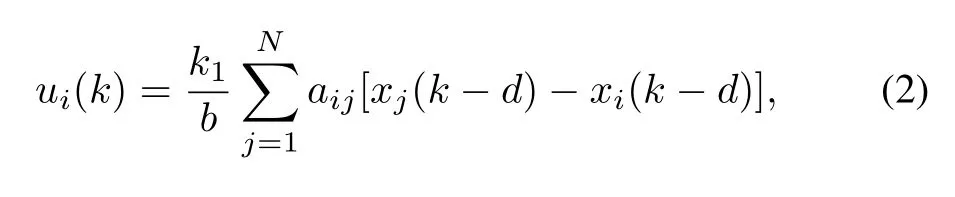
wherek1is a fi xed control gain and independent of the indexi.

In case the network topology is exactly known,we design the following protocol to eliminate the effect of delay on consensus

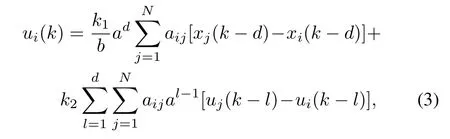
wherek1,k2are fi xed control gains and are independent of agent′s indexi.

Remark 1.It should be noted that the designing of protocol (3)adopts the predictor-like technique,which is inspired by the famous Smith predictor[19],the fi nite spectrum assignment method[20]and the Artstein reduction[21].

Remark 2.In the designing of protocol(3),we assume that the constant communication delay is exactly known.However, in case that the constant delay is unknown,we can get the delay information by the method of“time-stamping”in[22], i.e.,all the transferred information is marked with the time when it was generated,then the time delay can be calculated by comparing the“time stamp”with the local clock.

Remark 3.In protocol(3),the distributed historical input information are used in the protocol design.In fact,comparing with the relative state information,agent′s own state information cannot be used directly.However,it is feasible for agent to acquire its own historical input information.Thus,every agent can transmit its own historical input information to neighbors directly on the condition that the network topology is exactly known.It should be noted that similar protocol named as predictor feedback protocol has been given in[12].Besides, literature[23]has also used the relative input information in the protocol design.

To further show the reasonability of the designed protocol (3),we give a physical example as follows.

Suppose there areNaircrafts fl ying in the same direction with dynamics

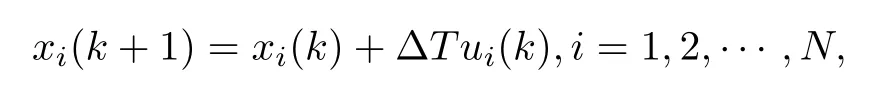
where ΔT＞0 is sampling time.It is known that formation keeping for aircrafts is an important issue in reality.As a special case,this example aims to guarantee that the distance between any two aircrafts is zero along the fl ying direction. Assumexi(k)is the position of thei-th aircraft,andui(k)is the corresponding velocity controller[24].In the fl ying direction,considering that the relative position detected by aircrafts are delayed by constantd,i.e.,To eliminate the effect of delay on the aim above,every pilot in the aircraft is required to send part of historical velocities to neighbors.

If the communication delay only affects the actually transmitted information as in[10]and[13],we design the following protocol

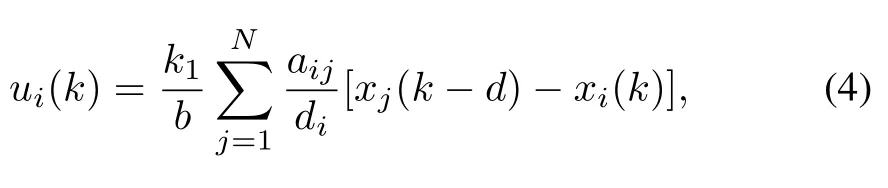
whered∈Z+is the communication delay,anddi=is the degree of agenti.

Without loss of generality,we additionally set the initial valuesxi(θ)=0 andui(θ)=0 for anyθ＜0 to make the systems(1)operational under above given protocols.The de fi nition of consensus is shown as follows.

De fi nition 1.Given an undirected graphG,the discrete-time multi-agent systems(1)are said to achieve consensus under the designed protocols above if for any fi nite initial values,the states of all agents satisfy0 ask→∞fori,j∈N.

From above de fi nition,it is obvious to know that the consensus problem can be solved when the systems(1)are stable by takingui(k)≡0.In this paper,we focus on unstable multi-agent systems,i.e.,|a|≥1 in(1)to make the problem interesting.The problems studied in this paper are as follows

1)Provide conditions such that multi-agent systems(1) achieve consensus under protocols(3)and(4),respectively.

2)Comparing with the commonly used protocol(1),show the advantage of the designed protocol(3).

Remark 4.The problem studied in this paper is more general than those investigated in[7,13]and[17].In fact, [7]concerns consensus without time delay;[13]is limited to time-invariant delay and[17]focuses on the systems that are at most critically unstable.

IV.MAIN RESULTS

In this section,only the case ofa≥1 in(1)is considered, and the results fora≤-1 can similarly be obtained.Before presenting our main results,we fi rst show the following technical lemmas.

A.Lemmas

The following lemma can be found in[25].

Lemma 1.Consider a retarded difference equation

wherexk(s)=x(k+s),ands∈{-r,-r+1,...,0}.The functionf:R×Cris such that the image byfof R×(a bounded subset ofCr)is a bounded subset of R and the functionsu,v,w,p:R+→R+are continuous and strictly increasing functions,withu(0)=v(0)=0 andp(t)＞tfor anyt＞0.Suppose that there is a continuous functionV:R→R,such that for allx∈R the following conditions are satis fi ed,

Then the retarded difference equation is globally uniformly asymptotically stable.

From Lemma 1,we can get the following lemma,which plays an important role in this section.

Lemma 2.For the discrete-time delayed systemη(k+1)=fη(k)+gη(k-d),wheref∈R,g∈R are constants,if|f|+|g|＜1,the delayed system is asymptotically stable atη(k)≡0.

Proof.Ifg=0,it is obvious that limk→∞η(k)=0 from|f|＜1.Without loss of generality,in the following we assumeg/=0.Take a functionV(η(k))=|η(k)|.Then

there exists constantr∗＞0 such that the delayed system is not asymptotically stable for any choice of the feedback gainαif the delayr≥r∗.

B.Consensus Results

Now,we are in position to give the main results of this paper.We fi rst show the consensus result of multi-agent systems(1)witha＞1 under protocol(3).

Proof.Inserting protocol(3)into systems(1)follows

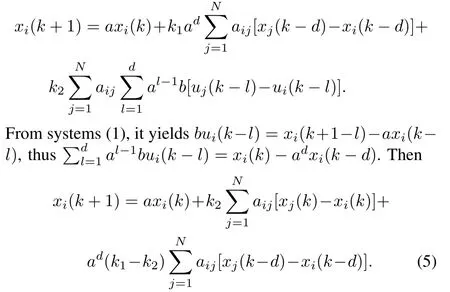
Letx(k):=[x1(k),···,xN(k)]T.Based on(5),the dynamical equation ofx(k)can be written as

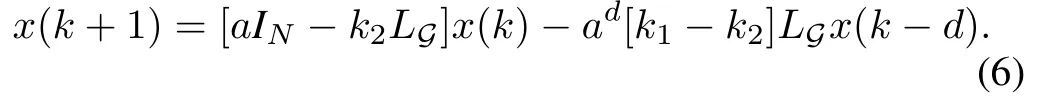
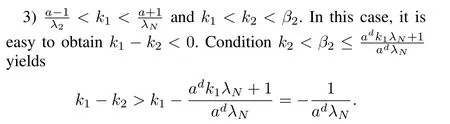
Thus,0＜ad|k2-k1|λN＜1.Similarly as proven in 1), consensus can be guaranteed.□

Remark 5.It is shown in Theorem 1 that the consensus condition is related toi.e.,the eigenratio of undirected graphG.Thus,the more unstable are the multi-agent systems, the bigger eigenratio corresponding a topology with better synchronizability is needed to guarantee consensus.Especially, when the undirected graphGis completed,any unstable agent dynamics is allowed for consensus by the method in Theorem 1.

Whena=1,the above method is also applicable,and we give the following corollary.

Proof.The proof is similar to Theorem 1 and omitted for simplicity.□

To show the advantage of protocol(3),we investigate the consensus problem of multi-agent systems(1)witha＞1 under the commonly used protocol(2).

Theorem 2.For any connected undirected graphG,the multi-agent systems(1)cannot achieve consensus under protocol(2)for any gaink1∈R if the communication delay is large enough.

Proof.From protocol(2)and systems(1),we get

By the method in Theorem 1,it yields that the consensus is achieved if and only if the error system

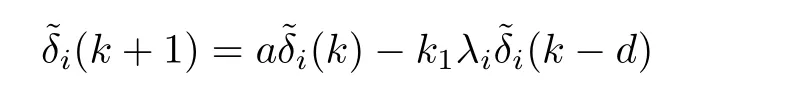
is stable simultaneously fori∈{2,···,N}.Due toa＞1 and in view of Lemma 3,the proof is completed.□

Remark 6.It is known from Theorem 2 that the communication delay indeed affects consensus.However,the results in Theorem 1 show that the effect of delay on consensus can be eliminated if the network topology is exactly known and every agent transmits historical input information to neighbors.

In the following,we are to state the consensus result of the discrete-time multi-agent systems(1)under protocol(4).

When the undirected graphGis connected,we know that matrix[D-1A]is anN×Nirreducible stochastic matrix[26], and there is a unique invariant probability vectorα= [α1,α2,···,αN]Twithαi＞0,∀i∈Nandsuch thatαT[D-1A]=αT.In the following,letµi,i∈Ndenote the eigenvalues of matrix[D-1A].It is known from Lemma 1 in[27]that matrix[D-1A]has a simple eigenvalueµ1=1 if the undirected graphGis connected,and other eigenvalues are real with modulus no bigger than 1.Without loss generality,letµN=max{|µi|,i=2,···,N}.Now,we state the following result.

Remark 7.The condition for consensus becomes 1≤a＜Nif the network topology in Theorem 3 is complete,whereNis the number of the agents in the network.In fact,when the undirected graphGin Theorem 3 is complete,the eigenvalues of matrix[D-1A]satisfyµ1=1 andµ2=···=µN=

Remark 8.It should be noted that the communication delay in protocol(4)is allowed to be unknown.In fact,from the proof of Theorem 3,the precise information of the delay or the historical input information of agents is not needed.In addition,Lemma 1 and the proof of Theorem 3 admit the communication delay to be time-varying in protocol(4)by using exactly the same method in Theorem 3.

V.SIMULATIONS

In this section,two examples are carried out to verify the theoretical results obtained by the previous analysis.

Consider a network consisting of 4 agents indexed by 1,2,3, 4,respectively.The topology among those agents is described by an undirected graphG={V,E,A},whereV={1,2,3,4}. The adjacency matrix and Laplacian matrix are described as

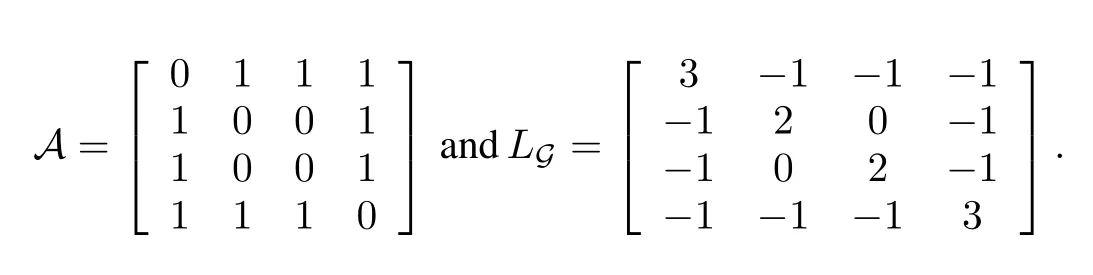
Clearly,undirected graphGis connected and the nonzero eigenvalues ofLGareλ2=2,λ3=4 andλ4=4.Under the connected undirected graphG,we consider the following two examples.

Example 1.Assumea=2,b=2 in the discretetime agent dynamics(1).Let the initial values be given asx(0)=[8,2,-4,8]Tandxi(s)=0,ui(s)=0 for anys＜0. Given the communication delayd=4,make use of protocol (3)and take gainsk1=0.6 andk2=0.606 in view of Theorem 1,then Fig.1 shows the asymptotic stability of the error systems,where(k)=[x1(k)+x2(k)+x3(k)+x4(k)].

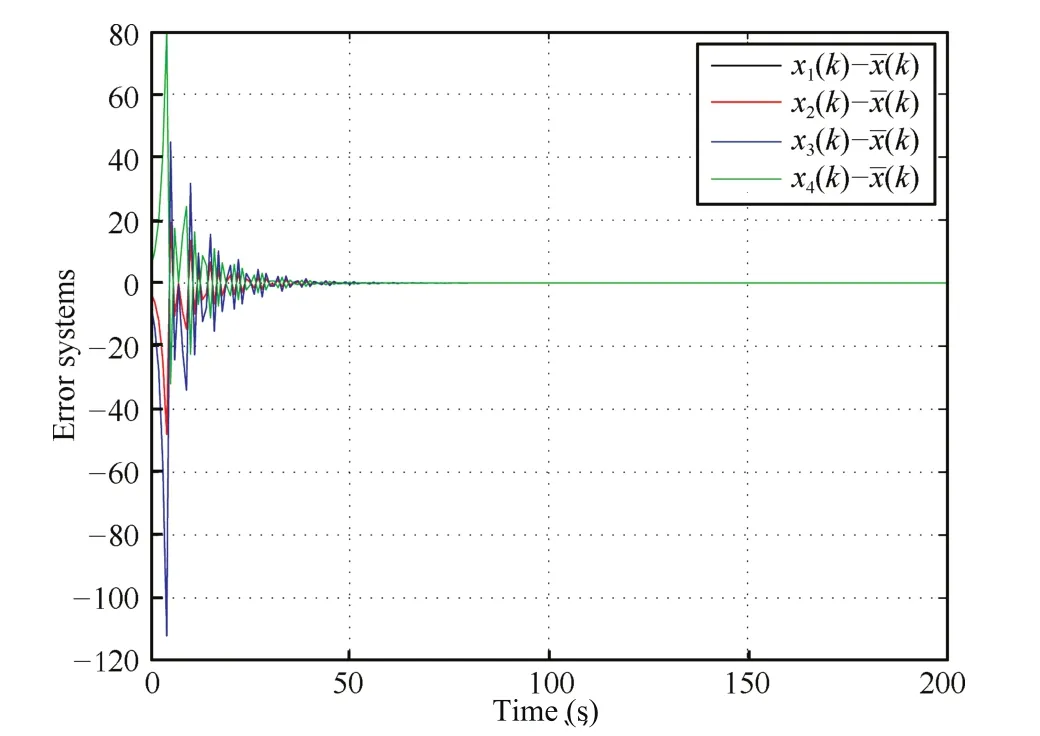
Fig.1.Example 1.

where［4sin2(k)］represents to the integer part of timevarying communication delay 4sin2(k).From Theorem 3, take consensus gaink1=1.31,then for the given initial valuesx(0)=[10,-2,5,20]Tandxi(s)=0(s＜0),Fig.2 reveals the error systems converge to zero asymptotically, where(k)=0.3x1(k)+0.2x2(k)+0.2x3(k)+0.3x4(k) denotes the weighted average state of all agents.

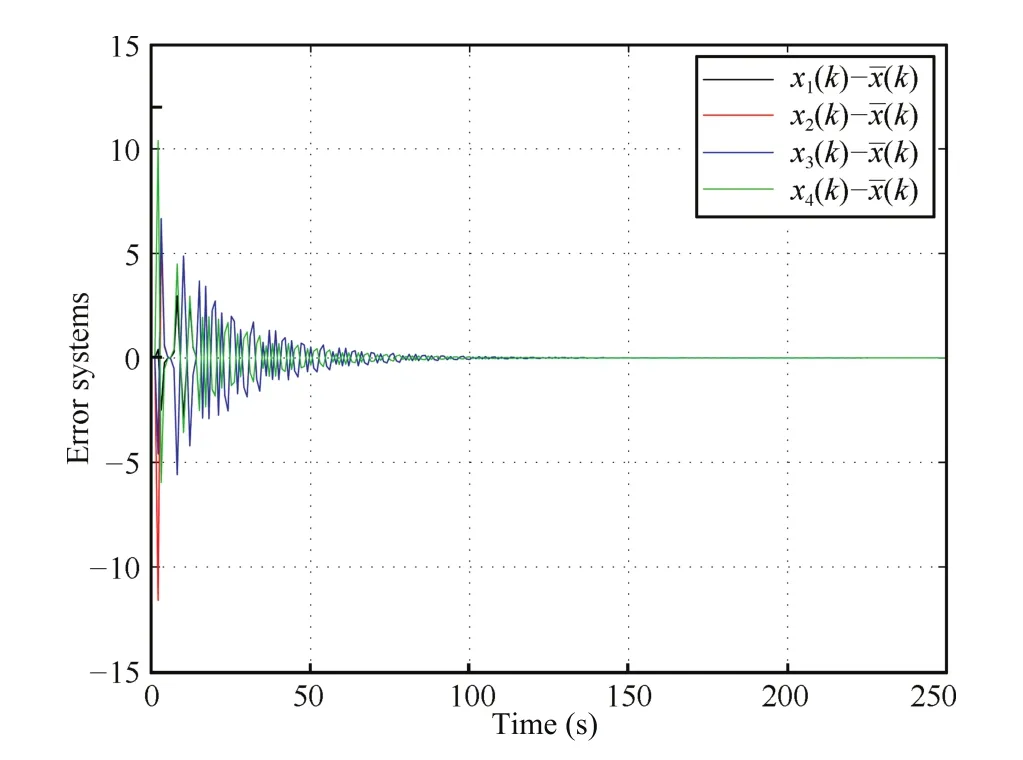
Fig.2.Example 2.

VI.CONCLUSION

This paper addresses the consensus problem for unstable discrete-time multi-agent systems with two kinds of communication delays,which only affect the relative information and the actually transmitted information,respectively.The effect of the fi rst kind of communication delay is eliminated if the network topology is exactly known.Suf fi cient condition for consensus is provided in case of the second communication delay,where the delay is also allowed to be unknown and timevarying in this case.It is worth mentioning that the proposed results are expected to extend to the vector state and the timevarying topology.

REFERENCES

[1]Pettersen K,Gravdahl J T,Nijmeijer H.Group Coordination and Cooperative Control.Berlin:Springer,2006.

[2]Cao Y C,Ren W,Meng Z Y.Decentralized fi nite-time sliding mode estimators and their applications in decentralized fi nite-time formation tracking.System&Control Letters,2010,59(9):522-529

[3]Yu W W,Chen G R,Cao M.Distributed Leader-follower fl ocking control for multi-agent dynamical systems with time-varying velocities.System&Control Letters,2010,59(9):543-552

[4]Vicsek T,Czir´ok A,Ben-Jacob E,Cohen I,Shochet O.Novel type of phase transition in a system of self-driven particles.Physical Review Letters,1995,75(6):1226-1229

[5]Jadbabaie A,Lin J,Morse A S.Coordination of groups of mobile automous agents using nearest neighbor rules.IEEE Transactions on Automatic Control,2003,48(6):998-1001

[6]Hong Y G,Wang X L.Multi-agent tracking of a high-dimensional active leader with switching topology.Journal of Systems Science and Complexity,2009,22(4):722-731

[7]You K Y,Xie L H.Network topology and communication data rate for consensusability of discrete-time multi-agent systems.IEEE Transactions on Automatic Control,2011,56(10):2062-2075

[8]Tian Y P,Liu C L.Robust consensus of multi-agent systems with diverse input delays and asymmetric interconnection perturbations.Automatica, 2009,45(5):1347-1353

[9]Olfati-Saber R,Murray R M.Consensus problems in networks of agents with switching topology and time-delays.IEEE Transactions on Automatic Control,2004,49(9):1520-1533

[10]Moreau L.Stability of continuous-time distributed consensus algorithms. In:Proceedings of the 43rd IEEE Conference on Decision and Control. Nassau:IEEE,2004.3998-4003

[11]Yu W W,Chen G R,Cao M,Ren W.Delay-induced consensus and quasi-consensus in multi-agent dynamical systems.IEEE Transactions onCircuitsandSystems,PartI:RegularPaper,2013,60(10):2679-2687

[12]Zhou B,Lin Z L.Consensus of high-order multi-agent systems with large input and communication delays.Automatica,2014,50(2): 452-464

[13]Tian Y P,Liu C L.Consensus of multi-agent systems with diverse input and communication delays.IEEE Transactions on Automatic Control, 2008,53(9):2122-2128

[14]Xu J J,Zhang H S,Xie L H.Input delay marigin for consensusability of multi-agent systems.Automatica,2013,49(6):1816-1820

[15]Tan C,Liu G P.Consensus of discrete-time linear networked multi-agent systems with communication delays.IEEE Transactions on Automatic Control,2013,58(11):2962-2968

[16]Lin P,Ren W.Constrained consensus in unbalanced networks with communication delays.IEEE Transactions on Automatic Control,2014, 59(3):775-781

[17]Wang X,Saberi A,Stoovogel A A,Grip H F,Yang T.Synchronization in a network of identical discrete-time agents with uniform constant communication delay.International Journal of Robust and Nonlinear Control,2013,24(18):3076-3091

[18]Barahona M,Pecora L M.Synchronization in small-word systems.Physical Review Letters,2002,89(5):054101

[19]Smith O.Controller to overcome dead time.Instrument Society of America-Journal,1959,6(2):28-33

[20]Manitius A,Olbrot A.Finite spectrum assignment problem for systems with delays.IEEE Transactions on Automatic Control,1979,24(4): 541-553

[21]Artstein Z.Linear systems with delayed control:a reduction.IEEE Transactions on Automatic Control,1982,27(4):869-879

[22]Hua J W,Liang T,Sun H X,Lei Z M.Time-delay compensation control of networked control systems using time-stemp based state prediction.In:Proceedings of the 2008 ISECS International Colloquium on Computing,Communication,Control,and Management.Washington, DC,USA:IEEE,2008.198-202

[23]You K Y,Xie L H.Coordination of discrete-time multi-agent systems via relative output feedback.International Journal of Robust and Nonlinear Control,2011,21(13):1587-1605

[24]Ren W,Atkins E.Distributed multi-vehicle coordinated control via local information exchange.International Journal of Robust and Nonlinear Control,2007,17(10-11):1002-1033

[25]Lin Z L.On asymptotic stabilizability of discrete-time linear systems with delayed input.Communications in Information and Systems,2007, 7(3):227-264

[26]Fang H T,Chen H F,Wen L.On control of strong consensus for networked agents with noisy observations.Journal of Systems Science and Complexity,2012,25(1):1-12

[27]Zeng L,Hu G D.Consensus of linear multi-agent systems with communication and input delays.Acta Automatica Sinica,2013,39(7): 1133-1140

Juanjuan Xu received the B.E.degree in mathematics from Qufu Normal University in 2006,and M.E.degree in mathematics in 2009 from Shandong University,and the Ph.D.degree in control science and engineering in 2013 from Shandong University,then worked as postdoctoral researcher at the School of Control Science and Engineering, Shandong University.Her research interests include distributed consensus,optimal control,game theory, stochastic systems,and time-delay systems.

Huanshui Zhang graduated in mathematics from Qufu Normal University in 1986 and received his M.sc.and Ph.D.degrees in control theory from Heilongjiang University,China,and Northeastern University,China in 1991 and 1997,respectively. He worked as a postdoctoral fellow at the Nanyang Technological University from 1998 to 2001 and research fellow at Hong Kong Polytechnic University from 2001 to 2003.He is currently a Changjiang Professor at Shandong University,China.His research interests include optimal estimation,robust fi ltering and control,time delay systems,singular systems,wireless communication and signal processing.Corresponding author of this paper.

ang

the B.E.degree in mathematics from Jinan University in 2008,and M.E. degree in mathematics in 2011 from Shandong University.Since 2011,he is a Ph.D.candidate with the school of Control Science and Engineering, Shandong University,China.His research interests include multi-agent systems,networked control systems,and time-delay systems.

Manuscript received June 10,2014;accepted November 17,2014.This work was supported by the Taishan Scholar Construction Engineering by Shandong Government,the National Natural Science Foundation of China (61034007,61120106011,61203029,61304045,61403235).Recommended by Associate Editor Jie Chen.

:Zhenhua Wang,Juanjuan Xu,Huanshui Zhang.Consensus seeking for discrete-time multi-agent systems with communication delay.IEEE/CAA Journal of Automatica Sinica,2015,2(2):151-157

Zhenhua Wang,Juanjuan Xu,and Huanshui Zhang are with the School of Control Science and Engineering,Shandong University,Jinan,Shandong,250061,China(e-mail:wzhua111@126.com;jnxujuan@163.com; hszhang@sdu.edu.cn).