Robust Control of Permanent Magnet Synchronous Motors
2015-08-09ZhenhuaDengandXiaohongNian
Zhenhua Deng and Xiaohong Nian
Robust Control of Permanent Magnet Synchronous Motors
Zhenhua Deng and Xiaohong Nian
—In this paper,permanent magnet synchronous motors(PMSMs)are investigated.According to the feature of PMSMs,a novel state equation of PMSMs is obtained by choosing suitable state variables.Based on the state equation,robust controllers are designed via interval matrix and PI control idea. In terms of bilinear matrix inequations,suf fi cient conditions for the existence of the robust controller are derived.In order to reduce the conservation and the dependence on parameter, the control inputs of PMSMs are divided into two parts,a feedforward control input and a feedback control input,and relevant suf fi cient conditions for the existence of the controller are obtained.Because of the suitable choice of state variables,the proposed control strategies can cope with the load uncertainty and have robustness for disturbance.Finally,simulations are carried out via Matlab/Simulink soft to verify the effectiveness of the proposed control strategies.The performance of the proposed control strategies are demonstrated by the simulation results.
Index Terms—Bilinear matrix inequality(BMI),interval matrix,permanent magnet synchronous motor(PMSM),robust control.
I.INTRODUCTION
PERMANENT magnet synchronous motors(PMSMs) have been widely used in the motion control fi eld, transmission control fi eld,servo system and so on,thanks to theirs features of small volume,high power,low noise and high torque-to-current ratio.Compared with other motors,the PMSMs have many advantages,but theirs mathematical model has the characteristics of high order,nonlinear,strong coupling and multi-variables.Therefore,it is dif fi cult to design theirs controller.Because the PMSMs has an irreplaceable role in engineering application,huge economic bene fi t will be achieved and good motion/traction performance will be obtained if it has been well controlled.An increasing number of scholars came up with all kind of control strategies in this fi eld in recent decades of years.For example,in order to deal with thedisturbance of parameter and load torque,robust control[1-2]was developed.Adaptive control[3-4]has been researched so that the controller can adapt to the change of parameter and/or load.In[5-6],some performance indexes were optimized when predictive control was used.In order to get good output performance even the motor′s parameters change with time, model reference adaptive control[7]was introduced in this fi eld.Sensorless controller[8]and observer-based[9]controller were designed to reduce the cost of controller and minimize the volume of controller.Fuzzy controller[10-11]was widely used to handle the structured and unstructured uncertainty.In order to deal with the disturbances,slide mode controller[12]has been researched.Internal model control was utilized to improve the robustness of the whole system[13].In[14], torque feedforward controller was established to achieve good dynamic performance.Besides,many other control strategies were developed,such as near optimal control[15]and neural network control[16].Recently,hybrid control methods[10,13]have been widely adopted.
Interval matrix is often used to cope with systems′parameters are unknown but vary(or locate)in a certain range[17-18]. Its mainly idea is an interval matrix whose elements change(or locate)in a speci fi c range can be expressed by several matrices which can be further handled by other methods.For a given PMSM,restricted by supply power,operation environment, protection equipment and so on,current and speed are and must be in a speci fi c range likes rated range.Therefore, interval matrix can be introduced to design the controller of PMSMs.Besides,although many control strategies have been developed,in fact,PI control method is still a main control strategy in engineering application because it is easy to implement and has a good control performance,i.e.,many advance control strategies have not been widely adopted in engineering because it is not easy to apply or its cost is higher than that of the conventional PI control method.In order to get a easy realized controller which can deal with load uncertainty, in this paper,robust controllers are developed via interval matrix and PI control idea.
This paper is organized as follows.In Section II,the mathematical model of PMSMs and lemmas are presented. Robust control strategies are developed in Section III.To verify the effectiveness of the proposed methods,in section IV,simulations are carried out via Matlab/Simulink soft.In Section V,some conclusions are obtained.
II.MODELDESCRIPTION ANDLEMMAS
According to[19-20],the mathematical model of PMSMs can be expressed as

whereLsd,Lsqared-andq-axis inductance;Rsis stator resistances;ψris permanent magnet fl ux linkage;npis the number of pole pairs;Bfis frictional coef fi cient;Jis moment inertia;idandiqared-andq-axis stator currents;ωis rotor angular velocity;udanduqared-andq-axis voltages andTlis load torque.
Usually,the model expressed as(1)could not accurately describe the actual model of PMSMs because of the existence of disturbance.For example,resistance will increase with the rise of temperature.In other words,disturbances must be considered in the model to make the model more accurately present the actual model.Thus,the following model is established if disturbances are considered.
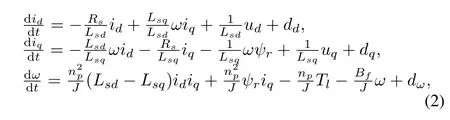
wheredd,dqanddωrepresent the total disturbances acting ond-axis,q-axis and motion equations,respectively,which may be caused by the environment or the change of parameter.And in fact,the disturbances and the load change very slowly,i.e., the following equations usually are satis fi ed.
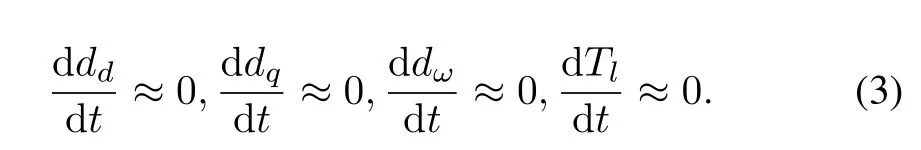
Lemma 1[21].For any scalarε>0,XandYare real matrices with appropriate dimensions so that the following inequality is obtained.

Lemma 2[22].Given symmetric matrix

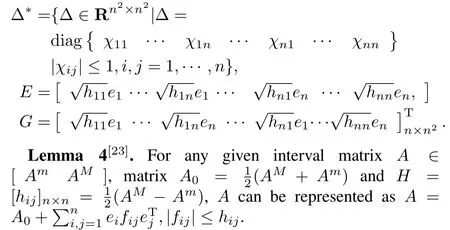
Notations.Iis identity matrix with appropriate dimension andeiis theithcolumn of unit matrix with appropriate dimension.X<Y,whereXandYare symmetric matrices, means that the matrixY-Xis positive de fi nite.
III.ROBUST CONTROL
Although many advance control strategies have been developed in the PMSMs control fi eld,PI controller is still currently main control strategy in practical application because it is easy to implement and can get good control performance. Therefore,in this section,robust controllers of PMSMs will be developed via PI control idea.
A.Robust Controller
According to the character of PMSMs,the state variables and control inputs can be chosen as

whereω∗is the desired speed of the system,and is a constant.
According to(2)~(4),the following state equation is obtained.

where

For a given PMSM which is constrained by the voltage source,switch frequency,protect facilities,operating environment and so on,current and speed are and must be in a certainrange,such as rated range.In other words,current is not larger than rated current and speed is not higher than rated speed. Hence,the following assumptions are reasonable.

whereandωMare the lower bound and the upper bound ofid,iqandω,respectively.
Based on condition(6),A(t)is viewed as interval matrix, and according to Lemma 3,A(t)can be rewritten as

The following theorem can be obtained.
Theorem 1.The PMSMs presented as(2)can be stabilized and the rotor angular speed can track the desired speed under the conditions(3)and(6)if there exist a symmetric and positive-de fi nite matrixP1∈R5×5,matrixK∈R2×5and positive scalarεsuch that the following BMI holds:

And the robust control law is=KX.
Proof.The control law is designed as

Choose Lyapunov function as follows.

Taking the derivative of Lyapunov function(10)with respect totalong system(5)with(7)yields
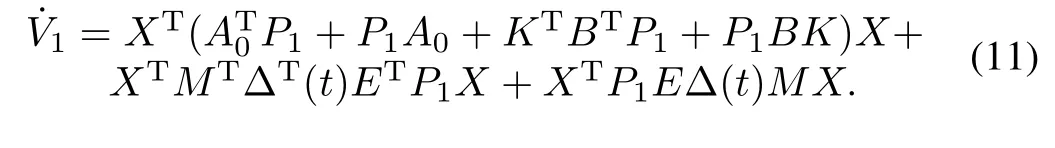
Equation(11)can be written as follows via Lemma 1 and Δ(t)TΔ(t)≤I.

IfQ1<0,the time derivative of Lyapunov functionV1is negative,which means the system can be stabilized by the controller and the PMSMs′speed can follow the desired speed according to Lyapunov stability theory.AndQ1<0 can be expressed as(8)by Lemma 2.□
There are six interval variable in matrixA(t),i.e.,a23,a25,a32,a35,a52anda53.The matrixA(t)can be rewritten as follows via Lemma 4 to reduce the conservative of BMI.

The following theorem can be obtained.
Theorem 2.The PMSMs presented as(2)can be stabilized and the rotor angular speed can track the desired speed under the conditions(3)and(6)if there exist symmetric and positivede fi nite matrixP2∈R5×5,matrixK∈R2×5,real scalarε23>0,ε25>0,ε32>0,ε35>0,ε52>0 andε53>0 such that the following BMI holds:
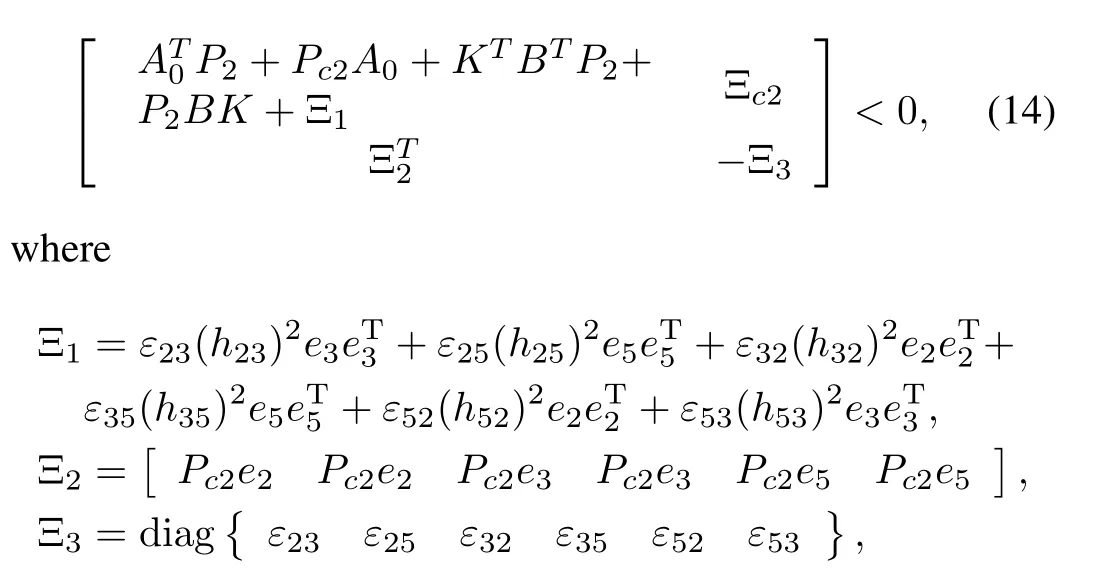
and the robust control law is˙U=KX.
Proof.Lyapunov function is designed as

Taking the derivative of Lyapunov function(15)with respect totalong system(5)with(13)yields
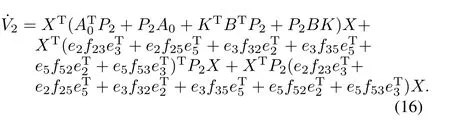
According to Lemma 1 andfijTfij≤(hij)2,the following inequality can be obtained.

where
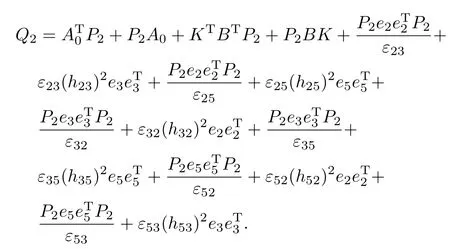
If the inequalityQ2<0 holds,it stands the time derivative of Lyapunov functionV2is negative,which means the system can be stabilized by the controller and the PMSMs′speed can follow the set point according to Lyapunov stability theory.Q2<0 can be written as(14)via Lemma 2.□
B.Robust Controller with Feedforward Compensation
In order to further reduce the conservative and the dependence on parameter of system,the control inputs can be divided into two parts,i.e.,
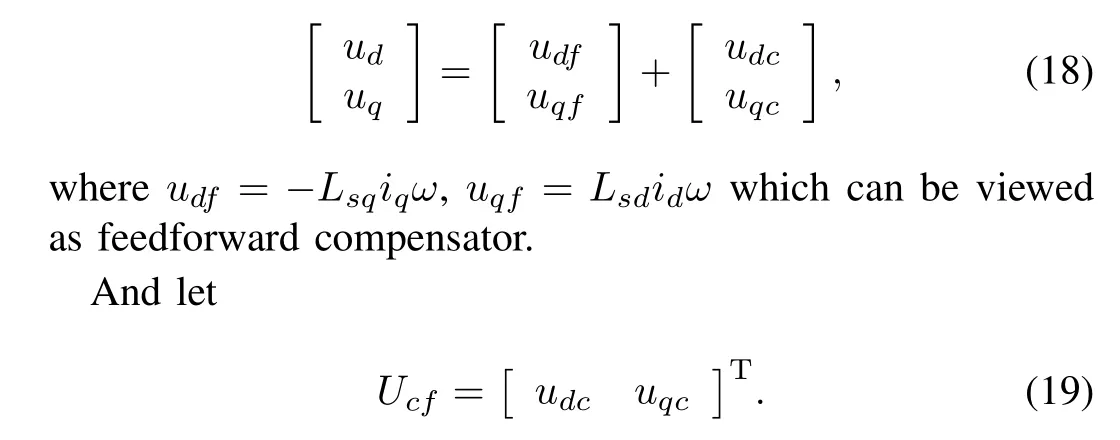
According to(3),(4),(18)and(19),the system can be described as
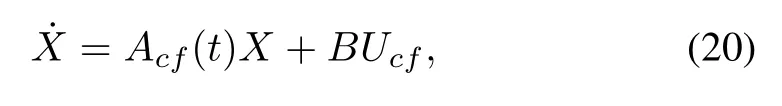
where

Condition(6)can be simpli fi ed as
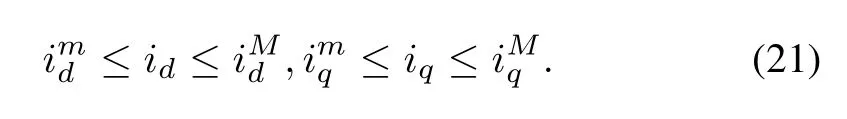
Similar to previous,Acf(t)can be rewritten as

where

The following theorem can be obtained.
Theorem 3.The PMSMs presented as(2)can be stabilized and the rotor angular speed can track the desired speed under the conditions(3)and(21)if there exist a symmetric and positive-de fi nite matrixPcf1∈R5×5,matrixKcf∈R2×5and positive scalarλsuch that the following BMI holds:
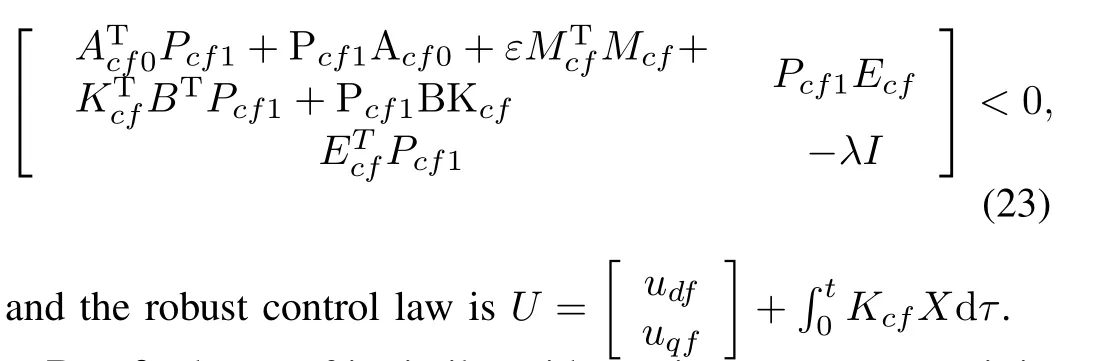
Proof.The proof is similar with previous.Here,we omit it.□
Similar to previous,Acf(t)can be rewritten as

The following theorem can be obtained.
Theorem 4.The PMSMs presented as(2)can be stabilized and the rotor angular speed can track the desired speed under the conditions(3)and(21)if there exist symmetric and positive-de fi nite matrixPcf2∈R5×5,matrixKcf∈R2×5,real scalarλ52>0 andλ53>0 such that the following BMI holds:

IV.SIMULATION
In this section simulations will be done to verify the effectiveness of proposed control methods by Matlab/Simulink soft.Referto[6],theparametersofthePMSMare given as:Prated=750W,ωrated=314rad/s,irated= 4.71A,Trated=2N·m,Lsd=0.004V,Lsq=0.004H,Rs=1.74Ω,ψr=0.1167Wb,np=4,Bf=7.403×10-5N·m·s/rad,andJ=1.74×10-4kg/m2.According to the parameter of PMSM,current and speed of the PMSM satisfy|id|≤30A,|iq|≤40A,|ω|≤350rad/s.The PWM switching frequency is 10KHz and the DC-link voltage is 300V.Solve inequality(8)with the help of Matlab soft,the following equations can be obtained.
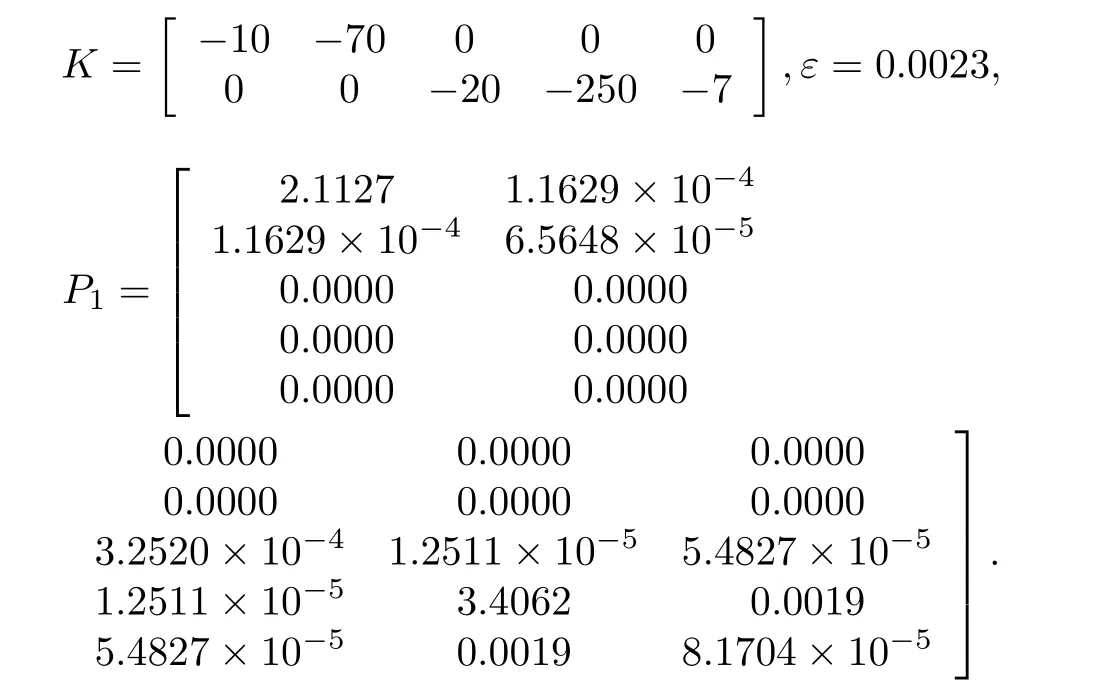
It means the motor can be stabilized and the rotator angular speed can track the desired speed if Theorem 1 is correct,and the robust control law(Method 1)are

If Theorem 3 is effective,the PMSM can be stabilized and the rotor angular speed can track the desired speed by the control law(proposed Method 2)which is described as follows.
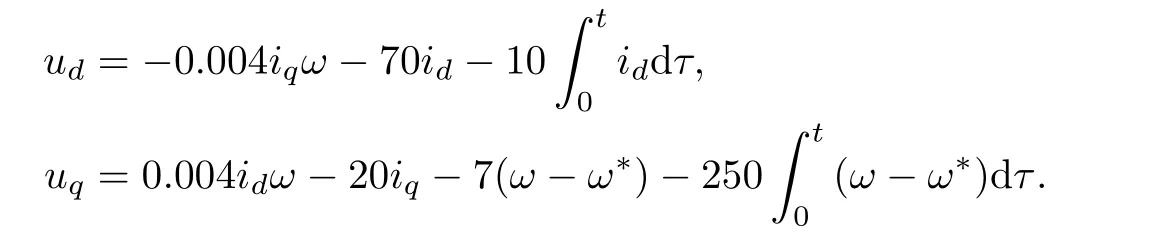
Next,simulations are carried out via Matlab/Simulink soft to demonstrate the judgment of Theorems 1 and 3.In thepractical application,the desired speed may be needed to change to satisfy the requirements and the load torque is often in fl uenced by the environment.Besides,the parameters of motor are also with time.For example,with the rise of temperature,the resistance value will increase.In order to comprehensive test the proposed controllers,three cases will be considered in the simulation.
Case 1.
1)The PMSM′s parameters are normal.
2)Thedesiredangularspeed:157rad/s→314rad/s(0.3s)→157rad/s(0.7s).
3)The load is constant and unknown.
Case 2.
1)The PMSM′s parameters are normal.
2)The desired angular speedω∗:314rad/s.
3)The initial load is constant and unknown,and the load suffer unit step disturbance in 0.4s and 0.7s.
Case 3.
1)The PMSM′s parameters change with time.
2)Thedesiredangularspeed:157rad/s→314rad/s(0.3s)→157rad/s(0.7s).
3)The load is constant and unknown.
The simulation results are depicted as Figs.1~6.It is obvious from these fi gures that the current and the speed all are in the given range,which mean the required conditions of the relevant theorems are satis fi ed.Figs.1~3 shows the simulation results of proposed method 1 under three cases. The simulation results of proposed Method 2 under three cases can be seen in Figs.4~6.In the fi gures,Δω=ω∗-ωstands the speed error;iaanduanare the phaseacurrent and the line to the neutral voltage,respectively.
Figs.1 and 4 show that the speed of PMSM can quickly track the desired speed and its change under the control of proposed Methods 1 and 2,respectively.These re fl ect the two methods have good tracking performance.it is obvious from Figs.2 and 5 that the proposed control Methods 1 and 2 can make the system effectively resist the load disturbance.Figs.3 and 4 re fl ect that although the parameters of PMSM change with time,the two proposed control methods can make the speed of motor track the desired speed,which comprehensively verify the control performance of the two methods. Comparing Figs.1~3 and Figs.4~6,we can conclude that the two control methods have similar control performance. Moreover,from these cases,we know that the load information is not needed in the two proposed controllers,which means the two proposed control strategies can deal with the load uncertainty.

Fig.1.The simulation results of proposed Method 1 under Case 1.
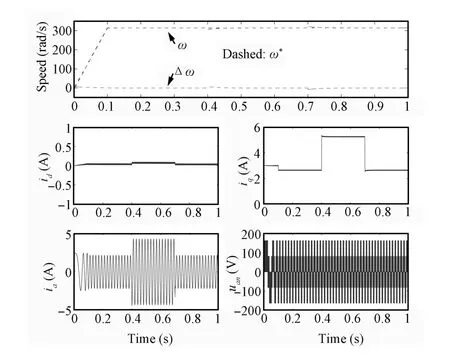
Fig.2.The simulation results of proposed Method 1 under Case 2.

Fig.3.The simulation results of proposed Method 1 under Case 3.
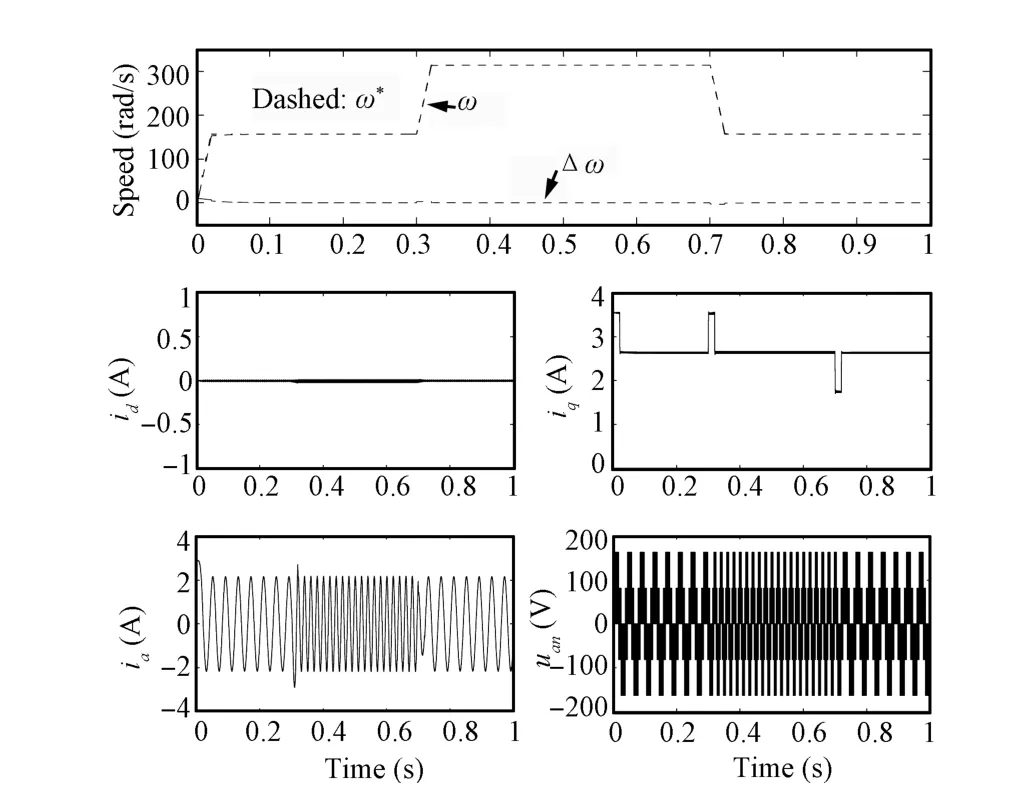
Fig.4.The simulation results of proposed Method 2 under Case 1.

Fig.5.The simulation results of proposed Method 2 under Case 2.
V.CONCLUSIONS
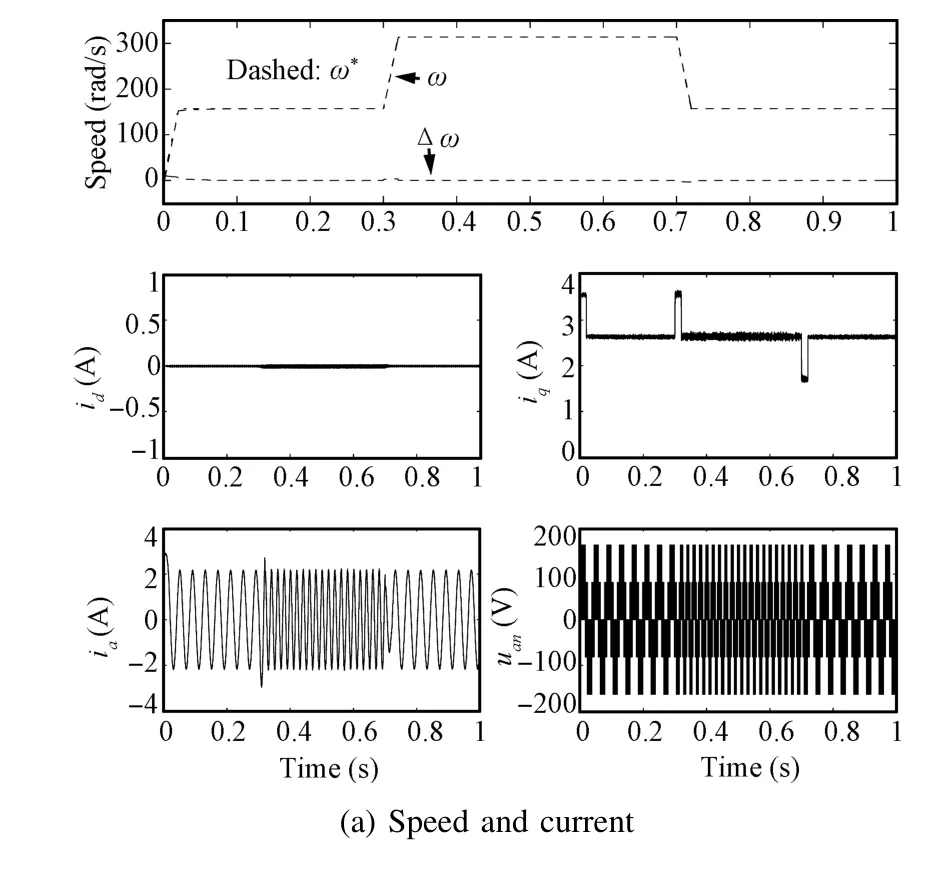
Fig.6The simulation results of proposed Method 2 under Case 3.
In this paper,a novel state equation of PMSMs has been obtained via the suitable choice of state variables.Based on the state equation,robust controllers of PMSMs have been developed via interval matrix and PI control idea.In terms of bilinear matrix inequations,suf fi cient conditions for the existence of the robust controllers have been derived.The proposed controllers can deal with load uncertainty and resist disturbances.In order to demonstrate the effectiveness of proposed control methods,computer simulations have been carried out via Matlab/Simulink.Simulation results have explained the proposed control methods have good control performance.
REFERENCES
[1]Yang S S,Zhong Y S.Robust speed tracking of permanent magnet synchronous motor servo systems by equivalent disturbance attenuation.IET Control Theory Applications,2007,1(3):595-603
[2]Corradini M L,Ippoliti G,Longhi S,Orlando G.A quasisliding mode approach for robust control and speed estimation of PM synchronous motors.IEEE Transactions on Industrial Electronics,2012, 59(2):1096-1104
[3]Choi H H,Vu N T T,Jung J W.Digital implementation of an adaptive speed regulator for a PMSM.IEEE Transactions on Power Electronics, 2011,26(1):3-8
[4]Underwood S J,Husain I.Online parameter estimation and adaptive control of permanent-magnet synchronous machines.IEEE Transactions on Industrial Electronics,2010,57(7):2345-2443
[5]Zhu H,Xiao X,Li Y D.Torque ripple reduction of the torque predictive control scheme for permanent-magnet synchronous motors.IEEE Transactions on Industrial Electronics,2012,59(2):871-877
[6]Liu H X,Li S H.Speed control for PMSM servo system using predictive functional control and extended state observer.IEEE Transactions on Industrial Electronics,2012,59(2):1171-1183
[7]Jin H Z,Lee J M.An RMRAC current regulator for permanentmagnet synchronous motor based on statistical model interpretation.IEEE Transactions on Industrial Electronics,2009,56(1):169-177
[8]Hamida M A,Leon J D,Glumineau A,Boisliveau R.An adaptive interconnected observer for sensorless control of PM synchronous motors with online parameter identi fi cation.IEEE Transactions on Industrial Electronics,2013,60(2):739-747
[9]Yue X,Vilathgamuwa D M,Tseng K J.Observer-based robust adaptive control of PMSM with initial rotor position uncertainty.IEEE Transactions on Industry Applications,2003,39(3):645-656
[10]Choi H H,Jung J W.Discrete-time fuzzy speed regulator design for PM synchronous motor.IEEE Transactions on Industrial Electronics,2013, 60(2):600-607
[11]Chaou H,Sicard P.Adaptive fuzzy logic control of permanent magnet synchronous machines with nonlinear friction.IEEE Transactions on Industrial Electronics,2012,59(2):1123-1133
[12]Leu V Q,Choi H H,Jung J W.Fuzzy sliding mode speed controller for PM synchronous motors with a load torque observer.IEEE Transactions on Power Electronics,2012,27(3):1530-1539
[13]Liu G H,Cheng L L,Zhao W X,Jiang Y,Qu L.Internal model control of permanent magnet synchronous motor using support vector machine generalized inverse.IEEE Transactions on Industrial Informatics,2013, 9(2):890-898
[14]Cheng B,Tesch T R.Torque feedforward control technique for permanent-magnet synchronous motors.IEEE Transactions on Industrial Electronics,2010,57(3):969-974
[15]Do T D,Choi H H,Jung J W.SDRE-based near optimal control system design for PM synchronous motor.IEEE Transactions on Industrial Electronics,2012,59(11):4063-4074
[16]Wai R J.Hybrid fuzzy neural-network control for nonlinear motor-toggle servomechanism.IEEE Transactions on Control Systems Technology, 2002,10(4):519-532
[17]Lu J G,Chen Y Q.Robust stability and stabilization of fractional-order interval systems with the fractional orderα:the 0≤α≤1 case.IEEE Transactions on Automatic Control,2010,55(1):152-158
[18]Guo L.H∞output feedback control for delay systems with nonlinear and parametric uncertainties.IEE Proceedings–Control Theory and Applications,2002,149(3):226-236
[19]Zhao L,Ham C,Han Q,Wu T X,Zheng L,Sundaram K,Kapat J, Chow L.Design of optimal digital controller for stable super-high-speed permanent-magnet synchronous motor.IEE Proceedings–Electric Power Applications,2006,153(2):213-218
[20]Chen B S,Yuan Y,Chen W,Ni G,Chen M.Electric Drive Automatic Control System:Motion Control System(Third Edition).Beijing,China: China Machine Press,2003(in Chinese)
[21]Khargonekar P,Petersen I,Zhou K M.Robust stabilization of uncertain linear systems:quadratic stabilizability andH∞control theory.IEEE Transactions on Automatic Control,1990,35(3):256-361
[22]Boyd S,Ghaoui L,Balakrishnan V.Linear Matrix Inequalities in System and Control Theory.Philadelphia,PA:SIAM,1994.
[23]Mao W J,Chu J.Quadratic stability and stabilization of dynamic interval systems.IEEE Transactions on Automatic Control,2003, 48(6):1007-1012

eng
the B.Sc.degree in Dalian Maritime University,Dalian,China and the M.Sc. degree in Central South University,China in 2011 and in 2014,respectively.His main research interests include control of electrical machines and distributed optimization.Corresponding author of this paper.

Manuscript received April 23,2014;accepted June 18,2014.This work was supported by National Natural Science Foundation of China(61075065, 60774045,61473314,U1134108),Ph.D.Programs Foundation of Ministry of Education of China(20110162110041),and Science Foundation of Innovation Research Groups of National Natural Science Foundation of China (61321003).Recommended by Associate Editor Zhiyong Geng.
:Zhenhua Deng,Xiaohong Nian.Robust control of permanent magnet synchronous motors.IEEE/CAA Journal of Automatica Sinica,2015, 2(2):143-150
Zhenhua Deng is with the School of Information Science and Engineering, Central South University,Changsha,410004,China,and also with the Key Lab of System and Control,Academy of Mathematics and System Science,Chinese Academy of Sciences,Beijing 100190,China(e-mail:@163.com).
Xiaohong Nian is with the School of Information Science and Engineering,Central South University,Changsha 410004,China(e-mail:xhnian@csu.edu.cn).
Xiaohong Nian received the B.Sc.degree,the M.Sc.degree,and the Ph.D.degree from Northwest Normal University,Shudong University and Peking University in 1985,1996,and 1999,respectively.He was a research fellow in the Institute of Zhuzhou Electric Locomotive from 2004 to 2008.Currently, he is a professor,the dean of the Faculty of Control Engineering of Central South University and an editor ofConverter Technology&Electric Traction. His research interests include coordinated control and optimization of complicated multi-agent system, converter technology and drive control,control of tractive power supply system in high-speed train.
杂志排行
IEEE/CAA Journal of Automatica Sinica的其它文章
- Single Image Fog Removal Based on Local Extrema
- An Overview of Research in Distributed Attitude Coordination Control
- Operation Ef fi ciency Optimisation Modelling and Application of Model Predictive Control
- Cloud Control Systems
- Stable Estimation of Horizontal Velocity for Planetary Lander with Motion Constraints
- Production Line Capacity Planning Concerning Uncertain Demands for a Class of Manufacturing Systems with Multiple Products
