一类变换半群的左相容元

2015-08-09薛琳,孙垒

信阳师范学院学报（自然科学版） 2015年4期

关键词：常值偏序反证法

薛琳 , 孙垒

(1.洛阳师范学院数学科学学院, 河南洛阳471002;2.河南理工大学数学与信息科学学院, 河南焦作 454003)

0 引言

Mitsch[1]在任意半群S上定义了如下偏序关系≤.

定理1[1]设≤是半群S上偏序关系,a,b∈S,则下面命题等价.

(i)a≤b.

(ii)a=wb=bz,az=a;w,z∈S1.

(iii)a=xb=by,xa=ay=a;x,y∈S1.

这种偏序关系通常称为半群S的自然偏序关系.

变换半群的自然偏序关系是变换半群理论中重要的研究课题,引起了国内外诸多学者的关注,参见文献[2-5]等.设TX是非空集合X(|X|≥3)上全变换半群,E是X上等价关系,X/E是等价关系E确定的X的分类(其中X/E的每个元素称为一个E-类),R是X/E的横断面(即X/E中每个E-类代表元的集合).文献[6]最早引入了TX的保持等价关系和横断面的子半群TE(X,R)={f∈TX:∀x,y∈X,(x,y)∈E⟹(f(x),f(y))∈E且f(R)⊆R},刻画了它的格林关系、正则元和富足性等.文献[7]赋予变换半群TE(X,R)自然偏序关系≤,即f,g∈TE(X,R),

f≤gf=kg=gh,f=kf,k∈TE(X,R),

描述了它的特征,得到了如下结论.

定理2[7]设f,g∈TE(X,R),则f≤g当且仅当下面条件同时成立.

(1)π(g)加细π(f).

(2) 若g(x)∈f(X)(其中x∈X),则f(x)=g(x).

(3) 对于任意A∈X/E,存在E-类B,使f(A)⊆g(B).

设h∈TE(X,R).若对于任意f≤g,有hf≤hg(fh≤gh),则h称为半群TE(X,R)的左(右)相容元.左(右)相容元是自然偏序关系≤的重要特性.文献[7]给出了半群TE(X,R)左相容元的充分条件,即:

定理3[7]设h∈TE(X,R).若h是X上单映射,则h是半群TE(X,R)的左相容元.

为弥补文献[7]的不足,本文以半群TE(X,R)为研究对象,在赋予半群TE(X,R)自然偏序关系的条件下,探寻刻画半群TE(X,R)左相容元的方法,通过构造合适的映射，给出左相容元的充要条件.

下面介绍本文中的概念和符号.π(f)表示由f∈TX确定的X的分类,即

π(f)={f-1(y):y∈f(X)}.

设f∈TE(X,R),记

E(f)={f-1(A):f-1(A)≠∅,A∈X/E}.

显然E(f)也是X的分类,且(f(x),f(y))∈E当且仅当x,y∈E(f).设A,B是集合X的两个子集族,若对于任意A∈A,存在B∈B,使A⊆B,则称子集族A加细子集族B.h|A表示映射h在集合A上的限制.本文等价关系E是非平凡的,即E≠X×X且E≠{(x,x):x∈X}.

1 几个引理

首先给出半群TE(X,R)左相容元的必要条件.

引理1[7]设f,g∈TE(X,R).若π(g)加细π(f),则E(g)加细E(f).

引理2 设h∈TE(X,R).若h是半群TE(X,R)的左相容元且|E(h)|>1,则E(h)=X/E.

证明反证法.若不然,不妨设U={A,B},其中U∈E(h);A,B∈X/E.由于|E(h)|>1,于是U⊂X.取定一点r∈R∪(X-U).定义映射f:X→X,

显然f∈TE(X,R)且f≤idX,其中idX是集合X上恒等映射.于是hf≤hidX=h.由定理2(1)知π(h)加细π(hf).根据引理1,有E(h)加细E(hf).但是,一方面,U∈E(h);另一方面,由r∉U,B⊂U知hf(U)=hf({A,B})=h(r)∪h(B)不包含在某一个E-类中.因此不存在V∈E(hf),使得U⊆V.这表明E(h)不加细E(hf).这与E(h)加细E(hf)矛盾，故E(h)=X/E.证毕.

引理3 设h∈TE(X,R).若h是半群TE(X,R)的左相容元,则对于任意E-类A,h|A是单射或者常值映射.

证明反证法.若不然,则存在E-类A*,满足h|A*既不是单射又不是常值映射.设h(a)=h(b)≠h(c),其中a,b,c∈A*.显然|{a,b}∩R|≤1.不失一般性,设a∉R,定义映射f:X→X，

则f∈TE(X,R)且f≤idX.于是hf≤hidX=h.由定理2(1)知π(h)加细π(hf).但是,一方面h(a)=h(b);另一方面,hf(a)=h(c),hf(b)=h(b).由h(c)≠h(b)知hf(a)≠hf(b).这与π(h)加细π(hf)矛盾.故命题成立.证毕.

2 主要结论

定理4 设h∈TE(X,R),则h是半群TE(X,R)的左相容元当且仅当下面两者之一成立.

(1) 若|E(h)|=1,则h是X上常值映射;或者,对于所有E-类A,h|A是单射且对于任意不同的B,C∈X/E,有h(B-R)∩h(C-R)=∅.

(2) 若|E(h)|>1,则E(h)=X/E且对于所有的E类A,h|A都是单射,或者对于所有的E类A,h|A都是常值映射.

证明必要性.设h是左相容元.由引理3知,对于任意E-类A,h|A是单射或者常值映射.现在用反证法证明不存在两个E-类A,B(|A|≥2,|B|≥2)满足h|A是单射且h|B是常值映射.若不然,设a∈A-R,A∩R={r1},B∩R={r2}.定义映射f:X→X,

显然f∈TE(X,R)且f≤idX.于是hf≤hidX=h.由定理2(1)知π(h)加细π(hf).但是,一方面h(r2)=h(b)(其中b是B中任意点，且b≠r2);另一方面,hf(r2)=h(r1),hf(b)=h(a).由h(r1)≠h(a)知hf(r2)≠hf(b).这与π(h)加细π(hf)矛盾.因此对于所有E-类A,h|A是单射或者常值映射.下面分两种情形进一步讨论.

情形1. |E(h)|=1.若对于所有的E类A,h|A都是常值映射,则h是X上常值映射.现在设对于所有E-类A,h|A都是单射.下面用反证法证明，对于任意不同B,C∈X/E,有h(B-R)∩h(C-R)=∅.若不然,即h(B-R)∩h(C-R)≠∅.令h(b)=h(c)=t,其中b∈B-R,c∈C-R.显然t∉R.令B∩R={r}.定义映射k:X→X,

则k∈TE(X,R)且k≤idX.于是hk≤hidX=h且π(h)加细π(hk).但是一方面h(b)=h(c);另一方面,hk(b)=h(b)=t∉R,hk(c)=h(r)∈R.由t≠h(r)知hk(b)≠hk(c).这与π(h)加细π(hk)矛盾.

情形2. |E(h)|>1.由引理2知E(h)=X/E.故必要性成立.

充分性.设f,g∈TE(X,R)且f≤g.显然对于任意h∈TE(X,R),hf和hg满足定理2(3).下面分两种情形验证hf,hg满足定理2(1-2).

情形1. |E(h)|=1,则|h(R)|=1.若h是常值映射,则h是左相容元.现在设h不是常值映射.此时,由题设知对于所有E-类A,h|A是单射且对于任意不同的B,C∈X/E,有h(B-R)∩h(C-R)=∅.

(1) 设hg(x)=hg(y),其中x,y∈X.此时有两种可能.

(P1).g(x)=g(y).根据f≤g和定理2(1),有f(x)=f(y),即hf(x)=hf(y).

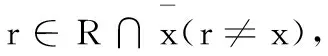
(2)设hg(x)∈hf(X),即hg(x)=hf(x′),其中x′∈X.此时有两种可能.

(P1)’.g(x)=f(x′),则f(x)=g(x),即hf(x)=hg(x).

(P2)’.g(x)≠f(x′).如(P2)所证,有g(x),f(x′)∈R且f(x)∈R.因此hf(x)=hg(x).这表明hf,hg满足定理2(2).

情形2. |E(h)|>1.此时E(h)=X/E.

(1)设hg(x)=hg(y),其中x,y∈X.此时有两种可能.

(P1).g(x)=g(y).于是f(x)=f(y),即hf(x)=hf(y).

(P2).g(x)≠g(y),则(g(x),g(y))∈E且h在每个E类A上都是常值映射.于是(f(x),f(y))∈E,即hf(x)=hf(y).这表明hf,hg满足定理2(1).

(2)设hg(x)∈hf(X),即hg(x)=hf(x′),其中x′∈X.此时有两种可能.

(P1)’.g(x)=f(x′).于是f(x)=g(x),即hf(x)=hg(x).

(P2)’.g(x)≠f(x′),则(g(x),f(x′))∈E.设f(x′)=g(y),其中y∈X.由定理2(2)知f(y)=g(y)=f(x′).进而(g(x),g(y))∈E.因此(f(x),f(y))∈E,即(f(x),f(x′))∈E.由等价关系E对元素的传递性知(f(x),g(x))∈E.当然有hf(x)=hg(x).这表明hf,hg满足定理2(2).

因此无论何种情形,hf,hg都满足定理2(1-2),从而hf≤hg,即h是半群TE(X,R)的左相容元.故充分性成立.证毕.