基于模糊均值的细菌群体趋药性复杂网络社团结构发现

李艳灵，刘先省

(1.河南大学 环境规划学院， 河南 开封 475004;2.信阳师范学院 计算机与信息技术学院, 河南 信阳 464000)

0 引言

近年来，对复杂网络性能的研究与理解，特别是对交通运输网、社交网络、万维网、论文引用网络的研究与理解日益重要[1-3].复杂网络的重要特征之一是社团结构.同一社团内部节点之间联系紧密，不同社团之间节点联系稀疏.由于社团结构影响着组织的重要功能，因此社团结构发现非常重要.例如,论文引用网络按照相似的研究课题分类;社会网络按照兴趣爱好、职业进行分类.因此网络中的社团发现能力对于实际应用具有重要的影响，并有助于我们理解网络系统.

尽管网络社团结构的概念非常简单，但是构造有效的社团结构发现算法却十分困难.为此，研究者们提出了一系列的算法[4-6]，取得了一定的效果.但是，目前大多数算法将复杂网络中的关系确定化，这种方法强调网络中的节点确定的隶属于一个社团.但是现实世界中，网络中的节点可以同时隶属于不同的社团.因此本文提出基于模糊均值的细菌群体趋药性复杂网络社团结构发现算法.首先利用细菌群体趋药性算法获得模糊均值算法的初值，然后利用模糊C均值算法进行社团结构发现.最后通过实验验证文章所提算法的有效性.

1 细菌群体趋药性算法

细菌趋药性算法[7](Bacterial chemotaxis, BC)是新近提出的一种随机梯度优化算法.该算法只依赖于单个细菌的运动行为，通过不断地感受其周围环境的变化和只利用其过去的经验寻找最优点.BC算法把单个细菌当作是一个受其周围环境影响而改变位置的个体，并且利用感知的信息改变细菌的移动轨迹，并且在移动过程中不断修正前进的角度和移动的距离，以找到目标函数的最优值.算法步骤如下：

(1)计算细菌的移动速度，假设其为常数；

v=const.

(1)

(2)计算细菌在新方向上的移动时间τ，τ的值由概率分布决定：

其中T由下式决定：

其中T0是最小平均移动时间，fpr为当前点与上一个点之间的函数值的差，lpr为变量空间中连接当前点和上一个点的向量的模，b是与参数无关的参数.

(3)计算新的运动方向.原来轨迹和新方向之间的夹角根据新方向向左或向右偏转分别服从以下两个高斯概率分布：

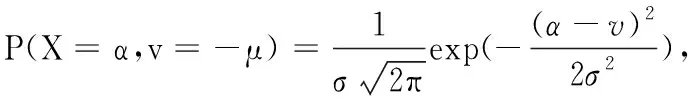
其中，其方差和期望分别由下式决定：当fpr/lpr<0时，

σ=260(1-cosθ),

(5)

μ=620(1-cosθ),

(6)

cosθ=e-τcτpr,

(7)

其中:τc为相关时间，τpr为细菌上一运动轨迹的持续时间.

(4)计算细菌在变量空间中的新位置：

上述算法中，T0,b,τc,v是需要设定的系统参数.优化过程中对参数的自适应调整可以加速寻优的过程.

BC算法作为一种随机梯度搜索方法，具有一定的避免算法陷入局部优化的能力，并且该算法能够防止算法过早收敛.然而，由于BC算法不是基于群体智能的优化算法，它只依赖于单个细菌的运动行为，不断感受其周围环境的改变，并且只利用它过去的经验来寻找最优值，因此该算法有如下的缺陷:第一，单个细菌必须在解空间中通过搜索不同的点以修正和模拟其形成的梯度信息，因此，在很多问题上，BC算法的优化速度慢;第二，当函数的梯度变化小于一定的值时，细菌个体将无法得到合适的梯度信息，从而进入随机搜索.随着精度的提高，BC算法的搜索范围将很难保证限定在全局最优解的附近.为此，我们提出细菌群体趋药性算法(Bacterial colony chemotaxis, BCC).该算法引入精英保持策略，该策略保证了BCC的执行效率，并且避免丢弃那些具有较好位置的点.经过若干步后，具有较差位置的节点向较好位置的点移动.公式如下：

其中，rand()是(0,2)内的正态分布.

2 基于模糊均值的细菌群体趋药性复杂网络社团结构发现算法

2.1 相似性度量方法

文献[8]中，定义了节点之间的非类同指数，该指数用于网络中节点之间接近程度的度量.复杂网络可以表示成图G(S,E)，其中S是节点的集合,E={e(x,y)}x,y∈S为带权矩阵，e(x,y)为连接节点x和y的边的权值.将复杂网络描述成含随机矩阵P=(p(x,y))的离散马尔科夫链如下：

其中d(x)为节点的度.非类同指数定义为：

其中|Sk|为社团中的节点个数.

2.2 基于模糊均值的细菌群体趋药性社团结构发现算法

复杂网络中的社团内部节点之间联系稠密，社团之间节点联系稀疏.社团结构发现就是为了揭示不同类型复杂网络中存在的真实社团结构.为了定量地刻画社团发现算法，2004年Newman等[9]提出了网络模块性评价函数——模块度(Q)，其定义如下：

3 实验结果分析

为验证本文所提算法的有效性，将该算法用于简单网络和Zachary空手道俱乐部网络.图1(取自文献[10])为具有明显3个社团结构的简单网络，网络中包含19个节点.

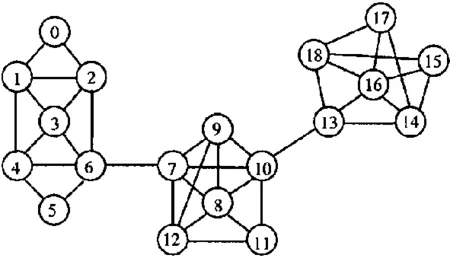
图1 三社团网络Fig. 1 Network with three communities

应用本文算法对该简单网络进行社团划分，分别得到聚类数k={1,2,3,4,5,6}对应的模块度值Q={0,0.159,0.574,0.441,0.344,0.335}.可知当网络被划分三个社团时，对应的模块度值Q达到最大，因此，网络的最优社团划分是聚类数k=3所对应的社团划分结果.

图2是著名的Zachary空手道俱乐部网络最终的划分结果.该俱乐部的主管与校长之间因是否提高俱乐部收费的问题产生了争执.结果，该俱乐部分裂成了两个分别以主管和校长为核心的小俱乐部.图2中方形节点与圆形节点代表实际分裂而成的两个小俱乐部，而阴影和非阴影代表应用本文算法得到社团划分结果.

图3给出了不同聚类数k下相应的模块度值Q，可知Zachary空手道俱乐部网络被划分成两个社团为最终的社团划分结果.可见本文算法具有更高的准确率，而且把有歧义的3号节点同样正确划分.

图2 Zachary空手道俱乐部网络Fig. 2 Zachary’s karate club network

图3 网络划分为k个社团时所对应的模块度值Fig. 3 Modularity of network with k community structures

4 结语

本文提出基于模糊均值的细菌群体趋药性算法用于复杂网络的社团发现.该算法解决了复杂网络社团发现中的模糊性和不确定性问题.新算法中，无须关于社团结构的先验知识即可有效地确定最优的社团个数和每个社团的中心点.如何将模糊聚类和其他群体智能算法进行结合，并用于探测复杂网络的社团结构是值得进一步研究的课题.