未知外部荷载下结构的在线损伤诊断

林秋爽，周 欢，刘锦涛

(1. 信阳师范学院 土木工程学院, 河南 信阳 464000；2. 厦门大学 建筑与土木工程学院， 福建 厦门 361000)

0 引言

结构损伤诊断是当前土木工程界十分活跃的研究领域,结构的在线损伤诊断是其中一个重要方面，其对保障人民的人身和财产安全具有重大意义，研究土木工程结构的在线损伤识别技术极为重要.

近年来，很多专家学者致力于研究时变系统参数识别问题和实时损伤诊断技术.Chu 和 Lo[1]提出基于自适应参考模型的识别技术.Yang 和Huang[2-4]提出各种自适应损伤追踪算法，用自适应遗忘因子矩阵代替标量的时变遗忘因子用来实时追踪结构参数由于老化或损伤导致的变化.然而应用自适应遗忘因子矩阵的数学推导和计算量很大.Lu[5]等和Huang等[6]提出了采用时间序列分析算法.杜永峰等[7]针对如何从结构响应信息中提取结构损伤指标的问题,也提出了一种基于时间序列分析的结构损伤识别方法，对结构损伤进行识别.董君等[8]提出一种基于自回归支持向量机的结构损伤诊断算法.尹强[9]等提出基于ASNLSE方法的橡胶隔震结构损伤识别方法.

上述各种结构实时损伤追踪方法还存在局限性，如公式推导复杂，计算量大，需对结构的动力响应和外部激励全观测等.针对时变系统，本文基于扩展卡尔曼预测估计和最小二乘估计算法提出未知荷载下结构在线损伤识别算法，在输入输出信息不完备的情况下仍能准确地识别结构参数并追踪其变化，同时识别未知外部荷载.

1 未知荷载下在线损伤诊断算法

在已知和未知外部荷载作用下，多自由度体系的动力方程可写为如下形式:

Bf(t)+Bufu(t),

(1)

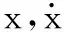
1.1 第一阶段

方程关于增广状态向量的方程可写为：

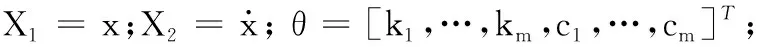
a2=M-1(Bf(t)+Bufu(t)-

ki,ci为刚度和阻尼系数;w(t)为模型误差，假定均值为零，协方差矩阵为Q(t).

将上式写成一般的非线性状态向量微分方程：

补充结构的观测方程：

Gu=DM-1Bu,

h(Xk,fk,tk)=

根据扩展的卡尔曼预测估计，有状态预测方程：

状态估计方程：

其中Kk为最优增益矩阵[10].

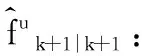
其中R为观测噪声v的协方差矩阵.

1.2 第二阶段

待识别的结构参数在第一阶段的识别过程中逐渐收敛并稳定后,即进入第二阶段.在该算法中，在此阶段判断结构刚度参数突变发生的时间与可能损伤单元的位置，判断是基于在局部损伤单元及其附近部位的加速度信号会在突然损伤后立即出现偏差.

对于一个多层剪切框架结构，如果第i层刚度突变，会立即影响到第i-1层和第i层的观测加速度信号.即当第i层突然发生损伤,则第i-1层和第i层的加速度响应信号会立刻出现偏差，而其他层则会在一段时间之后受到较明显的影响.换句话说，离损伤层越远的楼层，其受到的影响越小,也越晚.

在(k+1)Δt时刻，定义第i个加速度传感器观测的加速度与预测加速度间的误差为

其中yi,k+1表示(k+1)Δt时刻第i个传感器观测的加速度值.

定义(k+1)Δt时刻观测加速度和预测加速度值间的误差的平方和为：

其中d表示加速度传感器的数量.

因为加速度的预测值是在假设结构为时不变系统的前提下得到的，Δk+1的突然增大即意味着结构刚度在(k+1)Δt时刻发生突变.

1.3 第三阶段

优化函数的目标函数为以下形式，

其中j=1,2,…,p，表示与第i个自由度相关的可能发生损伤的单元;p为可能发生损伤的单元的数量.

约束函数的表达式如下:

2 数值算例

本节以八层平面剪切框架为例验证本文所提出的结构在线损伤诊断技术的准确性和稳定性.该平面框架的各层质量，刚度和阻尼分别为：m1=m2=…=m8=60 kg,k1=k2=…=k8=1.2×105N/m,c1=c2=…=c8=200 N/m.

该算例中，结构的顶部受到均值为零的白噪声激励的作用(如图1).其中1、3、5、7、8层放置加速度传感器;第2、4、6层加速度不观测，且加速度信号受到5%的噪声污染.在t=2.5 s时第一层和第五层同时发生损伤，刚度由原始数值分别降低为k1=k3=0.6×105N/m，其他参数不变.

图1 八层平面剪切框架Fig. 1 Eight stories shearing frame

结构采用集中质量，质量矩阵M为对角矩阵.整体刚度矩阵如下，阻尼矩阵同理.

由于观测得到的加速度信号会受到噪声的污染，因此若在识别外部荷载作用的同时识别系统参数和结构响应，则会出现位移和未知荷载识别图与实际值趋势相同，但是图形整体向上或向下飘移的现象，会影响到此刻刚度突变值的优化.因此，这里采用最小二乘法消除趋势，可用Matlab中的函数Polyfit使得飘移的识别值逼近真实值.采用此方法消除未知力飘移趋势后的力识别值与荷载的实际值吻合得很好.在得到kΔt时刻较准确的未知荷载的估计值后，可利用该时刻的速度估计值和结构参数估计值，代入此刻的动力方程中求出每个自由度在kΔt时刻的位移响应值.得到kΔt时刻较准确的系统动力响应，结构参数和未知外部激励的估计值后，再进行(k+1)Δt时刻刚度突变值的优化.

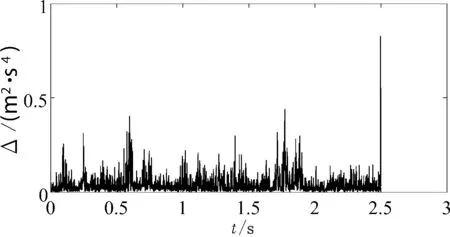
图2 预测加速度与观测加速度的误差平方和Fig. 2 Sum of squares of errors between estimated and observed accelerations

在算例中，首先通过卡尔曼预测估计得出结构损伤前的刚度、阻尼、速度、位移和外部荷载的估计值；待到识别过程稳定，2.5 s处结构出现损伤，即第一、五层的刚度发生突变，此刻预测加速度与观测加速度的误差平方和突然增大，如图2所示，2.5 s处误差平方和明显变大，且其中一、五层的预测加速度与观测加速度的误差的平方值最大(如图3)，即诊断出损伤发生的时间且位置在一、五层.

图3 损伤时刻各层预测加速度与观测加速度的误差的平方Fig. 3 Square of error between estimated and observed accelerations of each floor in damage moment

接着，采用MATLAB中的优化函数计算刚度突变值.给出结构刚度突变的范围Δk=0～1.2×105N/m，此函数通过代入给出范围内不同的突变值进行大量反复迭代试算，最终达到将目标函数值——预测加速度与观测加速度的误差平方和降到最小的目的，使目标函数值取值最小的刚度突变值为最优，即为所求.

从数值模拟的计算结果图看，图4表明刚度的损伤识别可以很快并且较准确地收敛到真实值，在2.5 s处，一、五层刚度的突变能够被该算法准确地追踪到，且2.5 s之后刚度的损伤识别依然较准确.图5中未知荷载的识别结果为用最小二乘法消除趋势后的结果，结果清楚地表明用该算法计算得到的未知荷载与荷载的真实值比较吻合.从图2和图3可以看出该算法可以很精确地判断出突变发生的时间是在2.5 s处，突变位置在结构的第一、五层.用本文提出的追踪方法可以较准确地在发生突变地时刻诊断出损伤程度.

图4 第一、五层刚度参数识别和损伤诊断Fig. 4 Identification of stiffness and damage detection of the 1st and 5th story

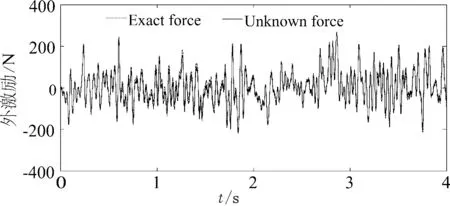
图5外部激励的识别

Fig. 5Identificationofexternalloading

3 结论

本文提出一种未知荷载下的结构损伤诊断在线追踪技术来识别结构的物理参数及追踪其变化，尤其是由于结构损伤而导致的结构刚度系数突变.该算法的创新点在于其思想直观易懂，公式推导简单明了，物理意义明确，且计算简便，算法可以很快收敛并稳定，只需要部分观测加速度响应信号.不仅如此，这种算法考虑了结构外部荷载未知的情况.由于在实际工程中结构外部荷载通常是未知的，本算法可以在实时追踪时变系统的损伤同时，在线识别未知的外部荷载.数值算例的结果表明，本文提出的算法尤其适用于解决未知荷载作用下线性结构由损伤导致的参数突变.而且，这种损伤追踪技术对噪声影响不敏感，具有较好的抗噪能力.

然而本文提出的算法仍存在一些限制条件.算法在结构参数的识别收敛并稳定之后才能进行损伤诊断；如果观测的加速度信号受到噪声污染，则该算法无法识别刚度的微小损伤；且在一个损伤单元中，至少有一个加速度信号被观测，否则无法追踪单元损伤发生的时刻.通常情况下，第一个限制条件不会给损伤诊断造成困扰，因为扩展卡尔曼预测算法一般会很快收敛并稳定.对于第二个限制条件，通常在结构损伤诊断算法中都会存在这个问题.由于该算法是通过结构加速度响应的变化来判断损伤发生的时刻，所以这个方法目前对于结构发生渐变的情况还不能应用.由于第三个限制条件的影响，尽管该算法可以采用加速度信号部分观测，但是对于剪切框架来说，加速度传感器必须隔层放置.另外本文只针对剪切框架进行了研究，针对更复杂的建筑结构以及结构发生渐变损伤的情况还有待以后继续研究.