基于敏感传递函数的分数阶PIλ 控制器的参数整定

（天津科技大学电子信息与自动化学院，天津 300222）

（天津科技大学电子信息与自动化学院，天津 300222）

讨论一种基于敏感传递函数的分数阶PIλ控制器的参数整定方法.根据敏感传递函数的定义，采用代数方法，对固定的PIλ控制器的积分阶次，在比例增益和积分增益参数平面上，按敏感传递函数的界进行PIλ控制器的参数整定.该敏感传递函数的界与系统的幅值裕度和相角裕度直接相关，给出了系统相对稳定性的信息.仿真实例表明，利用该方法设计的PIλ控制器具有良好的动态性能和鲁棒性.

分数阶PIλ控制器；敏感传递函数；参数整定

分数阶控制系统的相关研究近年来受到广泛的关注［1-2］，特别是分数阶PID控制器的研究［3-5］具有明显的工程实际意义.众所周知，常规（整数阶）PID控制器在工业过程控制领域获得了广泛应用.采用分数阶PID控制器，由于增加了设计的自由度，可以取得比整数阶PID更好的动态性能和对参数变化的鲁棒性.幅值裕度和相角裕度作为相对稳定性的度量，在经典控制理论中已进行了大量的讨论.相角裕度与时域动态性能（超调量）直接相关，而幅值裕度则反映系统对参数变化的鲁棒性.

本文讨论基于敏感传递函数的分数阶PIλ控制器的参数整定方法.该敏感传递函数的界给出了幅值裕度和相角裕度的信息.通过一种代数方法求解PIλ控制器的参数，并用仿真实例进行验证.

1 敏感传递函数

考虑图 1所示SISO单位反馈系统，其中 G（s）为被控对象，C （s）为控制器，R （s）为参考输入，Y（s）为输出，E （s）为跟踪误差.敏感传递函数 S（s）定义为

它代表系统对参考输入信号的跟踪精度.考虑频率特性 （j）Sω的最大值

其物理意义是，开环 Nyquist曲线到系统临界稳定点（-1，j0）的最短距离的倒数，典型取值范围为（1，2）［6］.进一步，文献［7］将式（2）的极大化问题转换为在整个频率范围内对敏感传递函数进行约束

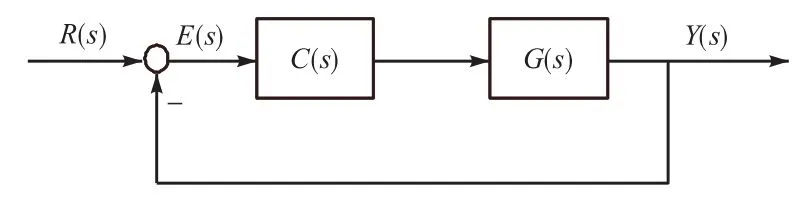
图1 单位反馈系统Fig. 1 Unity feedback system

式中 1M＞ .根据这一条件，当M→∞时，式（3）成为闭环特征方程

事实上，式（3）的敏感传递函数不等式约束与系统的幅值裕度和相角裕度直接相关［7］：

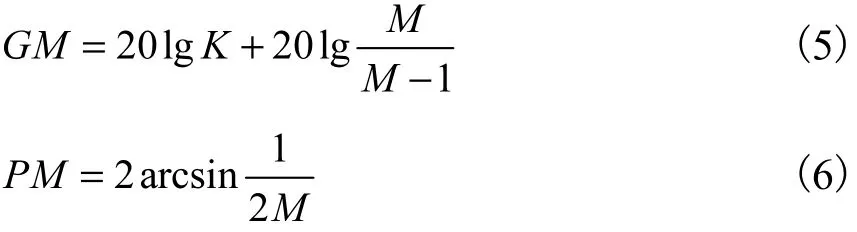
式中 1K≥ 为系统的开环增益.因此，式（3）不等式是对系统鲁棒性的一种比幅值裕度和相角裕度更强的度量，因为它不只是在 2个穿越频率（相角穿越频率和幅值穿越频率）处对敏感传递函数进行界定，而是在所有频率处对其进行约束.

2 控制器参数整定

设图1中被控对象的传递函数为?

式中：D （s）和 N（s）为整数阶或分数阶多项式；L ≥0为时滞因子.控制器为如下分数阶PIλ形式

式中：pk和ik分别为比例增益和积分增益；0 2λ＜ ＜为积分阶次.为设计方便，对式（8）的控制器进行如下变换

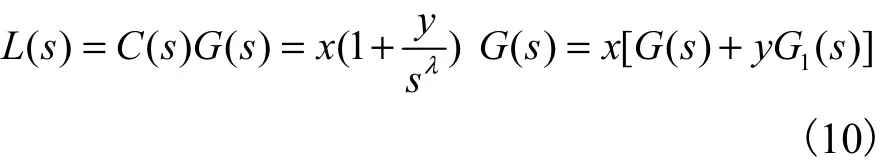
代入式（10），有

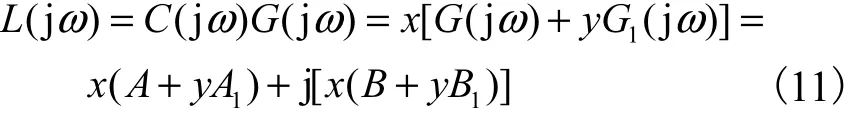
由式（3）可得

定义函数

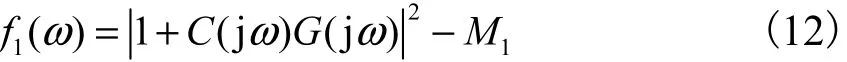
.再由式（11），f1（ω）可写为

其中

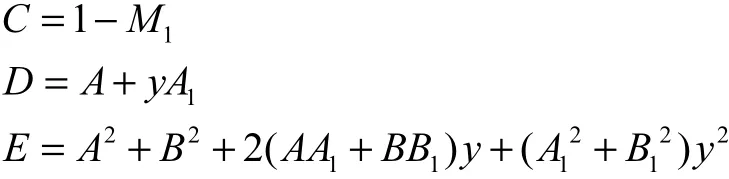
式（13）定义了一个极值问题，当在某一频率下，等号成立时，1（）fω达到极小值.由极值条件可得

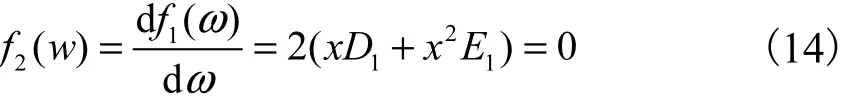
其中

联立求解方程组

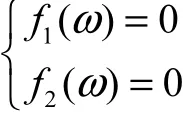
消去2x后，得到

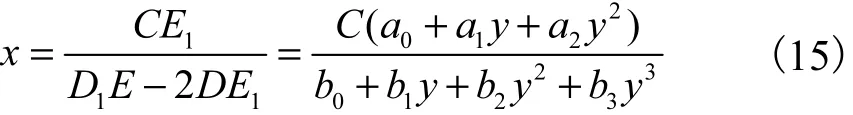
其中

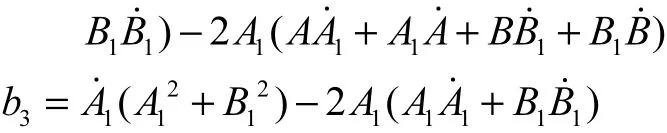
将式（15）代入式（13）中的 f1（ω）= 0，整理得关于参数y的6次方程

其中

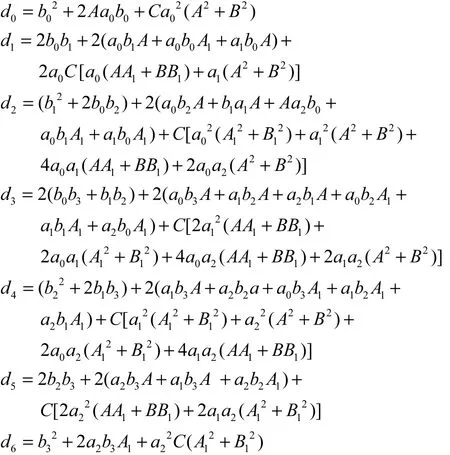
可按如下方法求解参数对（x，y）：在适当选取的频率ω下，解关于y的6次方程（16），得出6个解，分别代入式（15），得相应的x.然后，根据参数变换公式kp= x，ki= xy解得参数对 （kp，ki）.所需要的解应该是落在参数稳定域（令M→∞可得）内的实数解.对适当选取的频率范围，参数对（kp（ω） ，ki（ω））在稳定域内描绘出一条满足敏感传递函数界 M＞1的曲线.

3 仿真实例

考虑单容水箱传递函数［9］

在图 1所示控制系统中，采用式（8）给定的分数阶PIλ控制器，文献［8］讨论了PIλ控制器分数阶次λ与（kp，ki）平面上参数稳定域的面积大小之间的关系，结论是λ越小，稳定域面积越大.选取 λ= 0.2，根据前两节的讨论，选取足够大的M值，可得（kp，ki）平面上的参数稳定域，如图2中的虚线所示.再分别取 M=8和 M= 1.46，落在稳定域内的实数解描绘出的曲线分别如图 2中两条实线所示.根据式（5）和式（6），M = 1.46对应的相角裕度约为 40°，幅值裕度约为11，dB.沿 M= 1.46的曲线取点A（见图3），再在曲线内部取点 B，分别作阶跃响应，如图 4所示.由于B点对应的相角裕度大，相应的阶跃响应的超调小.另外，由于控制器的积分阶次较小（ λ= 0.2），阶跃响应存在一定的稳态误差，可以采用其他方法进行补偿.

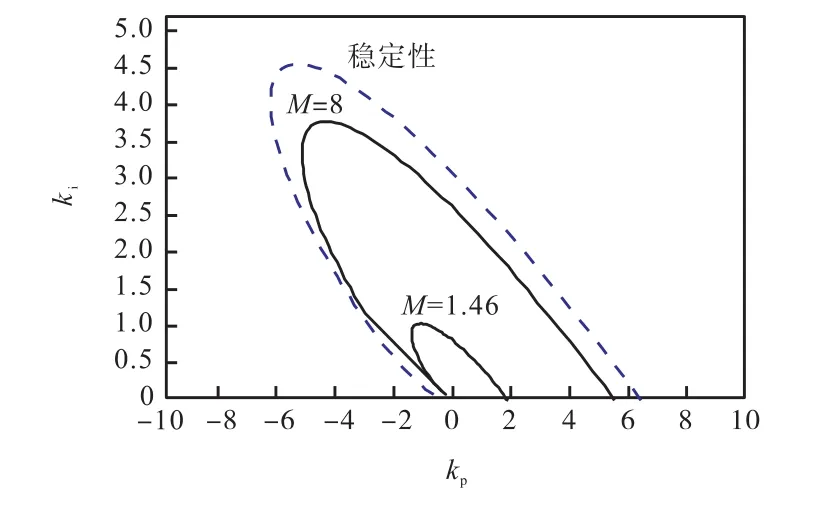
图2 不同M对应的敏感约束Fig. 2 Sensitivity constraint for different M

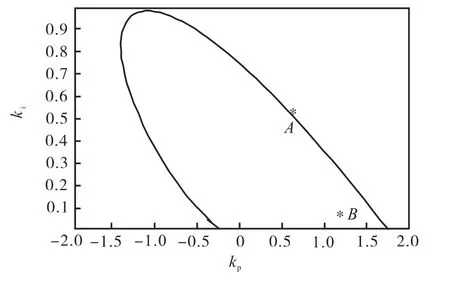
图3 M=1.46对应的敏感约束Fig. 3 Sensitivity constraint for M=1.46

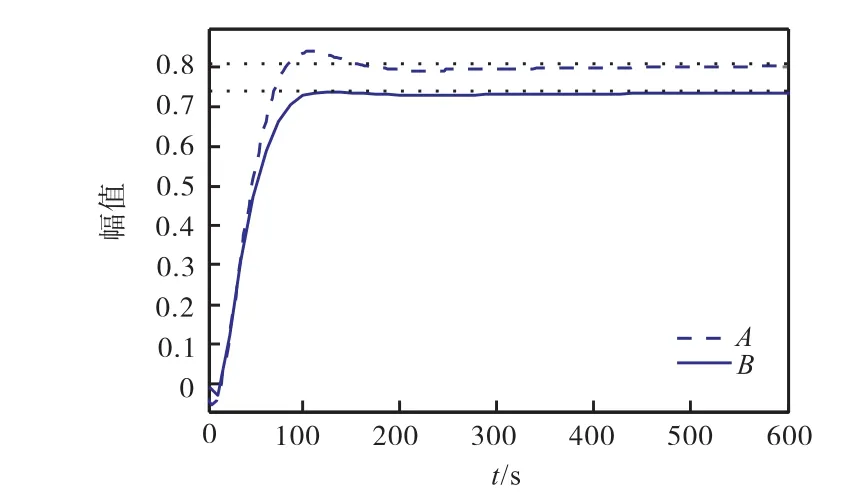
图4 A、B 两点对应的阶跃响应Fig. 4 Step responses corresponding to A and B

4 结 语

本文给出了一种分数阶PIλ控制器的图解参数整定方法，即基于敏感传递函数界的参数整定方法.该方法的特点是控制器的参数选择灵活，所设计的控制器能同时满足相角裕度和幅值裕度的要求，可以直接应用于过程控制领域.

［1］ Podlubny I. Fractional Differential Equations［M］. San Diego：Academic Press，1999.

［2］ 薛定宇，赵春娜. 分数阶系统的分数阶 PID控制器设计［J］. 控制理论与应用，2007，24（5）：771-776.

［3］ Podlubny I. Fractional-order systems and PIDλμcontrollers［J］. IEEE Transactions on Automatic Control，1999，44（1）：208-214.

［4］ Hamamci S E. An algorithm for stabilization of fractional order time-delay systems using fractional order PID controllers［J］. IEEE Transactions on Automatic Control，2007，52（10）：1964-1969.

［5］ Lou Y，Chen Y Q，Wang C Y，et al. Tuning fractional order proportional integral controllers for fractional order systems［J］. Journal of Process Control，2010，20（7）：823-832.

［6］ Astrom K J，Panagopoulas H，Hagglund T. Design of PI controllers based on non-convex optimization［J］. Automatica，1998，34（5）：585-601.

［7］ Yaniv O，Nagurka M. Design of PID controllers satisfying gain margin and sensitivity constraints on a set of plants［J］. Automatica，2004，40（1）：111-116.

［8］ Wang D，Zhang J. A graphical tuning of PIλcontrollers for fractional order systems［J］. Journal of Control Theory and Applications，2011，9（4）：599-603.

［9］ 蔡国娟. 液位控制系统分数阶PIλ控制器设计及实验［D］. 天津：天津科技大学，2012.

基于敏感传递函数的分数阶PIλ控制器的参数整定

杨征颖，王德进，史万祺

Parameter Tuning of Fractional-order PIλControllers Based on Sensitivity Constraint

YANG Zhengying，WANG Dejin，SHI Wanqi
（College of Electronic Information and Automation，Tianjin University of Science & Technology，Tianjin 300222，China）

This paper discusses the parameter tuning method of fractional-order PIλcontrollers based on sensitivity transfer function constraint.According to the definition of sensitivity transfer function，in the plane of proportional-integral gains of PIλcontroller，for fixed integral-order，the parameters of the controller are tuned by plotting the sensitivity bound obtained via an algebraic derivation. The bound of sensitivity transfer function is directly related to the gain-margin and the phase-margin of the system，which gives the information on the relative stability of the system. Simulation examplesprove that the designed PIλcontroller can achieve better dynamic performances and robustness.

fractional-order PIλcontrollers；sensitivity transfer functions；parameter tuning

TP273 文献标志码：A 文章编号：1672-6510（2015）02-0057-03

10.13364/j.issn.1672-6510.20140106

2014-07-11；

2014-09-17

国家自然科学基金资助项目（60874028）

杨征颖（1988—），女，河北廊坊人，硕士研究生；通信作者：王德进，教授，wdejin56@sina.com.

常涛