图的给定匹配数的离心率距离和
2015-08-09天津科技大学理学院天津300457
(天津科技大学理学院,天津 300457)
(天津科技大学理学院,天津 300457)
针对可预测生物和物理性质的图的不变量——离心率距离和,采用Tutte-Berge公式及图的转化方法,给出了图的给定匹配数的离心率距离和的紧下界,且完全确定了其极值图.
离心率距离和;匹配数;极值图
Wiener指标定义为对所有无序顶点对之间距离的求和[1]:
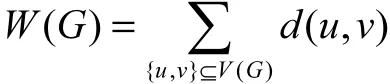
它被认为是与分子化合物的许多物理和化学指标高度相关的最有用的拓扑指标之一.
1997年,Sharma等[2]引进了 1个基于距离的分子结构描述量,被称为离心率连通性指标(ECI),定义为ξc(G)指标被成功应用在不同性质的生物活性的数学模型上[2].

2002年,Gupta等[3]提出了1个新奇的预测生物和物理性质的图的不变量——离心率距离和.他们证明了对一些构造活动和定量结构性质的研究,使用离心率距离和所得的值比使用 Wiener指标要好.离心率距离和(EDS)定义为


如果图的1个连通分支含有偶(或奇)数个顶点,那么称这个连通分支是偶(或奇)的.令G是1个有n个顶点的图,且 o(G)表示G中奇分支的个数.由Tutte-Berge公式[4],有

图G和H的顶点不交的并,记作G H∪ .令G H∨ 表示在G H∪ 中通过从G中的顶点向H中的顶点连接所有可能的边而所得的图,即
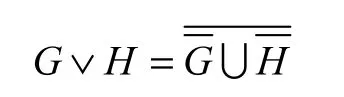
因为在图中添加新边会降低一些距离,所以有:

Feng等[5]研究了在阶为n且匹配数是β的所有图中有最大谱半径的极值图.Zhou等[6]确定了连通图的与顶点数及匹配数相关的最小 Kirchhoff指标.2010年,Feng等[7]给出了图的给定匹配数的Zagreb指标、Harary指标和超 Wiener指标的紧上(下)界,且确定了它们的极值图.2011年,Yu等[8]研究了给定围长的单圈图的离心率距离和,且刻画了最小和次最小离心率距离和的极值图.此外,他们还刻画了给定直径的一类树的最小和次最小离心率距离和的极值树.但是,对于图的给定匹配数的离心率距离和的极值图研究目前还没有结果.
本文解决了这个问题,给出了给定匹配数的离心率距离和的紧上界,且完全确定了其极值图.对离心率距离和的进一步研究具有一定的理论意义.文中未加述及的术语和符号参见文献[9].
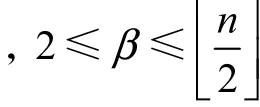
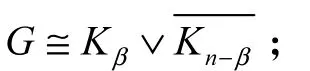

证明:令 G0是所有阶为n且匹配数为β的连通图中离心率距离和最小的图.由式(1)的 Tutte-Berge公式,存在顶点集 X0⊆ V(G0)使得为 方 便 起见,令X0=s且 o(G0- X0)=t,则n - 2β=t-s .
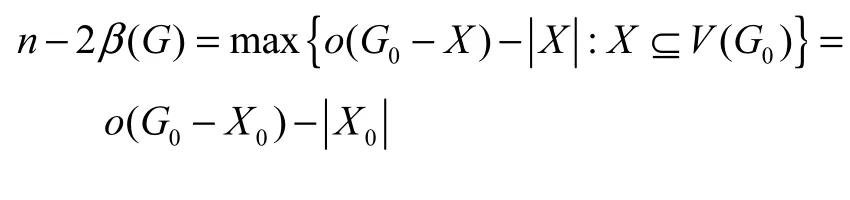

以下假设 s≥1,从而 t≥1.令 G1,G2,… ,Gt是G0- X0的所有奇分支.若 G0- X0有一个偶分支,则在 G0中通过添加一条连接 G0- X0的偶分支的一个顶点和奇分支的一个顶点的边,得到一个图,满足n -2β)≥o-X0)- X0= o(G0-X0)-X0.从而有β)= β,且由引理 1,Gˆ的离心率距离和比 G0小,矛盾.因此,G0- X0不含有任何偶分支.类似地,G1,G2,… ,Gt及由 X0导出的子图都是完全图,且G1,G2,… ,Gt中的任一顶点邻接于 X0的每一个顶点.令ni= V(Gi),i = 1,2,… ,t ,则
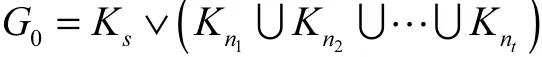
注意到,0G的直径是2,从而
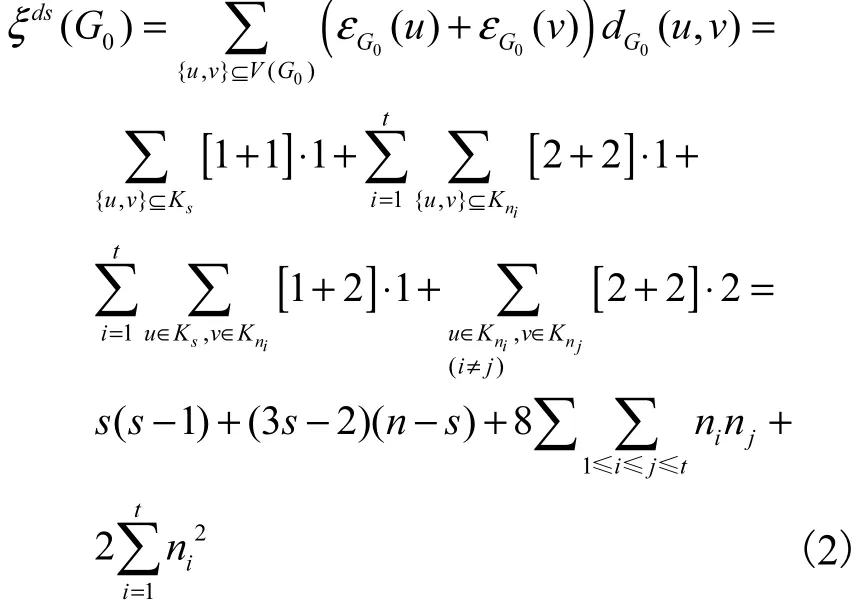
从而
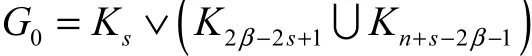
因此,式(2)可改写为
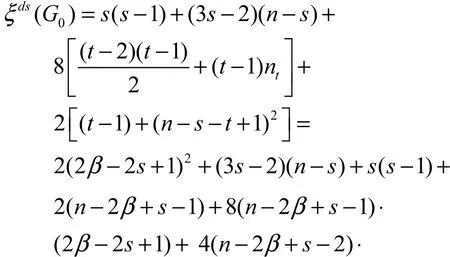


由于 β≥2,有 g(1)- g(β)=1-5 n - 10β2+9β + 5nβ .令b是二次方程 - 10β2+ (5 n + 9)β +1-5 n=0的一个较大的根,则

因此,若 β≤ b,则 g (1)≤ g(β);而当 β≥ b,则g (β)≤ g(1).证毕.
[1] Wiener H. Structural determination of paraffin boiling point[J]. Journal of the American Chemical Society,1947,69(1):17-20.
[2] Sharma V,Goswami R,Madan A K. Eccentric connectivity index:A novel highly discriminating topological descriptor for structure property and structure activity studies[J]. Journal of Chemical Information and Computer Science,1997,37(2):273-282.
[3] Gupta S,Singh M,Madan A K. Eccentric distance sum:A novel graph invariant for predicting biological and physical properties[J]. Journal of Mathmatical Analysis and Applications,2002,275(1):386-401.
[4] Lovász L,Plummer M D. Matching Theory[M]. Budapest:Akadémiai Kiadó,1986.
[5] Feng L H,Yu G H,Zhang X D. Spectral radius of graphs with given matching number[J]. Linear Algebra and its Applications,2007,422(1):133-138.
[6] Zhou B,Trinajstic N. The Kirchhoff index and the matching number[J]. International Journal of Quantum Chemistry,2009,109(13):2978-2981.
[7] Feng L H,Ilic A. Zagreb,Harary and hyper-Wiener indices of graphs with given matching number[J]. Applied Mathematics Letters,2010,23(8):943-948.
[8] Yu G H,Feng L H,Ilic A. On the eccentric distance sum of trees and unicyclic graphs[J]. Journal of Mathmatical Analysis and Applications,2011,375(1):99-107.
[9] Bondy J A,Murty U S R. Graph Theory with Applications[M]. London:Macmillan Press Ltd,1976.
图的给定匹配数的离心率距离和
安明强,孙明晶,刘寅立,孟祥波
Eccentric Distance Sum of Graphs with a Given Matching Number
AN Mingqiang,SUN Mingjing,LIU Yinli,MENG Xiangbo
(College of Science,Tianjin University of Science & Technology,Tianjin 300457,China)
Aimed at a novel graph invariant for predicting biological and physical properties named eccentric distance sum,by using the Tutte-Berge formula and the method of graph transformation,sharp lower bound for the eccentric distance sum of graphs with a given matching number,and the extremal graphs were successully determined.
eccentric distance sum;matching number;extremal graphs
O157.5 文献标志码:A 文章编号:1672-6510(2015)02-0075-03
10.13364/j.issn.1672-6510.20140072
2014-05-12;
2014-08-29
国家自然科学基金资助项目(11001197)
安明强(1982—),男,甘肃天水人,讲师,anmq@tust.edu.cn.
常涛
【科研成果简介】
